Типы статистических шкал
5.1.1 Типы статистических шкал
В эмпирическом исследовании могут встречаться, к примеру, следующие переменные (указано их наиболее вероятное кодирование):
|
Пол |
1 = мужской |
|
|
2 = женский |
|
Семейное положение |
1 = холост/не замужем |
|
|
2 = женат/замужем |
|
|
3 = вдовец/вдова |
|
|
4 = разведен(а) |
|
Курение |
1 = некурящий |
|
|
2 = изредка курящий |
|
|
3 = интенсивно курящий |
|
|
4 = очень интенсивно курящий |
|
Месячный доход |
1 = до 3000 DM |
|
|
2 = 3001 - 5000 DM |
|
Коэффициент интеллекта (I.Q.) |
3 = более 5000 DM |
|
Возраст, лет |
|
Рассмотрим сначала графу Пол. Мы видим, что назначение соответствия цифр 1 и 2 обоим полам абсолютно произвольно, их можно было поменять местами или обозначить другими цифрами
Мы, конечно, не имеем в виду, что женщины стоят на ступеньку ниже мужчин, или :о мужчины значат меньше, чем женщины. Следовательно, отдельным числам не соответствует никакою эмпирического значения. В этом случае говорят о переменных, относящихся к номинальной шкале. В нашем примере рассматривается переменная с номинальной шкалой, имеющая две категории. Такая переменная имеет еще одно название- дихотомическая.
Такая же ситуация и с переменной Семейное положение. Здесь также соответствие -:жду числами и категориями семейного положения не имеет никакого эмпирического значения. Но в отличии от Пола, эта переменная не является дихотомической — у нее четыре категории вместо двух. Возможности обработки переменных, относящихся к номинальной шкале очень ограничены. Собственно говоря, можно провести только частотный анализ таких переменных. К примеру, расчет среднего значения для переменной Семейное положение, совершенно бессмысленен. Переменные, относящиеся к номинальной шкале часто используются для группировки, с помощью которых совокупная выборка разбивается по категориям этих переменных. В частичных выборках проводятся одинаковые статистические тесты, результаты которых затем сравниваются друг с другом.
В качестве следующего примера рассмотрим переменную Курение. Здесь кодовым цифрам присваивается эмпирическое значение в том порядке, в котором они расположены в списке. Переменная Курение, в итоге, сортирована в порядке значимости снизу вверх: умеренный курильщик курит больше, нежели некурящий, а сильно курящий — больше, чем умеренный курильщик и т.д. Такие переменные, для которых используются численные значения, соответствующие постепенному изменению эмпирической значимости, относятся к порядковой шкале.
Однако эмпирическая значимость этих переменных не зависит от разницы между соседними численными значениями. Так, несмотря на то, что разница между значениями кодовых чисел для некурящего и изредка курящего и изредка курящего и интенсивно курящего в обоих случаях равна единице, нельзя утверждать, что фактическое различие между некурящим и изредка курящим и между изредка курящим и интенсивно курящим одинаково. Для этого данные понятия слишком расплывчаты.
К классическими примерами переменных с порядковой шкалой относятся также переменные, полученные в результате объединения величин в классы, как Месячный доход в нашем примере.
Кроме частотного анализа, переменные с порядковой шкалой допускают также вычисление определенных статистических характеристик, таких как медианы. В некоторых случаях возможно вычисление среднего значения. Если должна быть установлена связь (корреляция) с другими переменными такого рода, для этой цели можно использовать коэффициент ранговой корреляции.
Для сравнения различных выборок переменных, относящихся к порядковой шкале, могут применяться непараметрические тесты, формулы которых оперируют рангами.
Рассмотрим теперь коэффициент интеллекта (IQ). Не только его абсолютные значения отображают порядковое отношение между респондентами, но и разница между двумя значениями также имеет эмпирическую значимость. Например, если у Ганса IQ равен 80, у Фрица — 120 и у Отто — 160, можно сказать, что Фриц в сравнении с Гансом настолько же интеллектуальнее насколько Отто в сравнении с Фрицем (а именно — на 40 единиц IQ). Однако, основываясь только на том, что значение IQ у Ганса в два раза меньше, чем у Отто, исходя из определения IQ нельзя сделать вывод, что Отто вдвое умнее Ганса.
Такие переменные, у которых разность (интервал) между двумя значениями имеет эмпирическую значимость, относятся к интервальной шкале. Они могут обрабатываться любыми статистическим методами без ограничений. Так, к примеру, среднее значение является полноценным статистическим показателем для характеристики таких переменных.
Наконец, мы достигли наивысшей статистической шкалы, на которой эмпирическую значимость приобретает и отношение двух значений. Примером переменной, относящейся к такой шкале является возраст: если Максу 30 лет, а Морицу 60, можно сказать, что Мориц вдвое старше Макса. Шкала, к которой относятся данные называется шкалой отношений. К этой шкале относятся все интервальные переменные, которые имеют абсолютную нулевую точку. Поэтому переменные относящиеся к интервальной шкале, как правило, имеют и шкалу отношений.
Подводя итоги, можно сказать, что существует четыре вида статистических шкал, на которых могут сравниваться численные значения:
|
Статистическая шкала |
Эмпирическая значимость |
|
Номинальная |
Нет |
|
Порядковая |
Порядок чисел |
|
Интервальная |
Разность чисел |
|
Шкала отношений |
Отношение чисел |
На практике, в том числе в SPSS, различие между переменными, относящимися к интервальной шкале и шкале отношений обычно несущественно. То есть в дальнейшем практически всегда речь будет идти о переменных, относящихся к интервальной шкале.
Пользователь SPSS должен четко разбираться в видах статистических шкал и при выборе метода обращать внимание на то, чтобы были определены надлежащие виды шкал.
Мы уже указывали, что переменные, относящиеся к номинальной шкале допускают весьма ограниченные возможности для проведения анализа. Исключение в некоторых ситуациях составляют дихотомические переменные. Для них можно, по крайней мере, определять ранговую корреляцию. Если, например, обнаруживается корреляция коэффициента интеллекта с полом, то положительный коэффициент корреляции означает, что женщины интеллектуальнее, чем мужчины. Однако если переменные, относящиеся к номинальной шкале не являются дихотомическими, вычисление коэффициентов ранговой корреляции не имеет смысла.
Нормальное распределение
5.1.2 Нормальное распределение
Многочисленные методы, с помощью которых обрабатываются переменные, относящиеся к интервальной шкале, исходят из гипотезы, что их значения подчиняются нормальному распределению. При таком распределении большая часть значений группируется около некоторого среднего значения, по обе стороны от которого частота наблюдений равномерно снижается.
В качестве примера рассмотрим нормальное распределение возраста, которое строится по данным исследований гипертонии (файл hyper.sav) с помощью команд меню Graphs (Графы) Histogramm... (Гистограмма) (см. рис. 5.1).
На диаграмме нанесена кривая нормального распределения (Колокол Гаусса). Реальное распределение в большей или меньшей степени отклоняется от этой идеальной кривой. Выборки, строго подчиняющиеся нормальному распределению, на практике, как правило, не встречаются. Поэтому почти всегда необходимо выяснить, можно ли реальное распределение считать нормальным и насколько значительно заданное распределение отличается от нормального.
Перед применением любого метода, который предполагает существование нормального распределения, наличие последнего нужно проверять в первую очередь. Классическим примером статистического теста, который исходит из гипотезы о нормальном распределении, можно назвать t-тест Стьюдента, с помощью которого сравнивают две независимые выборки. Если же данные не подчиняются нормальному распределению, следует использовать соответствующий непараметрический тест, в случае двух независимых выборок — U-тест Манна и Уитни.
Если визуальное сравнение реальной гистограммы с кривой нормального распределения кажется недостаточным, можно применить тест Колмогорова-Смирнова, который находится в меню Analyze (анализ данных) в наборе непараметрических тестов (см. раздел 14.5).
Зависимость и независимость выборок
5.1.3 Зависимость и независимость выборок
Две выборки зависят друг от друга, если каждому значению одной выборки можно закономерным и однозначным способом поставить в соответствие ровно одно значение другой выборки. Аналогично определяется зависимость нескольких выборок.
Чаще всего зависимые выборки возникают, когда измерение проводится для нескольких моментов времени. Зависимые выборки образуют значения параметров изучаемого процесса, соответствующие различным моментам времени.
В SPSS зависимые (также связанные, спаренные) выборки будут представляться разными переменными, которые сопоставляются друг с другом в соответствующем тесте на одной и той же совокупности наблюдений.
Если закономерное и однозначное соответствие между выборками невозможно, эти выборки являются независимыми. В SPSS независимые выборки содержат разные наблюдения (например, относящиеся к различным респондентам), которые обычно различаются с помощью групповой переменной, относящейся к номинальной шкале.
Предварительные условия для проведения статистического теста
5.1 Предварительные условия для проведения статистического теста
В большинстве случаев перед применением статистического теста ставится вопрос: каков характер заданных условий? В частности, необходимо выяснить следующие моменты:
К какой статистической шкале относится данная переменная?
Если речь идёт о переменных с интервальной шкалой, то подчиняются ли они закону нормального распределения?
Являются ли сравниваемые выборки зависимыми или независимыми?
Обзор распространенных тестов для проверки гипотез о среднем
5.2 Обзор распространенных тестов для проверки гипотез о среднем
В наиболее распространенной ситуации, когда требуется сравнить друг с другом разные выборки по их средних значениям или медианам, с учетом условий, описанных в разделе 5.1, обычно применяется один из восьми следующих тестов.
Переменные, относящиеся к интервальной шкале и подчиняющиеся нормальному распределению
|
Количество сравниваемых выборок |
Зависимость |
Тест |
|
1 |
Независимые |
t-тест Стьюдента |
|
1 |
Зависимые |
t-тест для зависимых выборок |
|
>2 |
Независимые |
Простой дисперсионный анализ |
|
>2 |
Зависимые |
Простой дисперсионный анализ с повторными измерениями |
Переменные, относящиеся к порядковой шкале или переменные, относящиеся к интервальной шкале, но не подчиняющиеся нормальному распределению
|
Количество сравниваемых выборок |
Зависимость |
Гест |
|
1 |
Независимые |
U-тест Манна и Уитни |
|
2 |
Зависимые |
тест Уилкоксона |
|
>2 |
Независимые |
Н-тест Крускала и Уоллиса |
|
>2 |
Зависимые |
тест Фридмана |
Для каждой из этих двух групп тестов в SPSS имеются отдельные пункты меню, а именно Analyze (Анализ) Compare Means (Сравнение средних) или Analyze (Анализ) Nonparametric Tests (Непараметрические тесты)
Исключение составляет простой дисперсионный анализ с повторными измерениями. Этот метод нельзя найти в разделе Compare Means. Он вызывается командой меню General Linear Model (Общая линейная модель).
Вероятность ошибки р
5.3 Вероятность ошибки р
Если следовать подразделению статистики на описательную и аналитическую, то задача аналитической статистики - предоставить методы, с помощью которых можно было бы объективно выяснить, например, является ли наблюдаемая разница в средних значениях или взаимосвязь (корреляция) выборок случайной или нет.
Например, если сравниваются два средних значения выборок, то можно сформулировать две предварительных гипотезы:
Гипотеза 0 (нулевая): Наблюдаемые различия между средними значениями выборок находятся в пределах случайных отклонений.
Гипотеза 1 (альтернативная): Наблюдаемые различия между средними значениями нельзя объяснить случайными отклонениями.
В аналитической статистике разработаны методы вычисления так называемых тестовых (контрольных) величин, которые рассчитываются по определенным формулам на основе данных, содержащихся в выборках или полученных из них характеристик. Эти тестовые величины соответствуют определенным теоретическим распределениям (t-pacnpe-лелению, F-распределению, распределению X2 и т.д.), которые позволяют вычислить так называемую вероятность ошибки. Это вероятность равна проценту ошибки, которую можно допустить отвергнув нулевую гипотезу и приняв альтернативную.
Вероятность определяется в математике, как величина, находящаяся в диапазоне от 0 до 1. В практической статистике она также часто выражаются в процентах. Обычно вероятность обозначаются буквой р:
0<р< 1
Вероятности ошибки, при которой допустимо отвергнуть нулевую гипотезу и принять альтернативную гипотезу, зависит от каждого конкретного случая. В значительной степени эта вероятность определяется характером исследуемой ситуации. Чем больше требуемая вероятность, с которой надо избежать ошибочного решения, тем более узкими выбираются границы вероятности ошибки, при которой отвергается нулевая гипотеза, так называемый доверительный интервал вероятности.
Существует общепринятая терминология, которая относится к доверительным интервалам вероятности. Высказывания, имеющие вероятность ошибки р <= 0,05. называются значимыми; высказывания с вероятностью ошибки р <= 0,01 - очень значимыми, а высказывания с вероятностью ошибки р <= 0,001 - максимально значимыми. В литературе такие ситуации обозначают одной, двумя или тремя звездочками.
|
Вероятность ошибки |
Значимость |
Обозначение |
|
р > 0.05 |
Не значимая |
ns |
|
р <= 0.05 |
Значимая |
* |
|
р <= 0.01 |
Очень значимая |
** |
|
р <= 0.001 |
Максимально значимая |
*** |
В SPSS вероятность ошибки р имеет различные обозначения; звездочки для указания степени значимости применяются лишь в немногих случаях.
Времена, когда не было компьютеров, пригодных для статистического анализа, давали практикам по крайней мере одно преимущество.: Так как все вычисления надо было выполнять вручную, статистик должен был сначала тщательно обдумать, какие вопросы можно решить с помощью того или иного теста. Кроме того, особое значение придавалось точной формулировке нулевой гипотезы.
Нос помощью компьютера и такой мощной программы, как SPSS, очень легко можно провести множество тестов за очень короткое время. К примеру, если в таблицу сопряженности свести 50 переменных с другими 20 переменными и выполнить тест %2, то получится 1000 результатов проверки значимости или 1000 значений р. Некритический подбор значимых величин может дать бессмысленный результат, так как уже при граничном уровне значимости р = 0,05 в пяти процентах наблюдений, то есть в 50 возможных наблюдениях, можно ожидать значимые результаты.
Этим ошибкам первого рода (когда нулевая гипотеза отвергается, хотя она верна) следует уделять достаточно внимания. Ошибкой второго рода называется ситуация, когда нулевая гипотеза принимается, хотя она ложна. Вероятность допустить ошибку первого рода равна вероятности ошибки р. Вероятность ошибки второго рода тем меньше, чем больше вероятность ошибки р.
Структурирование, ввод и проверка данных
5.4.1 Структурирование, ввод и проверка данных
Прежде чем мы сможем применить статистические методы или строить графики, естественно, следует представить собранные данные в форме, пригодной для обработки. При этом рекомендуется придерживаться следующего плана действий:
Проведите структурирование набора данных; прежде всего выясните, к какими категориям относятся Ваши наблюдения и к каким — переменные. В большинстве случаев это ясно сразу. Если структурирование провести не удается, SPSS применять нельзя, да и все остальные статистические программы также требуют, чтобы данные были структурированы. Подробнее об этом см. раздел 3.2.
Определите шкалу, к которой относятся переменные (см. раздел 5.1.1).
Составьте кодировочную таблицу (см. раздел 3.1).
Введите данные в Редакторе данных (см. раздел 3.4), учитывая кодировочную таблицу. Если для ввода данных вы хотите использовать другие программы (например, Excel, dBase), это вполне допустимо; SPSS может работать с файлами данных этих программ. Не вводите данные, которые можно вычислить на основе других данных. Эти вычисления следует предоставить компьютеру (см. главу 8). Если данные уже были введены в других программах статистики (например, SAS, Stata. Statistica), их можно преобразовать в файлы SPSS с помощью таких утилит, как, к примеру, DBMS/COPY.
Проверьте введенные данные на отсутствие ошибок и осмысленность. Подробнее об этом см. раздел 10.1.
Установите, подчиняются ли нормальному распределению переменные, относящиеся к интервальной шкале (см. раздел 5.1.2).
Теперь можно начинать статистическую обработку введенных данных. Учтите, что анализ может быть выполнен только для наблюдений, сгруппированных определенным образом см. главу 7). Об основных принципах работы с версией 9 можно прочесть в главе 4.
Описательный (дескриптивный) анализ
5.4.2 Описательный (дескриптивный) анализ
Этот вид анализа включает описательное представление отдельных переменных. К нему относятся создание частотной таблицы, вычисление статистических характеристик или графическое представление. Частотные таблицы строятся для переменных, относящихся к номинальной шкале и для порядковых переменных, имеющих не слишком много категорий; об этом см. главы 6, 12 и 24.
Для переменных относящихся к номинальной шкале нельзя вычислить никаких значимых статистических характеристик. Наиболее часто для порядковых переменных и переменных, относящихся к интервальной шкале, но не подчиняющихся нормальному распределению, вычисляются медианы и оба квартиля (см. раздел 6.2); при небольшом числе категорий можно использовать вариант для концентрированных данных см. раздел 6.3).
Для переменных, относящихся к интервальной шкале и подчиняющихся нормальному распределению, чаще всего вычисляется среднее значение и стандартное отклонение пли стандартная ошибка (см. раздел 6.2). Однако следует выбрать только одну из этих двух характеристик разброса. Для переменных, относящихся ко всем статистическим шкалам, можно построить большое разнообразных графиков, на которых представлены частоты, средние значения или другие характеристики. Подробнее об этом в главах 22 и 23.
Аналитическая статистика
5.4.3 Аналитическая статистика
Практически любой статистический анализ наряду с чисто описательными операциями включает те или иные аналитические методы (тесты значимости), при применении которых в конечном счете определяется вероятности ошибки р (см. раздел 5.3).
Большая группа тестов служит для выяснения того, различаются ли две или более различных выборки по своим средним значениям или медианам. При этом учитывается разница между независимыми выборками (разные наблюдения) и зависимыми выборками (разные переменные; см. раздел 5.1.3). В зависимости количества выборок (две или более), от того, зависимы ли выборки или нет, относятся ли переменные к интервальной или порядковой шкале, подчиняются ли нормальному распределению — применяются специализированные тесты (см. раздел 5.2).
Очень часто встречается ситуация, когда сравниваются различные группы наблюдений или значений переменных, относящихся к номинальной шкале. В этом случае строятся таблицы сопряженности (см. главу 11). Другая группа тестов касается исследования связей между двумя переменными, то есть выявления корреляций и восстановления регрессий (см. главу 15, раздел 16.1).
Кроме этих довольно простых статистических методов существуют также более сложные методы многомерного анализа, в которых обычно одновременно используется очень много переменных. К примеру, если требуется свести большое количество переменных к меньшему количеству "пучков переменных", называемых факторами, то проводится факторный анализ (глава 19). Если же наша цель, противоположна — объединить заданные наблюдения, образовав из них кластеры, то применяется кластерный анализ (глава 20).
В определенной группе многомерных тестов вводится различие между зависимой переменной, называемой также целевой и несколькими независимыми переменными (переменными влияния или прогнозирования).
|
Зависимая переменная |
Независимые переменные |
Многомерный метол |
|
Дихотомическая |
Любые |
Двоичная логистическая регрессия (раздел 16.4); дискриминантный анализ (глава 18) |
|
Дихотомическая |
С номинальной или порядковой шкалой |
Логит-логарифмические линейные модели |
|
С номинальной шкалой |
С номинальной или порядковой шкалой |
Мультиномиальная логистическая регрессия (раздел 16.5) |
|
С порядковой шкалой |
С номинальной или порядковой шкалой |
Порядковая регрессия (раздел 16.6) |
|
С интервальной шкалой |
С номинальной или порядковой шкалой |
Дисперсионный анализ (раздел 17.1) |
|
С интервальной шкалой |
Любые |
Ковариационный анализ (раздел 17.2); множественный регрессионный анализ (раздел 16.2) |
При мультиномиальной логистической регрессии и порядковой регрессии могут также использоваться ковариации, относящиеся к интервальной шкале.
Независимые переменные, относящиеся к номинальной шкале, при двоичной логистической регрессии, дискриминантном анализе и многозначном регрессионном анализе должны быть дихотомическими либо раскладываться на набор дихотомических переменных (см. раздел 16.2). Логит-логарифмические линейные модели рассматриваются не в этой книге, а во втором томе, посвященном методам исследования рынка и общественного мнения.
Кроме упомянутых здесь, существует еще несколько методов анализа, например, пробит-анализ или анализ надежности; об их назначении можно узнать из соответствующих глав.
Обзор статистических методов
5.4 Обзор статистических методов
В этом разделе мы попытаемся составить небольшой путеводитель по данной книге, дав обзор последовательности действий, которые выполняются при статистическом анализе.
Основы статистики
Глава 5. Основы статистики
Основы статистики 5.1 Предварительные условия для проведения статистического теста 5.1.1 Типы статистических шкал 5.1.2 Нормальное распределение 5.1.3 Зависимость и независимость выборок 5.2 Обзор распространенных тестов для проверки гипотез о среднем 5.3 Вероятность ошибки р 5.4 Обзор статистических методов 5.4.1 Структурирование, вводи проверка данных 5.4.2 Описательный (дескриптивный) анализ 5.4.3 Аналитическая статистикаОсновы статистики
Основы статистики
Овладение приемами работы с такой программой, как SPSS требует предварительных познаний в области статистики. Здесь мы коротко остановимся на некоторых основных понятиях, с которыми непременно должен быть знаком пользователь, если он хочет использовать SPSS. В первую очередь сюда относятся предварительные оценки, которые выполняются перед проведением любого статистического теста: классификация переменных по статистическим шкалам, проверка наличия нормального распределения и выделение независимых и зависимых выборок. В следующих разделах представлено описание наиболее часто проводимой процедуры проверки гипотезы о среднем значении и рассматривается значение вероятности ошибки р. Завершает главу обзор методов статистической обработки с указанием глав, в которых они будут рассматриваться в этой книге.
Распределение возраста
Распределение возраста
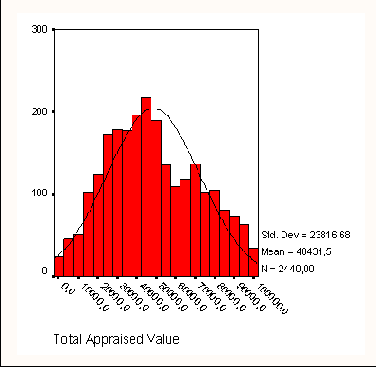
В нашем примере с распределением возрастов тест Колмогорова-Смирнова не показывает значительного отклонения от нормального распределения.
Еще одну возможность проверки наличия нормального распределения дает построение графика нормального распределения (см. разделы 10.4.1, 22.12), в котором наблюдаемые значения сопоставляются с ожидаемыми при нормальном распределении.
