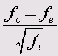Создание таблиц сопряженности
11.1 Создание таблиц сопряженности
Загрузите файл studium.sav.
Для создания таблиц сопряженности и вычисления меры связанности на их основе, выберите в меню команды Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Crosstabs... (Таблицы сопряженности) Откроется диалоговое окно Crosstabs (см. рис. 11.1).
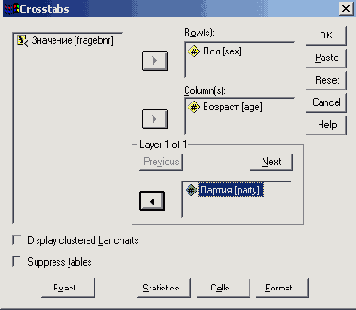
Список исходных переменных содержит переменные открытого файла данных. Здесь можно выбрать переменные для строк и столбцов таблицы сопряженности. Для каждого сочетания двух переменных будет создана таблица сопряженности. Например, если в списке строк (Rows) находится три переменных, а в списке столбцов (Columns) — две, то мы получим 3*2 = 6 таблиц сопряженности. Сначала мы построим таблицу сопряженности из переменных sex (пол) и psyche (психическое состояние). Поступите следующим образом:
Перенесите переменную sex в список строк, а переменную psyche — в список столбцов.
Графическое представление таблиц сопряженности
11.2 Графическое представление таблиц сопряженности
Чтобы сделать более наглядными данные, содержащиеся в таблицах сопряженности, их можно представить визуально. Для этого поступите следующим образом:
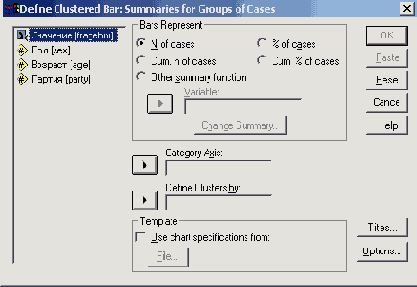
Выберите в меню команды Graphs (Графики) Ваr... (Столбчатые) Откроется диалоговое окно Bar Charts (Столбчатые диаграммы).
Выберите пункт Clustered (Группированные), оставьте предлагаемую по умолчанию опцию Summaries for groups of cases (Сводка категорий переменной) и щелкните на кнопке Define (Определить). Откроется диалоговое окно Define Clustered Bar: Summaries for groups of cases (Определить столбчатую диаграмму: Сводка категорий переменной).
Выберите пункт % of cases (% наблюдений).
Перенесите переменную psyche в поле Category Axis (Ось категорий), а переменную sex — в поле Define Clusters by (Определить группы по).
Щелкните на кнопке Titles... (Заголовки). Откроется диалоговое окно Titles (см. рис. 11.6).
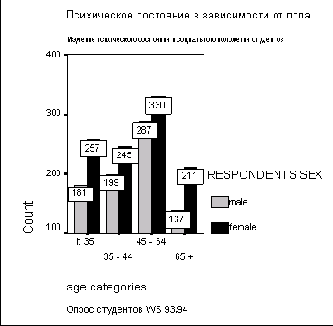
В поле Line 1 (Строка 1) введите заголовок "Психическое состояние в зависимости от пола", в поле Subtitle — подзаголовок "Изучение психического состояния и социального положения студентов", а в поле Footnote, Line 1 (Нижний колонтитул, строка 1) — текст "Опрос студентов WS 93/94". Подтвердите ввод кнопкой Continue.
Щелкните на кнопке Options... (Параметры). Откроется диалоговое окно Options.
Тест хи-квадрат (X2)
11.3.1 Тест хи-квадрат (X2)
При проведении теста хи-квадрат проверяется взаимная независимость двух переменных таблицы сопряженности и благодаря этому косвенно выясняется зависимость обоих переменных. Две переменные считаются взаимно независимыми, если наблюдаемые частоты (f0) в ячейках совпадают с ожидаемыми частотами (fe).
Для того, чтобы провести тест хи-квадрат с помощью SPSS, выполните следующие действия:
Выберите в меню команды Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Crosstabs... (Таблицы сопряженности)
Кнопкой Reset (Сброс) удалите возможные настройки.
Перенесите переменную sex в список строк, а переменную psyche — в список столбцов.
Щелкните на кнопке Cells... (Ячейки). В диалоговом окне установите, кроме предлагаемого по умолчанию флажка Observed, еще флажки Expected и Standardized. Подтвердите выбор кнопкой Continue.
Щелкните на кнопке Statistics... (Статистика).
Откроется описанное выше диалоговое окно Crosstabs: Statistics.
Установите флажок Chi-square (Хи-квадрат). Щелкните на кнопке Continue, а в главном диалоговом окне — на ОК.
Вы получите следующую таблицу сопряженности.
Пол * Психическое состояние Таблица сопряженности
|
Психическое состояние |
Total | ||||||
|
|
|
| Крайне неустой-чивое |
Неустой-чивое |
Устой-чивое | Очень устойчивое | |
|
Пол |
женский |
Count | 16 |
18 |
9 |
1 |
44 |
|
Expected Count | 7,9 |
16,6 |
17,0 |
2,5 |
44,0 | ||
|
Std. Residual | 2,9 |
,3 |
-1,9 |
-.9 |
| ||
|
Мужской |
Count | 3 |
22 |
32 |
5 |
62 | |
|
Expected Count | 11,1 |
23,4 |
24,0 |
3,5 |
62,0 | ||
|
Std. Residual | -2,4 |
-,3 |
1,6 |
,8 |
| ||
|
Total |
|
Count | 19 |
40 |
41 |
6 |
106 |
|
Expected Count | 19,0 |
40,0 |
41,0 |
6,0 |
106,0 | ||
Кроме того, в окне просмотра будут показаны результаты теста хи-квадрат:
Chi-Square Tests (Тесты хи-квадрат)
|
|
Value (Значение) |
df |
Asymp. Sig. (2-sided) (Асимптотическая значимость (двусторонняя)) |
|
Pearson Chi-Square (Хи-квадрат по Пирсону) |
22,455 (а) |
3 |
,000 |
|
Likelihood Ratio (Отношение правдоподобия) |
23,688 |
3 |
,000 |
|
Linear-by-Linear Association (Зависимость линейный-линейный) |
20,391 |
1 |
,000 |
|
N of Valid Cases (Кол-во допустимых случаев) |
106 |
|
|
а. 2 cells (25,0%) have expected count less than 5. The minimum expected count is 2,49 (2 ячейки (25%) имеют ожидаемую частоту менее 5. Минимальная ожидаемая частота 2,49.)
Для вычисления критерия хи-квадрат применяются три различных подхода: формула Пирсона, поправка на правдоподобие и тест Мантеля-Хэнзеля. Если таблица сопряженности имеет четыре поля и ожидаемая вероятность менее 5, дополнительно выполняется точный тест Фишера.
Критерий хи-квадрат по Пирсону
Обычно для вычисления критерия хи-квадрат используется формула Пирсона:
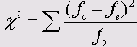
Здесь вычисляется сумма квадратов стандартизованных остатков по всем полям таблицы сопряженности. Поэтому поля с более высоким стандартизованным остатком вносят более весомый вклад в численное значение критерия хи-квадрат и, следовательно, — в значимый результат. Согласно правилу, приведенному в разделе 8.7.2, стандартизованный остаток 2 или более указывает на значимое расхождение между наблюдаемой и ожидаемой частотами.
В рассматриваемом нами примере формула Пирсона дает максимально значимую величину критерия хи-квадрат (р<0,001). Если рассмотреть стандартизованные остатки в отдельных полях таблицы сопряженности, то на основе вышеприведенного правила можно сделать вывод, что эта значимость в основном определяется полями, в которых переменная psyche имеет значение "крайне неустойчивое". У женщин это значение сильно повышено, а у мужчин — понижено.
Корректность проведения теста хи-квадрат определяется двумя условиями: во-первых, ожидаемые частоты < 5 должны встречаться не более чем в 20 % полей таблицы; во-вторых, суммы по строкам и столбцам всегда должны быть больше нуля.
Однако в рассматриваемом примере это условие выполняется не полностью. Как указывает примечание после таблицы теста хи-квадрат, 25 % полей имеют ожидаемую частоту менее 5. Однако, так как допустимый предел4в 20 % превышен лишь ненамного и эти поля, вследствие своего очень малого стандартизованного остатка, вносят весьма незначительную долю в величину критерия хи-квадрат, это нарушение можно считать несущественным.
Критерий хи-квадрат с поправкой на правдоподобие
Альтернативой формуле Пирсона для вычисления критерия хи-квадрат является поправка на правдоподобие:
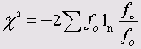
При большом объеме выборки формула Пирсона и подправленная формула дают очень близкие результаты. В нашем примере критерий хи-квадрат с поправкой на правдоподобие составляет 23,688.
Тест Мантеля-Хэнзеля
Дополнительно в таблице сопряженности под обозначением linear-by-linear ("линейный-по-линейному") выводится значение теста Мантеля-Хэнзеля (20,391). Эта форма критерия хи-квадрат с поправкой Мантеля-Хэнзеля — еще одна мера линейной зависимости между строками и столбцами таблицы сопряженности. Она определяется как произведение коэффициента корреляции Пирсона на количество наблюдений, уменьшенное на единицу:

Полученный таким образом критерий имеет одну степень свободы. Метод Мантеля-Хэнзеля используется всегда, когда в диалоговом окне Crosstabs: Statistics установлен флажок Chi-square. Однако для данных, относящихся к с номинальной шкале, этот критерий неприменим.
Коэффициенты корреляции
11.3.2 Коэффициенты корреляции
До сих пор мы выясняли лишь сам факт существования статистической зависимости между двумя признаками. Далее мы попробуем выяснить, какие заключения можно сделать о силе или слабости этой зависимости, а также о ее виде и направленности. Критерии количественной оценки зависимости между переменными называются коэффициентами корреляции или мерами связанности. Две переменные коррелируют между собой положительно, если между ними существует прямое, однонаправленное соотношение. При однонаправленном соотношении малые значения одной переменной соответствуют малым значениям другой переменной, большие значения — большим. Две переменные коррелируют между собой отрицательно, если между ними существует обратное, разнонаправленное соотношение. При разнонаправленном соотношении малые значения одной переменной соответствуют большим значениям другой переменной и наоборот. Значения коэффициентов корреляции всегда лежат в диапазоне от -1 до +1.
В качестве коэффициента корреляции между переменными, принадлежащими порядковой шкале применяется коэффициент Спирмена, а для переменных, принадлежащих к интервальной шкале — коэффициент корреляции Пирсона (момент произведений). При этом следует учесть, что каждую дихотомическую переменную, то есть переменную, принадлежащую к номинальной шкале и имеющую две категории, можно рассматривать как порядковую.
Для начала мы проверим существует ли корреляция между переменными sex и psyche из файла studium.sav. При этом мы учтем, что дихотомическую переменную sex можно считать порядковой. Выполните следующие действия:
Выберите в меню команды Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Crosstabs... (Таблицы сопряженности)
Перенесите переменную sex в список строк, а переменную psyche — в список столбцов.
Щелкните на кнопке Statistics... (Статистика). В диалоге Crosstabs: Statistics установите флажок Correlations (Корреляции). Подтвердите выбор кнопкой Continue.
В диалоге Crosstabs откажитесь от вывода таблиц, установив флажок Supress tables (Подавлять таблицы). Щелкните на кнопке ОК.
Будут вычислены коэффициенты корреляции Спирмена и Пирсона, а также проведена проверка их значимости:
Symmetric Measures (Симметричные меры)
|
Value (Значение) |
Asympt. Std. Error (а) Асимпто-тическая стандарт-ная ошибка) |
Approx. Т (b) (Приблиз. Т) |
Approx. Sig. (Приблизи- тельная значи-мость) | ||
|
Interval by Interval (Интерваль- ный-интерваль- ныи) |
Pearson's R (R Пирсона) |
,441 |
,081 |
5,006 |
,000 (с) |
|
Ordinal by Ordinal (Порядковый-порядковый) |
Spearman Correlation (Корреляци я по Спирмену) |
.439 |
,083 |
4,987 |
,000 (с) |
|
N of Valid Cases (Кол-во допустимых случаев) |
|
106 |
|
|
|
a. Not assuming the null hypothesis (Нулевая гипотеза не принимается).
b. Using the asymptotic standard error assuming the null hypothesis (Используется асимптотическая стандартная ошибка с принятием нулевой гипотезы).
с. Based on normal approximation (На основе нормальной аппроксимации).
Так как здесь нет переменных с интервальной шкалой, мы рассмотрим коэффициент корреляции Спирмена. Он составляет 0,439 и является максимально значимым (р<0,001).
Для словесного описания величин коэффициента корреляции применяется следующая таблица:
|
Значение коэффициента корреляции r |
Интерпретация |
|
0 < г <= 0,2 0,2 < г <= 0,5 0,5 < г <= 0,7 0,7 < г <= 0,9 0,9 < г <= 1 |
Очень слабая корреляция Слабая корреляция Средняя корреляция Сильная корреляция Очень сильная корреляция |
Исходя из вышеприведенной таблицы, можно сделать следующие заключения: Между переменными sex и psyche существует слабая корреляция (заключение о силе зависимости), переменные коррелируют положительно (заключение о направлении зависимости).
В переменной psyche меньшие значения соответствуют отрицательному психическому состоянию, а большие — положительному. В переменной sex, в свою очередь, значение "1" соответствует женскому полу, а "2" — мужскому.
Следовательно, однонаправленность соотношения можно интерпретировать следующим образом: студентки оценивают свое психическое состояние более негативно, чем '.х коллеги-мужчины или, что вероятнее всего, в большей степени склонны согласиться на такую оценку при проведении анкетирования. Строя подобные интерпретации, нужно учитывать, что корреляция между двумя признаками не обязательно равнозначна их Функциональной или причинной зависимости. Подробнее об этом см. в разделе 15.3.
Теперь проверим корреляцию между переменными alter и semester. Применим методику, описанную выше. Мы получим следующие коэффициенты:
Symmetric Measures
|
Value |
Asympt. Std. Error (a) |
Approx. Т (b) |
Approx. Sig. | ||
|
Interval by Interval |
Pearson's R |
,807 |
,041 |
13,930 |
,000 (c) |
|
Ordinal by Ordinal |
Spearman Correlation |
,743 |
,060 |
11,310 |
,000 (c) |
|
N of Valid Cases |
106 |
|
|
| |
a. Not assuming the null hypothesis (Нулевая гипотеза не принимается).
э. Using the asymptotic standard error assuming the null hypothesis (Используется асимптотическая стандартная ошибка с принятием нулевой гипотезы).
с. Based on normal approximation (На основе нормальной аппроксимации).
Так как переменные alter и semester являются метрическими, мы рассмотрим коэффициент Пирсона (момент произведений). Он составляет 0,807. Между переменными alter и semester существует сильная корреляция. Переменные коррелируют положительно. Следовательно, старшие по возрасту студенты учатся на старших курсах, что, собственно, не является неожиданным выводом.
Проверим на корреляцию переменные sozial (оценку социального положения) и psyche. Мы получим следующие коэффициенты:
Symmetric Measures
|
Value |
Asympt. Std. Error (a) |
Approx. Т (b) |
Approx. Sig. | ||
|
Interval by Interval |
Pearson's R |
-,688 |
,057 |
-9,703 |
,000 (c) |
|
Ordinal by Ordinal |
Spearman Correlation |
-,703 |
,059 |
-10,123 |
,000 (c) |
|
N of Valid Cases |
107 |
|
|
| |
a. Not assuming the null hypothesis (Нулевая гипотеза не принимается).
b. Using the asymptotic standard error assuming the null hypothesis (Используется асимптотическая стандартная ошибка с принятием нулевой гипотезы).
с. Based on normal approximation (На основе нормальной аппроксимации).
В этом случае мы рассмотрим коэффициент корреляции Спирмена; он составляет -0,703. Между переменными sozial и psyche существует средняя или сильная корреляция (граничное значение 0,7). Переменные коррелируют отрицательно, то есть чем больше значения первой переменной, тем меньше значения второй и наоборот. Так как малые значения переменной sozial характеризуют позитивное состояние (1 = очень хорошее, 2 = хорошее), а большие значения psyche — отрицательное состояние (1 = крайне неустойчивое, 2 = неустойчивое), следовательно, психологические затруднения во многом обусловлены социальными проблемами.
Меры связанности для переменных с номинальной шкалой
11.3.3 Меры связанности для переменных с номинальной шкалой
Коэффициент корреляции нельзя применять в качестве характеристики зависимости между переменными, если эти переменные принадлежат к номинальной шкале и имеют более двух категорий, потому что между их кодировками невозможно установить порядкового отношения и, следовательно, они не могут быть расположены в определенном, рационально объяснимом порядке.
Наилучшим средством для анализа таких зависимостей считается представленный в разделе 11.3.1 тест хи-квадрат, после которого при необходимости можно провести анализ наблюдаемых и ожидаемых частот, а также нормированных остатков. Этот анализ был описан в разделе 8.7.2.
Тем не менее и в этом случае также производились попытки разработать критерии количественной оценки степени связанности двух переменных, поставленных во взаимное соответствие. Эти критерии показывают степень взаимной зависимости или независимости двух переменных, принадлежащих к с номинальной шкале, причем значение 0 соответствует полной независимости переменных, а 1 — их максимальной зависимости. Меры связанности не могут иметь отрицательных значений, так как при отсутствии порядкового отношения нельзя дать ответа на вопрос о направлении зависимости.
В опросе членов городской организации одной из политических партий среди прочего выяснялось их занятие и определялось, выполняет ли респондент какую-либо партийную функцию. Выдержка из ответов респондентов-мужчин содержится в файле partei.sav.
Загрузите файл partei.sav и создайте таблицу сопряженности с переменной funk в строках и переменной beruf в столбцах.
Задайте вывод ожидаемых частот, стандартизованных остатков, процентов по столбцам и критерия хи-квадрат.
Занятие * Партийная работа Crosstabulation (Таблица сопряженности)
|
Занятие |
Total | ||||||
|
|
|
| Наемный работник |
Государст- венный служащий | Предпри-ниматель | ||
|
Партийная работа |
да |
Count | 13 |
16 |
7 |
36 | |
|
Expected Count | 12,4 |
10,1 |
13,5 |
36,0 | |||
|
% от Занятие | 59,1% |
88,9% |
29,2% |
56,3% | |||
|
Std. Residual | ,2 |
1,8 |
-1,8 |
| |||
|
нет |
Count | 9 |
2 |
17 |
28 | ||
|
Expected Count | 9,6 |
7,9 |
10,5 |
28,0 | |||
|
% от Занятие | 40,9% |
11,1% |
70.8% |
43,8% | |||
|
Std. Residual | -,2 |
-2,1 |
2,0 |
| |||
|
Total |
Count | 22 |
18 |
24 |
64 | ||
|
Expected Count | 22,0 |
18,0 |
24,0 |
64,0 | |||
|
% от Занятие | 100,0% |
100,0% |
100,0% |
100,0% | |||
Chi-Square Tests
|
|
Value |
df |
Asymp. Sig. (2-sided) |
|
Pearson Chi-Square (Критерий хи-квадрат по Пирсону) |
15,01 7 (a) |
2 |
,001 |
|
Likelihood Ratio (Отношение правдоподобия) |
16,421 |
2 |
,000 |
|
Li near-by-Li near Association (Зависимость линейный-линейный) |
4,420 |
1 |
,036 |
|
N of Valid Cases |
64 |
|
|
а. и cells (,0%) have expected count less than 5. The minimum expected count is 11,50. (0 ячеек (,0%) имеют ожидаемую частоту менее 5. Минимальная ожидаемая частота 7,88.)
Результат получился максимально значимым: участие в партийной работе весьма характерно для государственных служащих, а для предпринимателей — совсем не характерно, тогда как наемные работники находятся посредине. Теперь зададим (кнопкой Statistics...) вывод всех мер связанности для переменных, принадлежащих к номинальной шкале (флажки в группе Nominal).
Directional Measures (Направленные меры)
|
|
Value |
Asympt. Std. Error (a) |
Approx. Т (b) |
Approx. sig. | ||
|
Nominal by Nominal (Номиналь- ный-номина- льный) |
Lambda (Лямбда) |
Symmetric (Симметри- ческая) |
,279 |
,104 |
2,554 |
,011 |
|
Партийная работа Dependent (B зависимости от Партийная работа) |
,357 |
,140 |
,211 |
,035 | ||
|
Занятие Dependent (В зависимости от Занятие) |
,225 |
,106 |
1,930 |
,054 | ||
|
Goodman and Kruskal tau (Tay Гудмена-Крускала) |
Партийная работа Dependent |
,235 |
,093 |
|
,001 (c) | |
|
Занятие Dependent |
,116 |
,051 |
|
,001 (c) | ||
|
Uncertainty Coefficient (Коэффициент неопреде- ленности) |
Симметричный |
,144 |
,063 |
2,269 |
,000 (d) | |
|
Партийная работа Dependent |
,187 |
,082 |
2,269 |
,000 (d) | ||
|
Занятие Dependent |
,118 |
,052 |
2,269 |
,000 (d) | ||
a. Not assuming the null hypothesis (Нулевая гипотеза не принимается).
b. Using the asymptotic standard error assuming the null hypothesis (Используется асимптотическая стандартная ошибка с принятием нулевой гипотезы).
с. Based on chi-square approximation (На основе аппроксимации по распределению хи-квадрат).
d. Likelihood ratio chi-square probability (Степень правдоподобия при распределении вероятности по закону хи-квадрат).
Symmetric Measures (Симметричные меры)
|
|
Value |
Approx. Sig. | |
|
Nominal by Nominal (Номинальный-номинальный) |
Phi (Фи) |
,484 |
,001 |
|
Cramer's V (V Крамера) |
,484 |
,001 | |
|
Contingency Coefficient (Коэффициент сопряженности признаков) |
,436 |
,001 | |
|
N of Valid Cases |
64 |
| |
a. Not assuming the null hypothesis (Нулевая гипотеза не принимается).
b. Using the asymptotic standard error assuming the null hypothesis (Используется асимптотическая стандартная ошибка с принятием нулевой гипотезы).
Коэффициент сопряженности признаков (Пирсона)
Его величина всегда находится в пределах от 0 до 1 и вычисляется (как и значения критериев Фишера (<р) и Крамера (V)) с использованием значения критерия хи-квадрат:
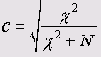
Здесь N — общая сумма частот в таблице сопряженности. Так как N всегда больше нуля, коэффициент сопряженности признаков никогда не достигает единицы. Максимальное значение зависит от количества строк и столбцов таблицы сопряженности и в таблице размером 3*2 составляет (как в данном примере) 0,762. По этой причине коэффициенты сопряженности признаков для двух таблиц с разным количеством полей несопоставимы.
Критерий Фишера (<р)
Этот коэффициент можно использовать только для таблиц 2*2, так как в других случаях он может превысить значение 1:
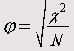
Критерий Крамера (V)
Этот критерий представляет собой модификацию критерия Фишера и для любых таблиц сопряженности он дает значение в пределах от 0 до 1, включая 1:
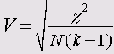
Здесь k — наименьшее из количеств строк и столбцов.
Три названных критерия основаны на использовании критерия хи-квадрат. Они различными способами нормируют его значение по отношению к размеру выборки. Так, если формуле для V Крамера положить k = 2, то значения (р и V Крамера совпадут. Определение значимости основано на значении критерия хи-квадрат.
При оценке полученных значений мер связанности, находящихся в нашем примере в промежутке между 0,4 и 0,5, следует учесть, что значение 1 достигается очень редко или вообще никогда. Другие меры связанности (Я, т Гудмена-Крускала и коэффициент неопределенности) определяются на основе так называемой концепции пропорционального сокращения ошибки. При определении этих критериев одна переменная рассматривается как зависимая; по этой причине данные критерии называются "направленными мерами".
Лямбда
В данном примере вопрос о партийной работе можно рассматривать как зависимую переменную, определяемую родом занятий. Если для какого-то отдельно взятого человека надо сделать предположение о том, выполняет ли он партийную работу или нет, то, естественно, делается наиболее вероятное предположение, соответствующее наиболее часто даваемому ответу — в данном случае, предположение о том, что опрашиваемый занимается партийной работой. Такой ответ дают 56,3% респондентов; однако в 43,7% наблюдений наше предположение будет неверным.
Вероятность предположения можно повысить, если учитывать другую переменную — род занятий. Для наемных работников, как и для государственных служащих, можно достаточно уверенно прогнозировать участие в партийной работе, причем этот прогноз окажется неверным для 9 наемных работников и для 2 государственных служащих. В то же время для предпринимателей можно с большими основаниями предположить, что они не занимаются партийной работой, и ошибиться в 7 наблюдениях. Таким образом, для общего числа 64 опрашиваемых мы получаем 9 + 2 + 7=18 наблюдений, или 28,1 %, в которых прогноз будет неверен. Легко видеть, что первоначальная вероятность ошибки 43,7% значительно сократилась.
На основе этих двух вероятностей можно вычислить относительное сокращение ошибки, которое и называется лямбда:
Лямбда=(Ошибка при первом прогнозе — Ошибка при втором прогнозе)/Ошибка при первом
В нашем примере:
Лямбда =( 43,7% - 28.1%)/43,7% = ,357
Если ошибка при втором прогнозе сокращается до 0, лямбда будет равна 1. Если ошибки при первом и при втором прогнозе одинаковы, лямбда = 0. В этом случае вторая переменная никак не помогает в уточнении предсказания значения первой (зависимой переменной); то есть выбранные две переменные совершенно не зависят друг от друга.
Так как ваш быстрый, но совершенно не умеющий соображать компьютер не знает, какую переменную следует считать зависимой, SPSS вычисляет оба значения Я, поочередно рассматривая каждую из переменных как зависимую. В случае, если выясняется, что ни одну из выбранных переменных нельзя объявить зависимой, выводится среднее двух этих значений с обозначением "лямбда -симметричная".
Тау (т) Гудмена-Крускала
Это вариант меры связанности , который SPSS всегда вычисляет совместно с ней. При определении этой меры количество правильных предсказаний определяется по-иному: наблюдаемые частоты взвешиваются с учетом своих процентов и складываются. Для первого прогноза это дает:
36 * 56,3% + 28 * 43,8% =32,53
Согласно этому выражению, из 64 респондентов неверное предположение сделано для 31,47, что составляет 49,17%.
С учетом второй переменной количество верных предположений (второй прогноз) составляет:
13 * 59,1 % + 16 * 88,9 % + 7 * 29,2 % + 9 * 40,9 % + 2 * 11,1 % + 17 * 70,8 % = 39,89
Итак, при втором прогнозе сделано 24,11 неверных прогнозов из 64, что составляет 37,67%. Тогда сокращение ошибки равно
(49.17 %-37.67%)/49,17 %=0,235
Это значение выводится под названием "тау Гудмена-Крускала". И в этом случае SPSS выдает второе значение т, рассматривая вторую переменную, как зависимую.
Коэффициент неопределенности
Это еще один вариант критерия лямбда, при определении которого имеется в виду не ошибочное предсказание, а "неопределенность", то есть степень неточности предсказаний. Эта неопределенность вычисляется по достаточно сложным формулам, которые мы опускаем. Коэффициент неопределенности также принимает значения в диапазоне от 0 до 1. Значение 1 говорит о том, что одну переменную можно точно предсказать по значениям другой.
Меры связанности для переменных с порядковой шкалой
11.3.4 Меры связанности для переменных с порядковой шкалой
Все эти критерии основаны на количестве нарушений порядка (так называемых инверсий, обозначаемых через 1). Количество инверсий можно определить, если расположить в порядке возрастания значения одной из двух переменной между которыми необходимо установить степень взаимосвязи, а рядом с ними записать соответствующие значения другой переменной. Число нарушений порядка расположения второй переменной и есть количество инверсий. Это количество вместе с количеством соблюдений порядка (проверсий, обозначаемых через Р) используется в различных формулах для определения меры связанности, которые дают значения этого параметра в диапазоне от -1 до +1.
Гамма (ÿ)
Гамма вычисляется по простой формуле:
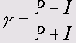
Если инверсий не наблюдается (I = 0), то мы имеем у =1 (полную зависимость). Если же не встречается проверсий, а только инверсии (Р = 0), то говорят о максимально разнонаправленной зависимости (у = -1). Если Р= I, зависимости вообще не существует (y=0).
d Сомера
Существуют две асимметричных и симметричная меры связанности d Сомера. Для их вычисления используется формула для ус корректирующим членом Т, который учитывает количество связей зависимых переменных (одинаковых значений, встречающихся в измерениях):
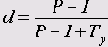
Для сопряженной асимметричной меры связанности d Сомера используется корректирующий член Г, соответствующий количеству связей независимой переменной. В знаменателе симметричной rf-статистики Сомера стоит среднее значение двух асимметричных коэффициентов.
Тау-б (Tb Кендалла)
Этот коэффициент одновременно учитывает связи как зависимых, так и независимых переменных:
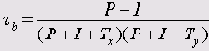
tb может приобретать значения -1 и +1 только для квадратных таблиц сопряженности.
Тау-ц (tc) Кендалла
Этот критерий может достигать значений -1 и +1 в любых таблицах:
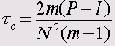
Здесь N — общая сумма частот; m — наименьшее из количеств строк и столбцов.
Другие меры связанности
11.3.5 Другие меры связанности
SPSS позволяет вычислить другие специальные меры связанности, обзор которых приводится ниже.
Эта
Этот коэффициент применяется, если зависимая переменная принадлежит к интервальной шкале, а независимая — к порядковой или шкале наименований, эта2 представляет собой долю общей дисперсии, которую можно объяснить влиянием независимой переменной.
Коэффициент каппа (к)
Коэффициент каппа Козна (к) можно вычислить только для квадратных таблиц сопряженности, в которых применяются одинаковые числовые кодировки для переменных строк и столбцов. Типичный случай применения этого критерия — оценка людей или объектов двумя экспертами. В таком случае к указывает на степень согласия между экспертами.
Мера риска
С помощью этой опции в SPSS реализован расчет трех различных коэффициентов, которые могут быть определены для таблицы сопряженности, состоящей из 2 строк и 2 столбцов, созданной на основании строго определенных правил, которые будут сформулированы в конце данного параграфа. При расчете меры риска анализируется так называемая переменная риска, которая имеет две категории и указывает, произошло ли определенное событие или нет. Анализ переменной риска проводится в зависимости от причинной (независимой) переменной, которая должна также быть дихотомической.
Это положение можно пояснить на типичном примере. Исследование депрессии на базе 294 респондентов дало следующую частотную таблицу:
| Депрессия | Да | Нет |
| Женщины | а = 40 | Ь = 143 |
| Мужчины | с = 10 | d = 101 |
Обе переменные, входящие в таблицу, — являются дихотомическими. Депрессия, имеющая две категории (да-нет), является переменной риска, а пол с двумя категориями (женщины-мужчины) — независимой (причинной) переменной.
Исследование, проводимое в такой форме, называется групповым или когортным. При когортном исследовании определенная группа наблюдений, в которых анализируемое событие еще не произошло, изучается на протяжении известного промежутка времени. Определяется, в каких наблюдениях данное событие произошло, а в каких — нет, и различается ли риск наступления события между разными категориями независимой переменной. При групповых исследованиях группа наблюдений, в которых событие уже произошло, сравнивается с контрольной группой.
Два из трех коэффициентов риска, определяемых в SPSS, обычно относятся к когортным исследованиям, а третий — к групповым. При когортном исследовании для обеих категорий независимой переменной (в данном случае пола) определяется инцидентность. У респондентов-женщин инцидентность наступления депрессии равна:
40/(40 + 143)=0,219
У респондентов-мужчин инцидентность равна
10/(10 + 101)=0,09
Отношение инцидентностей составляет
0,219/0,090 = 2,426
и называется относительным риском или мерой относительного риска. Риск попасть в депрессию у женщин в 2,426 раза выше, чем у мужчин. Так как компьютер не знает, какое из двух кодовых значений переменной риска соответствует наличию депрессии, относительный риск вычисляется для обоих значений.
При групповом исследовании применяется несколько отличный вариант коэффициента, называемый также "отношением шансов" (отношением перекрестных произведений). "Шансы" попасть в депрессию у женщин составляют 40/143, а у мужчин — 10/101. Следовательно, отношение шансов равно
(40 * 101)/(143 * 10)= 2,825
Если обозначить четыре частоты в таблице буквами а, Ь, с и d (см. выше), то формулы, которые SPSS использует для вычисления мер риска, можно записать так:
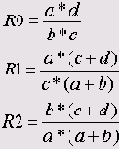
Проведем анализ приведенного примера в SPSS.
Загрузите файл depr.sav.
Этот файл содержит переменную риска depr с кодовыми значениями 1 = да и 2 = нет и независимую (причинную) переменную sex с кодовыми значениями 1 = женщины и 2 = мужчины. Еще одна переменная, n, содержит частоты наблюдений.
Выберите в меню команды Data (Данные) Weight Cases... (Взвесить наблюдения) и задайте n как переменную взвешивания.
В диалоговом окне Crosstabs определите переменную sex как переменную строк и depr — как переменную столбцов, а во вспомогательном диалоге Statistics установите флажок Risk (Риск).
В окне просмотра будут показаны следующие результаты.
Пол * Депрессия Таблица сопряженности
| Депрессия | Total | |||
| да | нет | |||
| Пол | Женщины | 40 | 143 | 183 |
| Мужчины | 10 50 | 101 | 111 | |
| Total | 244 | 294 |
Risk Estimate (Оценка риска)
| Value | 95% Confidence Interval (95% доверительный интервал) | ||
| Lower (Нижняя граница) | Upper (Верхняя граница) | ||
| Odds Ratio for (Отношение шансов для) Пол (Женщины / Мужчины) | 2,825 | 1,350 | 5,911 |
| For cohort (Для когорты) Депрессия = да | 2,426 | 1,265 | 4,655 |
| For cohort (Для когорты) Депрессия = нет | ,859 | ,780 | ,946 |
| N of Valid Cases | 294 |
Здесь последовательно показаны отношение шансов (RO) и оба коэффициента относительного риска (R1 и R2). Кроме того, для каждой величины определен 95 % доверительный интервал.
Чтобы правильно вычислить отношение шансов и относительный риск, надо учитывать следующие правила построения таблиц сопряженности:
Определяйте причинную (независимую) переменную как переменную строк, а переменную риска — как переменную столбцов.
В первой ячейке каждой строки таблицы должна находиться группа с наибольшим риском.
В первой ячейке каждого столбца таблицы должно стоять кодовое значение совершения события.
Тест хи-квадрат по Мак-Немару
Тест хи-квадрат по Мак-Немару применяется при наличии двух независимых дихотомических переменных; он рассматривается в разделе 14.2.
Статистика Кохрана и Мантеля-Хзнзеля
Эта статистика включает метод вычисления отношения шансов в таблицах сопряженности 2x2. Расчет этой статистики задается флажком Risk. При вычислениях используется переменная слоев (ковариация) и определяется, значительно ли отличаются категории этой переменной по своему отношению шансов от 1 (или другой величины). Это можно пояснить на примере.
Загрузите файл angst.sav.
В этом файле в трех переменных хранятся сведения о 1737 людях: их пол (1 = женский, 2 = мужской), наличие тревожной депрессии (1 = да, 2 = нет) и избыточного веса (1 = нет, 2 = да). Для людей с избыточным весом и с недостатком веса составим раздельные таблицы сопряженности пола и наличия тревожной депрессии, а затем вычислим отношение шансов.
Выберите в меню команды Data (Данные) Split File... (Разделить файл)
Выберите опцию Organize output by groups (Разделить вывод на группы) и задайте gewicht как группирующую переменную.
Выберите команды меню Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Crosstabs... (Таблицы сопряженности)
Перенесите переменную sex в список переменных строк, а переменную angst — в список переменных столбцов.
Кнопкой Cells... (Ячейки) задайте вывод процентов по строкам (Percentages — Row), а кнопкой Statistics... (Статистика) — вывод риска (Risk):
Основная часть результатов приводится ниже.
Пол * Тревожная депрессия Crosstabulation (a)
| Тревожная депрессия | Total | ||||
| Да | нет | ||||
| Пол | женский | Count | 154 | 592 | 746 |
| % от Пол | 20,6% | 79,4% | 100,0% | ||
| мужской | Count | 79 | 715 | 794 | |
| % от Пол | 9,9% | 90,1% | 100,0% | ||
| Total | Count | 233 | 1307 | 1540 | |
| % от Пол | 15,1% | 84,9% | 100,0% | ||
| Избыточный вес = нет |
Risk Estimate (a)
| 95% Confidence Interval
| |||
| Value | Lower | Upper | |
| Odds Ratio for Пол (женский / мужской) | 2,354 | 1,758 | 3,154 |
| For cohort Тревожная депрессия = да | 2,075 | 1,612 | 2,670 |
| For cohort Тревожная депрессия = нет | ,881 | ,844 | ,920 |
| N of Valid Cases | 1540 | ||
| а. Избыточный вес = нет |
Пол * Тревожная депрессия Crosstabulation (a)
| Тревожная депрессия | Total | ||||
| Да | нет | ||||
| Пол | женский | Count | 22 | 62 | 84 |
| % от Пол | 26,2% | 73,8% | 100,0% | ||
| мужской | Count | 9 | 104 | 113 | |
| % от Пол | 8,0% | 92,0% | 100,0% | ||
| Total | Count | 31 | 166 | 197 | |
| % от Пол | 15,7% | 84,3% | 100,0% | ||
| Избыточный вес; = да |
Risk Estimate (a)
| Value | 95% Confidence Interval | ||
| Lower | Upper | ||
| Odds Ratio for Пол (женский / мужской) | 4,100 | 1,776 | 9,468 |
| For cohort Тревожная депрессия = да | 3,288 | 1,597 | 6,771 |
| For cohort Тревожная депрессия = нет | ,802 | ,698 | ,921 |
| N of Valid Cases | 197 |
а. Избыточный вес = да
В обоих случаях тревожная депрессия у женщин наступает значительно чаще. Отношение шансов для людей с недостатком веса составляет 2,354, а для людей с избыточным весом — 4,100.
Теперь вычислим статистику Кохрана и Мантеля-Хэнзеля.
Чтобы отменить разделение на группы, после вызова команд меню Data (Данные) Split File... (Разделить файл) выберите опцию Analyze all cases, do not create groups (Анализировать все наблюдения, не создавать группы).
В диалоговом окне Crosstabs задайте gewicht как переменную слоев, во вспомогательном диалоге Statistics снимите флажок Risk и установите флажок Cochran and Mantel-Haenszel statistics (Статистика Кохрана и Мантеля-Гензеля).
В поле Test common odds ratio equals (Общее отношение шансов) оставьте значение 1, установленное по умолчанию.
Из полученных результатов ниже приводится только статистика Кохрана и Мантеля-Гензеля.
Test of Homogenity of the Odds Ratio (Тест на гомогенность отношения шансов) Statistics
| Statistics | Chi-Squared (Хи-квадрат) | df | Asymp. Sig. (2-sided) | |
| Conditional (Условная независимость) | Cochran (Кохран) | 44,665 | 1 | ,000 |
| Mantel-Haenszel (Мантель-Гензель) | 43,724 | 1 | ,000 | |
| Homogeneity (Гомогенность) | Breslow-Day (Бреслоу-Дэй) | 1,522 | 1 | ,217 |
| Tarone (Тарой) | 1,522 | 1 | ,217 |
Under the conditional independence assumption, Cochran's statistic is asymptotically distributed as a 1 df chi-squared distribution, only if the number of strata is fixed, while the Mantel-Haenszel statistic is always asymptotically distributed as a 1 df chi-squared distribution. Note that the continuity correction is removed from the Mantel-Haenszel statistic when the sum of the differences between the observed and the expected is 0. (При гипотезе условной независимости статистика Кохрана дает распределение, асимптотически приближающееся к распределению хи-квадрат с 1-ой степенью свободы, только при фиксированном количестве слоев, в то время как статистика Мантеля-Хэнзеля при той же гипотезе всегда дает такое распределение. Обратите внимание, что в статистике Мантеля-Хэнзеля опускается коррекция на непрерывность, если сумма разностей наблюдаемых и ожидаемых величин равна 0.)
Mantel-Haenszel Common Odds Ratio Estimate (Оценка общего отношения шансов Мантеля-Гензеля)
| Estimate (Оценка) | 2,503 | ||
| ln(Estimate) | ,918 | ||
| Std. Error of (Стандартная ошибка) In(Estimate) | ,141 | ||
| Asymp. Sig. (2-sided) (Асимптотическая значимость (двусторонняя) | ,000 | ||
| Asymp. 95% Confidence Interval (Асимптотический 95 % доверительный интервал) | Common Odds Ratio (Общее отношение шансов) | Lower Bound (Нижняя граница) | 1,901 |
| Upper Bound (Верхняя граница) | 3,297 | ||
| ln(Common Odds Ratio) | Lower Bound (Нижняя граница) | ,642 | |
| Upper Bound (Верхняя граница) | 1,193 |
The Mantel-Haenszel common odds ratio estimate is asymptotically normally distributed under the common odds ratio of 1,000 assumption. So is the natural log of the estimate. (Оценка общего отношения шансов Мантеля-Хэнзеля при условии, что общее отношение шансов равно 1,000, имеет асимптотически нормальное распределение. То же распределение сохраняется и для натурального логарифма оценки.)
Результаты тестов Кохрана и Мантеля-Хэнзеля очень близки; в обоих случаях для весовых групп наблюдается максимально значимое отличие отношения шансов от 1 (р<0,001). Тесты как Бреслоу-Дэя, так и Тарона позволяют сохранить допущение о гомогенности отношения шансов для весовых групп (р = 0,217).
Оценка объединенного отношения шансов дает те значения, которые будут получены при вычислении риска, если не разделять данные по переменной слоев.
Статистические критерии для таблиц сопряженности
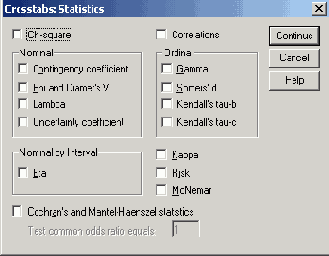
11.3 Статистические критерии для таблиц сопряженности
Чтобы получить статистические критерии для таблиц сопряженности, щелкните на кнопке Statistics... (Статистика) в диалоговом окне Crosstabs. Откроется диалоговое окно Crosstabs: Statistics (Таблицы сопряженности: Статистика) (см. рис. 11.9).
Флажки в этом диалоговом окне позволяют выбрать один или несколько критериев.
Тест хи-квадрат (X2)
Корреляции
Меры связанности для переменных, относящихся к номинальной шкале
Меры связанности для переменных, относящихся к порядковой шкале
Меры связанности для переменных, относящихся к интервальной шкале
Коэффициент каппа (к)
Диалоговое окно Crosstabs: Cell Display
Диалоговое окно Crosstabs: Cell Display
Установите флажок Expected.
Щелкните на кнопке Continue, а затем на ОК. Вы получите следующую таблицу сопряженности.
Пол * Психическое состояние Crosstabulation (Таблица сопряженности)
|
Психическое состояние | |||||||
|
Крайне неустой-чивое |
Неусто- йчивое |
Устой-чивое |
Очень устой-чивое |
Total | |||
|
Пол |
женский |
Count |
16 |
18 |
9 |
1 |
44 |
|
|
Expected Count (Ожида- емое число) |
|
|
|
|
| |
|
|
7,9 |
16,6 |
17,0 |
2,5 |
44,0 | ||
|
|
|
|
|
|
| ||
|
|
мужской |
Count |
3 |
22 |
32 |
5 |
62 |
|
|
Expected Count |
11,1 |
23,4 |
24,0 |
3,5 |
62,0 | |
|
"Total |
Count |
19 |
40 |
41 |
6 |
106 | |
|
Expected Count |
19,0 |
40,0 |
41,0 |
6,0 |
106,0 | ||
|
|
|
|
|
| |||
Теперь под наблюдаемыми частотами (Count) появились ожидаемые значения Expected Count). Эти данные мы можем интерпретировать так:
Для значений переменной "психическое состояние" "крайне неустойчивое" и "неустойчивое" абсолютная частота у опрашиваемых женщин выше, чем ожидаемая (16 и 7,9; j и 16,6), тогда как при значениях "устойчивое" и "очень устойчивое" она ниже (9 и ".0; 1 и 2,5).
У опрашиваемых мужчин мы находим противоположную тенденцию. Для значений ' крайне неустойчивое" и "неустойчивое" абсолютная частота ниже, чем ожидаемая (3 и ' 1.1; 22 и 23,4), тогда как для значений "устойчивое" и "очень устойчивое" она выше :2 и 24,0; 5и 3,5). Эти результаты мы можем объединить в следующую таблицу:
|
|
крайне неустойчивое; неустойчивое |
очень устойчивое; устойчивое |
| Женщины | абс. частота > ожидаемой частоты | абс. частота < ожидаемой частоты |
|
Мужщины
|
абс. частота < ожидаемой частоты |
абс. частота > ожидаемой частоты |
Таким образом, наше первоначальное впечатление, что женщины считают свое психическое состояние менее устойчивым, чем мужчины, подтверждается. Еще одну возможность выявления существования зависимости между переменными дает вычисление остатков. Эти остатки являются показателем того, насколько сильно наблюдаемые и ожидаемые частоты отклоняются друг от друга. Чтобы получить остатки частот, выполните следующие действия:
Выберите в меню команды Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Crosstabs... (Таблицы сопряженности)
В списке переменных строк у нас должна стоять переменная sex, а в списке переменных столбцов — переменная psyche.
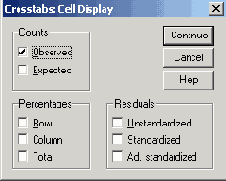
Щелкните на кнопке Cells... Флажки Observed и Expected следует оставить помеченными.
В группе Residuals (Остатки) можно выбрать один или более следующих вариантов отображения:
Unstandardized (Ненормированные): Отображаются ненормированные остатки, то есть разность наблюдаемых (f) и ожидаемых (f) частот.
Standardized (Нормированные): Отображаются нормированные остатки. Для этого ненормированные остатки делятся на квадратный корень из ожидаемой частоты: