Коэффициент корреляции Пирсона

15.1 Коэффициент корреляции Пирсона

Данный коэффициент вычисляется по следующей формуле:

Ранговые коэффициенты корреляции по Спирману и Кендалу

15.2 Ранговые коэффициенты корреляции по Спирману и Кендалу

Для переменных, принадлежащих к порядковой шкале или для переменных, не подчиняющихся нормальному распределению, а также для переменных принадлежащих к интервальной шкале, вместо коэффициента Пирсона рассчитывается ранговая корреляция по Спирману. Для этого отдельным значениям переменных присваиваются ранговые места, которые впоследствии обрабатываются с помощью соответствующих формул. Чтобы выявить ранговую корреляцию, уберите в диалоговом окне Bivariate Correlations... (Парные корреляции) метку для расчета корреляции по Пирсону, установленную по умолчанию. Вместо этого активируйте расчет корреляции Спирмана. Это расчет даст следующие результаты (см. стр. 260).

Коэффициенты ранговой корреляции весьма близки к соответствующим значениям коэффициентов Пирсона (исходные переменные имеют нормальное распределение). Ещё одним вариантом ранговых коэффициентов корреляции являются коэффициенты Кендала (tb Кендала), расчет которых можно вызвать в диалоговом окне Bivariate Correlations... (Парные корреляции). В этом методе одна переменная представляется в виде монотонной последовательности в порядке возрастания величин; другой переменной присваиваются соответствующие ранговые места. Количество инверсий (нарушений монотонности по сравнению с первым рядом) используется в формуле для корреляционных коэффициентов. Применение коэффициента Кендала является предпочтительным, если в исходных данных встречаются выбросы.

Correlations (Корреляции)

			Chole- sterin, Ausgan-gswert (Холе-стерин, исходная величина)	Chole-sterin, nach 1 Monat (Холе-стерин, через 1 месяц)	Chole-sterin, nach 6 Monaten (Холе-стерин, через 6 месяцев)	Chole- sterin, nach 12 Monaten (Холе-стерин, через 12 месяцев)
Spearman's rho (рСпир-мана)	Chole-sterin, Ausgang-swert (Холес-терин, исходная величина)	Correlation Coefficient (Коэф- фициент корре- ляции) Sig. (2-tailed) (Значимость (2-сторонняя)) N	1,000 174	,877" ,000 174	,791" ,000 174	,792"! ,000 174
	Chole-sterin, nach 1 Monat (Холес-терин, через 1 месяц)	Correlation Coefficient (Коэф- фициент корре- ляции) Sig. (2-tailed) (Значимость (2-сторонняя)) N	,877" ,000 174	1,000 174	,874** ,000 174	,834" ,000 174
	Chole-sterin, nach 6 Monaten (Холес-терин, через 6 месяцев)	Correlation Coefficient (Коэф- фициент корр-еляции) Sig. (2-tailed) (Значимость (2-сторонняя)) N	,791** ,000 174	,874** ,000 174	1,000 174	,879" ,000 174
	Choles-terin, nach 12 Monaten (Холес-терин, через 12 месяцев)	Correlation Coefficient (Коэф- фициент корре- ляции) Sig. (2-tailed) (Значимость (2-сторонняя)) N	,792** ,000 174	.834" ,000 174	,879" ,000 174	1,000 174

** Correlation is significant at the .01 level (2-tailed). (Корреляция является значимой на уровне 0,01 (2-сгороння)).

Если рассчитать корреляционную матрицу Кендала, то станет заметно, что в данном случае коэффициенты значительно ниже корреляционных коэффициентов Спирмана.

Частная корреляция

15.3 Частная корреляция

Если исследовать достаточно большую совокупность мужчин и сопоставить размер их обуви с уровнем образованности, то между этими двумя переменными можно заметить хоть и небольшую, но в то же время значимую корреляцию. Это корреляция может послужить примером так называемой ложной корреляции. Здесь статистически значимый коэффициент корреляции является не проявлением некоторой причинной связи между двумя рассматриваемыми переменными, а в большей степени обусловлен некоторой третьей переменной.

В рассматриваемом примере такой переменной является рост. С одной стороны существует некоторая незначительная корреляция между ростом и уровнем образованности, а с другой — вполне объяснимая и логичная связь между ростом и размером обуви. Вместе эти две корреляции приводят к упоминавшейся ложной корреляции. Для исключения одной такой искажающей переменной необходим расчёт так называемой частной корреляции.

Если присвоить коррелирующим переменным индексы 1 и 2, а искажающей переменной — индекс 3, и попарно рассчитать корреляционный коэффициент (Пирсона) r12,r13, и r23 , то для частных корреляционных коэффициентов получим:

Мера расстояния и мера сходства

15.4 Мера расстояния и мера сходства

Наряду с приведенными корреляционными коэффициентами, SPSS дополнительно предлагает расчет ряда мер расстояния и мер сходства. Так, к примеру, реализован расчет многочисленных мер сходства при анализе взаимосвязи между дихотомическими переменными. Некоторые статистические процедуры, такие как факторный анализ, кластерный анализ, многомерное масштабирование, построены на применении этих мер, а иногда сами представляют добавочные возможности для вычисления 1 ер подобия. Если Вы во время выполнения этих процедур захотите использовать какую-либо меру, не предусмотренную в выбранной процедуре, то Вам следует воспользоваться дополнительными возможностями, предоставляемыми SPSS.

В качестве примера возьмем анкету, которая будет рассматриваться в главе 21. Она посвящена исследованию степени любознательности опрашиваемых.

Откройте файл neugier.sav.

Выберите в меню Analyze... (Анализ) Correlate... (Корреляция) Distances... (Расстояния)

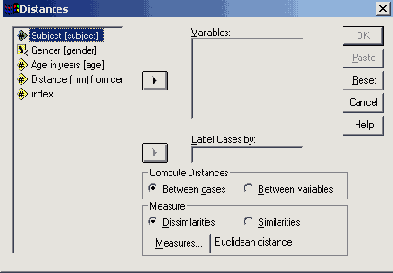
Появится диалоговое окно Distances... (Расстояния).

В этом диалоговом окне Вы можете организовать расчет расстояния между наблюдениями или между переменными, а также выбрать тип рассчитываемой меры мера отличия или мера подобия). Щелчком на кнопке Measures... (Меры) можно выбрать формулу вычисления меры расстояния для интервальных или дихотомических (бинарных) переменных. В основу расчета мер отличия могут быть также положены и частоты.

Все меры отличия и сходства для переменных, принадлежащих к интервальной шкале, будут рассмотрены в главе 20.3. Эти меры являются важным элементом кластерного анализа. Ниже приведены формулы для мер сходства между бинарными (дихотомическими) переменными, принадлежащими к интервальной шкале. Символами а, b, с и d обозначены частоты, находящиеся в ячейках таблицы 2x2 (четырёхполевой таблицы). В случае необходимости, более подробное объяснение этих формул Вы найдёте в главе 20.3.3.

Внутриклассовый коэффициент корреляции (Intraclass Correlation Coefficient (ICC))

15.5 Внутриклассовый коэффициент корреляции (Intraclass Correlation Coefficient (ICC))

Внутриклассовый коэффициент корреляции (ICC) со значениями, находящимися в диапазоне между -1 и +1, применяется в качестве меры связанности в том случае, когда согласованность двух признаков должна быть проверена не так, как при расчете рассмотренных выше корреляционных коэффициентов, относительно её общей направленности ("чем больше одна переменная, тем больше вторая"), а также и относительно средних уровней обеих переменных. Таким образом, расчёт ICC считается уместным только тогда, когда обе переменные имеют приблизительно одинаковый уровень значений. Подобная ситуация вероятнее всего возникнет в случае, когда одной и той же величине дается двоякая оценка.

ICC играет также важную роль при анализе достоверности (гл. 21), где он применяется в качестве меры достоверности. При его расчёте используется более двух переменных, называемых в данном случае объектами. В связи с этим расчёт ICC в SPSS производится в рамках анализа достоверности.

Рассмотрим расчёт ICC на данных одного типичного примера.

Откройте файл alter.sav.

В файле находятся три переменные: a, agesch и agesch10. Переменной а обозначен фактический возраст респондентов, agesch — возраст по оценке со стороны. Переменная agesch10 соответствует возрасту по оценке со стороны минус 10 лет.

Если Вы произведёте расчёт корреляционных коэффициентов Пирсона (см. гл. 15.1) для переменных а и agesch, то получите значение г = 0,944. Такое же значение Вы получите при расчёте корреляции между переменными а и agesch2, так как соотношение между обоими переменными не изменилось.

Определим теперь ICC.

Выберите в меню Analyze... (Анализ) Scale... (Масштабировать) Reliability Analysis... (Анализ пригодности)

Перенесите обе переменные а и agesch в список объектов.

Через кнопку Statistics... (Статистика), активируйте опцию Intraclass Correlation Coefficient (Корреляционный коэффициент внутри классов).

В качестве модели выберите One-Way Random (Однократно, случайно), которая соответствует традиционному расчёту ICC.

Оставьте предварительно установленный 95 % доверительный интервал и подтвердите нажатием Continue (Далее) и ОК.

В окне просмотра появятся следующие результаты:

RELIABILITY ANALYSIS - SCALE (ALPHA)

Intraclass Correlation Coefficient

One-way random effect model: People Effect Random

Single Measure Intraclass Correlation = ,9367

95,00% C.I.: Lower = Л9156 Upper = ,9526

F = 30,5740 DF = ( 173, 174,0)

Sig. = ,0000 (Test Value = ,0000 )

Average Measure Intraclass Correlation = , 9673

95,00% C.I.: Lower = ,9559 Upper = ,9757

F = 30,5740 DF = ( 173, 174,0)

Sig. = ,0000 (Test Value = ,0000 )

Reliability Coefficients

N of Cases = 174,0 N of Items = 2

Alpha = ,9680

Результаты обычного расчёта ICC Вы найдёте под заголовком «Single Measure Intraclass Correlation». Вы получите значение ICC = 0,9367, которое с 95 %-м доверительным интервалом принадлежит к диапазону от 0,9156 до 0,9526. Это значение весьма близко к корреляционным коэффициентам Пирсона.

Повторите теперь расчёт для переменных а и agesch10.

В последней переменной из сторонней оценки возраста вычитается постоянная величина. Так как обе переменные теперь имеют различные уровни, то ICC теперь показывает заметно более низкое значение: ICC = 0,6957.

Ещё одним типичным случаем для применения расчёта ICC является определение связей между фактическим весом и весом по оценке со стороны или фактическим и оценочным ростом.

Активируйте расчёт расстояний Between Variables

Частоты в таблице 2x2

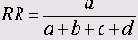
Выберите в меню Analyze... (Анализ) Correlate... (Корреляция) Distances... (Расстояния) Перенесите переменные item3 и item 14 в поле тестируемых переменных. Активируйте расчёт расстояний Between Variables (Между переменными) и в качестве типа меры выберите Similarities... (Подобия). Щёлкните на кнопке Measures... (Меры) и, в открывшемся диалоговом окне, активируйте Binary (Бинарные). Оставьте предварительную установку мер вычисления по методу Рассела и Рао. Так как в приведенном примере отрицательному ответу присвоен код 2, а в предварительных установках предусмотрен 0, то Вам необходимо откорректировать это значение в поле Absent (Отсутствует). Покиньте диалоговое окно мер нажатием Continue (Далее) и в главном диалоговом окне начните расчёт щелчком на ОК. В результате Вы получите значение меры подобия равное 0,3. Оно определяется как частное от деления частоты а на сумму всех четырёх частот:

Proximity Matrix (Матрица близости)

	Russell and Rao Measure (Мера подобия Рассела и Рао)
	ITEM3	ITEM14
ITEM3 ITEM 14	,300	,300

This is a similarity matrix (Это матрица подобия) ;

Пример второй: расчёт корреляционной матрицы 2x2 в качестве базиса для факторного анализа

Мы хотим рассчитать корреляционную матрицу для восемнадцати переменных item1-item18 с применением четырёхточечная корреляция фи. В этом случае корреляционную матрицу можно использовать в качестве базиса для факторного анализа. Для решения этой задачи нам предстоит поработать с программным синтаксисом SPSS.

Перенесите переменные item1-item18 в поле тестируемых переменных. Активируйте расчёт расстояний Between Variables (Между переменными) и в качестве типа меры выберите Similarities... (Подобия). Откройте щелчком на кнопке Measures... (Меры) соответствующее диалоговое окно, активируйте в нём Binary (Бинарные) и присвойте параметру Absent (Отсутствует) код 2. В заключении вместо меры по Расселу и Рао выберите 4 точечную µ-корреляцию. При помощи щелчка на Continue (Далее) вернитесь в основное диалоговое окно, после прохождения кнопки Paste... (Вставить) просмотрите синтаксис команд. Внесите в синтаксис следующие корректировки: PROXIMITIES item1 item2 item3 item4 item5 item6 item7 item8 item9 item10 item11 item12 Lzem13 item14 item15 item16 item17 item18 VIEW=VARIABLE MEASURE= PHI (1,2) MATRIX=OUT(*) . SSCODE rowtype_ ( "PROX"='CORR') . FACTOR /MATRIX=IN(COR=*). Начните расчёт при помощи символа Syntax-Start (Синтаксис-Начать). В окне просмотра появятся результаты факторного анализа, а в окне редактора данных будет показана корреляционная матрица.

Диалоговое окно Bivariate Correlations (Двумерные корреляции)

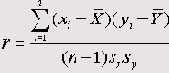
Полученные результаты содержат: корреляционный коэффициент Пирсона r, количество использованных пар значений переменных и вероятность ошибки р, соответствующая предположению о ненулевой корреляции. В приведенном примере присутствует сильная корреляция, поэтому все коэффициенты конечно же являются сверхзначимыми (р < 0,001). Следовательно, маркировка корреляции, приведенная :-низу таблицы, должна была бы состоять из трёх звёздочек, которыми обозначается уровень р=0,001.

При помощи щелчка на кнопке Options... (Опции) можно организовать расчёт среднего значения и стандартного отклонения для двух переменных. Дополнительно могут выводиться отклонения произведений моментов (значений числителя формулы для коэффициента корреляции) и элементы ковариационной матрицы (числитель, делённый на n - 1).

Диалоговое окно Distances... (Расстояния).

Рассел и Рао (Russel and Rao)

Диалоговое окно Partial Correlations (Частичные корреляции)

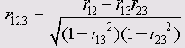
Корреляции

Глава 15. Корреляции

Корреляции 15.1 Коэффициент корреляции Пирсона 15.2 Ранговые коэффициенты корреляции по Спирману и Кендалу 15.3 Частная корреляция 15.4 Мера расстояния и мера сходства 15.5 Внутриклассовый коэффициент корреляции (Intraclass Correlation Coefficient (ICC))

Корреляции

В этой главе речь пойдёт о связи (корреляции) между двумя переменными. Расчёты подобных двумерных критериев взаимосвязи основываются на формировании парных значений, которые образовываются из рассматриваемых зависимых выборок.

Если в качестве примера мы возьмём данные об уровне холестерина для первых двух моментов времени из исследования гипертонии (файл hyper.sav), то в данном случае следует ожидать довольно сильную связь: большие значения в исходный момент времени являются веским поводом для ожидания больших значений и через 1 месяц.

Для графического представления подобной связи можно использовать прямоугольную систему координат с осями, которые соответствуют обеим переменным. Каждая; пара значений маркируется при помощи определенного символа. Такой график, называемый «диаграммой рассеяния» для двух зависимых переменных можно построить путём вызова меню Graphs... (Графики) Scatter plots... (Диаграммы рассеяния) (см. гл. 22.8).

Образовавшееся скопление точек показывает, что обследованные пациенты с высокими исходными показателями, как правило, имеют высокие значения холестерина и при повторном опросе через месяц. Это, конечно же, не является неожиданностью; данный пример был выбран, чтобы продемонстрировать наличие явной связи.

Статистик говорит о корреляции между двумя переменными и указывает силу связи при помощи некоторого критерия взаимосвязи, который получил название коэффициента корреляции. Этот коэффициент, всегда обозначаемый латинской буквой г, может принимать значения между -1 и +1, причём если значение находится ближе к 1, то это означает наличие сильной связи, а если ближе к 0, то слабой.

Диаграммы рассеяния

Рис. 15.1.Диаграммы рассеяния

Если коэффициент корреляции отрицательный, это означает наличие противоположной связи: чем выше значение одной переменной, тем ниже значение другой. Сила связи характеризуется также и абсолютной величиной коэффициента корреляции. Для словесного описания величины коэффициента корреляции используются следуюшие градации:

Значение	Интерпретация
до 0,2	Очень слабая корреляция
до 0,5	Слабая корреляция
до 0,7	Средняя корреляция
до 0,9	Высокая корреляция
свыше 0,9	Очень высокая корреляция

Метод вычисления коэффициента корреляции зависит от вида шкалы, которой относятся переменные.

Переменные с интервальной и с номинальной шкалой: коэффициент корреляции Пирсона (корреляция моментов произведений).

По меньшей мере, одна из двух переменных имеет порядковую шкалу либо не является нормально распределённой: ранговая корреляция по Спирману или т (тау-грого-соая) Кендала.

Одна из двух переменных является дихотомической: точечная двухрядная корреляция. Эта возможность в SPSS отсутствует. Вместо этого может быть применён расчёт ранговой корреляции.

Обе переменные являются дихотомическими: четырёхполевая корреляция. Данный вид корреляции рассчитываются в SPSS на основании определения мер расстояния и мер сходства (см. гл 15.4).

Расчёт коэффициента корреляции между двумя недихотомическими переменными не лишён смысла только тогда, кода связь между ними линейна (однонаправлена). Если связь, к примеру, U-образная (неоднозначная), то коэффициент корреляции непригоден для использования в качестве меры силы связи: его значение стремится к нулю. В следующих разделах будут рассмотрены корреляции по Пирсону, Спирману и Кендалу. Ешё один раздел специально посвящён частной корреляции.