Учебник по контролю качества
Рассматриваемые факты
Ручка реостата, изготовленная из пластмассы с помощью формы, имеет металлическую вставку, приобретаемую у поставщика. Собранное из этих двух деталей изделие должно иметь строго определенный размер. Эта величина, которая зависит как от металлической вставки, так и от формовочной операции, задается техническим отделом в пределах 0.140 ± 0.003 дюйма. Многие отформованные ручки при прохождении 100% контроля датчиками по принципу “годен – не годен” отбраковываются при обнаружении выхода за заданный допуск.
Был спроектирован и создан специальный прибор, позволяющий проводить быстрое измерение фактического значения этой величины. С помощью этого прибора измеряются пять произведенных ручек в течение часа. Таблица 1 содержит эти размеры, полученные за первые два дня работы прибора (Вы можете скачать файл данных в формате STATISTICA здесь).
Таблица 1Таблица 1
| Номер выборки | Измерение каждой детали (по пять деталей в час) |
Среднее |
Размах |
||||
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
140 138 139 143 142 136 142 143 141 142 137 137 142 137 144 140 137 137 142 136 142 139 140 134 138 140 145 |
143 143 133 141 142 144 147 137 142 137 147 146 142 145 142 132 137 142 142 142 144 146 145 147 145 145 145 |
137 143 147 137 145 143 137 145 147 145 142 142 139 144 143 144 142 142 143 140 140 143 142 143 141 143 137 |
134 145 148 138 135 136 142 137 140 140 137 142 141 137 135 145 143 145 140 139 138 140 139 141 137 144 138 |
135 146 139 140 136 137 138 138 140 132 135 140 142 140 144 141 141 143 135 137 143 139 137 142 141 138 140 |
137.8 143.0 141.2 139.8 140.0 139.2 141.2 140.0 142.0 139.2 139.6 141.4 141.2 140.6 141.6 140.4 140.0 141.8 140.4 138.8 141.4 141.4 140.6 141.4 140.4 142.0 141.0 |
9 8 15 6 10 8 10 8 7 13 12 9 3 8 9 13 6 8 8 6 6 7 8 13 8 7 8 |
| Всего | 3797.4 | 233 |
Таблица 1. Измерения расстояний
от задней части ручки реостата до отверстия под штифт
(Указаны значения в 0.001 дюйма)
Проведение анализа фактов
с помощью методики контрольных карт На Рисунках 2 и 3 показаны контрольные карты


Если мы подсчитаем все точки, лежащие вне доверительных пределов на Рисунке 1, мы обнаружим, что 42 из 135 ручек не удовлетворяют заданным спецификациям для размеров. Уровень несоответствия весьма высок и равен примерно 31%.
В то же время очевидно, что все точки на






UCL

UCL

UCLR (верхний контрольный предел для размахов) = 18.2
UCLR (нижний контрольный предел для размахов) = 0
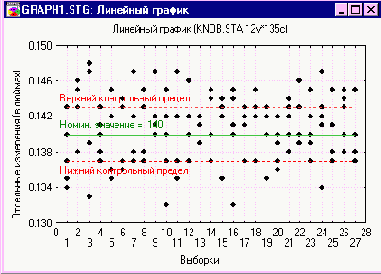
Рисунок 1. Исходные измерения

Рисунок 2.


Рисунок 3.

Этот процесс, очевидно, удовлетворяет статистическому контролю, несмотря на то, что он имеет диапазон отклонений, который неудовлетворителен с точки зрения заданного допуска ± 0.003 дюйма. Не было обнаружено неслучайных причин изменчивости. Отклонения от часа к часу являются случайными отклонениями; они не могут быть уменьшены путем отыскания изменений, которые происходят от часа к часу. В такой ситуации улучшения не могут быть достигнуты путем оказания давления со стороны дирекции завода на инспектора цеха или путем оказания давления инспектором на оператора машины.
Действия в связи с анализом контрольных карт Когда инженер по контролю качества на данном заводе изучил ситуацию, обнаружилось, что хотя часть разброса значений данной величины объяснялась изменчивостью формовочной операции, более важным фактором являлась изменчивость металлических вставок, полученных от стороннего поставщика. Поскольку эта деталь является существенной для важного контракта, и количество доступных поставщиков ограничено, ничего не может быть сделано непосредственно с металлической вставкой.
Оставались только две альтернативы: продолжать исключать многие детали при 100% контроле либо расширить границы допуска. Инженер по контролю качества сделал запрос в технический отдел о пересмотре границ допуска. Этот пересмотр показал, что заданный допуск ± 0.003 дюйма был более узок, чем требовалось для удовлетворительного функционирования ручки реостата как составной части. Проверка ручек с различными значениями этой величины и экспертиза качества подгонки деталей показали возможность изменения границ допуска:
+ 0.010
- 0.015
Таблица 1 и Рисунок 1 позволяют сделать вывод, что при этих пересмотренных границах допуска все детали в 27 выборках по пять деталей были бы приняты. С изменением допуска и установлением факта удовлетворения процесса статистическому контролю становится возможным использование контрольных карт взамен 100% контроля данной величины.
Последующая работа с поставщиком привела к уменьшению изменчивости металлической вставки. Позже неслучайные причины изменчивости развились в процессе пластиковой формовки; это было немедленно выявлено с помощью контрольных карт и исправлено. Затем было выяснено, что можно без существенных потерь уменьшить число измеряемых деталей с 5 каждый час до пяти каждые 4 часа; впоследствии стало достаточно только пяти измерений каждые 8 часов.
Эта пластиковая формовочная операция была продолжена прерывающимися интервалами по 2 или 3 дня, разделенными несколькими неделями. Техника контрольных карт оказалась весьма полезной при контроле процесса для такого типа операции.
Некоторые комментарии к примеру В этом примере представлена ситуация, противоположная описанной в предыдущем примере и дана дальнейшая иллюстрация применений контрольных карт для переменных: В этом примере инженер по контролю качества использовал контрольные карты как естественное средство для диагностики нарушений производственного процесса. В ситуации, когда контрольные карты не используются, и наблюдается 31%-й уровень несоответствия продукции заданным спецификациям, руководство, зачастую необоснованно резко, повышает требования к качеству работы службы производственного надзора. Использование контрольных карт позволяет более гибким образом строить управленческие стратегии в отношении нарушений качества, потому что они дают инспекторам по надзору ключ к выявлению повседневных нарушений производственного процесса. Однако в этом случае первым сообщением контрольной карты для руководства будет то, что не надо делать. Карта говорит: “Не оказывайте давления на службу надзора”, а также “Не ищите причин ежечасной или ежедневной изменчивости”. В этой ситуации существуют три альтернативы: (a) произвести коренные изменения процесса, (b) изменить спецификации или (c) смириться с необходимостью продолжать отбор изделий, удовлетворяющих техническим условиям, с помощью 100%-го контроля. В этом случае границы допуска задаются произвольно без учета необходимости приведения их в соответствие. Следовательно, наиболее уместным является пересмотр спецификаций. В ситуации, описанной в данном примере, программа статистического контроля качества была введена в эксплуатацию. Это входило в обязанности инженера по контролю качества, который отчитывался непосредственно перед управляющим. Весьма выгодной является такая организационная структура, в которой существуют специальные отделы, занимающиеся обработкой информации, полученной при анализе контрольных карт, а также принятием соответствующих решений. Сопоставление этого примера с предыдущим подчеркивает тот факт, что статистический контроль является выражением, которое описывает скорее характер изменчивости процесса, чем его способность отвечать заданным спецификациям. В предыдущем примере 25% выборок показывали выход из-под контроля (выборки 9, 10, 12, 13 и 18), тогда как только 1% исследуемой продукции не удовлетворяет заданным спецификациям (одна деталь в 8-й выборке). В этом примере, несмотря на то, что все выборки находятся под контролем, 31% продукции не отвечает заданным требованиям. В предыдущем примере было отмечено, что указание границ допуска на карте средних (


Учебник по контролю качества (II)
  |
||||||||||||||||||||
и  Среди инструментов для контроля качества одним из самых мощных для диагностики производственных процессов является контрольная карта Шуэрта для переменных. Обычно курс по статистическому контролю качества начинается с краткого введения, посвященного этой контрольной карте. Одним из наших слушателей был технолог качества продукции на заводе, который ранее никогда не применял никакие статистические методы контроля качества. После прослушивания 2-х часовой лекции этот технолог для большего знакомства с контрольными картами создал экспериментальное приложение, использующее контрольную карту для одной операции в цехе. Операция заключалась в подгоночной шлифовке отверстий для гидравлической системы самолетов. Требуемый диаметр отверстий определялся 0.4037 ± 0.0013 дюйма. Результаты подгонки подвергаются затем проверке с помощью специального измерительного оборудования по принципу “годен – не годен”. Эта проверка обычно производится спустя несколько дней после выпуска контролируемого образца. В целях минимизации ошибок проверочной операции производственный отдел стремился добиться как можно большего соответствия среднего значения диаметра изделий номинальной величине 0.4037 дюйма. Для осуществления измерений с точностью до десятитысячных долей дюйма инспектор приобрел визуальный компаратор, который использовался для других целей. Примерно раз в час производилось измерение диаметра отверстий на пяти произведенных деталях. Для каждой выборки из пяти деталей вычислялись среднее и размах (разность между наибольшим и наименьшим значением в выборке). Таблица 1 содержит полученные результаты (Вы можете скачать файл данных в формате STATISTICA здесь). Таблица 1Таблица 1
Таблица 1. Измерения диаметров отверстий (Указаны значения отклонений в 0.0001 дюйма от величины 0.4000) Две карты, не являющиеся контрольными картами Если бы измерения были произведены до знакомства инспектора с методикой контрольных карт, вероятнее всего, были бы вычислены средние для каждой выборки, а размахи не были бы приняты во внимание. На Рисунках 1 и 2 показаны два типа карт, которые не являются контрольными картами, хотя и дают информацию такого же рода. Эти карты могут быть полезными для инспектора, но они не осуществляют функции, присущие контрольным картам. На Рисунке 1 показаны отдельные измерения, сгруппированные по выборкам. Также показаны номинальное значение и верхняя/нижняя граница доверительного интервала. Все измерения, кроме одного в 8-й выборке, лежат внутри доверительного интервала. На Рисунке 2 показаны средние этих выборок. Карта такого типа дает лучшее представление о тренде, чем карта на Рисунке 1. Но без границ, устанавливаемых с помощью методики Шуэрта, она не может указать на выход процесса из-под контроля в статистическом понимании контроля.  Рисунок 1. Диаметры отверстий: исходные измерения  Рисунок 2. Диаметры отверстий: средние выборок Необходимо отметить, что на Рисунке 2 показаны средние вместо отдельных значений, и было бы неверным указывать на этом рисунке те же самые границы доверительного интервала. Попадание в доверительный интервал может указываться только для отдельных наблюдений, а не для средних по выборкам. Выборочные средние часто попадают внутрь доверительного интервала даже в том случае, когда некоторые наблюдения лежат вне границ допуска. Это верно для 8-й выборки, среднее которой лежит близко к номинальному значению, несмотря на то, что одно наблюдение в этой выборке находится вне границ допуска. Следовательно, карта средних значений с указанными границами допуска вкладывает неверный смысл в утверждение о соблюдении процессом границ доверительного интервала. Две контрольные карты На Рисунке 3 показана контрольная    Рисунок 3. Диаметры отверстий:  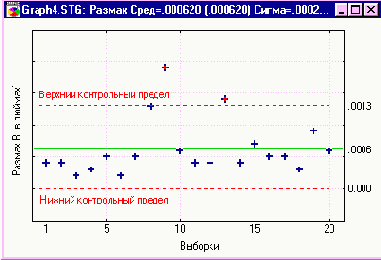 Рисунок 4. Диаметры отверстий:  На каждой из этих контрольных карт сплошная линия обозначает среднее значение. Общее среднее  На каждой карте также показаны две пунктирные линии, обозначенные как верхний контрольный предел и нижний контрольный предел. Расстояния от контрольных пределов до линии среднего значения зависит от размера выборки и среднего размаха  На  На  Карты показывают потерю контроля Три точки (выборки 10, 12 и 18) лежат вне контрольных пределов на карте средних. Две точки (выборки 9 и 13) лежат вне контрольных пределов на карте размаха. Это свидетельствует о том, что существуют неслучайные причины изменчивости в производственном процессе, т.е. такие факторы, воздействующие на качество продукции, которые должны быть выявлены и скорректированы. Конечно, ничего не может быть сделано с этими неслучайными причинами, так как контрольные пределы не установлены после 20-й точки. Контрольные карты на Рисунках 3 и 4 просто свидетельствуют о том, что существует возможность уменьшить изменчивость процесса. Контрольные карты приносят пользу при применении построенных контрольных пределов к производимой продукции. Сигнал о необходимости поиска неслучайных причин разладки процесса в момент выхода точки за контрольные пределы дает возможность для своевременного выявления этих причин. Действия по устранению этих причин могут состоять не только в устранении текущих неполадок, но и в предупреждении их появления в будущем. Указанная выше ситуация выхода из-под контроля будет очевидной для инспектора качества продукции, который составил подобную карту. Продолжение использования карты дает возможность установления неслучайных причин изменчивости среднего, в основном связанных с настройками машин, и неслучайных причин изменчивости размаха, обычно связанных с невнимательностью отдельного оператора. Усилия по предупреждению повторений подобных ситуаций приводят к существенному повышению качества продукта. Другие выводы из контрольных карт Простота контрольных карт подтверждается тем фактом, что описанный бдительный технолог оказался способен выгодно использовать карты после прослушивания только 6-ти часовой лекции по статистическому контролю качества, из которых только два часа было посвящено построению контрольных карт   Этот технолог успешно применил карты для контроля процессов, т.е. выявления и устранения неслучайных причин изменчивости качества. Тем не менее, для него могли оказаться скрытыми некоторые выводы, которые возможно сделать на основе более профессионального анализа карт. Эти выводы, несомненно, будут понятны тем, кто имеет дополнительные знания и опыт по этому вопросу: Если есть возможность осуществлять контроль (в статистическом смысле), естественный допуск такого процесса был бы примерно равен ± 0.0006 дюймов. Таким образом, при осуществлении статистического контроля будет несложно выдерживать заданные границы ± 0.0013 дюймов. Так как на практике среднее процесса оказалось несколько ниже номинала 0.4037 дюйма для минимизации износа измерительных приборов при 100% контроле датчиками по принципу “годен – не годен”, возникает вопрос, на каком уровне следует центрировать процесс. Если может быть осуществлен статистический контроль, этот уровень не должен быть ниже, чем 0.4030 дюйма для гарантии того, чтобы практически все изделия находились внутри границ допуска. Фактически для наших наблюдений среднее равно 0.4034 дюйма. Это было бы несомненно, если бы процесс мог удовлетворять статистическому контролю. Но для процесса, выходящего из-под контроля, всегда существует опасность брака вне зависимости от уставноленного уровня. Всякий раз, когда естественный допуск лежит внутри заданного допуска, внимание должно быть уделено целесообразности 100% контроля или замены его выборочным контролем с использованием контрольных карт. В этом случае пять измерений фактических размеров с заданными интервалами могут заменить 100% контроль датчиками по принципу “годен – не годен”, за исключением случаев, когда контрольная карта показывает выход из-под контроля. Такая замена не была бы произведена до тех пор, пока контрольные карты, примененные к этому процессу, показывали бы попадание всех точек внутрь контрольных пределов. Если такая замена произведена, исчезнут мотивы для уменьшения износа датчиков, и может быть достигнут уровень 0.4037. Некоторые комментарии к примеру Так как менеджеры на производстве иногда изначально имеют не совсем точное представление о статистическом контроле качества, стоит сделать несколько пояснений для большего понимания предмета. Неправильно полагают, что статистические методы могут применяться только для длительных периодов. Вследствие этого считается, что они не могут быть применимыми к новым операциям, которые длятся только несколько месяцев. Нужно отметить, что для полного понимания этого факта необходимо около 20 часов лекций. Так как в реальной действительности последние данные редко подходят для наиболее эффективного использования контрольных карт для переменных, обычно необходимо начинать поиск требуемых данных после решения об использовании этой методики. Время, необходимое для получения достаточной информации для принятия решения о необходимости каких-либо действий, зависит от длительности производства достаточного для соответствующей карты количества продукции. Другим неверным утверждением является то, что эти методы непременно используют сложную математику. На самом деле они основаны на простой арифметике и доступны на самом нижнем уровне управления производства. Распространено заблуждение, что эта методика считается настолько трудной для понимания, что она не может быть использована простым рабочим или контролирующим персоналом. Как уже отмечалось, нашему инспектору понадобилось только 2 часа инструктажа для хорошего понимания данной технологии. При этом не предполагалось, что 2 часа вполне достаточно для полного разъяснения контрольных карт для переменных; имелось в виду только то, что существенные особенности этой методологии могут быть объяснены за короткое время. Выше отмечалось также, что этот инспектор может не суметь на основе данных сделать некоторые выводы, которые, возможно, оказались бы для него полезными. Чем больше на предприятии несущих ответственность за организацию лиц, понимающих основы статистического контроля, и чем лучше они понимают его, тем больше возможностей для снижения издержек. Также неверно считать, что эта методика находит хорошее применение только тогда, когда вы осознаете, что у вас имеются определенного рода нарушения. Верно то, что одной из причин осознания трудностей является забота о создании наиболее благоприятных возможностей для снижения издержек. На самом деле эта методика повышает возможность снижения издержек и в том случае, когда нет осведомленности о нарушениях. Подтверждением этому в нашем примере служит возможность замены выборочного контроля 100%-м контролем качественных характеристик. Инспектор предпочитает эту частную операцию в некоторой степени случайно для обеспечения возможности эксперимента с методиками. Другое серьезное заблуждение заключается в утверждении, что эффективное использование методики статистического контроля качества может быть достигнуто только путем применения его в цехе. В примере было отмечено, что данные, сохраненные инспектором по продукции, указывают на возможность снижения издержек контроля. Системы бюджетного контроля в промышленности обычно идут по пути выдачи кредита для снижения издержек цеху определенного инспектора, но не для снижения в других цехах. В этом частном случае, если принимается решение установить приемочный статистический контроль по количественным признакам на месте производства с использованием контрольных карт в производственном цехе для контроля процесса и для приемки, возникает вопрос о том, какой персонал – производственный или контролирующий – будет осуществлять измерения. Этот вопрос должен решаться на управленческом уровне как производства, так и контроля. Если, как это обычно бывает на практике, принимается решение о целесообразности проведения измерений производственным персоналом, внешне это приводит к повышению издержек в производственном цехе. Может показаться, что увеличились издержки, за которые нес ответственность инспектор по продукции и уменьшились издержки в месте, где - это вопрос бюджетного порядка – инспектор не получил кредит. Очевидно, что без полного понимания высшим руководством, инспекторами по продукции и инспекторами по контролю того, как с помощью статистического контроля качества может быть достигнуто снижение издержек, рутинные операции системы бюджетного контроля могут фактически оказаться препятствием для сбережения средств. |
Учебник по контролю качества (III)


“Статистические методы служат своеобразным путеводителем, указывающим технологам на возможность развития, улучшения или повышения качества выпускаемой продукции. Эти рекомендации носят столь радикальный характер, что являются неожиданными даже для технических специалистов, посвященных во все тайны производиства.
Следовательно, после всех очевидных настроек производства, когда нормальная логика говорит, что дальнейшие улучшения невозможны, статистические методы указывают на возможность дальнейших улучшений. Таким образом, они заставляют человека, осуществляющего поиск неисправностей и достаточно уверенного в своих убеждениях, продолжать свою работу для достижения максимального улучшения вопреки определенному мнению, что такого улучшения нельзя никаким образом достичь.”
G. J. Meyers, Jr.
Использование контрольных карт для выявления случайных причин в стабильной системеНа основе контрольных карт



Эти вопросы могут быть выражены в разных терминах, например: “Из одного или разных источников произведены выборки?” или “Существует одна универсальная генеральная совокупность, из которых они берутся?” или “Свидетельствуют ли эти карты о стабильном характере изменчивости?” или “Является ли эта изменчивость результатом комплекса постоянно действующих причин?” или просто “Удовлетворяют ли данные измерения требованиям статистического контроля?”
Любое решающее правило, которое приводит к выбору “Да” или “Нет”, отсекает возможность противоположного ответа. Решение о том, где провести демаркационную линию между решениями “Да” и “Нет” основывается на ожидаемых действиях при каждом ответе на этот вопрос.
В контроле качества решение: “Нет, это не комплекс постоянно действующих факторов” приведет к поиску специальных причин, вызвавших изменчивость качества, и попыткам их устранения, если это возможно.
Ответ: “Да, это комплекс постоянно действующих факторов” приведет к тому, что процесс будет оставлен сам по себе, и не будут прилагаться усилия по поиску причин изменчивости.
Иными словами, мы ищем ответ на вопрос: происходит повышение изменчивости вследствие специфических производственных обстоятельств или изменчивость обусловлена постоянно действующими производственными факторами.
Правило определения контрольных пределов, которое определяется ответом “Да” и “Нет”, в любом случае приводит к проблеме баланса издержек, вызванных ошибками двух типов – ошибкой поиска неисправности, когда на самом деле она отсутствует (когда на самом деле имеет место: “Да”) и ошибкой отказа от поиска неисправности и оставления процесса без контроля в то время как такая неисправность реально существует (верен ответ: “Нет”).
Конечно, любое правило для установления контрольных пределов должно быть практическим правилом. Общепринятой практикой является использование пределов 3-сигма. Опыт свидетельствует, что в большинстве случаев пределы 3-сигма позволяют проводить удовлетворительное разграничение этих двух типов ошибок. (Несмотря на то, что, в принципе, выбор пределов является проблемой минимизации суммы определенных издержек, это одна из самых больших практических трудностей при построении хороших оценок релевантных издержек).
Устойчивая и неустойчивая изменчивость На Рисунке 1 представлен график частотного распределения массы содержимого 260 консервных банок с томатом, которые наблюдались в течение 11-дневного периода. На первый взгляд может показаться, что это распределение говорит об удовлетворительном характере изменчивости на протяжении 11 дней.
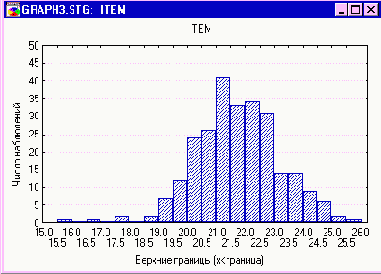
Рисунок 1
Это утверждение не обязательно является верным. Может случиться так, что характер изменчивости претерпевает некоторые изменения в течение этого периода. Первый вопрос, на который должен быть дан ответ – является ли этот характер стабильным. Если очевидно отсутствие стабильности, это может означать, что 260 наблюдений представляют собой выборки из различных генеральных совокупностей, существующих в различные моменты времени. В этом случае полученное частотное распределение будет представлять собой взвешенное среднее по различным генеральным совокупностям, которые изменяются от выборки к выборке.
Всякий раз, когда частотное распределение используется в качестве основы для оценки возможностей производственного процесса, или вносятся преднамеренные изменения в процесс, или пересматриваются спецификации, контрольные карты становятся важным инструментом для выявления стабильности. Если обнаруживается, что процесс стабилен, аналитик может утверждать с достаточной степенью надежности, что измеряется одна генеральная совокупность, а не взвешенное среднее многих. Порядок, в котором производятся измерения, был бы всегда сохранен в учетных данных для плотности распределения.
Использование контрольных карт для интерпретации частотного распределения На Рисунках 2 и 3 показаны контрольные карты




Таблица 1
Таблица 1
| Номер выборки | Измерение каждой банки (по пять деталей в час) |
Среднее |
Размах |
||||
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 |
22.0 20.5 20.0 21.0 22.5 23.0 19.0 21.5 21.0 21.5 20.0 19.0 19.5 20.0 22.5 21.5 19.0 21.0 20.0 22.0 19.0 21.5 22.5 22.5 18.5 21.5 24.0 19.5 22.0 22.0 22.5 20.0 21.0 22.5 22.0 25.0 20.5 21.5 21.5 22.5 21.5 23.0 22.5 23.5 21.0 24.5 24.0 23.5 22.0 22.0 23.5 24.5 |
22.5 22.5 20.5 22.0 19.5 23.5 20.0 20.5 22.5 23.0 19.5 21.0 20.5 21.5 19.5 20.5 21.5 20.5 23.5 20.5 20.5 25.0 22.0 22.0 22.0 20.5 22.0 22.5 17.5 20.0 21.0 22.0 19.5 21.5 21.0 20.0 21.0 22.0 22.0 24.5 24.0 23.5 19.5 23.0 21.0 21.5 21.0 22.5 20.5 23.5 21.0 21.5 |
22.5 22.5 23.0 22.0 22.5 21.0 22.0 19.0 20.0 22.0 21.0 21.0 21.0 24.0 21.0 22.0 23.0 19.5 24.0 21.0 21.0 21.0 23.0 22.0 22.5 20.5 17.5 15.5 21.0 20.5 19.5 20.0 22.0 21.0 21.0 20.0 21.0 22.0 21.5 25.5 21.5 21.0 21.5 24.5 24.5 21.5 24.0 20.0 21.0 24.0 23.5 21.0 |
24.0 23.0 22.0 23.0 22.0 22.0 20.5 19.5 22.0 23.0 20.0 21.0 20.5 23.0 21.5 21.5 21.0 22.0 20.5 22.5 20.5 19.0 22.0 19.5 21.0 16.5 21.0 20.0 22.0 24.0 21.5 21.5 20.0 21.5 20.5 20.5 19.0 20.0 20.5 20.0 21.5 21.5 20.5 21.5 23.0 22.5 22.0 20.0 22.5 22.0 21.5 24.5 |
23.5 21.5 21.5 22.0 21.0 20.0 22.5 19.5 22.0 18.5 20.5 20.5 21.0 20.0 21.0 23.5 23.5 21.0 21.5 20.0 22.5 21.0 23.5 20.5 21.5 21.5 22.5 22.5 23.5 21.5 22.5 20.0 20.0 23.5 21.0 22.5 21.0 21.0 22.5 21.0 22.5 21.5 20.0 20.5 22.5 22.5 20.5 21.0 23.0 22.0 23.0 22.5 |
22.9 22.0 21.4 22.0 21.5 21.9 20.8 20.0 21.5 21.6 20.2 20.5 20.5 21.7 21.1 21.8 21.6 20.8 21.9 21.2 20.7 21.5 22.6 21.3 21.1 20.1 21.4 20.0 21.2 21.6 21.4 20.7 20.5 22.0 21.1 21.6 20.5 21.3 21.6 22.7 22.2 22.1 20.8 22.6 22.4 22.5 22.3 21.4 21.8 22.7 22.5 22.8 |
2.0 2.5 3.0 2.0 3.0 3.5 3.5 2.5 2.5 4.5 1.5 2.0 1.5 4.0 3.0 3.0 4.5 2.5 4.0 2.5 3.5 6.0 1.5 3.0 4.0 5.0 6.5 7.0 6.0 4.0 3.0 2.0 2.5 2.5 1.5 5.0 2.0 2.0 2.0 5.5 2.5 2.5 3.0 4.0 3.5 3.0 3.5 3.5 2.5 2.0 2.5 3.5 |
Таблица 1. Масса консервных банок после их заполнения
(в унциях)
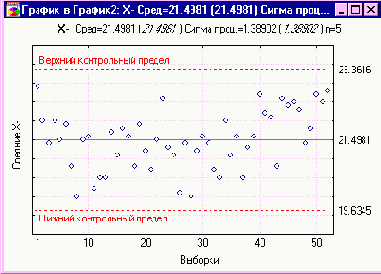
Рисунок 2
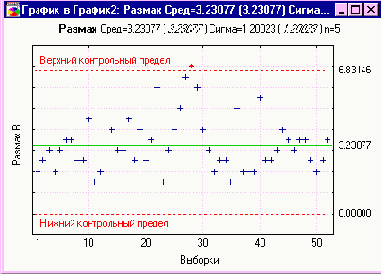
Рисунок 3
-карта для выборок из нормального резервуара Шуэрта Распределение значений

Отсюда следует, что если в длинной последовательности измерений выборки являются нормальными и произведены из одной генеральной совокупности, то их средние почти всегда попадают внутрь интервала m ± 3s

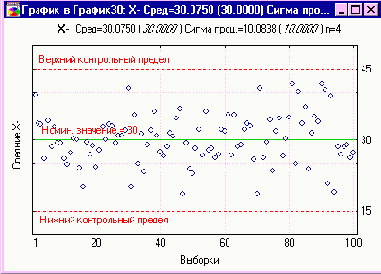
Рисунок 4
Таблица 2
Таблица 2
| Измерения | Среднее |
Размах R |
Стд. откл. s |
|||
| 47 33 34 12 35 19 23 33 25 29 40 21 26 52 26 19 28 29 21 24 28 41 14 32 42 20 30 28 35 51 34 32 14 25 18 21 17 36 25 35 21 39 40 23 23 36 35 33 18 23 7 29 36 36 38 11 31 22 29 42 29 23 34 27 34 39 42 30 43 17 40 22 30 41 5 38 27 20 29 25 42 24 38 22 46 27 31 32 35 55 22 14 36 29 33 52 23 28 32 23 |
32 33 34 21 23 37 45 12 22 32 18 18 35 29 20 1 34 25 37 22 39 32 23 28 34 38 14 29 30 13 19 28 31 44 22 31 44 48 31 21 22 22 44 25 37 52 23 15 30 30 32 30 12 37 9 44 18 47 24 26 40 22 27 40 38 19 25 25 22 31 49 39 36 37 20 26 38 23 29 35 59 32 40 52 32 29 26 46 20 25 46 24 52 21 31 34 41 22 27 23 |
44 34 31 24 38 31 26 29 37 30 30 36 31 21 30 30 39 24 32 16 23 46 41 46 22 27 37 32 37 45 11 41 20 29 20 39 54 19 38 20 44 24 24 46 44 30 11 40 22 20 36 39 34 39 25 29 31 12 32 32 43 23 52 23 16 39 25 38 10 10 38 26 34 27 43 38 40 28 34 37 38 22 31 33 20 24 34 30 34 33 52 2 19 17 32 17 21 45 16 27 |
35 34 34 47 40 27 37 43 33 13 11 34 29 18 20 30 17 30 25 35 21 12 42 27 34 32 43 35 26 55 16 40 35 27 33 25 13 41 30 34 19 29 18 29 34 28 5 29 25 19 38 31 25 32 39 29 25 27 44 27 29 39 28 24 28 32 42 39 28 16 37 18 18 32 26 25 33 35 29 42 28 22 52 27 50 15 35 32 46 54 42 43 50 9 18 5 29 21 30 36 |
39.50 33.50 33.25 26.00 34.00 28.50 32.75 29.25 29.25 26.00 24.75 27.25 30.25 30.00 24.00 20.00 29.50 27.00 28.75 24.25 27.75 32.75 30.00 33.25 33.00 29.25 31.00 31.00 32.00 41.00 20.00 35.25 25.00 31.25 23.25 29.00 32.00 36.00 31.00 27.50 26.50 28.50 31.50 30.75 34.50 36.50 18.50 29.25 23.75 23.00 28.25 32.25 26.75 36.00 27.75 28.25 26.25 27.00 32.25 31.75 35.25 26.75 35.25 28.50 29.00 32.25 33.50 33.00 25.75 18.50 41.00 26.25 29.50 34.25 23.50 31.75 34.50 26.50 30.25 34.75 41.75 25.00 40.25 33.50 37.00 23.75 31.50 35.00 33.75 41.75 40.50 20.75 39.25 19.00 28.50 27.00 28.50 29.00 26.25 27.25 |
15 1 3 35 17 18 22 31 15 19 29 18 9 34 10 29 22 6 16 19 18 34 28 19 20 18 29 7 11 42 23 13 21 19 15 18 41 29 13 15 25 17 26 23 21 24 30 25 12 11 31 10 24 7 30 33 13 35 20 16 14 17 25 17 22 20 17 14 33 21 12 21 18 14 38 13 13 15 5 17 31 10 21 30 30 14 9 16 26 30 30 41 33 20 15 47 20 24 16 13 |
7.1 0.6 1.5 14.9 7.6 7.5 10.1 12.9 6.9 8.8 12.8 9.1 3.8 15.4 4.9 13.7 9.5 2.9 7.1 7.9 8.1 15.0 13.8 8.8 8.2 7.6 12.5 3.2 5.0 19.1 9.9 6.3 9.7 8.7 6.7 7.8 20.1 12.4 5.4 8.1 11.7 7.6 12.5 10.5 8.7 10.9 13.3 10.5 5.1 5.0 14.4 4.6 10.9 2.9 14.0 13.5 6.2 14.7 8.5 7.3 7.3 8.2 11.6 7.9 9.6 9.4 9.8 6.7 13.7 8.9 5.5 9.1 8.1 6.1 15.7 7.2 5.8 6.6 2.5 7.1 12.9 4.8 8.7 13.1 13.7 6.2 4.0 7.4 10.7 15.1 13.0 17.3 15.3 8.3 7.0 20.5 9.0 11.1 7.1 6.1 |
Таблица 2. 400 измерений из нормального резервуара Шуэрта,
объединенные в выборки по 4
На Рисунок 4 центральная линия могла быть установлена в значение 30, равное m , известному значению среднего генеральной совокупности. Пределы 3-сигма могли быть вычислены на основе известного значения s, стандартного отклонения резервуара, которое округленно равно 10. Стандартная ошибка среднего равна
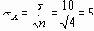
Следовательно, границы 3-сигма отстояли на величину 3s

Неверно утверждать, что для длинной серии, при условии неизменности генеральной совокупности, за границы 3-сигма на



Тем не менее, такое неверное указание на отсутствие контроля встречается нечасто. Границы 3-сигма редко дают ошибку при обнаружении нарушения (т.е. обнаружении неслучайных причин изменчивости), когда на самом деле нарушений не происходит. Если точки на

Вычисление границ 3-сигма для контрольных



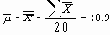
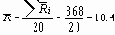
Далее оценивается s с помощью Таблицы 6. Для этого нужно определить из Таблицы 6 значение фактора d2 для данного размера выборок. В нашем случае n = 4, и Таблица 6 дает d2 = 2.059.
Оценка s,
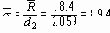
Теперь 3s


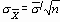
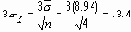
Верхний контрольный предел


Нижний контрольный предел

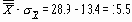
Эти два шага вычисления 3s

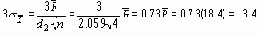
Для облегчения вычислений контрольных пределов по

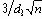


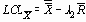
Если контрольные пределы вычисляются не по




Далее используется значение c4 из Таблицы 6.
Оценка s,
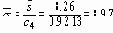

Где

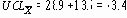

Как и при вычислении по


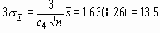
Для облегчения вычислений контрольных пределов по


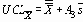
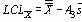
Для тех ситуаций, когда желательно вычислять контрольные пределы прямо по известным стандартным значениям s и m , множитель
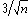
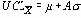
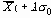
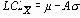
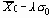
По этим формулам были вычислены контрольные пределы для контрольной карты на рисунке 4. В данном случае для известных значений m = 30 и s = 10 значение для A в Таблице 9 равно 1.50 и
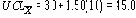
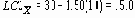
Различные уравнения для центральной линии и контрольных границ 3-сигма на контрольных картах для








В промышленной практике в большинстве случаев границы вычисляются по

Таблица 3
Таблица 3
| Метод |  |
R-карта | s-карта |
| m и s известны или предполагаемы (X0, s 0) | 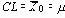 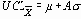 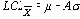 таблица 9 |
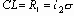   таблицы 6 и 9 |
   таблицы 6 и 9 |
m и s
оценены по   |
 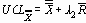 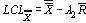 таблица 7 |
 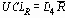  таблица 7 |
|
m и s
оценены по   |
   таблица 8 |
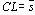  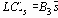 таблица 8 |
контрольных пределов 3-сигма (CL - центральная линия)
Контрольные карты размаха и стандартное отклонение выборки Основной формулой для контрольных пределов на

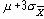

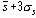
На Рисунках 5 и 6 показаны контрольные карты R и s для 100 выборок по четыре, представленных в Таблице 2. Пределы на этих картах вычислены с использованием соответствующих значений




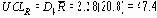
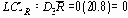
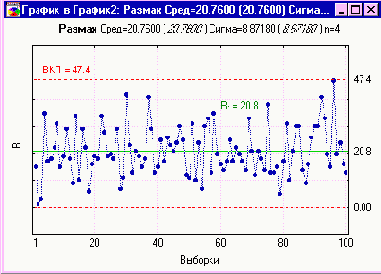
Рисунок 5

Рисунок 6
Сходство изменчивости от выборки к выборке на R и s картах становится заметным при проведении линии, последовательно соединяющей все точки. Кажется очевидным, что обе карты показывают одинаковую историю. Каждая из них может быть использована для отображения истории процесса; нет необходимости использовать сразу обе.
Обычно в качестве меры разброса используется R, хотя время от времени используется s. Целью проведения вычислений как R, так и s для данных в Таблице 2 было показать, что R и s являются альтернативными измерениями одной и той же характеристики, что они приводят к сходным оценкам s, сходным контрольным пределам для

При практическом использовании контрольных карт в промышленности для измерения разброса выборок намного чаще используется R, а не s.
Как уже было сказано, такой выбор делается вследствие простоты вычисления R с помощью ручных расчетов. Также важно то преимущество, что R более просто для понимания; почти каждый может понять смысл размахов, тогда как люди со слабым знанием статистики с трудом понимают смысл стандартного отклонения.
Оценки s по







Если образцы выбираются один за другим из резервуара Шуэрта и каждый образец возвращается и образцы перемешиваются перед очередным взятием выборки, не существует некоторого естественного размера выборок; допустимо объединять образцы в выборки любого размера. Для иллюстрации эффекта различия в объеме выборок 400 отобранных образцов были разбиты на выборки по 2, 4, а затем по 8 образцов в выборке, и для каждой выборки были вычислены значения R и s. Значения




В Таблице 4 показаны оценки s для каждого набора по 80 образцов и для всех 400 образцов с использованием статистик




Размах выборки размера 2 равен





Таблица 4
Таблица 4
| Наблю- дения |
Оценки s | |||||
| Выборки по 2 | Выборки по 4 | Выборки по 8 | ||||
По  |
По  |
По  |
По  |
По  |
По  |
|
| 1-80 81-160 161-240 241-320 321-400 |
8.62 10.75 9.73 8.86 11.68 |
8.62 10.75 9.73 8.86 11.68 |
8.94 10.51 10.51 8.89 11.56 |
8.97 10.64 10.48 9.06 11.48 |
9.24 10.50 9.76 8.85 11.98 |
8.98 10.58 9.89 9.02 12.17 |
| 1-400 | 9.93 | 9.93 | 10.08 | 10.12 | 10.07 | 10.13 |
генеральной совокупности s по выборкам размера 2,4 и 8
(известное значение s = 9.95)
Несмотря на то, что достаточно хорошие оценки s могут быть получены по различным выборкам разного размера, в конкретных случаях часто имеются основания для выбора определенного размера выборки.
Распределение стандартного отклонения Gen Leslie Simon в начале своей презентации по выборочному контролю по количественным признакам привел следующую цитату из DeMorgan “A Budget of Paradoxes”:
Большие блохи съедают маленьких,
И маленькие – еще меньших, и так до бесконечности.
Был ли прав DeMorgan или нет насчет блох, но эта идея, несомненно, проводит параллель с теорией распределений в математической статистике. Генеральные совокупности позволяют строить распределения, имеющие меньший разброс, такие как распределение средних, стандартных отклонений или размахов. И если каждая генеральная совокупность имеет свое среднее и стандартное отклонение, то каждое распределение средних, стандартных отклонений или размахов имеет собственное среднее и стандартное отклонение.
К сожалению, статистическая теория не может дать нам такие полезные обобщения распределения s, как это делается для


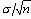

Также утверждается, что, даже если распределение генеральной совокупности не является нормальным, распределение значений

Несмотря на это, если генеральная совокупность нормальна, статистическая теория может дать нам ожидаемое среднее и ожидаемое стандартное отклонение распределения s. Как уже было отмечено, в выборках из нормальной генеральной совокупности ожидаемое среднее

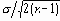
Теоретические знания о распределении s для выборок из нормальной совокупности позволяют строить 3-сигма границы на контрольных s-картах. Центральная линия на контрольной карте устанавливается на уровне

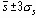
Приблизительное значение ss для нормальной совокупности равно

Современная статистическая теория дает точное значение, равное
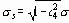
Когда n велико, разность между (1) и (2) незначительна. Уравнение (2) используется для вычисления контрольных пределов, когда n равно или меньше 25; уравнение (1) используется при n, большем 25.
Когда границы 3-сигма для




Когда пределы основаны на известном или предполагаемом значении стандартного отклонения генеральной совокупности s, они равны
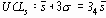
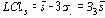
При вычислении ss для множителей B4 и B3, приведенных в Таблице 8, s полагается равной
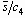
Распределение размахов Несмотря на то, что не существует простой формулы для вычисления как ожидаемого среднего размаха R, так и для стандартного отклонения размаха sR, статистическая теория дает отношение этих величин к стандартному отклонению s для нормальной генеральной совокупности. Теория также полностью определяет ожидаемое распределение R выборок из нормальной генеральной совокупности.
Когда 3- сигма пределы вычисляются по наблюдаемому R, они равны
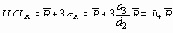
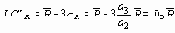
Когда пределы основаны на известном или предполагаемом значении стандартного отклонения s, они равны
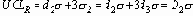
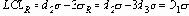
В этих формулах множитель d2 численно выражает ожидаемое значение


Модификация множителя d2 для малого числа выборок При оценке s по


Строго говоря, обоснованное применение точного значения множителя d2 предполагает что размахи усреднены по достаточно хорошему количеству выборок, скажем, 20 или больше. В случае, когда доступно небольшое количество выборок, наилучшая оценка s получается при использовании множителя, который обычно обозначается как

Таблица 5
Таблица 5
| Число выборок по 5 |  |
Число выборок по 5 |  |
| 1 | 2.474 | 8 | 2.346 |
| 2 | 2.405 | 10 | 2.342 |
| 3 | 2.379 | 12 | 2.339 |
| 5 | 2.358 | 20 | 2.334 |
| 6 | 2.353 | бесконечность | 2.326 |


для различных размеров выборок по 5
из нормальной генеральной совокупности
Обычно при построении контрольных карт для контроля качества в промышленности для практических целей больше подходят множители, основанные на d2, а не на


Роль контрольных карт в устранении причин неполадок Контрольные карты для переменных являются руководством к различного рода действиям. Некоторые из этих действий, в частности, связанные со спецификациями и допусками и с процедурой приемки, основываются на уверенности в том, что процесс находится под контролем.
Для таких действий хорошо было бы понять свойства систем с комплексом постоянно действующих причин.
Другие полезные действия основываются на предположении, что процесс не находится под контролем. Примером служит поиск неисправностей в производственном процессе. Такие контрольные карты в одних случаях говорят: “Предоставьте этот процесс самому себе”, а в других – “Ищите неисправность и попробуйте устранить ее”.
Боле полезным свойством контрольных карт является то, что они говорят – в разумных пределах – когда нужно искать причины изменчивости. Всегда полезно знать этот момент; иногда это может быть полезно для выявления того, где нужно проводить поиск. Знание этого значительно облегчает сложную работу с момента принятия решения о поиске неисправности до фактического обнаружения и устранения причин неполадок. Этот факт лежит в основе известного утверждения H.F.Dodge: “Статистический контроль качества - это на 90% инженерное дело и на 10% - статистика”.
Контрольные карты сами по себе не могут точно указывать, где может быть найдена причина неисправности. Тем не менее, пользователи метода контрольных карт иногда развивают способность диагностики причин с поразительной точностью. Такие возможности обычно зависят от понимания принципов контрольных карт в сочетании с хорошими знаниями конкретных технологических процессов, к которым применяются контрольные карты.
Не существует общей книги по статистическому контролю качества, которая описывала бы все возможные технологические процессы. Тем не менее, может быть создано руководство по статистическим аспектам интерпретации контрольных карт для поиска и устранения неисправностей. Мы можем попытаться предоставить такое руководство путем обследования некоторых общих случаев, в которых может произойти выход из-под контроля и указания эффективности каждого применения контрольных карт


Выход из-под контроля означает сдвиг в генеральной совокупности Метод выборки фишек из резервуара является полезной аналогией в разъяснении, что реально происходит, когда производственный процесс выходит из-под контроля.
Система случайных причин в каждый момент времени соответствует выборке, то есть распределению фишек в резервуаре. Изделия, фактически производимые в эти моменты, соответствуют выборкам, произведенным из этого резервуара или, иными словами, из этой генеральной совокупности. Когда точки выходят за пределы на контрольных картах, становится очевидным, что генеральная совокупность подверглась изменениям; это соответствует тому, что выборки были сделаны из различных резервуаров.
Обычно изделия, произведенные в какой-либо период времени, образуют выборку из генеральной совокупности, большую, чем изделия, фактически измеренные в течение того же самого периода для учета контрольными картами. Таким образом, контрольные карты предоставляют факты не только относительно генеральной совокупности (то есть системы случайных причин), но и относительно произведенных изделий, которые не были измерены.
Классификация состояний, в которых может возникнуть выход из-под контроля Поскольку отсутствие контроля соответствует случаю изменения резервуара, классификация различных типов отсутствия контроля может пониматься как классификация состояний, в которых два резервуара отличаются распределением вероятностей фишек. Полезно отдельно рассматривать три случая, в которых генеральные совокупности: могут различаться только по среднему; могут различаться только по дисперсии; могут различаться по среднему и по дисперсии. Сдвиги по среднему генеральной совокупности отображаются на контрольных картах


Сдвиги в генеральной совокупности могут продолжаться в течение длительного времени, как если производится изъятие большого числа выборок из одного резервуара и затем значительно большее число выбирается из другого резервуара. Или сдвиги могут быть частыми и нерегулярными как если существует значительное число резервуаров с выборками, произведенными из каждого резервуара в течение различных периодов времени. Или сдвиги могут быть последовательными и систематическими.
На Рисунке 7 частотная кривая описывает генеральную совокупность, или резервуар, то есть комплекс случайных причин по операциям в любой момент времени. Рисунок 7-a показывает ситуацию, в которой генеральная совокупность имеет постоянное среднее, затем происходит сдвиг в сторону увеличения, а в конце среднее падает до начального значения. Рисунок 7-b показывает ситуацию, в которой среднее генеральной совокупности неустойчиво, а дисперсия генеральной совокупности остается постоянной. На Рисунке 7-c среднее генеральной совокупности постепенно увеличивается. Рисунок 7-d показывает ситуацию, в которой, несмотря на то, что среднее генеральной совокупности остается неизменным, дисперсия генеральной совокупности удваивается. Рисунок 7-e представляет генеральную совокупность с непостоянными средним и дисперсией.
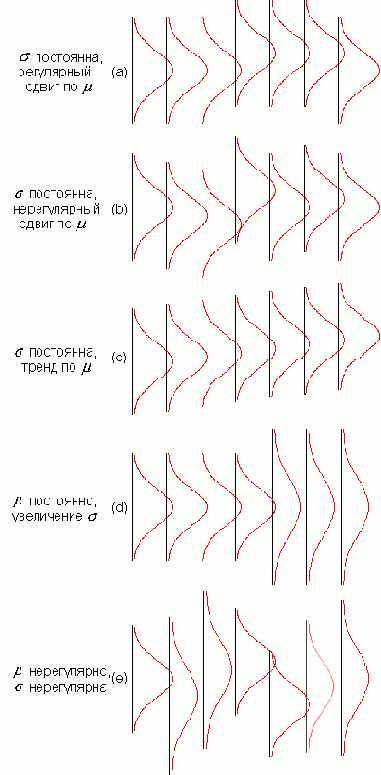
Рисунок 7
Изменения среднего генеральной совокупности На производстве чаще всего наблюдается такая ситуация выхода из-под контроля, когда происходит сдвиг среднего генеральной совокупности, а ее дисперсия почти не изменяется. В таких случаях контрольные карты являются весьма ценными для настройщика машин, так как помогают ему производить регулировку механизмов для достижения желательного среднего процесса. Этот тип выхода из-под контроля регистрируется контрольными


В тех случаях, когда контрольные карты используются для выявления изменений среднего генеральной совокупности, соответствующая схема отбора выборок отличается от случаев, когда контрольные карты служат нескольким целям, включая приемочный контроль.
Так как, как объяснялось ранее, контрольные пределы устанавливаются достаточно от центральной линии на карте для того чтобы меньше точек лежало за пределами без реальных изменений в генеральной совокупности, малые сдвиги среднего генеральной совокупности не являются причинами выхода большого числа точек из-под контроля.
Для этих целей часто полезно дополнить данные, полученные положением точек относительно контрольных пределов данными, полученными с помощью тестов, основанными на статистической теории серий или последовательностей.
Приложение Таблица 6
Таблица 6
| Число наблюдений в выборке, n | Множитель d2, |
Множитель d3, |
Множитель c2, |
Множитель c4,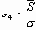 |
| 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 30 35 40 45 50 55 60 65 70 75 80 85 90 95 100 |
1.128 1.693 2.059 2.326 2.534 2.704 2.847 2.970 3.078 3.173 3.258 3.336 3.407 3.472 3.532 3.588 3.640 3.689 3.735 3.778 3.819 3.858 3.895 3.931 4.086 4.213 4.322 4.415 4.498 4.572 4.639 4.699 4.755 4.806 4.854 4.898 4.939 4.978 5.015 |
0.8525 0.8884 0.8798 0.8641 0.8480 0.8332 0.8198 0.8078 0.7971 0.7873 0.7785 0.7704 0.7630 0.7562 0.7499 0.7441 0.7386 0.7335 0.7287 0.7242 0.7199 0.7159 0.7121 0.7084 0.6926 0.6799 0.6692 0.6601 0.6521 0.6452 0.6389 0.6337 0.6283 0.6236 0.6194 0.6154 0.6118 0.6084 0.6052 |
0.5642 0.7236 0.7979 0.8407 0.8686 0.8882 0.9027 0.9139 0.9227 0.9300 0.9359 0.9410 0.9453 0.9490 0.9523 0.9551 0.9576 0.9599 0.9619 0.9638 0.9655 0.9670 0.9684 0.9696 0.9748 0.9784 0.9811 0.9832 0.9849 0.9863 0.9874 0.9884 0.9892 0.9900 0.9906 0.9912 0.9916 0.9921 0.9925 |
0.7979 0.8862 0.9213 0.9400 0.9515 0.9594 0.9650 0.9693 0.9727 0.9754 0.9776 0.9794 0.9810 0.9823 0.9835 0.9845 0.9854 0.9862 0.9869 0.9876 0.9882 0.9887 0.9892 0.9896 0.9914 0.9927 0.9936 0.9943 0.9949 0.9954 0.9958 0.9961 0.9964 0.9966 0.9968 0.9970 0.9972 0.9973 0.9975 |





Все множители вычислены при предположении о нормальности генеральной совокупности
Таблица 7
Таблица 7
| Число наблюдений в выборке, n | Множитель для  A2 |
Множители для R карт | |
| НКП D3 |
ВКП D4 |
||
| 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
1.88 1.02 0.73 0.58 0.48 0.42 0.37 0.34 0.31 0.29 0.27 0.25 0.24 0.22 0.21 0.20 0.19 0.19 0.18 |
0 0 0 0 0 0.08 0.14 0.18 0.22 0.26 0.28 0.31 0.33 0.35 0.36 0.38 0.39 0.40 0.41 |
3.27 2.57 2.28 2.11 2.00 1.92 1.86 1.82 1.78 1.74 1.72 1.69 1.67 1.65 1.64 1.62 1.61 1.60 1.59 |
Таблица 7. Множители для определения по

контрольных пределов 3-сигма для

Верхний контрольный предел для
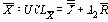
Нижний контрольный предел для

Верхний контрольный предел для

Нижний контрольный предел для
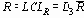
Все множители в таблице основаны на нормальном распределении
Таблица 8
Таблица 8
| Число наблюдений в выборке, N | Множитель для  с использованием  A1 |
Множитель для  с использованием  A3 |
Множители для s и s rms карт | |
| НКП B3 |
ВКП B4 |
|||
| 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 30 35 40 45 50 55 60 65 70 75 80 85 90 95 100 |
3.76 2.39 1.88 1.60 1.41 1.28 1.17 1.09 1.03 0.97 0.93 0.88 0.85 0.82 0.79 0.76 0.74 0.72 0.70 0.68 0.66 0.65 0.63 0.62 0.56 0.52 0.48 0.45 0.43 0.41 0.39 0.38 0.36 0.35 0.34 0.33 0.32 0.31 0.30 |
2.66 1.95 1.63 1.43 1.29 1.18 1.10 1.03 0.98 0.93 0.89 0.85 0.82 0.79 0.76 0.74 0.72 0.70 0.68 0.66 0.65 0.63 0.62 0.61 0.55 0.51 0.48 0.45 0.43 0.41 0.39 0.37 0.36 0.35 0.34 0.33 0.32 0.31 0.30 |
0 0 0 0 0.03 0.12 0.19 0.24 0.28 0.32 0.35 0.38 0.41 0.43 0.45 0.47 0.48 0.50 0.51 0.52 0.53 0.54 0.55 0.56 0.60 0.63 0.66 0.68 0.70 0.71 0.72 0.73 0.74 0.75 0.76 0.77 0.77 0.78 0.79 |
3.27 2.57 2.27 2.09 1.97 1.88 1.81 1.76 1.72 1.68 1.65 1.62 1.59 1.57 1.55 1.53 1.52 1.50 1.49 1.48 1.47 1.46 1.45 1.44 1.40 1.37 1.34 1.32 1.30 1.29 1.28 1.27 1.26 1.25 1.24 1.23 1.23 1.22 1.21 |

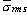
контрольных пределов 3-сигма для

Верхний контрольный предел для

Нижний контрольный предел для
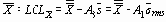
Верхний контрольный предел для s и
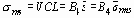
Нижний контрольный предел для s и

Все множители в таблице основаны на нормальном распределении
Таблица 9
Таблица 9
| Число наблюдений в выборке, n | Множители для A |
Множители для R карт | Множители для s rms карт | Множители для s карт | |||
| НКП D1 |
ВКП D2 |
НКП B1 |
ВКП B2 |
НКП B5 |
ВКП B6 |
||
| 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 30 35 40 45 50 55 60 65 70 75 80 85 90 95 100 |
2.12 1.73 1.50 1.34 1.22 1.13 1.06 1.00 0.95 0.90 0.87 0.83 0.80 0.77 0.75 0.73 0.71 0.69 0.67 0.65 0.64 0.63 0.61 0.60 0.55 0.51 0.47 0.45 0.42 0.40 0.39 0.37 0.36 0.35 0.34 0.33 0.32 0.31 0.30 |
0 0 0 0 0 0.20 0.39 0.55 0.69 0.81 0.92 1.03 1.12 1.21 1.28 1.36 1.43 1.49 1.55 |
3.69 4.36 4.70 4.92 5.08 5.20 5.31 5.39 5.47 5.53 5.59 5.65 5.69 5.74 5.78 5.82 5.85 5.89 5.92 |
0 0 0 0 0.03 0.10 0.17 0.22 0.26 0.30 0.33 0.36 0.38 0.41 0.43 0.44 0.46 0.48 0.49 0.50 0.52 0.53 0.54 0.55 0.59 0.62 0.65 0.67 0.68 0.70 0.71 0.72 0.74 0.75 0.75 0.76 0.77 0.77 0.78 |
1.84 1.86 1.81 1.76 1.71 1.67 1.64 1.61 1.58 1.56 1.54 1.52 1.51 1.49 1.48 1.47 1.45 1.44 1.43 1.42 1.41 1.41 1.40 1.39 1.36 1.33 1.31 1.30 1.28 1.27 1.26 1.25 1.24 1.23 1.23 1.22 1.22 1.21 1.20 |
0 0 0 0 0.03 0.11 0.18 0.23 0.28 0.31 0.35 0.37 0.40 0.42 0.44 0.46 0.48 0.49 0.50 0.52 0.53 0.54 0.55 0.56 0.60 0.63 0.66 0.68 0.69 0.71 0.72 0.73 0.74 0.75 0.76 0.77 0.77 0.78 0.78 |
2.61 2.28 2.09 1.96 1.87 1.81 1.75 1.71 1.67 1.64 1.61 1.59 1.56 1.54 1.53 1.51 1.50 1.48 1.47 1.46 1.45 1.44 1.43 1.42 1.38 1.36 1.33 1.31 1.30 1.28 1.27 1.26 1.25 1.24 1.24 1.23 1.22 1.22 1.21 |
Таблица 9. Множители для определения по s
контрольных пределов 3-сигма для

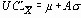
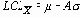
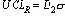
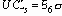

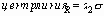
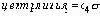

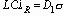


Элементарные понятия статистики
Элементарные понятия статистики
Обзор элементарных понятий статистики. Это введение представляет собой краткое обсуждение элементарных понятий, лежащих в основе любой процедуры статистического анализа данных. Мы выбрали темы, которые иллюстрируют основные предположения большинства статистических методов, предназначенных для понимания "численной природы" действительности (Nisbett, et al., 1987). Мы сосредотачиваем основное внимание на "функциональных" аспектах обсуждаемых понятий, прекрасно понимая, что предлагаемое описание является кратким и не может исчерпать всего предмета обсуждения. Более подробную информацию можно найти во вводных разделах и разделах примеров руководства пользователя системы STATISTICA, а также в учебниках по статистике. Мы рекомендуем следующие учебники: Kachigan (1986) и Runyon and Haber (1976); для углубленного обсуждения элементарной теории и основных понятий статистики см. классическую книгу Kendall and Stuart (1979) (перевод: М.Кендалл и А.Стьюарт "Теория распределений" (том 1), "Статистические выводы и связи" (том 2), "Многомерный статистический анализ" (том 3)). На русском языке см., например, книгу: Боровиков В.П. "Популярное введение в программу STATISTICA", Компьютер Пресс 1998, в которой дается популярное описание основных статистических понятий.
Что такое переменные? Переменные - это то, что можно измерять, контролировать или что можно изменять в исследованиях. Переменные отличаются многими аспектами, особенно той ролью, которую они играют в исследованиях, шкалой измерения и т.д.
Исследование зависимостей в сравнении с экспериментальными исследованиями. Большинство эмпирических исследований данных можно отнести к одному из названных типов. В исследовании корреляций (зависимостей, связей...) вы не влияете (или, по крайней мере, пытаетесь не влиять) на переменные, а только измеряете их и хотите найти зависимости (корреляции) между некоторыми измеренными переменными, например, между кровяным давлением и уровнем холестерина.
В экспериментальных исследованиях, напротив, вы варьируете некоторые переменные и измеряете воздействия этих изменений на другие переменные. Например, исследователь может искусственно увеличивать кровяное давление, а затем на определенных уровнях давления измерить уровень холестерина. Анализ данных в экспериментальном исследовании также приходит к вычислению "корреляций" (зависимостей) между переменными, а именно, между переменными, на которые воздействуют, и переменными, на которые влияет это воздействие. Тем не менее, экспериментальные данные потенциально снабжают нас более качественной информацией. Только экспериментально можно убедительно доказать причинную связь между переменными. Например, если обнаружено, что всякий раз, когда изменяется переменная A, изменяется и переменная B, то можно сделать вывод - "переменная A оказывает влияние на переменную B", т.е. между переменными А и В имеется причинная зависимость. Результаты корреляционного исследования могут быть проинтерпретированы в каузальных (причинных) терминах на основе некоторой теории, но сами по себе не могут отчетливо доказать причинность.
Зависимые и независимые переменные. Независимыми переменными называются переменные, которые варьируются исследователем, тогда как зависимые переменные - это переменные, которые измеряются или регистрируются. Может показаться, что проведение этого различия создает путаницу в терминологии, поскольку как говорят некоторые студенты "все переменные зависят от чего-нибудь". Тем не менее, однажды отчетливо проведя это различие, вы поймете его необходимость. Термины зависимая и независимая переменная применяются в основном в экспериментальном исследовании, где экспериментатор манипулирует некоторыми переменными, и в этом смысле они "независимы" от реакций, свойств, намерений и т.д. присущих объектам исследования. Некоторые другие переменные, как предполагается, должны "зависеть" от действий экспериментатора или от экспериментальных условий.
Иными словами, зависимость проявляется в ответной реакции исследуемого объекта на посланное на него воздействие. Отчасти в противоречии с данным разграничением понятий находится использование их в исследованиях, где вы не варьируете независимые переменные, а только приписываете объекты к "экспериментальным группам", основываясь на некоторых их априорных свойствах. Например, если в эксперименте мужчины сравниваются с женщинами относительно числа лейкоцитов (WCC), содержащихся в крови, то Пол можно назвать независимой переменной, а WCC зависимой переменной.
Шкалы измерений. Переменные различаются также тем "насколько хорошо" они могут быть измерены или, другими словами, как много измеряемой информации обеспечивает шкала их измерений. Очевидно, в каждом измерении присутствует некоторая ошибка, определяющая границы "количества информации", которое можно получить в данном измерении. Другим фактором, определяющим количество информации, содержащейся в переменной, является тип шкалы, в которой проведено измерение. Различают следующие типы шкал:(a) номинальная, (b) порядковая (ординальная), (c) интервальная (d) относительная (шкала отношения). Соответственно, имеем четыре типа переменных: (a) номинальная, (b) порядковая (ординальная), (c) интервальная и (d) относительная. Номинальные переменные используются только для качественной классификации. Это означает, что данные переменные могут быть измерены только в терминах принадлежности к некоторым, существенно различным классам; при этом вы не сможете определить количество или упорядочить эти классы. Например, вы сможете сказать, что 2 индивидуума различимы в терминах переменной А (например, индивидуумы принадлежат к разным национальностям). Типичные примеры номинальных переменных - пол, национальность, цвет, город и т.д. Часто номинальные переменные называют категориальными. Порядковые переменные позволяют ранжировать (упорядочить) объекты, указав какие из них в большей или меньшей степени обладают качеством, выраженным данной переменной.
Однако они не позволяют сказать "на сколько больше" или "на сколько меньше". Порядковые переменные иногда также называют ординальными. Типичный пример порядковой переменной - социоэкономический статус семьи. Мы понимаем, что верхний средний уровень выше среднего уровня, однако сказать, что разница между ними равна, скажем, 18% мы не сможем. Само расположение шкал в следующем порядке: номинальная, порядковая, интервальная является хорошим примером порядковой шкалы. Интервальные переменные позволяют не только упорядочивать объекты измерения, но и численно выразить и сравнить различия между ними. Например, температура, измеренная в градусах Фаренгейта или Цельсия, образует интервальную шкалу. Вы можете не только сказать, что температура 40 градусов выше, чем температура 30 градусов, но и что увеличение температуры с 20 до 40 градусов вдвое больше увеличения температуры от 30 до 40 градусов. Относительные переменные очень похожи на интервальные переменные. В дополнение ко всем свойствам переменных, измеренных в интервальной шкале, их характерной чертой является наличие определенной точки абсолютного нуля, таким образом, для этих переменных являются обоснованными предложения типа: x в два раза больше, чем y. Типичными примерами шкал отношений являются измерения времени или пространства. Например, температура по Кельвину образует шкалу отношения, и вы можете не только утверждать, что температура 200 градусов выше, чем 100 градусов, но и что она вдвое выше. Интервальные шкалы (например, шкала Цельсия) не обладают данным свойством шкалы отношения. Заметим, что в большинстве статистических процедур не делается различия между свойствами интервальных шкал и шкал отношения.
Связи между переменными. Независимо от типа, две или более переменных связаны (зависимы) между собой, если наблюдаемые значения этих переменных распределены согласованным образом. Другими словами, мы говорим, что переменные зависимы, если их значения систематическим образом согласованы друг с другом в имеющихся у нас наблюдениях.
Например, переменные Пол и WCC ( число лейкоцитов) могли бы рассматриваться как зависимые, если бы большинство мужчин имело высокий уровень WCC, а большинство женщин - низкий WCC, или наоборот. Рост связан с Весом, потому что обычно высокие индивиды тяжелее низких; IQ (коэффициент интеллекта) связан с Количеством ошибок в тесте, т.к. люди высоким значением IQ делают меньше ошибок и т.д.
Почему зависимости между переменными являются важными. Вообще говоря, конечная цель всякого исследования или научного анализа состоит в нахождение связей (зависимостей) между переменными. Философия науки учит, что не существует иного способа представления знания, кроме как в терминах зависимостей между количествами или качествами, выраженными какими-либо переменными. Таким образом, развитие науки всегда заключается в нахождении новых связей между переменными. Исследование корреляций по существу состоит в измерении таких зависимостей непосредственным образом. Тем не менее, экспериментальное исследование не является в этом смысле чем-то отличным. Например, отмеченное выше экспериментальное сравнение WCC у мужчин и женщин может быть описано как поиск связи между переменными: Пол и WCC. Назначение статистики состоит в том, чтобы помочь объективно оценить зависимости между переменными. Действительно, все сотни описанных в данном руководстве процедур могут быть проинтерпретированы в терминах оценки различных типов взаимосвязей между переменными.
Две основные черты всякой зависимости между переменными. Можно отметить два самых простых свойства зависимости между переменными: (a) величина зависимости и (b) надежность зависимости. Величина. Величину зависимости легче понять и измерить, чем надежность. Например, если любой мужчина в вашей выборке имел значение WCC выше чем любая женщина, то вы можете сказать, что зависимость между двумя переменными (Пол и WCC) очень высокая. Другими словами, вы могли бы предсказать значения одной переменной по значениям другой. Надежность ("истинность").
Надежность взаимозависимости - менее наглядное понятие, чем величина зависимости, однако чрезвычайно важное. Надежность зависимости непосредственно связана с репрезентативностью определенной выборки, на основе которой строятся выводы. Другими словами, надежность говорит нам о том, насколько вероятно, что зависимость, подобная найденной вами, будет вновь обнаружена (иными словами, подтвердится) на данных другой выборки, извлеченной из той же самой популяции. Следует помнить, что конечной целью почти никогда не является изучение данной конкретной выборки; выборка представляет интерес лишь постольку, поскольку она дает информацию обо всей популяции. Если ваше исследование удовлетворяет некоторым специальным критериям (об этом будет сказано позже), то надежность найденных зависимостей между переменными вашей выборки можно количественно оценить и представить с помощью стандартной статистической меры (называемой p-уровень или статистический уровень значимости, подробнее см. в следующем разделе).
Что такое статистическая значимость (p-уровень)? Статистическая значимость результата представляет собой оцененную меру уверенности в его "истинности" (в смысле "репрезентативности выборки"). Выражаясь более технически, p-уровень (этот термин был впервые использован в работе Brownlee, 1960) это показатель, находящийся в убывающей зависимости от надежности результата. Более высокий p- уровень соответствует более низкому уровню доверия к найденной в выборке зависимости между переменными. Именно, p-уровень представляет собой вероятность ошибки, связанной с распространением наблюдаемого результата на всю популяцию. Например, p- уровень = .05 (т.е. 1/20) показывает, что имеется 5% вероятность, что найденная в выборке связь между переменными является лишь случайной особенностью данной выборки. Иными словами, если данная зависимость в популяции отсутствует, а вы многократно проводили бы подобные эксперименты, то примерно в одном из двадцати повторений эксперимента можно было бы ожидать такой же или более сильной зависимости между переменными. (Отметим, что это не то же самое, что утверждать о заведомом наличии зависимости между переменными, которая в среднем может быть воспроизведена в 5% или 95% случаев; когда между переменными популяции существует зависимость, вероятность повторения результатов исследования, показывающих наличие этой зависимости называется плана.
Подробнее об этом см. в разделе ). Во многих исследованиях p-уровень .05 рассматривается как "приемлемая граница" уровня ошибки.
Как определить, является ли результат действительно значимым. Не существует никакого способа избежать произвола при принятии решения о том, какой уровень значимости следует действительно считать "значимым". Выбор определенного уровня значимости, выше которого результаты отвергаются как ложные, является достаточно произвольным. На практике окончательное решение обычно зависит от того, был ли результат предсказан априори (т.е. до проведения опыта) или обнаружен апостериорно в результате многих анализов и сравнений, выполненных с множеством данных, а также на традиции, имеющейся в данной области исследований. Обычно во многих областях результат p




Статистическая значимость и количество выполненных анализов. Понятно, что чем больше число анализов вы проведете с совокупностью собранных данных, тем большее число значимых (на выбранном уровне) результатов будет обнаружено чисто случайно. Например, если вы вычисляете корреляции между 10 переменными (имеете 45 различных коэффициентов корреляции), то можно ожидать, что примерно два коэффициента корреляции (один на каждые 20) чисто случайно окажутся значимыми на уровне p

Тем не менее, многие статистические методы (особенно простые методы разведочного анализа данных) не предлагают какого-либо способа решения данной проблемы. Поэтому исследователь должен с осторожностью оценивать надежность неожиданных результатов.
Величина зависимости между переменными в сравнении с надежностью зависимости. Как было уже сказано, величина зависимости и надежность представляют две различные характеристики зависимостей между переменными. Тем не менее, нельзя сказать, что они совершенно независимы. Говоря общим языком, чем больше величина зависимости (связи) между переменными в выборке обычного объема, тем более она надежна (см. следующий раздел).
Почему более сильные зависимости между переменными являются более значимыми. Если предполагать отсутствие зависимости между соответствующими переменными в популяции, то наиболее вероятно ожидать, что в исследуемой выборке связь между этими переменными также будет отсутствовать. Таким образом, чем более сильная зависимость обнаружена в выборке, тем менее вероятно, что этой зависимости нет в популяции, из которой она извлечена. Как вы видите, величина зависимости и значимость тесно связаны между собой, и можно было бы попытаться вывести значимость из величины зависимости и наоборот. Однако указанная связь между зависимостью и значимостью имеет место только при фиксированном объеме выборки, поскольку при различных объемах выборки одна и та же зависимость может оказаться как высоко значимой, так и незначимой вовсе (см. следующий раздел)
Почему объем выборки влияет на значимость зависимости. Если наблюдений мало, то соответственно имеется мало возможных комбинаций значений этих переменных и таким образом, вероятность случайного обнаружения комбинации значений, показывающих сильную зависимость, относительно велика. Рассмотрим следующий пример. Если вы исследуете зависимость двух переменных (Пол: мужчина/женщина и WCC: высокий/низкий) и имеете только 4 субъекта в выборке (2 мужчины и 2 женщины), то вероятность того, что чисто случайно вы найдете 100% зависимость между двумя переменными равна 1/8.
Более точно, вероятность того, что оба мужчины имеют высокий WCC, а обе женщины - низкий WCC, или наоборот, - равна 1/8. Теперь рассмотрим вероятность подобного совпадения для 100 субъектов; легко видеть, что эта вероятность равна практически нулю. Рассмотрим более общий пример. Представим популяцию, в которой среднее значение WCC мужчин и женщин одно и тоже. Если вы будете повторять эксперимент, состоящий в извлечении пары случайных выборок (одна выборка - мужчины, другая выборка - женщины), а затем вычислите разности выборочных средних WCC для каждой пары выборок, то в большинстве экспериментов результат будет близок к 0. Однако время от времени, будут встречаться пары выборок, в которых различие между средним количеством лейкоцитов у мужчин и женщин будет существенно отличаться от 0. Как часто это будет происходить? Очевидно, чем меньше объем выборки в каждом эксперименте, тем более вероятно появление таких ложных результатов, которые показывают существование зависимости между полом и WCC в данных, полученных из популяции, где такая зависимость на самом деле отсутствует.
Пример: "отношение числа новорожденных мальчиков к числу новорожденных девочек" Рассмотрим следующий пример, заимствованный из Nisbett, et al., 1987. Имеются 2 больницы. Предположим, что в первой из них ежедневно рождается 120 детей, во второй только 12. В среднем отношение числа мальчиков, рождающихся в каждой больнице, к числу девочек 50/50. Однажды девочек родилось вдвое больше, чем мальчиков. Спрашивается, для какой больницы данное событие более вероятно? Ответ очевиден для статистика, однако, он не столь очевиден неискушенному. Конечно, такое событие гораздо более вероятно для маленькой больницы. Объяснение этого факта состоит в том, что вероятность случайного отклонения (от среднего) возрастает с уменьшением объема выборки.
Почему слабые связи могут быть значимо доказаны только на больших выборках. Пример из предыдущего раздела показывает, что если связь между переменными "объективно" слабая (т.е.
свойства выборки близки к свойствам популяции), то не существует иного способа проверить такую зависимость кроме как исследовать выборку достаточно большого объема. Даже если выборка, находящаяся в вашем распоряжении, совершенно репрезентативна, эффект не будет статистически значимым, если выборка мала. Аналогично, если зависимость "объективно" (в популяции) очень сильная, тогда она может быть обнаружена с высокой степенью значимости даже на очень маленькой выборке. Рассмотрим пример. Представьте, что вы бросаете монету. Если монета слегка несимметрична, и при подбрасывании орел выпадает чаще решки (например, в 60% подбрасываний выпадает орел, а в 40% решка), то 10 подбрасываний монеты было бы не достаточно, чтобы убедить кого бы то ни было, что монета асимметрична, даже если был бы получен, казалось, совершенно репрезентативный результат: 6 орлов и 4 решки. Не следует ли отсюда, что 10 подбрасываний вообще не могут доказать что-либо? Нет, не следует, потому что если эффект, в принципе, очень сильный, то 10 подбрасываний может оказаться вполне достаточно для его доказательства. Представьте, что монета настолько несимметрична, что всякий раз, когда вы ее бросаете, выпадает орел. Если вы бросаете такую монету 10 раз, и всякий раз выпадает орел, большинство людей сочтут это убедительным доказательством того, что с монетой что-то не то. Другими словами, это послужило бы убедительным доказательством того, что в популяции, состоящей из бесконечного числа подбрасываний этой монеты орел будет встречаться чаще, чем решка. В итоге этих рассуждений мы приходим к выводу: если зависимость сильная, она может быть обнаружена с высоким уровнем значимости даже на малой выборке.
Можно ли отсутствие связей рассматривать как значимый результат? Чем слабее зависимость между переменными, тем большего объема требуется выборка, чтобы значимо ее обнаружить. Представьте, как много бросков монеты необходимо сделать, чтобы доказать, что отклонение от равной вероятности выпадения орла и решки составляет только .000001%! Необходимый минимальный размер выборки возрастает, когда степень эффекта, который нужно доказать, убывает.
Когда эффект близок к 0, необходимый объем выборки для его отчетливого доказательства приближается к бесконечности. Другими словами, если зависимость между переменными почти отсутствует, объем выборки, необходимый для значимого обнаружения зависимости, почти равен объему всей популяции, который предполагается бесконечным. Статистическая значимость представляет вероятность того, что подобный результат был бы получен при проверке всей популяции в целом. Таким образом, все, что получено после тестирования всей популяции было бы, по определению, значимым на наивысшем, возможном уровне и это относится ко всем результатам типа "нет зависимости".
Как измерить величину зависимости между переменными. Статистиками разработано много различных мер взаимосвязи между переменными. Выбор определенной меры в конкретном исследовании зависит от числа переменных, используемых шкал измерения, природы зависимостей и т.д. Большинство этих мер, тем не менее, подчиняются общему принципу: они пытаются оценить наблюдаемую зависимость, сравнивая ее с "максимальной мыслимой зависимостью" между рассматриваемыми переменными. Говоря технически, обычный способ выполнить такие оценки заключается в том, чтобы посмотреть как варьируются значения переменных и затем подсчитать, какую часть всей имеющейся вариации можно объяснить наличием "общей" ("совместной") вариации двух (или более) переменных. Говоря менее техническим языком, вы сравниваете то "что есть общего в этих переменных", с тем "что потенциально было бы у них общего, если бы переменные были абсолютно зависимы". Рассмотрим простой пример. Пусть в вашей выборке, средний показатель (число лейкоцитов) WCC равен 100 для мужчин и 102 для женщин. Следовательно, вы могли бы сказать, что отклонение каждого индивидуального значения от общего среднего (101) содержит компоненту связанную с полом субъекта и средняя величина ее равна 1. Это значение, таким образом, представляет некоторую меру связи между переменными Пол и WCC.
Конечно, это очень бедная мера зависимости, так как она не дает никакой информации о том, насколько велика эта связь, скажем относительно общего изменения значений WCC. Рассмотрим крайние возможности: Если все значения WCC у мужчин были бы точно равны 100, а у женщин 102, то все отклонения значений от общего среднего в выборке всецело объяснялись бы полом индивидуума. Поэтому вы могли бы сказать, что пол абсолютно коррелирован (связан) с WCC, иными словами, 100% наблюдаемых различий между субъектами в значениях WCC объясняются полом субъектов. Если же значения WCC лежат в пределах 0-1000, то та же разность (2) между средними значениями WCC мужчин и женщин, обнаруженная в эксперименте, составляла бы столь малую долю общей вариации, что полученное различие (2) считалось бы пренебрежимо малым. Рассмотрение еще одного субъекта могло бы изменить разность или даже изменить ее знак. Поэтому всякая хорошая мера зависимости должна принимать во внимание полную изменчивость индивидуальных значений в выборке и оценивать зависимость по тому, насколько эта изменчивость объясняется изучаемой зависимостью.
Общая конструкция большинства статистических критериев. Так как конечная цель большинства статистических критериев (тестов) состоит в оценивании зависимости между переменными, большинство статистических тестов следуют общему принципу, объясненному в предыдущем разделе. Говоря техническим языком, эти тесты представляют собой отношение изменчивости, общей для рассматриваемых переменных, к полной изменчивости. Например, такой тест может представлять собой отношение той части изменчивости WCC, которая определяется полом, к полной изменчивости WCC (вычисленной для объединенной выборки мужчин и женщин). Это отношение обычно называется отношением объясненной вариации к полной вариации. В статистике термин объясненная вариация не обязательно означает, что вы даете ей "теоретическое объяснение". Он используется только для обозначения общей вариации рассматриваемых переменных, иными словами, для указания на то, что часть вариации одной переменной "объясняется" определенными значениями другой переменной и наоборот.
Как вычисляется уровень статистической значимости. Предположим, вы уже вычислили меру зависимости между двумя переменными (как объяснялось выше). Следующий вопрос, стоящий перед вами: "насколько значима эта зависимость?" Например, является ли 40% объясненной дисперсии между двумя переменными достаточным, чтобы считать зависимость значимой? Ответ: "в зависимости от обстоятельств". Именно, значимость зависит в основном от объема выборки. Как уже объяснялось, в очень больших выборках даже очень слабые зависимости между переменными будут значимыми, в то время как в малых выборках даже очень сильные зависимости не являются надежными. Таким образом, для того чтобы определить уровень статистической значимости, вам нужна функция, которая представляла бы зависимость между "величиной" и "значимостью" зависимости между переменными для каждого объема выборки. Данная функция указала бы вам точно "насколько вероятно получить зависимость данной величины (или больше) в выборке данного объема, в предположении, что в популяции такой зависимости нет". Другими словами, эта функция давала бы уровень значимости (p -уровень), и, следовательно, вероятность ошибочно отклонить предположение об отсутствии данной зависимости в популяции. Эта "альтернативная" гипотеза (состоящая в том, что нет зависимости в популяции) обычно называется нулевой гипотезой. Было бы идеально, если бы функция, вычисляющая вероятность ошибки, была линейной и имела только различные наклоны для разных объемов выборки. К сожалению, эта функция существенно более сложная и не всегда точно одна и та же. Тем не менее, в большинстве случаев ее форма известна, и ее можно использовать для определения уровней значимости при исследовании выборок заданного размера. Большинство этих функций связано с очень важным классом распределений, называемым нормальным.
Почему важно Нормальное распределение. Нормальное распределение важно по многим причинам. В большинстве случаев оно является хорошим приближением функций, определенных в предыдущем разделе (более подробное описание см.
в разделе ). Распределение многих статистик является нормальным или может быть получено из нормальных с помощью некоторых преобразований. Рассуждая философски, можно сказать, что нормальное распределение представляет собой одну из эмпирически проверенных истин относительно общей природы действительности и его положение может рассматриваться как один из фундаментальных законов природы. Точная форма нормального распределения (характерная "колоколообразная кривая") определяется только двумя параметрами: средним и стандартным отклонением.
Характерное свойство нормального распределения состоит в том, что 68% всех его наблюдений лежат в диапазоне ±1 стандартное отклонение от среднего, а диапазон ±2 стандартных отклонения содержит 95% значений. Другими словами, при нормальном распределении, стандартизованные наблюдения, меньшие -2 или большие +2, имеют относительную частоту менее 5% (Стандартизованное наблюдение означает, что из исходного значения вычтено среднее и результат поделен на стандартное отклонение (корень из дисперсии)). Если у вас имеется доступ к пакету STATISTICA, Вы можете вычислить точные значения вероятностей, связанных с различными значениями нормального распределения, используя Вероятностный калькулятор; например, если задать z-значение (т.е. значение случайной величины, имеющей стандартное нормальное распределение) равным 4, соответствующий вероятностный уровень, вычисленный STATISTICA будет меньше .0001, поскольку при нормальном распределении практически все наблюдения (т.е. более 99.99%) попадут в диапазон ±4 стандартных отклонения.
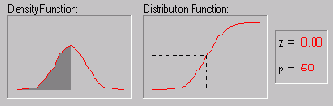
Иллюстрация того, как нормальное распределение используется в статистических рассуждениях (индукция). Напомним пример, обсуждавшийся выше, когда пары выборок мужчин и женщин выбирались из совокупности, в которой среднее значение WCC для мужчин и женщин было в точности одно и то же. Хотя наиболее вероятный результат таких экспериментов (одна пара выборок на эксперимент) состоит в том, что разность между средними WCC для мужчин и женщин для каждой пары близка к 0, время от время появляются пары выборок, в которых эта разность существенно отличается от 0.
Как часто это происходит? Если объем выборок достаточно большой, то разности "нормально распределены" и зная форму нормальной кривой, вы можете точно рассчитать вероятность случайного получения результатов, представляющих различные уровни отклонения среднего от 0 - значения гипотетического для всей популяции. Если вычисленная вероятность настолько мала, что удовлетворяет принятому заранее уровню значимости, то можно сделать лишь один вывод: ваш результат лучше описывает свойства популяции, чем "нулевая гипотеза". Следует помнить, что нулевая гипотеза рассматривается только по техническим соображениям как начальная точка, с которой сопоставляются эмпирические результаты. Отметим, что все это рассуждение основано на предположении о нормальности распределения этих повторных выборок (т.е. нормальности выборочного распределения). Это предположение обсуждается в следующем разделе.
Все ли статистики критериев нормально распределены? Не все, но большинство из них либо имеют нормальное распределение, либо имеют распределение, связанное с нормальным и вычисляемое на основе , такое как , или . Обычно эти критериальные статистики требуют, чтобы анализируемые переменные сами были нормально распределены в совокупности. Многие наблюдаемые переменные действительно нормально распределены, что является еще одним аргументом в пользу того, что нормальное распределение представляет "фундаментальный закон". Проблема может возникнуть, когда пытаются применить тесты, основанные на предположении нормальности, к данным, не являющимся нормальными (смотри критерии нормальности в разделах или ). В этих случаях вы можете выбрать одно из двух. Во-первых, вы можете использовать альтернативные "непараметрические" тесты (так называемые "свободно распределенные критерии", см. раздел Непараметрическая статистика и распределения). Однако это часто неудобно, потому что обычно эти критерии имеют меньшую мощность и обладают меньшей гибкостью. Как альтернативу, во многих случаях вы можете все же использовать тесты, основанные на предположении нормальности, если уверены, что объем выборки достаточно велик.
Последняя возможность основана на чрезвычайно важном принципе, позволяющем понять популярность тестов, основанных на нормальности. А именно, при возрастании объема выборки, форма выборочного распределения (т.е. распределение выборочной статистики критерия , этот термин был впервые использован в работе Фишера, Fisher 1928a) приближается к нормальной, даже если распределение исследуемых переменных не является нормальным. Этот принцип иллюстрируется следующим анимационным роликом, показывающим последовательность выборочных распределений (полученных для последовательности выборок возрастающего размера: 2, 5, 10, 15 и 30), соответствующих переменным с явно выраженным отклонением от нормальности, т.е. имеющих заметную асимметричность распределения.
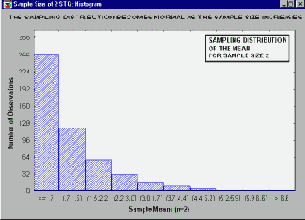
Однако по мере увеличения размера выборки, используемой для получения распределения выборочного среднего, это распределение приближается к нормальному. Отметим, что при размере выборки n=30, выборочное распределение "почти" нормально (см. на близость линии подгонки). Этот принцип называется центральной предельной теоремой (впервые этот термин был использован в работе Polya, 1920; по-немецки "Zentraler Grenzwertsatz").
Как узнать последствия нарушений предположений нормальности? Хотя многие утверждения других разделов Элементарных понятий статистики можно доказать математически, некоторые из них не имеют теоретического обоснования и могут быть продемонстрированы только эмпирически, с помощью так называемых экспериментов Moнте-Кaрло. В этих экспериментах большое число выборок генерируется на компьютере, а результаты полученные из этих выборок, анализируются с помощью различных тестов. Этим способом можно эмпирически оценить тип и величину ошибок или смещений, которые вы получаете, когда нарушаются определенные теоретические предположения тестов, используемых вами. Исследования с помощью методов Монте- Карло интенсивно использовались для того, чтобы оценить, насколько тесты, основанные на предположении нормальности, чувствительны к различным нарушениям предположений нормальности.Общий вывод этих исследований состоит в том, что последствия нарушения предположения нормальности менее фатальны, чем первоначально предполагалось. Хотя эти выводы не означают, что предположения нормальности можно игнорировать, они увеличили общую популярность тестов, основанных на нормальном распределении.

(c) Copyright StatSoft, Inc., 1984-2001
STATISTICA является торговой маркой StatSoft, Inc.
Список использованной литературы
Список использованной литературы
Abraham, B., & Ledolter, J. (1983). Statistical methods for forecasting. New York: Wiley.
Adorno, T. W., Frenkel-Brunswik, E., Levinson, D. J., & Sanford, R. N. (1950). The authoritarian personality. New York: Harper.
Agresti, Alan (1996). An Introduction to Categorical Data Analysis. New York: Wilely.
Akaike, H. (1973). Information theory and an extension of the maximum likelihood principle. In B. N. Petrov and F. Csaki (Eds.), Second International Symposium on Information Theory. Budapest: Akademiai Kiado.
Akaike, H. (1983). Information measures and model selection. Bulletin of the International Statistical Institute: Proceedings of the 44th Session, Volume 1. Pages 277-290.
Aldrich, J. H., & Nelson, F. D. (1984). Linear probability, logit, and probit models. Beverly Hills, CA: Sage Publications.
Almon, S. (1965). The distributed lag between capital appropriations and expenditures. Econometrica, 33, 178-196.
American Supplier Institute (1984-1988). Proceedings of Supplier Symposia on Taguchi Methods. (April, 1984; November, 1984; October, 1985; October, 1986; October, 1987; October, 1988), Dearborn, MI: American Supplier Institute.
Anderson, O. D. (1976). Time series analysis and forecasting. London: Butterworths.
Anderson, S. B., & Maier, M. H. (1963). 34,000 pupils and how they grew. Journal of Teacher Education, 14, 212-216.
Anderson, T. W. (1958). An introduction to multivariate statistical analysis. New York: Wiley.
Anderson, T. W., & Rubin, H. (1956). Statistical inference in factor analysis. Proceedings of the Third Berkeley Symposium on Mathematical Statistics and Probability. Berkeley: The University of California Press.
Andrews, D. F. (1972). Plots of high-dimensional data. Biometrics, 28, 125-136.
ASQC/AIAG (1990). Measurement systems analysis reference manual. Troy, MI: AIAG.
ASQC/AIAG (1991). Fundamental statistical process control reference manual. Troy, MI: AIAG.
AT&T (1956). Statistical quality control handbook, Select code 700-444. Indianapolis, AT&T Technologies.
Auble, D. (1953). Extended tables for the Mann- Whitney statistic. Bulletin of the Institute of Educational Research, Indiana University, 1, No. 2.
Bagozzi, R. P., & Yi, Y. (1989). On the use of structural equation models in experimental design. Journal of Marketing Research, 26, 271-284.
Bagozzi, R. P., Yi, Y., & Singh, S. (1991). On the use of structural equation models in experimental designs: Two extensions. International Journal of Research in Marketing, 8, 125-140.
Bails, D. G., & Peppers, L. C. (1982). Business fluctuations: Forecasting techniques and applications. Englewood Cliffs, NJ: Prentice-Hall.
Bailey, A. L. (1931). The analysis of covariance. Journal of the American Statistical Association, 26, 424-435.
Bain, L. J. (1978). Statistical analysis of reliability and life-testing models. New York: Decker.
Baird, J. C. (1970). Psychophysical analysis of visual space. New York: Pergamon Press.
Baird, J. C., & Noma, E. (1978). Fundamentals of scaling and psychophysics. New York: Wiley.
Barcikowski, R., & Stevens, J. P. (1975). A Monte Carlo study of the stability of canonical correlations, canonical weights, and canonical variate-variable correlations. Multivariate Behavioral Research, 10, 353-364.
Barker, T. B. (1986). Quality engineering by design: Taguchi's philosophy. Quality Progress, 19, 32-42.
Barlow, R. E., Marshall, A. W., & Proschan, F. (1963). Properties of probability distributions with monotone hazard rate. Annals of Mathematical Statistics, 34, 375-389.
Barlow, R. E., & Proschan, F. (1975). Statistical theory of reliability and life testing. New York: Holt, Rinehart, & Winston.
Barnard, G. A. (1959). Control charts and stochastic processes. Journal of the Royal Statistical Society, Ser. B, 21, 239.
Bartholomew, D. J. (1984). The foundations of factor analysis. Biometrika, 71, 221-232.
Bates, D. M., & Watts, D. G. (1988). Nonlinear regression analysis and its applications. New York: Wiley.
Bayne, C. K., & Rubin, I. B. (1986). Practical experimental designs and optimization methods for chemists. Deerfield Beach, FL: VCH Publishers.
Becker, R. A., Denby, L., McGill, R., & Wilks, A. R. (1986). Datacryptanalysis: A case study. Proceedings of the Section on Statistical Graphics, American Statistical Association, 92-97.
Belsley, D. A., Kuh, E., and Welsch, R. E. (1980). Regression Diagnostics. New York: Wiley.
Bendat, J. S. (1990). Nonlinear system analysis and identification from random data. New York: Wiley.
Bentler, P. M, & Bonett, D. G. (1980). Significance tests and goodness of fit in the analysis of covariance structures. Psychological Bulletin, 88, 588-606.
Bentler, P. M. (1986). Structural modeling and Psychometrika: A historical perspective on growth and achievements. Psychometrika, 51, 35-51.
Bentler, P. M. (1989). EQS Structural equations program manual. Los Angeles, CA: BMDP Statistical Software.
Bentler, P. M., & Weeks, D. G. (1979). Interrelations among models for the analysis of moment structures. Multivariate Behavioral Research, 14, 169-185.
Bentler, P. M., & Weeks, D. G. (1980). Linear structural equations with latent variables. Psychometrika, 45, 289-308.
Benzecri, J. P. (1973). L'Analyse des Donnees: T. 2, I' Analyse des correspondances. Paris: Dunod.
Berkson, J. (1944). Application of the Logistic Function to Bio-Assay. Journal of the American Statistical Association, 39, 357-365.
Berkson, J., & Gage, R. R. (1950). The calculation of survival rates for cancer. Proceedings of Staff Meetings, Mayo Clinic, 25, 250.
Bhote, K. R. (1988). World class quality. New York: AMA Membership Publications.
Binns, B., & Clark, N. (1986). The graphic designer's use of visual syntax. Proceedings of the Section on Statistical Graphics, American Statistical Association, 36-41.
Birnbaum, Z. W. (1952). Numerical tabulation of the distribution of Kolmogorov's statistic for finite sample values. Journal of the American Statistical Association, 47, 425-441.
Birnbaum, Z. W. (1953). Distribution- free tests of fit for continuous distribution functions. Annals of Mathematical Statistics, 24, 1-8.
Bishop, Y. M. M., Fienberg, S. E., & Holland, P. W. (1975). Discrete multivariate analysis. Cambridge, MA: MIT Press.
Bjorck, A. (1967). Solving linear least squares problems by Gram-Schmidt orthonormalization. Bit, 7, 1-21.
Blackman, R. B., & Tukey, J. (1958). The measurement of power spectral from the point of view of communication engineering. New York: Dover.
Blackwelder, R. A. (1966). Taxonomy: A text and reference book. New York: Wiley.
Blalock, H. M. (1972). Social statistics (2nd ed.). New York:McGraw-Hill
Bliss, C. I. (1934). The method of probits. Science, 79, 38-39.
Bloomfield, P. (1976). Fourier analysis of time series: An introduction. New York: Wiley.
Bock, R. D. (1963). Programming univariate and multivariate analysis of variance. Technometrics, 5, 95-117.
Bock, R. D. (1975). Multivariate statistical methods in behavioral research. New York: McGraw-Hill.
Bolch, B.W., & Huang, C. J. (1974). Multivariate statistical methods for business and economics. Englewood Cliffs, NJ: Prentice-Hall.
Bollen, K. A. (1989). Structural equations with latent variables. New York: John Wiley & Sons.
Borg, I., & Lingoes, J. (1987). Multidimensional similarity structure analysis. New York: Springer.
Borg, I., & Shye, S. (in press). Facet Theory. Newbury Park: Sage.
Bowker, A. G. (1948). A test for symmetry in contingency tables. Journal of the American Statistical Association, 43, 572-574.
Bowley, A. L. (1897). Relations between the accuracy of an average and that of its constituent parts. Journal of the Royal Statistical Society, 60, 855-866.
Bowley, A. L. (1907). Elements of Statistics. London: P. S. King and Son.
Box, G. E. P. (1953). Non-normality and tests on variances. Biometrika, 40, 318-335.
Box, G. E. P. (1954a). Some theorems on quadratic forms applied in the study of analysis of variance problems: I.
Effect of inequality of variances in the one-way classification. Annals of Mathematical Statistics, 25, 290-302.
Box, G. E. P. (1954b). Some theorems on quadratic forms applied in the study of analysis of variance problems: II. Effect of inequality of variances and of correlation of errors in the two-way classification. Annals of Mathematical Statistics, 25, 484-498.
Box, G. E. P., & Anderson, S. L. (1955). Permutation theory in the derivation of robust criteria and the study of departures from assumptions. Journal of the Royal Statistical Society, 17, 1-34.
Box, G. E. P., & Behnken, D. W. (1960). Some new three level designs for the study of quantitative variables. Technometrics, 2, 455-475.
Box, G. E. P., & Cox, D. R. (1964). An analysis of transformations. Journal of the Royal Statistical Society, 26, 211-253.
Box, G. E. P., & Cox, D. R. (1964). An analysis of transformations. Journal of the Royal Statistical Society, B26, 211-234.
Box, G. E. P., & Draper, N. R. (1987). Empirical model-building and response surfaces. New York: Wiley.
Box, G. E. P., & Jenkins, G. M. (1970). Time series analysis. San Francisco: Holden Day.
Box, G. E. P., & Jenkins, G. M. (1976). Time series analysis: Forecasting and control. San Francisco: Holden-Day.
Box, G. E. P., & Tidwell, P. W. (1962). Transformation of the independent variables. Technometrics, 4, 531-550.
Box, G. E. P., & Wilson, K. B. (1951). On the experimental attainment of optimum conditions. Journal of the Royal Statistical Society, Ser. B, 13, 1-45.
Box, G. E. P., Hunter, W. G., & Hunter, S. J. (1978). Statistics for experimenters: An introduction to design, data analysis, and model building. New York: Wiley.
Breiman, L., Friedman, J. H., Olshen, R. A., & Stone, C. J. (1984). Classification and regression trees. Monterey, CA: Wadsworth & Brooks/Cole Advanced Books & Software.
Brenner, J. L., et al. (1968). Difference equations in forecasting formulas. Management Science, 14, 141-159.
Brent, R. F. (1973). Algorithms for minimization without derivatives. Englewood Cliffs, NJ: Prentice-Hall.
Breslow, N. E. (1970). A generalized Kruskal-Wallis test for comparing K samples subject to unequal pattern of censorship. Biometrika, 57, 579-594.
Breslow, N. E. (1974). Covariance analysis of censored survival data. Biometrics, 30, 89-99.
Brigham, E. O. (1974). The fast Fourier transform. Englewood Cliffs, NJ: Prentice-Hall.
Brillinger, D. R. (1975). Time series: Data analysis and theory. New York: Holt, Rinehart. & Winston.
Brown, D. T. (1959). A note on approximations to discrete probability distributions. Information and Control, 2, 386-392.
Brown, R. G. (1959). Statistical forecasting for inventory control. New York: McGraw-Hill.
Brown, M. B., & Forsythe, A. B. (1974). Robust tests for the equality of variances. Journal of the American Statistical Association, 69, 264-267.
Browne, M. W. (1968). A comparison of factor analytic techniques. Psychometrika, 33, 267-334.
Browne, M. W. (1974). Generalized least squares estimators in the analysis of covariance structures. South African Statistical Journal, 8, 1-24.
Browne, M. W. (1982). Covariance Structures. In D. M. Hawkins (Ed.) Topics in Applied Multivariate Analysis. Cambridge, MA: Cambridge University Press.
Browne, M. W. (1984). Asymptotically distribution free methods for the analysis of covariance structures. British Journal of Mathematical and Statistical Psychology, 37, 62-83.
Browne, M. W., & Cudeck, R. (1990). Single sample cross-validation indices for covariance structures. Multivariate Behavioral Research, 24, 445-455.
Browne, M. W., & Cudeck, R. (1992). Alternative ways of assessing model fit. In K. A. Bollen and J. S. Long (Eds.), Testing structural equation models. Beverly Hills, CA: Sage.
Browne, M. W., & DuToit, S. H. C. (1982). AUFIT (Version 1). A computer programme for the automated fitting of nonstandard models for means and covariances.
Research Finding WS-27. Pretoria, South Africa: Human Sciences Research Council.
Browne, M. W., & DuToit, S. H. C. (1987). Automated fitting of nonstandard models. Report WS-39. Pretoria, South Africa: Human Sciences Research Council.
Browne, M. W., & DuToit, S. H. C. (1992). Automated fitting of nonstandard models. Multivariate Behavioral Research, 27, 269-300.
Browne, M. W., & Mels, G. (1992). RAMONA User's Guide. The Ohio State University: Department of Psychology.
Browne, M. W., & Shapiro, A. (1989). Invariance of covariance structures under groups of transformations. Research Report 89/4. Pretoria, South Africa: University of South Africa Department of Statistics.
Browne, M. W., & Shapiro, A. (1991). Invariance of covariance structures under groups of transformations. Metrika, 38, 335-345.
Brownlee, K. A. (1960). Statistical Theory and Methodology in Science and Engineering. New York: John Wiley.
Buffa, E. S. (1972). Operations management: Problems and models (3rd. ed.). New York: Wiley.
Buja, A., & Tukey, P. A. (Eds.) (1991). Computing and Graphics in Statistics. New York: Springer-Verlag.
Buja, A., Fowlkes, E. B., Keramidas, E. M., Kettenring, J. R., Lee, J. C., Swayne, D. F., & Tukey, P. A. (1986). Discovering features of multivariate data through statistical graphics. Proceedings of the Section on Statistical Graphics, American Statistical Association, 98-103.
Burman, J. P. (1979). Seasonal adjustment - a survey. Forecasting, Studies in Management Science, 12, 45-57.
Burns, L. S., & Harman, A. J. (1966). The complex metropolis, Part V of profile of the Los Angeles metropolis: Its people and its homes. Los Angeles: University of Chicago Press.
Burt, C. (1950). The factorial analysis of qualitative data. British Journal of Psychology, 3, 166-185.
Campbell D. T., & Fiske, D. W. (1959). Convergent and discriminant validation by the multitrait-multimethod matrix. Psychological Bulletin, 56, 81-105
Carmines, E. G.
, & Zeller, R. A. (1980). Reliability and validity assessment. Beverly Hills, CA: Sage Publications.
Carrol, J. D., Green, P. E., and Schaffer, C. M. (1986). Interpoint distance comparisons in correspondence analysis. Journal of Marketing Research, 23, 271-280.
Carroll, J. D., & Wish, M. (1974). Multidimensional perceptual models and measurement methods. In E. C. Carterette and M. P. Friedman (Eds.), Handbook of perception. (Vol. 2, pp. 391-447). New York: Academic Press.
Cattell, R. B. (1966). The scree test for the number of factors. Multivariate Behavioral Research, 1, 245-276.
Cattell, R. B., & Jaspers, J. A. (1967). A general plasmode for factor analytic exercises and research. Multivariate Behavioral Research Monographs.
Chambers, J. M., Cleveland, W. S., Kleiner, B., & Tukey, P. A. (1983). Graphical methods for data analysis. Bellmont, CA: Wadsworth.
Chan, L. K., Cheng, S. W., & Spiring, F. (1988). A new measure of process capability: Cpm. Journal of Quality Technology, 20, 162-175.
Chen, J. (1992). Some results on 2(nk) fractional factorial designs and search for minimum aberration designs. Annals of Statistics, 20, 2124-2141.
Chen, J., Sun, D. X., & Wu, C. F. J. (1993). A catalog of two-level and three-level fractional factorial designs with small runs. International Statistical Review, 61, 131-145.
Chen, J., & Wu, C. F. J. (1991). Some results on s(nk) fractional factorial designs with minimum aberration or optimal moments. Annals of Statistics, 19, 1028-1041.
Chernoff, H. (1973). The use of faces to represent points in k-dimensional space graphically. Journal of American Statistical Association, 68, 361-368.
Christ, C. (1966). Econometric models and methods. New York: Wiley.
Clarke, G. M., & Cooke, D. (1978). A basic course in statistics. London: Edward Arnold.
Clements, J. A. (1989). Process capability calculations for non-normal distributions. Quality Progress. September, 95-100.
Cleveland, W. S.
(1979). Robust locally weighted regression and smoothing scatterplots. Journal of the American Statistical Association, 74, 829-836.
Cleveland, W. S. (1984). Graphs in scientific publications. The American Statistician, 38, 270-280.
Cleveland, W. S. (1985). The elements of graphing data. Monterey, CA: Wadsworth.
Cleveland, W. S. (1993). Visualizing data. Murray Hill, NJ: AT&T.
Cleveland, W. S., Harris, C. S., & McGill, R. (1982). Judgements of circle sizes on statistical maps. Journal of the American Statistical Association, 77, 541-547.
Cliff, N. (1983). Some cautions concerning the application of causal modeling methods. Multivariate Behavioral Research, 18, 115-126.
Cochran, W. G. (1950). The comparison of percentages in matched samples. Biometrika, 37, 256-266.
Cole, D. A., Maxwell, S. E., Arvey, R., & Salas, E. (1993). Multivariate group comparisons of variable systems: MANOVA and structural equation modeling. Psychological Bulletin, 114, 174-184.
Connor, W. S., & Young, S. (1984). Fractional factorial experiment designs for experiments with factors at two and three levels. In R. A. McLean & V. L. Anderson (Eds.), Applied factorial and fractional designs. New York: Marcel Dekker.
Connor, W. S., & Zelen, M. (1984). Fractional factorial experiment designs for factors at three levels. In R. A. McLean & V. L. Anderson (Eds.), Applied factorial and fractional designs. New York: Marcel Dekker.
Conover, W. J. (1974). Some reasons for not using the Yates continuity correction on 2 x 2 contingency tables. Journal of the American Statistical Association, 69, 374-376.
Conover, W. J., Johnson, M. E., & Johnson, M. M. (1981). A comparative study of tests for homogeneity of variances with applications to the outer continental shelf bidding data. Technometrics, 23, 357-361.
Cook, R. D. (1977). Detection of influential observations in linear regression. Technometrics, 19, 15-18.
Cook, R. D., & Nachtsheim, C. J.
(1980). A comparison of algorithms for constructing exact D-optimal designs. Technometrics, 22, 315-324.
Cook, R. D., & Weisberg, S. (1982). Residuals and Influence in Regression. (Monographs on statistics and applied probability). New York: Chapman and Hall.
Cooke, D., Craven, A. H., & Clarke, G. M. (1982). Basic statistical computing. London: Edward Arnold.
Cooley, J. W., & Tukey, J. W. (1965). An algorithm for the machine computation of complex Fourier series. Mathematics of Computation, 19, 297-301.
Cooley, W. W., & Lohnes, P. R. (1971). Multivariate data analysis. New York: Wiley.
Cooley, W. W., & Lohnes, P. R. (1976). Evaluation research in education. New York: Wiley.
Coombs, C. H. (1950). Psychological scaling without a unit of measurement. Psychological Review, 57, 145-158.
Coombs, C. H. (1964). A theory of data. New York: Wiley.
Corballis, M. C., & Traub, R. E. (1970). Longitudinal factor analysis. Psychometrika, 35, 79-98.
Corbeil, R. R., & Searle, S. R. (1976). Restricted maximum likelihood (REML) estimation of variance components in the mixed model. Technometrics, 18, 31-38.
Cormack, R. M. (1971). A review of classification. Journal of the Royal Statistical Society, 134, 321-367.
Cornell, J. A. (1990a). How to run mixture experiments for product quality. Milwaukee, Wisconsin: ASQC.
Cornell, J. A. (1990b). Experiments with mixtures: designs, models, and the analysis of mixture data (2nd ed.). New York: Wiley.
Cox, D. R. (1957). Note on grouping. Journal of the American Statistical Association, 52, 543-547.
Cox, D. R. (1959). The analysis of exponentially distributed life-times with two types of failures. Journal of the Royal Statistical Society, 21, 411-421.
Cox, D. R. (1964). Some applications of exponential ordered scores. Journal of the Royal Statistical Society, 26, 103-110.
Cox, D. R. (1970). The analysis of binary data. New York: Halsted Press.
Cox, D. R. (1972). Regression models and life tables. Journal of the Royal Statistical Society, 34, 187-220.
Cox, D. R., & Oakes, D. (1984). Analysis of survival data. New York: Chapman & Hall.
Cramer, H. (1946). Mathematical methods in statistics. Princeton, NJ: Princeton University Press.
Crowley, J., & Hu, M. (1977). Covariance analysis of heart transplant survival data. Journal of the American Statistical Association, 72, 27-36.
Cudeck, R. (1989). Analysis of correlation matrices using covariance structure models. Psychological Bulletin, 105, 317-327.
Cudeck, R., & Browne, M. W. (1983). Cross-validation of covariance structures. Multivariate Behavioral Research, 18, 147-167.
Cutler, S. J., & Ederer, F. (1958). Maximum utilization of the life table method in analyzing survival. Journal of Chronic Diseases, 8, 699-712.
Dahlquist, G., & Bjorck, A. (1974). Numerical Methods. Englewood Cliffs, NJ: Prentice-Hall.
Daniel, C. (1976). Applications of statistics to industrial experimentation. New York: Wiley.
Daniell, P. J. (1946). Discussion on symposium on autocorrelation in time series. Journal of the Royal Statistical Society, Suppl. 8, 88-90.
Daniels, H. E. (1939). The estimation of components of variance. Supplement to the Journal of the Royal Statistical Society, 6, 186-197.
Darlington, R. B. (1990). Regression and linear models. New York: McGraw-Hill.
Darlington, R. B., Weinberg, S., & Walberg, H. (1973). Canonical variate analysis and related techniques. Review of Educational Research, 43, 433-454.
DataMyte (1992). DataMyte handbook. Minnetonka, MN.
David, H. A. (1995). First (?) occurrence of common terms in mathematical statistics. The American Statistician, 49, 121-133.
Davies, P. M., & Coxon, A. P. M. (1982). Key texts in multidimensional scaling. Exeter, NH: Heinemann Educational Books.
Davis, C. S., & Stephens, M. A. Approximate percentage points using Pearson curves. Applied Statistics, 32, 322-327.
De Boor, C. (1978). A practical guide to splines. New York: Springer-Verlag.
De Gruitjer, P. N.
M., & Van Der Kamp, L. J. T. (Eds.). (1976). Advances in psychological and educational measurement. New York: Wiley.
Deming, S. N., & Morgan, S. L. (1993). Experimental design: A chemometric approach. (2nd ed.). Amsterdam, The Netherlands: Elsevier Science Publishers B.V.
Deming, W. E., & Stephan, F. F. (1940). The sampling procedure of the 1940 population census. Journal of the American Statistical Association, 35, 615-630.
Dempster, A. P. (1969). Elements of Continuous Multivariate Analysis. San Francisco: Addison-Wesley.
Dempster, A. P., Laird, N. M., & Rubin, D. B. (1977). Maximum likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical Society, 39, 1-38.
Dennis, J. E., & Schnabel, R. B. (1983). Numerical methods for unconstrained optimization and nonlinear equations. Englewood Cliffs, NJ: Prentice Hall.
Derringer, G., & Suich, R. (1980). Simultaneous optimization of several response variables. Journal of Quality Technology, 12, 214-219.
Diamond, W. J. (1981). Practical experimental design. Belmont, CA: Wadsworth.
Dijkstra, T. K. (1990). Some properties of estimated scale invariant covariance structures. Psychometrika, 55, 327-336.
Dinneen, L. C., & Blakesley, B. C. (1973). A generator for the sampling distribution of the Mann Whitney U statistic. Applied Statistics, 22, 269-273.
Dixon, W. J. (1954). Power under normality of several non-parametric tests. Annals of Mathematical Statistics, 25, 610-614.
Dixon, W. J., & Massey, F. J. (1983). Introduction to statistical analysis (4th ed.). New York: McGraw-Hill.
Dodd, B. (1979). Lip reading in infants: Attention to speech presented in- and out-of-synchrony. Cognitive Psychology, 11, 478-484.
Dodge, Y. (1985). Analysis of experiments with missing data. New York: Wiley.
Dodge, Y., Fedorov, V. V., & Wynn, H. P. (1988). Optimal design and analysis of experiments. New York: North-Holland.
Dodson, B. (1994). Weibull analysis.
Milwaukee, Wisconsin: ASQC.
Doyle, P. (1973). The use of Automatic Interaction Detection and similar search procedures. Operational Research Quarterly, 24, 465-467.
Duncan, A. J. (1974). Quality control and industrial statistics. Homewood, IL: Richard D. Irwin.
Duncan, O. D., Haller, A. O., & Portes, A. (1968). Peer influence on aspiration: a reinterpretation. American Journal of Sociology, 74, 119-137.
Durbin, J. (1970). Testing for serial correlation in least-squares regression when some of the regressors are lagged dependent variables. Econometrica, 38, 410-421.
Durbin, J., & Watson, G. S. (1951). Testing for serial correlations in least squares regression. II. Biometrika, 38, 159-178.
Dykstra, O. Jr. (1971). The augmentation of experimental data to maximize |X'X|. Technometrics, 13, 682-688.
Eason, E. D., & Fenton, R. G. (1974). A comparison of numerical optimization methods for engineering design. ASME Paper 73-DET-17.
Edgeworth, F. Y. (1885). Methods of statistics. In Jubilee Volume, Royal Statistical Society, 181-217.
Efron, B. (1982). The jackknife, the bootstrap, and other resampling plans. Philadelphia, Pa. Society for Industrial and Applied Mathematics.
Eisenhart, C. (1947). The assumptions underlying the analysis of variance. Biometrics, 3, 1-21.
Elandt-Johnson, R. C., & Johnson, N. L. (1980). Survival models and data analysis. New York: Wiley.
Elliott, D. F., & Rao, K. R. (1982). Fast transforms: Algorithms, analyses, applications. New York: Academic Press.
Elsner, J. B., Lehmiller, G. S., & Kimberlain, T. B. (1996). Objective classification of Atlantic hurricanes. Journal of Climate, 9, 2880-2889.
Enslein, K., Ralston, A., & Wilf, H. S. (1977). Statistical methods for digital computers. New York: Wiley.
Euler, L. (1782). Recherches sur une nouvelle espece de quarres magiques. Verhandelingen uitgegeven door het zeeuwsch Genootschap der Wetenschappen te Vlissingen, 9, 85-239. (Reproduced in Leonhardi Euleri Opera Omnia.
Sub auspiciis societatis scientiarium naturalium helveticae, 1st series, 7, 291-392.)
Evans, M., Hastings, N., & Peacock, B. (1993). Statistical Distributions. New York: Wiley.
Everitt, B. S. (1977). The analysis of contingency tables. London: Chapman & Hall.
Everitt, B. S. (1984). An introduction to latent variable models. London: Chapman and Hall.
Ewan, W. D. (1963). When and how to use Cu-sum charts. Technometrics, 5, 1-32.
Fayyad, U. M., Piatetsky-Shapiro, G., Smyth, P., & Uthurusamy, R. (Eds.). 1996. Advances in Knowledge Discovery and Data Mining. Cambridge, MA: The MIT Press.
Fayyad, U. S., & Uthurusamy, R. (Eds.) (1994). Knowledge Discovery in Databases; Papers from the 1994 AAAI Workshop. Menlo Park, CA: AAAI Press.
Feigl, P., & Zelen, M. (1965). Estimation of exponential survival probabilities with concomitant information. Biometrics, 21, 826-838.
Feller, W. (1948). On the Kolmogorov-Smirnov limit theorems for empirical distributions. Annals of Mathematical Statistics, 19, 177-189.
Fetter, R. B. (1967). The quality control system. Homewood, IL: Richard D. Irwin.
Fienberg, S. E. (1977). The analysis of cross-classified categorical data. Cambridge, MA: MIT Press.
Finn, J. D. (1974). A general model for multivariate analysis. New York: Holt, Rinehart & Winston.
Finn, J. D. (1977). Multivariate analysis of variance and covariance. In K. Enslein, A. Ralston, and H. S. Wilf (Eds.), Statistical methods for digital computers. Vol. III. (pp. 203-264). New York: Wiley.
Finney, D. J. (1944). The application of probit analysis to the results of mental tests. Psychometrika, 9, 31-39.
Finney, D. J. (1971). Probit analysis. Cambridge, MA: Cambridge University Press.
Fisher, R. A. (1918). The correlation between relatives on the supposition of Mendelian inheritance. Transactions of the Royal Society of Edinbrugh, 52, 399-433.
Fisher, R. A. (1922). On the mathematical foundations of theoretical statistics. Philosophical Transactions of the Royal Society of London, Ser.
A, 222, 309-368.
Fisher, R. A. (1922). On the interpretation of Chi- square from contingency tables, and the calculation of p. Journal of the Royal Statistical Society, 85, 87-94.
Fisher, R. A. (1926). The arrangement of field experiments. Journal of the Ministry of Agriculture of Great Britain, 33, 503-513.
Fisher, R. A. (1928). The general sampling distribution of the multiple correlation coefficient. Proceedings of the Royal Society of London, Ser. A, 121, 654-673.
Fisher, R. A. (1935). The Design of Experiments. Edinburgh: Oliver and Boyd.
Fisher, R. A. (1936). The use of multiple measurements in taxonomic problems. Annals of Eugenics, 7, 179-188.
Fisher, R. A. (1936). Statistical Methods for Research Workers (6th ed.). Edinburgh: Oliver and Boyd.
Fisher, R. A. (1938). The mathematics of experimentation. Nature, 142, 442-443.
Fisher, R. A., & Yates, F. (1934). The 6 x 6 Latin squares. Proceedings of the Cambridge Philosophical Society, 30, 492-507.
Fisher, R. A., & Yates, F. (1938). Statistical Tables for Biological, Agricultural and Medical Research. London: Oliver and Boyd.
Fletcher, R. (1969). Optimization. New York: Academic Press.
Fletcher, R., & Powell, M. J. D. (1963). A rapidly convergent descent method for minimization. Computer Journal, 6, 163-168.
Fletcher, R., & Reeves, C. M. (1964). Function minimization by conjugate gradients. Computer Journal, 7, 149-154.
Fomby, T.B., Hill, R.C., & Johnson, S.R. (1984). Advanced econometric methods. New York: Springer-Verlag.
Ford Motor Company, Ltd. & GEDAS (1991). Test examples for SPC software.
Franklin, M. F. (1984). Constructing tables of minimum aberration p(nm) designs. Technometrics, 26, 225-232.
Fraser, C., & McDonald, R. P. (1988). COSAN: Covariance structure analysis. Multivariate Behavioral Research, 23, 263-265.
Friedman, M. (1937). The use of ranks to avoid the assumption of normality implicit in the analysis of variance. Journal of the American Statistical Association, 32, 675-701.
Friedman, M. (1940). A comparison of alternative tests of significance for the problem of m rankings. Annals of Mathematical Statistics, 11, 86-92.
Fries, A., & Hunter, W. G. (1980). Minimum aberration 2 (kp) designs. Technometrics, 22, 601-608.
Frost, P. A. (1975). Some properties of the Almon lag technique when one searches for degree of polynomial and lag. Journal of the American Statistical Association, 70, 606-612.
Fuller, W. A. (1976). Introduction to statistical time series. New York: Wiley.
Gaddum, J. H. (1945). Lognormal distributions. Nature, 156, 463-466.
Gale, N., & Halperin, W. C. (1982). A case for better graphics: The unclassed choropleth map. The American Statistician, 36, 330-336.
Galil, Z., & Kiefer, J. (1980). Time- and space-saving computer methods, related to Mitchell's DETMAX, for finding D-optimum designs. Technometrics, 22, 301-313.
Galton, F. (1882). Report of the anthropometric committee. In Report of the 51st Meeting of the British Association for the Advancement of Science, 1881, 245-260.
Galton, F. (1885). Section H. Anthropology. Opening address by Francis Galton. Nature, 32, 507- 510.
Galton, F. (1885). Some results of the anthropometric laboratory. Journal of the Anthropological Institute, 14, 275-287.
Galton, F. (1888). Co-relations and their measurement. Proceedings of the Royal Society of London, 45, 135-145.
Galton, F. (1889). Natural Inheritance. London: Macmillan.
Ganguli, M. (1941). A note on nested sampling. Sankhya, 5, 449-452.
Gara, M. A., & Rosenberg, S. (1979). The identification of persons as supersets and subsets in free-response personality descriptions. Journal of Personality and Social Psychology, 37, 2161-2170.
Gara, M. A., & Rosenberg, S. (1981). Linguistic factors in implicit personality theory. Journal of Personality and Social Psychology, 41, 450-457.
Gardner, E. S., Jr. (1985). Exponential smoothing: The state of the art. Journal of Forecasting, 4, 1-28.
Garvin, D. A. (1987). Competing on the eight dimensions of quality. Harvard Business Review, November/December, 101-109.
Gbur, E., Lynch, M., & Weidman, L. (1986). An analysis of nine rating criteria on 329 U. S. metropolitan areas. Proceedings of the Section on Statistical Graphics, American Statistical Association, 104-109.
Gedye, R. (1968). A manager's guide to quality and reliability. New York: Wiley.
Gehan, E. A. (1965a). A generalized Wilcoxon test for comparing arbitrarily singly-censored samples. Biometrika, 52, 203-223.
Gehan, E. A. (1965b). A generalized two-sample Wilcoxon test for doubly-censored data. Biometrika, 52, 650-653.
Gehan, E. A., & Siddiqui, M. M. (1973). Simple regression methods for survival time studies. Journal of the American Statistical Association, 68, 848-856.
Gehan, E. A., & Thomas, D. G. (1969). The performance of some two sample tests in small samples with and without censoring. Biometrika, 56, 127-132.
Gerald, C. F., & Wheatley, P. O. (1989). Applied numerical analysis (4th ed.). Reading, MA: Addison Wesley.
Gibbons, J. D. (1976). Nonparametric methods for quantitative analysis. New York: Holt, Rinehart, & Winston.
Gibbons, J. D. (1985). Nonparametric statistical inference (2nd ed.). New York: Marcel Dekker.
Gifi, A. (1981). Nonlinear multivariate analysis. Department of Data Theory, The University of Leiden. The Netherlands.
Gifi, A. (1990). Nonlinear multivariate analysis. New York: Wiley.
Gill, P. E., & Murray, W. (1972). Quasi-Newton methods for unconstrained optimization. Journal of the Institute of Mathematics and its Applications, 9, 91-108.
Gill, P. E., & Murray, W. (1974). Numerical methods for constrained optimization. New York: Academic Press.
Gini, C. (1911). Considerazioni sulle probabilita a posteriori e applicazioni al rapporto dei sessi nelle nascite umane. Studi Economico-Giuridici della Universita de Cagliari, Anno III, 133-171.
Glass, G. V., & Stanley, J. (1970). Statistical methods in education and Psychology. Englewood Cliffs, NJ: Prentice-Hall.
Glass, G V., & Hopkins, K. D. (1996). Statistical methods in education and psychology. Needham Heights, MA: Allyn & Bacon.
Glasser, M. (1967). Exponential survival with covariance. Journal of the American Statistical Association, 62, 561-568.
Gnanadesikan, R., Roy, S., & Srivastava, J. (1971). Analysis and design of certain quantitative multiresponse experiments. Oxford: Pergamon Press, Ltd.
Golub, G. H., & Van Loan, C. F. (1983). Matrix computations. Baltimore: Johns Hopkins University Press.
Goodman, L .A., & Kruskal, W. H. (1972). Measures of association for cross-classifications IV: Simplification of asymptotic variances. Journal of the American Statistical Association, 67, 415-421.
Goodman, L. A. (1954). Kolmogorov-Smirnov tests for psychological research. Psychological Bulletin, 51, 160-168.
Goodman, L. A. (1971). The analysis of multidimensional contingency tables: Stepwise procedures and direct estimation methods for models building for multiple classification. Technometrics, 13, 33-61.
Goodman, L. A., & Kruskal, W. H. (1954). Measures of association for cross-classifications. Journal of the American Statistical Association, 49, 732-764.
Goodman, L. A., & Kruskal, W. H. (1959). Measures of association for cross-classifications II: Further discussion and references. Journal of the American Statistical Association, 54, 123-163.
Goodman, L. A., & Kruskal, W. H. (1963). Measures of association for cross-classifications III: Approximate sampling theory. Journal of the American Statistical Association, 58, 310-364.
Grant, E. L., & Leavenworth, R. S. (1980). Statistical quality control (5th ed.). New York: McGraw-Hill.
Green, P. E., & Carmone, F. J. (1970). Multidimensional scaling and related techniques in marketing analysis. Boston: Allyn & Bacon.
Greenacre, M. J. (1984). Theory and applications of correspondence analysis. New York: Academic Press.
Greenacre, M. J. (1988). Correspondence analysis of multivariate categorical data by weighted least-squares. Biometrica, 75, 457-467.
Greenacre, M. J. & Hastie, T. (1987). The geometric interpretation of correspondence analysis. Journal of the American Statistical Association, 82, 437-447.
Greenhouse, S. W., & Geisser, S. (1958). Extension of Box's results on the use of the F distribution in multivariate analysis. Annals of Mathematical Statistics, 29, 95-112.
Greenhouse, S. W., & Geisser, S. (1959). On methods in the analysis of profile data. Psychometrika, 24, 95-112.
Gross, A. J., & Clark, V. A. (1975). Survival distributions: Reliability applications in the medical sciences. New York: Wiley.
Gruska, G. F., Mirkhani, K., & Lamberson, L. R. (1989). Non-Normal data Analysis. Garden City, MI: Multiface Publishing.
Gruvaeus, G., & Wainer, H. (1972). Two additions to hierarchical cluster analysis. The British Journal of Mathematical and Statistical Psychology, 25, 200-206.
Guttman, L. (1954). A new approach to factor analysis: the radex. In P. F. Lazarsfeld (Ed.), Mathematical thinking in the social sciences. New York: Columbia University Press.
Guttman, L. (1968). A general nonmetric technique for finding the smallest coordinate space for a configuration of points. Pyrometrical, 33, 469-506.
Haberman, S. J. (1972). Loglinear fit for contingency tables. Applied Statistics, 21, 218-225.
Haberman, S. J. (1974). The analysis of frequency data. Chicago: University of Chicago Press.
Hahn, G. J., & Shapiro, S. S. (1967). Statistical models in engineering. New York: Wiley.
Hakstian, A. R., Rogers, W. D., & Cattell, R. B. (1982). The behavior of numbers of factors rules with simulated data. Multivariate Behavioral Research, 17, 193-219.
Hald, A. (1949). Maximum likelihood estimation of the parameters of a normal distribution which is truncated at a known point. Skandinavisk Aktuarietidskrift, 1949, 119-134.
Hald, A. (1952). Statistical theory with engineering applications. New York: Wiley.
Harman, H. H. (1967). Modern factor analysis. Chicago: University of Chicago Press.
Harris, R. J. (1976). The invalidity of partitioned U tests in canonical correlation and multivariate analysis of variance. Multivariate Behavioral Research, 11, 353-365.
Hart, K. M., & Hart, R. F. (1989). Quantitative methods for quality improvement. Milwaukee, WI: ASQC Quality Press.
Hartigan, J. A. (1975). Clustering algorithms. New York: Wiley.
Hartigan, J. A. & Wong, M. A. (1978). Algorithm 136. A k-means clustering algorithm. Applied Statistics, 28, 100.
Harrison, D. & Rubinfield, D. L. (1978). Hedonic prices and the demand for clean air. Journal of Environmental Economics and Management, 5, 81-102.
Hartley, H. O. (1959). Smallest composite designs for quadratic response surfaces. Biometrics, 15, 611-624.
Harville, D. A. (1977). Maximum likelihood approaches to variance component estimation and to related problems. Journal of the American Statistical Association, 72, 320-340.
Haskell, A. C. (1922). Graphic Charts in Business. New York: Codex.
Haviland, R. P. (1964). Engineering reliability and long life design. Princeton, NJ: Van Nostrand.
Hayduk, L. A. (1987). Structural equation modelling with LISREL: Essentials and advances. Baltimore: The Johns Hopkins University Press.
Haykin, S. (1994). Neural Networks: A Comprehensive Foundation. New York: Macmillan College Publishing.
Hays, W. L. (1981). Statistics (3rd ed.). New York: CBS College Publishing.
Hays, W. L. (1988). Statistics (4th ed.). New York: CBS College Publishing.
Heiberger, R. M. (1989). Computation for the analysis of designed experiments. New York: Wiley.
Hemmerle, W. J., & Hartley, H., O. (1973). Computing maximum likelihood estimates for the mixed A.O.V. model using the W transformation. Technometrics, 15, 819-831.
Henley, E. J., & Kumamoto, H. (1980). Reliability engineering and risk assessment. New York: Prentice-Hall.
Hettmansperger, T. P. (1984). Statistical inference based on ranks. New York: Wiley.
Hibbs, D. (1974). Problems of statistical estimation and causal inference in dynamic time series models.
In H. Costner (Ed.), Sociological Methodology 1973/1974 (pp. 252-308). San Francisco: Jossey-Bass.
Hill, I. D., Hill, R., & Holder, R. L. (1976). Fitting Johnson curves by moments. Applied Statistics. 25, 190-192.
Hilton, T. L. (1969). Growth study annotated bibliography. Princeton, NJ: Educational Testing Service Progress Report 69-11.
Hochberg, J., & Krantz, D. H. (1986). Perceptual properties of statistical graphs. Proceedings of the Section on Statistical Graphics, American Statistical Association, 29-35.
Hocking, R. R., & Speed, F. M. (1975). A full rank analysis of some linear model problems. Journal of the American Statistical Association, 70, 707-712.
Hocking, R. R. (1985). The analysis of linear models. Monterey, CA: Brooks/Cole.
Hocking, R. R. (1996). Methods and Applications of Linear Models. Regression and the Analysis of Variance. New York: Wiley.
Hoerl, A. E. (1962). Application of ridge analysis to regression problems. Chemical Engineering Progress, 58, 54-59.
Hoerl, A. E., & Kennard, R. W. (1970). Ridge regression: Applications to nonorthogonal problems. Technometrics, 12, 69-82.
Hoff, J. C. (1983). A practical guide to Box-Jenkins forecasting. London: Lifetime Learning Publications.
Hoffman, D. L. & Franke, G. R. (1986). Correspondence analysis: Graphical representation of categorical data in marketing research. Journal of Marketing Research, 13, 213-227.
Hogg, R. V., & Craig, A. T. (1970). Introduction to mathematical statistics. New York: Macmillan.
Holzinger, K. J., & Swineford, F. (1939). A study in factor analysis: The stability of a bi-factor solution. University of Chicago: Supplementary Educational Monographs, No. 48.
Hooke, R., & Jeeves, T. A. (1961). Direct search solution of numerical and statistical problems. Journal of the Association for Computing Machinery, 8, 212-229.
Hotelling, H. (1947). Multivariate quality control. In Eisenhart, Hastay, and Wallis (Eds.), Techniques of Statistical Analysis.
New York: McGraw-Hill.
Hotelling, H., & Pabst, M. R. (1936). Rank correlation and tests of significance involving no assumption of normality. Annals of Mathematical Statistics, 7, 29-43.
Hoyer, W., & Ellis, W. C. (1996). A graphical exploration of SPC. Quality Progress, 29, 65-73.
Hsu, P. L. (1938). Contributions to the theory of Student's t test as applied to the problem of two samples. Statistical Research Memoirs, 2, 1-24.
Huba, G. J., & Harlow, L. L. (1987). Robust structural equation models: implications for developmental psychology. Child Development, 58, 147-166.
Huberty, C. J. (1975). Discriminant analysis. Review of Educational Research, 45, 543-598.
Huynh, H., & Feldt, L. S. (1970). Conditions under which mean square ratios in repeated measures designs have exact F-distributions. Journal of the American Statistical Association, 65, 1582-1589.
Ireland, C. T., & Kullback, S. (1968). Contingency tables with given marginals. Biometrika, 55, 179-188.
Jaccard, J., Weber, J., & Lundmark, J. (1975). A multitrait-multimethod factor analysis of four attitude assessment procedures. Journal of Experimental Social Psychology, 11, 149-154.
Jacobs, D. A. H. (Ed.). (1977). The state of the art in numerical analysis. London: Academic Press.
Jacoby, S. L. S., Kowalik, J. S., & Pizzo, J. T. (1972). Iterative methods for nonlinear optimization problems. Englewood Cliffs, NJ: Prentice-Hall.
James, L. R., Mulaik, S. A., & Brett, J. M. (1982). Causal analysis. Assumptions, models, and data. Beverly Hills, CA: Sage Publications.
Jardine, N., & Sibson, R. (1971). Mathematical taxonomy. New York: Wiley.
Jastrow, J. (1892). On the judgment of angles and position of lines. American Journal of Psychology, 5, 214-248.
Jenkins, G. M., & Watts, D. G. (1968). Spectral analysis and its applications. San Francisco: Holden-Day.
Jennrich, R. I. (1970). An asymptotic test for the equality of two correlation matrices. Journal of the American Statistical Association, 65, 904-912.
Jennrich, R. I. (1977). Stepwise regression. In K. Enslein, A. Ralston, & H.S. Wilf (Eds.), Statistical methods for digital computers. New York: Wiley.
Jennrich. R. I. (1977). Stepwise discriminant analysis. In K. Enslein, A. Ralston, & H.S. Wilf (Eds.), Statistical methods for digital computers. New York: Wiley.
Jennrich, R. I., & Moore, R. H. (1975). Maximum likelihood estimation by means of nonlinear least squares. Proceedings of the Statistical Computing Section, American Statistical Association, 57-65.
Jennrich, R. I., & Sampson, P. F. (1968). Application of stepwise regression to non-linear estimation. Technometrics, 10, 63-72.
Jennrich, R. I., & Sampson, P. F. (1976). Newton-Raphson and related algorithms for maximum likelihood variance component estimation. Technometrics, 18, 11-17.
Jennrich, R. I., & Schuchter, M. D. (1986). Unbalanced repeated-measures models with structured covariance matrices. Biometrics, 42, 805-820.
Johnson, L. W., & Ries, R. D. (1982). Numerical Analysis (2nd ed.). Reading, MA: Addison Wesley.
Johnson, N. L. (1961). A simple theoretical approach to cumulative sum control charts. Journal of the American Statistical Association, 56, 83-92.
Johnson, N. L. (1965). Tables to facilitate fitting SU frequency curves. Biometrika, 52, 547.
Johnson, N. L., & Kotz, S. (1970). Continuous univariate distributions, Vol I and II. New York: Wiley.
Johnson, N. L., & Leone, F. C. (1962). Cumulative sum control charts - mathematical principles applied to their construction and use. Industrial Quality Control, 18, 15-21.
Johnson, N. L., Nixon, E., & Amos, D. E. (1963). Table of percentage points of pearson curves. Biometrika, 50, 459.
Johnson, N. L., Nixon, E., Amos, D. E., & Pearson, E. S. (1963). Table of percentage points of Pearson curves for given 1 and 2, expressed in standard measure. Biometrika, 50, 459-498.
Johnson, P. (1987). SPC for short runs: A programmed instruction workbook. Southfield, MI: Perry Johnson.
Johnson, S. C. (1967). Hierarchical clustering schemes. Psychometrika, 32, 241-254.
Johnston, J. (1972). Econometric methods. New York: McGraw-Hill.
Joreskog, K. G. (1973). A general model for estimating a linear structural equation system. In A. S. Goldberger and O. D. Duncan (Eds.), Structural Equation Models in the Social Sciences. New York: Seminar Press.
Joreskog, K. G. (1974). Analyzing psychological data by structural analysis of covariance matrices. In D. H. Krantz, R. C. Atkinson, R. D. Luce, and P. Suppes (Eds.), Contemporary Developments in Mathematical Psychology, Vol. II. New York: W. H. Freeman and Company.
Joreskog, K. G. (1978). Structural analysis of covariance and correlation matrices. Psychometrika, 43, 443-477.
Joreskog, K. G., & Lawley, D. N. (1968). New methods in maximum likelihood factor analysis. British Journal of Mathematical and Statistical Psychology, 21, 85-96.
Joreskog, K. G., & Sorbom, D. (1979). Advances in factor analysis and structural equation models. Cambridge, MA: Abt Books.
Joreskog, K. G., & Sorbom, D. (1982). Recent developments in structural equation modeling. Journal of Marketing Research, 19, 404-416.
Joreskog, K. G., & Sorbom, D. (1984). Lisrel VI. Analysis of linear structural relationships by maximum likelihood, instrumental variables, and least squares methods. Mooresville, Indiana: Scientific Software.
Joreskog, K. G., & Sorbom, D. (1989). Lisrel 7. A guide to the program and applications. Chicago, Illinois: SPSS Inc.
Judge, G. G., Griffith, W. E., Hill, R. C., Luetkepohl, H., & Lee, T. S. (1985). The theory and practice of econometrics. New York: Wiley.
Juran, J. M. (1960). Pareto, Lorenz, Cournot, Bernnouli, Juran and others. Industrial Quality Control, 17, 25.
Juran, J. M. (1962). Quality control handbook. New York: McGraw-Hill.
Juran, J. M., & Gryna, F. M. (1970). Quality planning and analysis. New York: McGraw-Hill.
Juran, J. M., & Gryna, F. M. (1980). Quality planning and analysis (2nd ed.).
New York: McGraw-Hill.
Juran, J. M., & Gryna, F. M. (1988). Juran's quality control handbook (4th ed.). New York: McGraw-Hill.
Kachigan, S. K. (1986). Statistical analysis: An interdisciplinary introduction to univariate & multivariate methods. New York: Redius Press.
Kackar, R. M. (1985). Off-line quality control, parameter design, and the Taguchi method. Journal of Quality Technology, 17, 176-188.
Kackar, R. M. (1986). Taguchi's quality philosophy: Analysis and commentary. Quality Progress, 19, 21-29.
Kahneman, D., Slovic, P., & Tversky, A. (1982). Judgment under uncertainty: Heuristics and biases. New York: Cambridge University Press.
Kaiser, H. F. (1958). The varimax criterion for analytic rotation in factor analysis. Pyrometrical, 23, 187-200.
Kaiser, H. F. (1960). The application of electronic computers to factor analysis. Educational and Psychological Measurement, 20, 141-151.
Kalbfleisch, J. D., & Prentice, R. L. (1980). The statistical analysis of failure time data. New York: Wiley.
Kane, V. E. (1986). Process capability indices. Journal of Quality Technology, 18, 41-52.
Kaplan, E. L., & Meier, P. (1958). Nonparametric estimation from incomplete observations. Journal of the American Statistical Association, 53, 457-481.
Karsten, K. G., (1925). Charts and graphs. New York: Prentice-Hall.
Kass, G. V. (1980). An exploratory technique for investigating large quantities of categorical data. Applied Statistics, 29, 119-127.
Keats, J. B., & Lawrence, F. P. (1997). Weibull maximum likelihood parameter estimates with censored data. Journal of Quality Technology, 29, 105-110.
Keeves, J. P. (1972). Educational environment and student achievement. Melbourne: Australian Council for Educational Research.
Kendall, M. G. (1940). Note on the distribution of quantiles for large samples. Supplement of the Journal of the Royal Statistical Society, 7, 83-85.
Kendall, M. G. (1948). Rank correlation methods. (1st ed.).
London: Griffin.
Kendall, M. G. (1975). Rank correlation methods (4th ed.). London: Griffin.
Kendall, M. G. (1984). Time Series. New York: Oxford University Press.
Kendall, M., & Ord, J. K. (1990). Time series (3rd ed.). London: Griffin.
Kendall, M., & Stuart, A. (1979). The advanced theory of statistics (Vol. 2). New York: Hafner.
Kennedy, A. D., & Gehan, E. A. (1971). Computerized simple regression methods for survival time studies. Computer Programs in Biomedicine, 1, 235-244.
Kennedy, W. J., & Gentle, J. E. (1980). Statistical computing. New York: Marcel Dekker, Inc.
Kenny, D. A. (1979). Correlation and causality. New York: Wiley.
Keppel, G. (1973). Design and analysis: A researcher's handbook. Engelwood Cliffs, NJ: Prentice-Hall.
Keppel, G. (1982). Design and analysis: A researcher's handbook (2nd ed.). Engelwood Cliffs, NJ: Prentice-Hall.
Keselman, H. J., Rogan, J. C., Mendoza, J. L., & Breen, L. L. (1980). Testing the validity conditions for repeated measures F tests. Psychological Bulletin, 87, 479-481.
Khuri, A. I., & Cornell, J. A. (1987). Response surfaces: Designs and analyses. New York: Marcel Dekker, Inc.
Kiefer, J., & Wolfowitz, J. (1960). The equivalence of two extremum problems. Canadian Journal of Mathematics, 12, 363-366.
Kim, J. O., & Mueller, C. W. (1978a). Factor analysis: Statistical methods and practical issues. Beverly Hills, CA: Sage Publications.
Kim, J. O., & Mueller, C. W. (1978b). Introduction to factor analysis: What it is and how to do it. Beverly Hills, CA: Sage Publications.
Kirk, D. B. (1973). On the numerical approximation of the bivariate normal (tetrachoric) correlation coefficient. Psychometrika, 38, 259-268.
Kirk, R. E. (1968). Experimental design: Procedures for the behavioral sciences. (1st ed.). Monterey, CA: Brooks/Cole.
Kirk, R. E. (1982). Experimental design: Procedures for the behavioral sciences. (2nd ed.). Monterey, CA: Brooks/Cole.
Kivenson, G. (1971). Durability and reliability in engineering design.
New York: Hayden.
Klecka, W. R. (1980). Discriminant analysis. Beverly Hills, CA: Sage.
Klein, L. R. (1974). A textbook of econometrics. Englewood Cliffs, NJ: Prentice-Hall.
Kline, P. (1979). Psychometrics and psychology. London: Academic Press.
Kline, P. (1986). A handbook of test construction. New York: Methuen.
Kmenta, J. (1971). Elements of econometrics. New York: Macmillan.
Knuth, Donald E. (1981). Seminumerical algorithms. 2nd ed., Vol 2 of: The art of computer programming. Reading, Mass.: Addison-Wesley.
Kolata, G. (1984). The proper display of data. Science, 226, 156-157.
Kolmogorov, A. (1941). Confidence limits for an unknown distribution function. Annals of Mathematical Statistics, 12, 461-463.
Korin, B. P. (1969). On testing the equality of k covariance matrices. Biometrika, 56, 216-218.
Kruskal, J. B. (1964). Nonmetric multidimensional scaling: A numerical method. Pyrometrical, 29, 1-27, 115-129.
Kruskal, J. B., & Wish, M. (1978). Multidimensional scaling. Beverly Hills, CA: Sage Publications.
Kruskal, W. H. (1952). A nonparametric test for the several sample problem. Annals of Mathematical Statistics, 23, 525-540.
Kruskal, W. H. (1975). Visions of maps and graphs. In J. Kavaliunas (Ed.), Auto-carto II, proceedings of the international symposium on computer assisted cartography. Washington, DC: U. S. Bureau of the Census and American Congress on Survey and Mapping.
Kruskal, W. H., & Wallis, W. A. (1952). Use of ranks in one-criterion variance analysis. Journal of the American Statistical Association, 47, 583-621.
Ku, H. H., & Kullback, S. (1968). Interaction in multidimensional contingency tables: An information theoretic approach. J. Res. Nat. Bur. Standards Sect. B, 72, 159-199.
Ku, H. H., Varner, R. N., & Kullback, S. (1971). Analysis of multidimensional contingency tables. Journal of the American Statistical Association, 66, 55-64.
Kullback, S. (1959). Information theory and statistics. New York: Wiley.
Kvalseth, T. O. (1985). Cautionary note about R2. The American Statistician, 39, 279-285.
Lagakos, S. W., & Kuhns, M. H. (1978). Maximum likelihood estimation for censored exponential survival data with covariates. Applied Statistics, 27, 190-197.
Lance, G. N., & Williams, W. T. (1966). A general theory of classificatory sorting strategies. Computer Journal, 9, 373.
Lance, G. N., & Williams, W. T. (1966). Computer programs for hierarchical polythetic classification ("symmetry analysis"). Computer Journal, 9, 60.
Larsen, W. A., & McCleary, S. J. (1972). The use of partial residual plots in regression analysis. Technometrics, 14, 781-790.
Lawless, J. F. (1982). Statistical models and methods for lifetime data. New York: Wiley.
Lawley, D. N., & Maxwell, A. E. (1971). Factor analysis as a statistical method. New York: American Elsevier.
Lawley, D. N., & Maxwell, A. E. (1971). Factor analysis as a statistical method (2nd. ed.). London: Butterworth & Company.
Lebart, L., Morineau, A., and Tabard, N. (1977). Techniques de la description statistique. Paris: Dunod.
Lebart, L., Morineau, A., and Warwick, K., M. (1984). Multivariate descriptive statistical analysis: Correspondence analysis and related techniques for large matrices. New York: Wiley.
Lee, E. T. (1980). Statistical methods for survival data analysis. Belmont, CA: Lifetime Learning.
Lee, E. T., & Desu, M. M. (1972). A computer program for comparing K samples with right-censored data. Computer Programs in Biomedicine, 2, 315-321.
Lee, E. T., Desu, M. M., & Gehan, E. A. (1975). A Monte-Carlo study of the power of some two-sample tests. Biometrika, 62, 425-532.
Lee, S., & Hershberger, S. (1990). A simple rule for generating equivalent models in covariance structure modeling. Multivariate Behavioral Research, 25, 313-334.
Legendre, A. M. (1805). Nouvelles Methodes pour la Determination des Orbites des Cometes. Paris: F. Didot.
Lehmann, E. L.
(1975). Nonparametrics: Statistical methods based on ranks. San Francisco: Holden-Day.
Lewicki, P., Hill, T., & Czyzewska, M. (1992). Nonconscious acquisition of information. American Psychologist, 47, 796-801.
Lieblein, J. (1953). On the exact evaluation of the variances and covariances of order statistics in samples form the extreme-value distribution. Annals of Mathematical Statistics, 24, 282-287.
Lieblein, J. (1955). On moments of order statistics from the Weibull distribution. Annals of Mathematical Statistics, 26, 330-333.
Lilliefors, H. W. (1967). On the Kolmogorov-Smirnov test for normality with mean and variance unknown. Journal of the American Statistical Association, 64, 399-402.
Lim, T.-S., Loh, W.-Y., & Shih, Y.-S. (1997). An emprical comparison of decision trees and other classification methods. Technical Report 979, Department of Statistics, University of Winconsin, Madison.
Lindeman, R. H., Merenda, P. F., & Gold, R. (1980). Introduction to bivariate and multivariate analysis. New York: Scott, Foresman, & Co.
Lindman, H. R. (1974). Analysis of variance in complex experimental designs. San Francisco: W. H. Freeman & Co.
Linfoot, E. H. (1957). An informational measure of correlation. Information and Control, 1, 50-55.
Linn, R. L. (1968). A Monte Carlo approach to the number of factors problem. Psychometrika, 33, 37-71.
Lipson, C., & Sheth, N. C. (1973). Statistical design and analysis of engineering experiments. New York: McGraw-Hill.
Lloyd, D. K., & Lipow, M. (1977). Reliability: Management, methods, and mathematics. New York: McGraw-Hill.
Loehlin, J. C. (1987). Latent variable models: An introduction to latent, path, and structural analysis. Hillsdale, NJ: Erlbaum.
Loh, W.-Y, & Shih, Y.-S. (1997). Split selection methods for classification trees. Statistica Sinica, 7, 815-840.
Loh, W.-Y., & Vanichestakul, N. (1988). Tree-structured classification via generalized discriminant analysis (with discussion). Journal of the American Statistical Association, 83, 715-728.
Long, J. S. (1983a). Confirmatory factor analysis. Beverly Hills: Sage.
Long, J. S. (1983b). Covariance structure models: An introduction to LISREL. Beverly Hills: Sage.
Longley, J. W. (1967). An appraisal of least squares programs for the electronic computer from the point of view of the user. Journal of the American Statistical Association, 62, 819-831.
Longley, J. W. (1984). Least squares computations using orthogonalization methods. New York: Marcel Dekker.
Lord, F. M. (1957). A significance test for the hypothesis that two variables measure the same trait except for errors of measurement. Psychometrika, 22, 207-220.
Lorenz, M. O. (1904). Methods of measuring the concentration of wealth. American Statistical Association Publication, 9, 209-219.
Lucas, J. M. (1976). The design and use of cumulative sum quality control schemes. Journal of Quality Technology, 8, 45-70.
Lucas, J. M. (1982). Combined Shewhart-CUSUM quality control schemes. Journal of Quality Technology, 14, 89-93.
Maddala, G. S. (1977) Econometrics. New York: McGraw-Hill.
Maiti, S. S., & Mukherjee, B. N. (1990). A note on the distributional properties of the Joreskog-Sorbom fit indices. Psychometrika, 55, 721-726.
Makridakis, S. G. (1983). Empirical evidence versus personal experience. Journal of Forecasting, 2, 295-306.
Makridakis, S. G. (1990). Forecasting, planning, and strategy for the 21st century. London: Free Press.
Makridakis, S. G., & Wheelwright, S. C. (1978). Interactive forecasting: Univariate and multivariate methods (2nd ed.). San Francisco, CA: Holden-Day.
Makridakis, S. G., & Wheelwright, S. C. (1989). Forecasting methods for management (5th ed.). New York: Wiley.
Makridakis, S. G., Wheelwright, S. C., & McGee, V. E. (1983). Forecasting: Methods and applications (2nd ed.). New York: Wiley.
Makridakis, S., Andersen, A., Carbone, R., Fildes, R., Hibon, M., Lewandowski, R., Newton, J., Parzen, R., & Winkler, R. (1982). The accuracy of extrapolation (time series) methods: Results of a forecasting competition. Journal of Forecasting, 1, 11-153.
Malinvaud, E. (1970). Statistical methods of econometrics. Amsterdam: North-Holland Publishing Co.
Mandel, B. J. (1969). The regression control chart. Journal of Quality Technology, 1, 3-10.
Mann, H. B., & Whitney, D. R. (1947). On a test of whether one of two random variables is stochastically larger than the other. Annals of Mathematical Statistics, 18, 50-60.
Mann, N. R., Schafer, R. E., & Singpurwalla, N. D. (1974). Methods for statistical analysis of reliability and life data. New York: Wiley.
Mann, N. R., Scheuer, R. M, & Fertig, K. W. (1973). A new goodness of fit test for the two-parameter Weibull or exteme value distribution. Communications in Statistics, 2, 383-400.
Mantel, N. (1966). Evaluation of survival data and two new rank order statistics arising in its consideration. Cancer Chemotherapy Reports, 50, 163-170.
Mantel, N. (1967). Ranking procedures for arbitrarily restricted observations. Biometrics, 23, 65-78.
Mantel, N. (1974). Comment and suggestion on the Yates continuity correction. Journal of the American Statistical Association, 69, 378-380.
Mantel, N., & Haenszel, W. (1959). Statistical aspects of the analysis of data from retrospective studies of disease. Journal of the National Cancer Institute, 22, 719-748.
Marascuilo, L. A., & McSweeney, M. (1977). Nonparametric and distribution free methods for the social sciences. Monterey, CA: Brooks/Cole.
Marple, S. L., Jr. (1987). Digital spectral analysis. Englewood Cliffs, NJ: Prentice-Hall.
Marsaglia, G. (1962). Random variables and computers. In J. Kozenik (Ed.), Information theory, statistical decision functions, random processes: Transactions of the third Prague Conference. Prague: Czechoslovak Academy of Sciences.
Mason, R. L., Gunst, R. F., & Hess, J. L. (1989). Statistical design and analysis of experiments with applications to engineering and science. New York: Wiley.
Massey, F. J., Jr. (1951). The Kolmogorov-Smirnov test for goodness of fit. Journal of the American Statistical Association, 46, 68-78.
Masters (1995). Neural, Novel, and Hybrid Algorithms for Time Series Predictions. New York: Wiley.
Matsueda, R. L., & Bielby, W. T. (1986). Statistical power in covariance structure models. In N. B. Tuma (Ed.), Sociological methodology. Washington, DC: American Sociological Association.
McArdle, J. J. (1978). A structural view of structural models. Paper presented at the Winter Workshop on Latent Structure Models Applied to Developmental Data, University of Denver, December, 1978.
McArdle, J. J., & McDonald, R. P. (1984). Some algebraic properties of the Reticular Action Model for moment structures. British Journal of Mathematical and Statistical Psychology, 37, 234-251.
McCleary, R., & Hay, R. A. (1980). Applied time series analysis for the social sciences. Beverly Hills, CA: Sage Publications.
McDonald, R. P. (1980). A simple comprehensive model for the analysis of covariance structures. British Journal of Mathematical and Statistical Psychology, 31, 59-72.
McDonald, R. P. (1989). An index of goodness-of-fit based on noncentrality. Journal of Classification, 6, 97-103.
McDonald, R. P., & Hartmann, W. M. (1992). A procedure for obtaining initial value estimates in the RAM model. Multivariate Behavioral Research, 27, 57-76.
McDonald, R. P., & Mulaik, S. A. (1979). Determinacy of common factors: A nontechnical review. Psychological Bulletin, 86, 297-306.
McDowall, D., McCleary, R., Meidinger, E. E., & Hay, R. A. (1980). Interrupted time series analysis. Beverly Hills, CA: Sage Publications.
McLachlan, G. J. (1992). Discriminant analysis and statistical pattern recognition. New York: Wiley.
McKenzie, E. (1984). General exponential smoothing and the equivalent ARMA process. Journal of Forecasting, 3, 333-344.
McKenzie, E. (1985). Comments on 'Exponential smoothing: The state of the art' by E. S. Gardner, Jr. Journal of Forecasting, 4, 32-36.
McLain, D. H. (1974). Drawing contours from arbitrary data points. The Computer Journal, 17, 318-324.
McLean, R. A., & Anderson, V. L. (1984). Applied factorial and fractional designs. New York: Marcel Dekker.
McLeod, A. I., & Sales, P. R. H. (1983). An algorithm for approximate likelihood calculation of ARMA and seasonal ARMA models. Applied Statistics, 211-223 (Algorithm AS).
McNemar, Q. (1947). Note on the sampling error of the difference between correlated proportions or percentages. Psychometrika, 12, 153-157.
McNemar, Q. (1969). Psychological statistics (4th ed.). New York: Wiley.
Melard, G. (1984). A fast algorithm for the exact likelihood of autoregressive-moving average models. Applied Statistics, 33, 104-119.
Mels, G. (1989). A general system for path analysis with latent variables. M. S. Thesis: Department of Statistics, University of South Africa.
Mendoza, J. L., Markos, V. H., & Gonter, R. (1978). A new perspective on sequential testing procedures in canonical analysis: A Monte Carlo evaluation. Multivariate Behavioral Research, 13, 371-382.
Meredith, W. (1964). Canonical correlation with fallible data. Psychometrika, 29, 55-65.
Miller, R. (1981). Survival analysis. New York: Wiley.
Milligan, G. W. (1980). An examination of the effect of six types of error perturbation on fifteen clustering algorithms. Psychometrika, 45, 325-342.
Milliken, G. A., & Johnson, D. E. (1984). Analysis of messy data: Vol. I. Designed experiments. New York: Van Nostrand Reinhold, Co.
Milliken, G. A., & Johnson, D. E. (1992). Analysis of messy data: Vol. I. Designed experiments. New York: Chapman & Hall.
Mitchell, T. J. (1974a). Computer construction of "D-optimal" first-order designs. Technometrics, 16, 211-220.
Mitchell, T. J. (1974b). An algorithm for the construction of "D-optimal" experimental designs. Technometrics, 16, 203-210.
Mittag, H. J. (1993). Qualitatsregelkarten. Munchen/Wien: Hanser Verlag.
Mittag, H. J., & Rinne, H. (1993). Statistical methods of quality assurance. London/New York: Chapman & Hall.
Monro, D. M. (1975). Complex discrete fast Fourier transform. Applied Statistics, 24, 153-160.
Monro, D. M., & Branch, J. L. (1976). The chirp discrete Fourier transform of general length. Applied Statistics, 26, 351-361.
Montgomery, D. C. (1976). Design and analysis of experiments. New York: Wiley.
Montgomery, D. C. (1985). Statistical quality control. New York: Wiley.
Montgomery, D. C. (1991) Design and analysis of experiments (3rd ed.). New York: Wiley.
Montgomery, D. C., & Wadsworth, H. M. (1972). Some techniques for multivariate quality control applications. Technical Conference Transactions. Washington, DC: American Society for Quality Control.
Montgomery, D. C., Johnson, L. A., & Gardiner, J. S. (1990). Forecasting and time series analysis (2nd ed.). New York: McGraw-Hill.
Mood, A. M. (1954). Introduction to the theory of statistics. New York: McGraw Hill.
Morgan, J. N., & Messenger, R. C. (1973). THAID: A sequential analysis program for the analysis of nominal scale dependent variables. Technical report, Institute of Social Research, University of Michigan, Ann Arbor.
Morgan, J. N., & Sonquist, J. A. (1973). Problems in the analysis of survey data, and a proposal. Journal of the American Statistical Association, 58, 415-434.
Morris, M., & Thisted, R. A. (1986). Sources of error in graphical perception: A critique and an experiment. Proceedings of the Section on Statistical Graphics, American Statistical Association, 43-48.
Morrison, A. S., Black, M. M., Lowe, C. R., MacMahon, B., & Yuasa, S. (1973). Some international differences in histology and survival in breast cancer. International Journal of Cancer, 11, 261-267.
Morrison, D. (1967). Multivariate statistical methods. New York: McGraw-Hill.
Moses, L. E. (1952). Non-parametric statistics for psychological research. Psychological Bulletin, 49, 122-143.
Mulaik, S. A. (1972). The foundations of factor analysis. New York: McGraw Hill.
Muth, J. F. (1960).
Optimal properties of exponentially weighted forecasts. Journal of the American Statistical Association, 55, 299-306.
Nachtsheim, C. J. (1979). Contributions to optimal experimental design. Ph.D. thesis, Department of Applied Statistics, University of Minnesota.
Nachtsheim, C. J. (1987). Tools for computer-aided design of experiments. Journal of Quality Technology, 19, 132-160.
Nelder, J. A., & Mead, R. (1965). A Simplex method for function minimization. Computer Journal, 7, 308-313.
Nelson, L. (1984). The Shewhart control chart - tests for special causes. Journal of Quality Technology, 15, 237-239.
Nelson, L. (1985). Interpreting Shewhart X-bar control charts. Journal of Quality Technology, 17, 114-116.
Nelson, W. (1982). Applied life data analysis. New York: Wiley.
Nelson, W. (1990). Accelerated testing: Statistical models, test plans, and data analysis. New York: Wiley.
Neter, J., Wasserman, W., & Kutner, M. H. (1985). Applied linear statistical models: Regression, analysis of variance, and experimental designs. Homewood, IL: Irwin.
Neter, J., Wasserman, W., & Kutner, M. H. (1989). Applied linear regression models (2nd ed.). Homewood, IL: Irwin.
Neyman, J., & Pearson, E. S. (1931). On the problem of k samples. Bulletin de l'Academie Polonaise des Sciences et Lettres, Ser. A, 460-481.
Neyman, J., & Pearson, E. S. (1933). On the problem of the most efficient tests of statistical hypothesis. Philosophical Transactions of the Royal Society of London, Ser. A, 231, 289-337.
Nisbett, R. E., Fong, G. F., Lehman, D. R., & Cheng, P. W. (1987). Teaching reasoning. Science, 238, 625-631.
Noori, H. (1989). The Taguchi methods: Achieving design and output quality. The Academy of Management Executive, 3, 322-326.
Nunally, J. C. (1970). Introduction to psychological measurement. New York: McGraw-Hill.
Nunnally, J. C. (1978). Psychometric theory. New York: McGraw-Hill.
Nussbaumer, H. J. (1982). Fast Fourier transforms and convolution algorithms (2nd ed.). New York: Springer-Verlag.
O'Brien, R. G., & Kaiser, M. K. (1985). MANOVA method for analyzing repeated measures designs: An extensive primer. Psychological Bulletin, 97, 316-333.
O'Neill, R. (1971). Function minimization using a Simplex procedure. Applied Statistics, 3, 79-88.
Okunade, A. A., Chang, C. F., & Evans, R. D. (1993). Comparative analysis of regression output summary statistics in common statistical packages. The American Statistician, 47, 298-303.
Olds, E. G. (1949). The 5% significance levels for sums of squares of rank differences and a correction. Annals of Mathematical Statistics, 20, 117-118.
Olejnik, S. F., & Algina, J. (1987). Type I error rates and power estimates of selected parametric and nonparametric tests of scale. Journal of Educational Statistics, 12, 45-61.
Olson, C. L. (1976). On choosing a test statistic in multivariate analysis of variance. Psychological Bulletin, 83, 579-586.
Ostle, B., & Malone, L. C. (1988). Statistics in research: Basic concepts and techniques for research workers (4th ed.). Ames, IA: Iowa State Press.
Ostrom, C. W. (1978). Time series analysis: Regression techniques. Beverly Hills, CA: Sage Publications.
Overall, J. E., & Speigel, D. K. (1969). Concerning least squares analysis of experimental data. Psychological Bulletin, 83, 579-586.
Page, E. S. (1954). Continuous inspection schemes. Biometrics, 41, 100-114.
Page, E. S. (1961). Cumulative sum charts. Technometrics, 3, 1-9.
Palumbo, F. A., & Strugala, E. S. (1945). Fraction defective of battery adapter used in handie-talkie. Industrial Quality Control, November, 68.
Pankratz, A. (1983). Forecasting with univariate Box-Jenkins models: Concepts and cases. New York: Wiley.
Parzen, E. (1961). Mathematical considerations in the estimation of spectra: Comments on the discussion of Messers, Tukey, and Goodman. Technometrics, 3, 167-190; 232-234.
Patil, K. D. (1975). Cochran's Q test: Exact distribution. Journal of the American Statistical Association, 70, 186-189.
Peace, G. S. (1993). Taguchi methods: A hands-on approach. Milwaukee, Wisconsin: ASQC.
Pearson, E. S., and Hartley, H. O. (1972). Biometrika tables for statisticians, Vol II. Cambridge: Cambridge University Press.
Pearson, K. (1894). Contributions to the mathematical theory of evolution. Philosophical Transactions of the Royal Society of London, Ser. A, 185, 71-110.
Pearson, K. (1895). Skew variation in homogeneous material. Philosophical Transactions of the Royal Society of London, Ser. A, 186, 343-414.
Pearson, K. (1896). Regression, heredity, and panmixia. Philosophical Transactions of the Royal Society of London, Ser. A, 187, 253-318.
Pearson, K. (1900). On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling. Philosophical Magazine, 5th Ser., 50, 157-175.
Pearson, K. (1904). On the theory of contingency and its relation to association and normal correlation. Drapers' Company Research Memoirs, Biometric Ser. I.
Pearson, K. (1905). Das Fehlergesetz und seine Verallgemeinerungen durch Fechner und Pearson. A Rejoinder. Biometrika, 4, 169-212.
Pearson, K. (1908). On the generalized probable error in multiple normal correlation. Biometrika, 6, 59-68.
Pearson, K., (Ed.). (1968). Tables of incomplete beta functions (2nd ed.). Cambridge, MA: Cambridge University Press.
Pedhazur, E. J. (1973). Multiple regression in behavioral research. New York: Holt, Rinehart, & Winston.
Pedhazur, E. J. (1982). Multiple regression in behavioral research (2nd ed.). New York: Holt, Rinehart, & Winston.
Peressini, A. L., Sullivan, F. E., & Uhl, J. J., Jr. (1988). The mathematics of nonlinear programming. New York: Springer.
Peto, R., & Peto, J. (1972). Asymptotically efficient rank invariant procedures. Journal of the Royal Statistical Society, 135, 185-207.
Phadke, M. S. (1989). Quality engineering using robust design. Englewood Cliffs, NJ: Prentice-Hall.
Piatetsky-Shapiro, G. (Ed.) (1993). Proceedings of AAAI- 93 Workshop on Knowledge Discovery in Databases. Menlo Park, CA: AAAI Press.
Piepel, G. F. (1988). Programs for generating extreme vertices and centroids of linearly constrained experimental regions. Journal of Quality Technology, 20, 125-139.
Piepel, G. F., & Cornell, J. A. (1994). Mixture experiment approaches: Examples, discussion, and recommendations. Journal of Quality Technology, 26, 177-196.
Pigou, A. C. (1920). Economics of Welfare. London: Macmillan.
Pike, M. C. (1966). A method of analysis of certain class of experiments in carcinogenesis. Biometrics, 22, 142-161.
Pillai, K. C. S. (1965). On the distribution of the largest characteristic root of a matrix in multivariate analysis. Biometrika, 52, 405-414.
Plackett, R. L., & Burman, J. P. (1946). The design of optimum multifactorial experiments. Biometrika, 34, 255-272.
Polya, G. (1920). Uber den zentralen Grenzwertsatz der Wahrscheinlichkeitsrechnung und das Momentenproblem. Mathematische Zeitschrift, 8, 171-181.
Porebski, O. R. (1966). Discriminatory and canonical analysis of technical college data. British Journal of Mathematical and Statistical Psychology, 19, 215-236.
Powell, M. J. D. (1964). An efficient method for finding the minimum of a function of several variables without calculating derivatives. Computer Journal, 7, 155-162.
Pregibon, D. (1997). Data Mining. Statistical Computing and Graphics, 7, 8.
Prentice, R. (1973). Exponential survivals with censoring and explanatory variables. Biometrika, 60, 279-288.
Press, William, H., Flannery, B. P., Teukolsky, S. A., Vetterling, W. T. (1986). Numerical recipies. New York: Cambridge University Press.
Press, W. H., Flannery, B. P., Teukolsky, S. A., Vetterling, W. T. (1992). Numerical recipies (2nd Edition). New York: Cambridge University Press.
Priestley, M. B. (1981). Spectral analysis and time series. New York: Academic Press.
Pyzdek, T. (1989). What every engineer should know about quality control. New York: Marcel Dekker.
Quinlan, J.R., & Cameron-Jones, R.M. (1995). Oversearching and layered search in empirical learning. Proceedings of the 14th International Joint Conference on Artificial Intelligence, Montreal (Vol. 2). Morgan Kaufman, 1019-10244.
Ralston, A., & Wilf, H.S. (Eds.). (1960). Mathematical methods for digital computers. New York: Wiley.
Ralston, A., & Wilf, H.S. (Eds.). (1967). Mathematical methods for digital computers (Vol. II). New York: Wiley.
Randles, R. H., & Wolfe, D. A. (1979). Introduction to the theory of nonparametric statistics. New York: Wiley.
Rao, C. R. (1951). An asymptotic expansion of the distribution of Wilks' criterion. Bulletin of the International Statistical Institute, 33, 177-181.
Rao, C. R. (1952). Advanced statistical methods in biometric research. New York: Wiley.
Rao, C. R. (1965). Linear statistical inference and its applications. New York: Wiley.
Rhoades, H. M., & Overall, J. E. (1982). A sample size correction for Pearson chi-square in 2 x 2 contingency tables. Psychological Bulletin, 91, 418-423.
Rinne, H., & Mittag, H. J. (1995). Statistische Methoden der Qualitatssicherung (3rd. edition). Munchen/Wien: Hanser Verlag.
Ripley, B. D. (1981). Spacial statistics. New York: Wiley.
Ripley, B. D. (1996). Pattern recognition and neural networks. Cambridge: Cambridge University Press.
Rodriguez, R. N. (1992). Recent developments in process capability analysis. Journal of Quality Technology, 24, 176-187.
Rogan, J. C., Keselman, J. J., & Mendoza, J. L. (1979). Analysis of repeated measurements. British Journal of Mathematical and Statistical Psychology, 32, 269-286.
Rosenberg, S. (1977). New approaches to the analysis of personal constructs in person perception. In A. Landfield (Ed.), Nebraska symposium on motivation (Vol. 24). Lincoln, NE: University of Nebraska Press.
Rosenberg, S., & Sedlak, A. (1972). Structural representations of implicit personality theory. In L. Berkowitz (Ed.). Advances in experimental social psychology (Vol. 6).
New York: Academic Press.
Roskam, E. E., & Lingoes, J. C. (1970). MINISSA-I: A Fortran IV program for the smallest space analysis of square symmetric matrices. Behavioral Science, 15, 204-205.
Ross, P. J. (1988). Taguchi techniques for quality engineering: Loss function, orthogonal experiments, parameter, and tolerance design. Milwaukee, Wisconsin: ASQC.
Roy, J. (1958). Step-down procedure in multivariate analysis. Annals of Mathematical Statistics, 29, 1177-1187.
Roy, J. (1967). Some aspects of multivariate analysis. New York: Wiley.
Roy, R. (1990). A primer on the Taguchi method. Milwaukee, Wisconsin: ASQC.
Royston, J. P. (1982). An extension of Shapiro and Wilk's W test for normality to large samples. Applied Statistics, 31, 115-124.
Rozeboom, W. W. (1979). Ridge regression: Bonanza or beguilement? Psychological Bulletin, 86, 242-249.
Rozeboom, W. W. (1988). Factor indeterminacy: the saga continues. British Journal of Mathematical and Statistical Psychology, 41, 209-226.
Runyon, R. P., & Haber, A. (1976). Fundamentals of behavioral statistics. Reading, MA: Addison-Wesley.
Ryan, T. P. (1989). Statistical methods for quality improvement. New York: Wiley.
Ryan, T. P. (1997). Modern Regression Methods. New York: Wiley.
Sandler, G. H. (1963). System reliability engineering. Englewood Cliffs, NJ: Prentice-Hall.
SAS Institute, Inc. (1982). SAS user's guide: Statistics, 1982 Edition. Cary, NC: SAS Institute, Inc.
Satorra, A., & Saris, W. E. (1985). Power of the likelihood ratio test in covariance structure analysis. Psychometrika, 50, 83-90.
Saxena, K. M. L., & Alam, K. (1982). Estimation of the noncentrality parameter of a chi squared distribution. Annals of Statistics, 10, 1012-1016.
Scheffe, H. (1953). A method for judging all possible contrasts in the analysis of variance. Biometrica, 40, 87-104.
Scheffe, H. (1959). The analysis of variance. New York: Wiley.
Scheffe, H. (1963). The simplex-centroid design for experiments with mixtures. Journal of the Royal Statistical Society, B25, 235-263.
Scheffe, H., & Tukey, J. W. (1944). A formula for sample sizes for population tolerance limits. Annals of Mathematical Statistics, 15, 217.
Scheines, R. (1994). Causation, indistinguishability, and regression. In F. Faulbaum, (Ed.), SoftStat '93. Advances in statistical software 4. Stuttgart: Gustav Fischer Verlag.
Schiffman, S. S., Reynolds, M. L., & Young, F. W. (1981). Introduction to multidimensional scaling: Theory, methods, and applications. New York: Academic Press.
Schmidt, P., & Muller, E. N. (1978). The problem of multicollinearity in a multistage causal alienation model: A comparison of ordinary least squares, maximum-likelihood and ridge estimators. Quality and Quantity, 12, 267-297.
Schmidt, P., & Sickles, R. (1975). On the efficiency of the Almon lag technique. International Economic Review, 16, 792-795.
Schmidt, P., & Waud, R. N. (1973). The Almon lag technique and the monetary versus fiscal policy debate. Journal of the American Statistical Association, 68, 11-19.
Schnabel, R. B., Koontz, J. E., and Weiss, B. E. (1985). A modular system of algorithms for unconstrained minimization. ACM Transactions on Mathematical Software, 11, 419-440.
Schneider, H. (1986). Truncated and censored samples from normal distributions. New York: Marcel Dekker.
Schneider, H., & Barker, G.P. (1973). Matrices and linear algebra (2nd ed.). New York: Dover Publications.
Schonemann, P. H., & Steiger, J. H. (1976). Regression component analysis. British Journal of Mathematical and Statistical Psychology, 29, 175-189.
Schrock, E. M. (1957). Quality control and statistical methods. New York: Reinhold Publishing.
Schwarz, G. ( 1978). Estimating the dimension of a model. Annals of Statistics, 6, 461-464.
Scott, D. W. (1979). On optimal and data-based histograms. Biometrika, 66, 605-610.
Searle, S. R. (1987). Linear models for unbalanced data. New York: Wiley.
Searle, S. R., Casella, G., & McCullock, C. E. (1992). Variance components.
New York: Wiley.
Seber, G. A. F., & Wild, C. J. (1989). Nonlinear regression. New York: Wiley.
Sebestyen, G. S. (1962). Decision making processes in pattern recognition. New York: Macmillan.
Sen, P. K., & Puri, M. L. (1968). On a class of multivariate multisample rank order tests, II: Test for homogeneity of dispersion matrices. Sankhya, 30, 1-22.
Shapiro, A., & Browne, M. W. (1983). On the investigation of local identifiability: A counter example. Psychometrika, 48, 303-304.
Shapiro, S. S., Wilk, M. B., & Chen, H. J. (1968). A comparative study of various tests of normality. Journal of the American Statistical Association, 63, 1343-1372.
Shewhart, W. A. (1931). Economic control of quality of manufactured product. New York: D. Van Nostrand.
Shewhart, W. A. (1939). Statistical method from the viewpoint of quality. Washington, DC: The Graduate School Department of Agriculture.
Shirland, L. E. (1993). Statistical quality control with microcomputer applications. New York: Wiley.
Shiskin, J., Young, A. H., & Musgrave, J. C. (1967). The X-11 variant of the census method II seasonal adjustment program. (Technical paper no. 15). Bureau of the Census.
Shumway, R. H. (1988). Applied statistical time series analysis. Englewood Cliffs, NJ: Prentice Hall.
Siegel, A. E. (1956). Film-mediated fantasy aggression and strength of aggressive drive. Child Development, 27, 365-378.
Siegel, S. (1956). Nonparametric statistics for the behavioral sciences. New York: McGraw-Hill.
Siegel, S., & Castellan, N. J. (1988). Nonparametric statistics for the behavioral sciences (2nd ed.) New York: McGraw-Hill.
Simkin, D., & Hastie, R. (1986). Towards an information processing view of graph perception. Proceedings of the Section on Statistical Graphics, American Statistical Association, 11-20.
Sinha, S. K., & Kale, B. K. (1980). Life testing and reliability estimation. New York: Halstead.
Smirnov, N. V. (1948). Table for estimating the goodness of fit of empirical distributions. Annals of Mathematical Statistics, 19, 279-281.
Smith, D. J. (1972). Reliability engineering. New York: Barnes & Noble.
Smith, K. (1953). Distribution-free statistical methods and the concept of power efficiency. In L. Festinger and D. Katz (Eds.), Research methods in the behavioral sciences (pp. 536-577). New York: Dryden.
Sneath, P. H. A., & Sokal, R. R. (1973). Numerical taxonomy. San Francisco: W. H. Freeman & Co.
Snee, R. D. (1975). Experimental designs for quadratic models in constrained mixture spaces. Technometrics, 17, 149-159.
Snee, R. D. (1979). Experimental designs for mixture systems with multi-component constraints. Communications in Statistics - Theory and Methods, A8(4), 303-326.
Snee, R. D. (1985). Computer-aided design of experiments - some practical experiences. Journal of Quality Technology, 17, 222-236.
Snee, R. D. (1986). An alternative approach to fitting models when re-expression of the response is useful. Journal of Quality Technology, 18, 211-225.
Sokal, R. R., & Mitchener, C. D. (1958). A statistical method for evaluating systematic relationships. University of Kansas Science Bulletin, 38, 1409.
Sokal, R. R., & Sneath, P. H. A. (1963). Principles of numerical taxonomy. San Francisco: W. H. Freeman & Co.
Soper, H. E. (1914). Tables of Poisson's exponential binomial limit. Biometrika, 10, 25-35.
Spirtes, P., Glymour, C., & Scheines, R. (1993). Causation, prediction, and search. Lecture Notes in Statistics, V. 81. New York: Springer-Verlag.
Spjotvoll, E., & Stoline, M. R. (1973). An extension of the T-method of multiple comparison to include the cases with unequal sample sizes. Journal of the American Statistical Association, 68, 976-978.
Springer, M. D. (1979). The algebra of random variables. New York: Wiley.
Spruill, M. C. (1986). Computation of the maximum likelihood estimate of a noncentrality parameter. Journal of Multivariate Analysis, 18, 216-224.
Steiger, J. H. (1979). Factor indeterminacy in the 1930's and in the 1970's; some interesting parallels. Psychometrika, 44, 157-167.
Steiger, J. H. (1980a). Tests for comparing elements of a correlation matrix. Psychological Bulletin, 87, 245-251.
Steiger, J. H. (1980b). Testing pattern hypotheses on correlation matrices: Alternative statistics and some empirical results. Multivariate Behavioral Research, 15, 335-352.
Steiger, J. H. (1988). Aspects of person-machine communication in structural modeling of correlations and covariances. Multivariate Behavioral Research, 23, 281-290.
Steiger, J. H. (1989). EzPATH: A supplementary module for SYSTAT and SYGRAPH. Evanston, IL: SYSTAT, Inc.
Steiger, J. H. (1990). Some additional thoughts on components and factors. Multivariate Behavioral Research, 25, 41-45.
Steiger, J. H., & Browne, M. W. (1984). The comparison of interdependent correlations between optimal linear composites. Psychometrika, 49, 11-24.
Steiger, J. H., & Hakstian, A. R. (1982). The asymptotic distribution of elements of a correlation matrix: Theory and application. British Journal of Mathematical and Statistical Psychology, 35, 208-215.
Steiger, J. H., & Lind, J. C. (1980). Statistically-based tests for the number of common factors. Paper presented at the annual Spring Meeting of the Psychometric Society in Iowa City. May 30, 1980.
Steiger, J. H., & Schonemann, P. H. (1978). A history of factor indeterminacy. In S. Shye, (Ed.), Theory Construction and Data Analysis in the Social Sciences. San Francisco: Jossey-Bass.
Steiger, J. H., Shapiro, A., & Browne, M. W. (1985). On the multivariate asymptotic distribution of sequential chi-square statistics. Psychometrika, 50, 253-264.
Stelzl, I. (1986). Changing causal relationships without changing the fit: Some rules for generating equivalent LISREL models. Multivariate Behavioral Research, 21, 309-331.
Stenger, F. (1973). Integration formula based on the trapezoid formula. Journal of the Institute of Mathematics and Applications, 12, 103-114.
Stevens, J. (1986). Applied multivariate statistics for the social sciences. Hillsdale, NJ: Erlbaum.
Stevens, W. L. (1939). Distribution of groups in a sequence of alternatives. Annals of Eugenics, 9, 10-17.
Stewart, D. K., & Love, W. A. (1968). A general canonical correlation index. Psychological Bulletin, 70, 160-163.
Steyer, R. (1992). Theorie causale regressionsmodelle [Theory of causal regression models]. Stuttgart: Gustav Fischer Verlag.
Steyer, R. (1994). Principles of causal modeling: a summary of its mathematical foundations and practical steps. In F. Faulbaum, (Ed.), SoftStat '93. Advances in statistical software 4. Stuttgart: Gustav Fischer Verlag.
Student (1908). The probable error of a mean. Biometrika, 6, 1-25.
Swallow, W. H., & Monahan, J. F. (1984). Monte Carlo comparison of ANOVA, MIVQUE, REML, and ML estimators of variance components. Technometrics, 26, 47-57.
Taguchi, G. (1987). Jikken keikakuho (3rd ed., Vol I & II). Tokyo: Maruzen. English translation edited by D. Clausing. System of experimental design. New York: UNIPUB/Kraus International
Tanaka, J. S., & Huba, G. J. (1985). A fit index for covariance structure models under arbitrary GLS estimation. British Journal of Mathematical and Statistical Psychology, 38, 197-201.
Tanaka, J. S., & Huba, G. J. (1989). A general coefficient of determination for covariance structure models under arbitrary GLS estimation. British Journal of Mathematical and Statistical Psychology, 42, 233-239.
Tatsuoka, M. M. (1970). Discriminant analysis. Champaign, IL: Institute for Personality and Ability Testing.
Tatsuoka, M. M. (1971). Multivariate analysis. New York: Wiley.
Tatsuoka, M. M. (1976). Discriminant analysis. In P. M. Bentler, D. J. Lettieri, and G. A. Austin (Eds.), Data analysis strategies and designs for substance abuse research. Washington, DC: U.S. Government Printing Office.
Thorndyke, R. L., & Hagen, E. P. (1977). Measurement and evaluation in psychology and education. New York: Wiley.
Thurstone, L. L. (1931). Multiple factor analysis. Psychological Review, 38, 406-427.
Thurstone, L. L. (1947). Multiple factor analysis. Chicago: University of Chicago Press.
Timm, N. H. (1975). Multivariate analysis with applications in education and psychology. Monterey, CA: Brooks/Cole.
Timm, N. H., & Carlson, J. (1973). Multivariate analysis of non-orthogonal experimental designs using a multivariate full rank model. Paper presented at the American Statistical Association Meeting, New York.
Timm, N. H., & Carlson, J. (1975). Analysis of variance through full rank models. Multivariate behavioral research monographs, No. 75-1.
Tracey, N. D., Young, J., C., & Mason, R. L. (1992). Multivariate control charts for individual observations. Journal of Quality Technology, 2, 88-95.
Tribus, M., & Sconyi, G. (1989). An alternative view of the Taguchi approach. Quality Progress, 22, 46-48.
Trivedi, P. K., & Pagan, A. R. (1979). Polynomial distributed lags: A unified treatment. Economic Studies Quarterly, 30, 37-49.
Tryon, R. C. (1939). Cluster Analysis. Ann Arbor, MI: Edwards Brothers.
Tucker, L. R., Koopman, R. F., & Linn, R. L. (1969). Evaluation of factor analytic research procedures by means of simulated correlation matrices. Psychometrika, 34, 421-459.
Tufte, E. R. (1983). The visual display of quantitative information. Cheshire, CT: Graphics Press.
Tufte, E. R. (1990). Envisioning information. Cheshire, CT: Graphics Press.
Tukey, J. W. (1953). The problem of multiple comparisons. Unpublished manuscript, Princeton University.
Tukey, J. W. (1962). The future of data analysis. Annals of Mathematical Statistics, 33, 1-67.
Tukey, J. W. (1967). An introduction to the calculations of numerical spectrum analysis. In B. Harris (Ed.), Spectral analysis of time series. New York: Wiley.
Tukey, J. W. (1972). Some graphic and semigraphic displays. In Statistical Papers in Honor of George W. Snedecor; ed. T. A. Bancroft, Arnes, IA: Iowa State University Press, 293-316.
Tukey, J. W. (1977). Exploratory data analysis.
Reading, MA: Addison-Wesley.
Tukey, J. W. (1984). The collected works of John W. Tukey. Monterey, CA: Wadsworth.
Tukey, P. A. (1986). A data analyst's view of statistical plots. Proceedings of the Section on Statistical Graphics, American Statistical Association, 21-28.
Tukey, P. A., & Tukey, J. W. (1981). Graphical display of data sets in 3 or more dimensions. In V. Barnett (Ed.), Interpreting multivariate data. Chichester, U.K.: Wiley.
Upsensky, J. V. (1937). Introduction to Mathematical Probability. New York: McGraw-Hill.
Vale, C. D., & Maurelli, V. A. (1983). Simulating multivariate non-normal distributions. Psychometrika, 48, 465-471.
Vandaele, W. (1983). Applied time series and Box-Jenkins models. New York: Academic Press.
Vaughn, R. C. (1974). Quality control. Ames, IA: Iowa State Press.
Velicer, W. F., & Jackson, D. N. (1990). Component analysis vs. factor analysis: some issues in selecting an appropriate procedure. Multivariate Behavioral Research, 25, 1-28.
Velleman, P. F., & Hoaglin, D. C. (1981). Applications, basics, and computing of exploratory data analysis. Belmont, CA: Duxbury Press.
Von Mises, R. (1941). Grundlagen der Wahrscheinlichkeitsrechnung. Mathematische Zeitschrift, 5, 52-99.
Wainer, H. (1995). Visual revelations. Chance, 8, 48-54.
Wald, A. (1939). Contributions to the theory of statistical estimation and testing hypotheses. Annals of Mathematical Statistics, 10, 299-326.
Wald, A. (1945). Sequential tests of statistical hypotheses. Annals of Mathematical Statistics, 16, 117-186.
Wald, A. (1947). Sequential analysis. New York: Wiley.
Walker, J. S. (1991). Fast Fourier transforms. Boca Raton, FL: CRC Press.
Wallis, K. F. (1974). Seasonal adjustment and relations between variables. Journal of the American Statistical Association, 69, 18-31.
Wang, C. M., & Gugel, H. W. (1986). High-performance graphics for exploring multivariate data. Proceedings of the Section on Statistical Graphics, American Statistical Association, 60-65.
Ward, J. H. (1963). Hierarchical grouping to optimize an objective function. Journal of the American Statistical Association, 58, 236.
Warner B. & Misra, M. (1996). Understanding Neural Networks as Statistical Tools. The American Statistician, 50, 284-293.
Weatherburn, C. E. (1946). A First Course in Mathematical Statistics. Cambridge: Cambridge University Press.
Wei, W. W. (1989). Time series analysis: Univariate and multivariate methods. New York: Addison-Wesley.
Weibull, W., (1939). A statistical theory of the strength of materials. Ing. Velenskaps Akad. Handl., 151, 1-45.
Weibull, W. (1951). A statistical distribution function of wide applicability. Journal of Applied Mechanics, September.
Welch, B. L. (1938). The significance of the differences between two means when the population variances are unequal. Biometrika, 29, 350-362.
Welstead, S. T. (1994). Neural network and fuzzy logic applications in C/C++. New York: Wiley.
Wescott, M. E. (1947). Attribute charts in quality control. Conference Papers, First Annual Convention of the American Society for Quality Control. Chicago: John S. Swift Co.
Wheaton, B., Muthen, B., Alwin, D., & Summers G. (1977). Assessing reliability and stability in panel models. In D. R. Heise (Ed.), Sociological Methodology. New York: Wiley.
Wheeler, D. J., & Chambers, D.S. (1986). Understanding statistical process control. Knoxville, TN: Statistical Process Controls, Inc.
Wherry, R. J. (1984). Contributions to correlational analysis. New York: Academic Press.
Whitney, D. R. (1948). A comparison of the power of non-parametric tests and tests based on the normal distribution under non-normal alternatives. Unpublished doctoral dissertation, Ohio State University.
Whitney, D. R. (1951). A bivariate extension of the U statistic. Annals of Mathematical Statistics, 22, 274-282.
Wiggins, J. S., Steiger, J. H., and Gaelick, L. (1981). Evaluating circumplexity in models of personality. Multivariate Behavioral Research, 16, 263-289.
Wilcoxon, F. (1945). Individual comparisons by ranking methods. Biometrica Bulletin, 1, 80-83.
Wilcoxon, F. (1947). Probability tables for individual comparisons by ranking methods. Biometrics, 3, 119-122.
Wilcoxon, F. (1949). Some rapid approximate statistical procedures. Stamford, CT: American Cyanamid Co.
Wilde, D. J., & Beightler, C. S. (1967). Foundations of optimization. Englewood Cliffs, NJ: Prentice-Hall.
Wilks, S. S. (1943). Mathematical Statistics. Princeton, NJ: Princeton University Press.
Wilks, S. S. (1946). Mathematical statistics. Princeton, NJ: Princeton University Press.
Williams, W. T., Lance, G. N., Dale, M. B., & Clifford, H. T. (1971). Controversy concerning the criteria for taxonometric strategies. Computer Journal, 14, 162.
Wilson, G. A., & Martin, S. A. (1983). An empirical comparison of two methods of testing the significance of a correlation matrix. Educational and Psychological Measurement, 43, 11-14.
Winer, B. J. (1962). Statistical principles in experimental design. New York: McGraw-Hill.
Winer, B. J. (1971). Statistical principles in experimental design (2nd ed.). New York: McGraw-Hill.
Winer, B. J. (1971). Statistical principles in experimental design (2nd ed.). New York: McGraw Hill.
Wolfowitz, J. (1942). Additive partition functions and a class of statistical hypotheses. Annals of Mathematical Statistics, 13, 247-279.
Wolynetz, M. S. (1979a). Maximum likelihood estimation from confined and censored normal data. Applied Statistics, 28, 185-195.
Wolynetz, M. S. (1979b). Maximum likelihood estimation in a linear model from confined and censored normal data. Applied Statistics, 28, 195-206.
Wonnacott, R. J., & Wonnacot, T. H. (1970). Econometrics. New York: Wiley.
Woodward, J. A., Bonett, D. G., & Brecht, M. L. (1990). Introduction to linear models and experimental design. New York: Harcourt, Brace, Jovanovich.
Woodward, J. A., & Overall, J. E. (1975). Multivariate analysis of variance by multiple regression methods. Psychological Bulletin, 82, 21-32.
Woodward, J. A., & Overall, J. E. (1976). Calculation of power of the F test. Educational and Psychological Measurement, 36, 165-168.
Woodward, J. A., Douglas, G. B., & Brecht, M. L. (1990). Introduction to linear models and experimental design. New York: Academic Press.
Yates, F. (1933). The principles of orthogonality and confounding in replicated experiments. Journal of Agricultural Science, 23, 108-145.
Yates, F. (1937). The Design and Analysis of Factorial Experiments. Imperial Bureau of Soil Science, Technical Communication No. 35, Harpenden.
Yokoyama, Y., & Taguchi, G. (1975). Business data analysis: Experimental regression analysis. Tokyo: Maruzen.
Youden, W. J., & Zimmerman, P. W. (1936). Field trials with fiber pots. Contributions from Boyce Thompson Institute, 8, 317-331.
Young, F. W, & Hamer, R. M. (1987). Multidimensional scaling: History, theory, and applications. Hillsdale, NJ: Erlbaum
Young, F. W., Kent, D. P., & Kuhfeld, W. F. (1986). Visuals: Software for dynamic hyper-dimensional graphics. Proceedings of the Section on Statistical Graphics, American Statistical Association, 69-74.
Younger, M. S. (1985). A first course in linear regression (2nd ed.). Boston: Duxbury Press.
Yuen, C. K., & Fraser, D. (1979). Digital spectral analysis. Melbourne: CSIRO/Pitman.
Yule, G. U. (1897). On the theory of correlation. Journal of the Royal Statistical Society, 60, 812-854.
Yule, G. U. (1907). On the theory of correlation for any number of variables treated by a new system of notation. Proceedings of the Royal Society, Ser. A, 79, 182-193.
Yule, G. U. (1911). An Introduction to the Theory of Statistics. London: Griffin.
Zippin, C., & Armitage, P. (1966). Use of concomitant variables and incomplete survival information in the estimation of an exponential survival parameter. Biometrics, 22, 665-672.
Zupan, J. (1982). Clustering of large data sets. New York: Research Studies Press.
Zwick, W. R., & Velicer, W. F.(1986). Comparison of five rules for determining the number of components to retain. Psychological Bulletin, 99, 432-442.

© Copyright StatSoft, Inc., 1984-2001
STATISTICA является торговой маркой StatSoft, Inc.
Электронный учебник по промышленной статистике
| Электронный учебник по промышленной статистике помогает начинающим пользователям получить базовые знания по контролю качества, анализу процессов и планированию экспериментов на производстве. По многочисленным просьбам наших клиентов, в книгу включен раздел по основам внедрения ISO 9000. Материал учебника был подготовлен отделом распространения и технической поддержки компании StatSoft на основе многолетнего опыта решения производственных задач и чтения лекций пользователям STATISTICA. В пособии приводится большое количество примеров уже решенных задач с использованием методов промышленной статистики, а также отчеты, предоставленные нашими партнерами, которые успешно используют STATISTICA в своей производственной деятельности. |
| В учебнике детально рассмотрены методы промышленной статистики и реализация их с помощью программных продуктов серии STATISTICA. Включены материалы по методике внедрения ISO 9000. Подробно обсуждаются некоторые специфические требования ISO 9000, связанные со статистическим контролем процессов (SPC), а так же объясняются способы решения проблем SPC на STATISTICA. Описание различных областей организовано в виде текстовых "модулей". Каждый такой модуль соответствует определенному классу методов промышленной статистики. |
| В разделе «Примеры проектов» рассматриваются решения типовых производственных задач, связанных с контролем качества. В основном, - это отчеты менеджеров по качеству, выполненные в форме: проблема, варианты решения, результаты. В конце приводятся комментарии наших технических специалистов. Мы планируем регулярно дополнять этот раздел новыми материалами. Подробное руководство по основным модулям STATISTICA можно посмотреть здесь: |
| При использовании материалов данного учебника обязательна ссылка на него следующего вида: StatSoft, Inc. (2001). Электронный учебник по промышленной статистике. Москва, StatSoft. WEB: http://www.statsoft.ru/home/portal/textbook_ind/default.htm. |

STATISTICA является торговой маркой StatSoft, Inc.