Нейронные сети

Нейронные сети

Введение Параллели из биологии Базовая искусственная модель Применение нейронных сетей Сбор данных для нейронной сети Выводы Пре/пост процессирование Многослойный персептрон (MLP) Обучение многослойного персептрона Алгоритм обратного распространения Переобучение и обобщение Отбор данных Как обучается многослойный персептрон Другие алгоритмы обучения многослойного персептрона Радиальная базисная функция Вероятностная нейронная сеть Обобщенно-регрессионная нейронная сеть Линейная сеть Сеть Кохонена Решение задач классификации в пакете ST: Neural Networks Таблица статистик классификации Решение задач регрессии в пакете ST: Neural Networks Прогнозирование временных рядов в пакете ST: Neural Networks Отбор переменных и понижение размерности

Многие понятия, относящиеся к методам нейронных сетей, лучше всего объяснять на примере конкретной нейронно-сетевой программы. Поэтому в данном разделе будет много ссылок на пакет STATISTICA Neural Networks ( сокращенно, ST Neural Networks, нейронно-сетевой пакет фирмы StatSoft), представляющий собой реализацию всего набора нейросетевых методов анализа данных.
Введение Параллели из биологии Базовая искусственная модель Применение нейронных сетей Сбор данных для нейронной сети Выводы Пре/пост процессирование Многослойный персептрон (MLP) Обучение многослойного персептрона Алгоритм обратного распространения Переобучение и обобщение Отбор данных Как обучается многослойный персептрон Другие алгоритмы обучения многослойного персептрона Радиальная базисная функция Вероятностная нейронная сеть Обобщенно-регрессионная нейронная сеть Линейная сеть Сеть Кохонена Решение задач классификации в пакете ST: Neural Networks Таблица статистик классификации Решение задач регрессии в пакете ST: Neural Networks Прогнозирование временных рядов в пакете ST: Neural Networks Отбор переменных и понижение размерности

Многие понятия, относящиеся к методам нейронных сетей, лучше всего объяснять на примере конкретной нейронно-сетевой программы.
Поэтому в данном разделе будет много ссылок на пакет STATISTICA Neural Networks ( сокращенно, ST Neural Networks, нейронно-сетевой пакет фирмы StatSoft), представляющий собой реализацию всего набора нейросетевых методов анализа данных.

Введение
Введение

В последние несколько лет мы наблюдаем взрыв интереса к нейронным сетям, которые успешно применяются в самых различных областях - бизнесе, медицине, технике, геологии , физике. Нейронные сети вошли в практику везде, где нужно решать задачи прогнозирования, классификации или управления. Такой впечатляющий успех определяется несколькими причинами: Богатые возможности. Нейронные сети - исключительно мощный метод моделирования, позволяющий воспроизводить чрезвычайно сложные зависимости. В частности, нейронные сети нелинейны по свой природе (смысл этого понятия подробно разъясняется далее в этой главе). На протяжение многих лет линейное моделирование было основным методом моделирования в большинстве областей, поскольку для него хорошо разработаны процедуры оптимизации. В задачах, где линейная аппроксимация неудовлетворительна (а таких достаточно много), линейные модели работают плохо. Кроме того, нейронные сети справляются с "проклятием размерности", которое не позволяет моделировать линейные зависимости в случае большого числа переменных Простота в использовании.  Нейронные сети учатся на примерах. Пользователь нейронной сети подбирает представительные данные, а затем запускает алгоритм обучения, который автоматически воспринимает структуру данных. При этом от пользователя, конечно, требуется какой-то набор эвристических знаний о том, как следует отбирать и подготавливать данные, выбирать нужную архитектуру сети и интерпретировать результаты, однако уровень знаний, необходимый для успешного применения нейронных сетей, гораздо скромнее, чем, например, при использовании традиционных методов статистики. Нейронные сети привлекательны с интуитивной точки зрения, ибо они основаны на примитивной биологической модели нервных систем.


В будущем развитие таких нейро-биологических моделей может привести к созданию действительно мыслящих компьютеров. Между тем уже "простые" нейронные сети, которые строит система ST Neural Networks , являются мощным оружием в арсенале специалиста по прикладной статистике.

В начало

Параллели из биологии
Параллели из биологии

Нейронные сети возникли из исследований в области искусственного интеллекта, а именно, из попыток воспроизвести способность биологических нервных систем обучаться и исправлять ошибки, моделируя низкоуровневую структуру мозга (Patterson, 1996). Основной областью исследований по искусственному интеллекту в 60-е - 80-е годы были экспертные системы. Такие системы основывались на высокоуровневом моделировании процесса мышления (в частности, на представлении, что процесс нашего мышления построен на манипуляциях с символами). Скоро стало ясно, что подобные системы, хотя и могут принести пользу в некоторых областях, не ухватывают некоторые ключевые аспекты человеческого интеллекта. Согласно одной из точек зрения, причина этого состоит в том, что они не в состоянии воспроизвести структуру мозга. Чтобы создать искусственных интеллект, необходимо построить систему с похожей архитектурой. Мозг состоит из очень большого числа (приблизительно 10,000,000,000) нейронов, соединенных многочисленными связями (в среднем несколько тысяч связей на один нейрон, однако это число может сильно колебаться). Нейроны - это специальная клетки, способные распространять электрохимические сигналы. Нейрон имеет разветвленную структуру ввода информации (дендриты), ядро и разветвляющийся выход (аксон). Аксоны клетки соединяются с дендритами других клеток с помощью синапсов. При активации нейрон посылает электрохимический сигнал по своему аксону. Через синапсы этот сигнал достигает других нейронов, которые могут в свою очередь активироваться. Нейрон активируется тогда, когда суммарный уровень сигналов, пришедших в его ядро из дендритов, превысит определенный уровень (порог активации).



.Интенсивность сигнала, получаемого нейроном (а следовательно и возможность его активации), сильно зависит от активности синапсов. Каждый синапс имеет протяженность, и специальные химические вещества передают сигнал вдоль него. Один из самых авторитетных исследователей нейросистем, Дональд Хебб, высказал постулат, что обучение заключается в первую очередь в изменениях "силы" синаптических связей. Например, в классическом опыте Павлова, каждый раз непосредственно перед кормлением собаки звонил колокольчик, и собака быстро научилась связывать звонок колокольчика с пищей. Синаптические связи между участками коры головного мозга, ответственными за слух, и слюнными железами усилились, и при возбуждении коры звуком колокольчика у собаки начиналось слюноотделение.

Таким образом, будучи построен из очень большого числа совсем простых элементов (каждый из которых берет взвешенную сумму входных сигналов и в случае, если суммарный вход превышает определенный уровень, передает дальше двоичный сигнал), мозг способен решать чрезвычайно сложные задачи. Разумеется, мы не затронули здесь многих сложных аспектов устройства мозга, однако интересно то, что искусственные нейронные сети способны достичь замечательных результатов, используя модель, которая ненамного сложнее, чем описанная выше.

В начало

Базовая искусственная модель
Базовая искусственная модель

Чтобы отразить суть биологических нейронных систем, определение искусственного нейрона дается следующим образом: Он получает входные сигналы (исходные данные либо выходные сигналы других нейронов нейронной сети) через несколько входных каналов. Каждый входной сигнал проходит через соединение, имеющее определенную интенсивность (или вес); этот вес соответствует синаптической активности биологического нейрона. С каждым нейроном связано определенное пороговое значение. Вычисляется взвешенная сумма входов, из нее вычитается пороговое значение и в результате получается величина активации нейрона (она также называется пост-синаптическим потенциалом нейрона - PSP). Сигнал активации преобразуется с помощью функции активации (или передаточной функции) и в результате получается выходной сигнал нейрона. .Если при этом использовать ступенчатую функцию активации (т.е., выход нейрона равен нулю, если вход отрицательный, и единице, если вход нулевой или положительный), то такой нейрон будет работать точно так же, как описанный выше естественный нейрон (вычесть пороговое значение из взвешенной суммы и сравнить результат с нулем - это то же самое, что сравнить взвешенную сумму с пороговым значением).


В действительности, как мы скоро увидим, пороговые функции редко используются в искусственных нейронных сетях. Учтите, что веса могут быть отрицательными, - это значит, что синапс оказывает на нейрон не возбуждающее, а тормозящее воздействие (в мозге присутствуют тормозящие нейроны). Это было описание отдельного нейрона. Теперь возникает вопрос: как соединять нейроны друг с другом? Если сеть предполагается для чего-то использовать, то у нее должны быть входы (принимающие значения интересующих нас переменных из внешнего мира) и выходы (прогнозы или управляющие сигналы). Входы и выходы соответствуют сенсорным и двигательным нервам - например, соответственно, идущим от глаз и в руки. Кроме этого, однако, в сети может быть еще много промежуточных (скрытых) нейронов, выполняющих внутренние функции. Входные, скрытые и выходные нейроны должны быть связаны между собой.

Ключевой вопрос здесь - обратная связь (Haykin, 1994). Простейшая сеть имеет структуру прямой передачи сигнала: Сигналы проходят от входов через скрытые элементы и в конце концов приходят на выходные элементы. Такая структура имеет устойчивое поведение. Если же сеть рекуррентная (т.е. содержит связи, ведущие назад от более дальних к более ближним нейронам), то она может быть неустойчива и иметь очень сложную динамику поведения. Рекуррентные сети представляют большой интерес для исследователей в области нейронных сетей, однако при решении практических задач, по крайней мере до сих пор, наиболее полезными оказались структуры прямой передачи, и именно такой тип нейронных сетей моделируется в пакете ST Neural Networks.

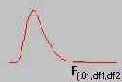
.Типичный пример сети с прямой передачей сигнала показан на рисунке. Нейроны регулярным образом организованы в слои. Входной слой служит просто для ввода значений входных переменных. Каждый из скрытых и выходных нейронов соединен со всеми элементами предыдущего слоя. Можно было бы рассматривать сети, в которых нейроны связаны только с некоторыми из нейронов предыдущего слоя; однако, для большинства приложений сети с полной системой связей предпочтительнее, и именно такой тип сетей реализован в пакете ST Neural Networks.





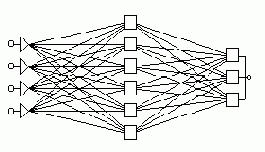
При работе (использовании) сети во входные элементы подаются значения входных переменных, затем последовательно отрабатывают нейроны промежуточных и выходного слоев. Каждый из них вычисляет свое значение активации, беря взвешенную сумму выходов элементов предыдущего слоя и вычитая из нее пороговое значение. Затем значение активации преобразуются с помощью функции активации, и в результате получается выход нейрона. После того, как вся сеть отработает, выходные значения элементов выходного слоя принимаются за выход всей сети в целом.

В начало

Применение нейронных сетей
Применение нейронных сетей

В предыдущем разделе в несколько упрощенном виде было описано, как нейронная сеть преобразует входные сигналы в выходные. Теперь возникает следующий важный вопрос: как применить нейронную сеть к решению конкретной задачи? Класс задач, которые можно решить с помощью нейронной сети, определяется тем, как сеть работает и тем, как она обучается. При работе нейронная сеть принимает значения входных переменных и выдает значения выходных переменных. Таким образом, сеть можно применять в ситуации, когда у Вас имеется определенная известная информация, и Вы хотите из нее получить некоторую пока не известную информацию (Patterson, 1996; Fausett, 1994). Вот некоторые примеры таких задач:

Прогнозирование на фондовом рынке.
Прогнозирование на фондовом рынке.

Зная цены акций за последнюю неделю и сегодняшнее значение индекса FTSE, спрогнозировать завтрашнюю цену акций.

Предоставление кредита.
Предоставление кредита.

Требуется определить, высок ли риск предоставления кредита частному лицу, обратившемуся с такой просьбой. В результате разговора с ним известен его доход, предыдущая кредитная история и т.д.

Управление.
Управление.

Нужно определить что должен делать робот (повернуться направо или налево, двигаться вперед и т.д.), чтобы достичь цели; известно изображение, которое передает установленная на роботе видеокамера.

Разумеется, вовсе не любую задачу можно решить с помощью нейронной сети.


Если Вы хотите определить результаты лотереи, тираж которой состоится через неделю, зная свой размер обуви, то едва ли это получится, поскольку эти вещи не связаны друг с другом. На самом деле, если тираж проводится честно, то не существует такой информации, на основании которой можно было бы предсказать результат. Многие финансовые структуры уже используют нейронные сети или экспериментируют с ними с целью прогнозирования ситуации на фондовом рынке, и похоже, что любой тренд, прогнозируемый с помощью нейронных методов, всякий раз уже бывает "дисконтирован" рынком, и поэтому (к сожалению) эту задачу Вам тоже вряд ли удастся решить.

Итак, мы приходим ко второму важному условию применения нейронных сетей: Вы должны знать (или хотя бы иметь серьезные подозрения), что между известными входными значениями и неизвестными выходами имеется связь. Эта связь может быть искажена шумом (так, едва ли можно ожидать, что по данным из примера с прогнозированием цен акций можно построить абсолютно точный прогноз, поскольку на цену влияют и другие факторы, не представленные во входном наборе данных, и кроме того в задаче присутствует элемент случайности), но она должна существовать.

Как правило, нейронная сеть используется тогда, когда неизвестен точный вид связей между входами и выходами, - если бы он был известен, то связь можно было бы моделировать непосредственно. Другая существенная особенность нейронных сетей состоит в том, что зависимость между входом и выходом находится в процессе обучения сети. Для обучения нейронных сетей применяются алгоритмы двух типов (разные типы сетей используют разные типы обучения): управляемое ("обучение с учителем") и не управляемое ("без учителя"). Чаще всего применяется обучение с учителем, и именно этот метод мы сейчас рассмотрим (о неуправляемом обучении будет рассказано позже).

Для управляемого обучения сети пользователь должен подготовить набор обучающих данных. Эти данные представляют собой примеры входных данных и соответствующих им выходов.


Сеть учится устанавливать связь между первыми и вторыми. Обычно обучающие данные берутся из исторических сведений. В рассмотренных выше примерах это могут быть предыдущие значения цен акций и индекса FTSE, сведения о прошлых заемщиках - их анкетные данные и то, успешно ли они выполнили свои обязательства, примеры положений робота и его правильной реакции.

Затем нейронная сеть обучается с помощью того или иного алгоритма управляемого обучения (наиболее известным из них является метод обратного распространения, предложенный в работе Rumelhart et al., 1986), при котором имеющиеся данные используются для корректировки весов и пороговых значений сети таким образом, чтобы минимизировать ошибку прогноза на обучающем множестве. Если сеть обучена хорошо, она приобретает способность моделировать (неизвестную) функцию, связывающую значения входных и выходных переменных, и впоследствии такую сеть можно использовать для прогнозирования в ситуации, когда выходные значения неизвестны.

В начало

Сбор данных для нейронной сети
Сбор данных для нейронной сети

Если задача будет решаться с помощью нейронной сети, то необходимо собрать данные для обучения. Обучающий набор данных представляет собой набор наблюдений, для которых указаны значения входных и выходных переменных. Первый вопрос, который нужно решить, - какие переменные использовать и сколько (и каких) наблюдений собрать. Выбор переменных (по крайней мере первоначальный) осуществляется интуитивно. Ваш опыт работы в данной предметной области поможет определить, какие переменные являются важными. При работе с пакетом ST Neural Networks Вы можете произвольно выбирать переменные и отменять предыдущий выбор; кроме того, система ST Neural Networks умеет сама опытным путем отбирать полезные переменные. Для начала имеет смысл включить все переменные, которые, по Вашему мнению, могут влиять на результат - на последующих этапах мы сократим это множество.

Нейронные сети могут работать с числовыми данными, лежащими в определенном ограниченном диапазоне.


Это создает проблемы в случаях, когда данные имеют нестандартный масштаб, когда в них имеются пропущенные значения, и когда данные являются нечисловыми. В пакете ST Neural Networks имеются средства, позволяющие справиться со всеми этими трудностями. Числовые данные масштабируются в подходящий для сети диапазон, а пропущенные значения можно заменить на среднее значение (или на другую статистику) этой переменной по всем имеющимся обучающим примерам (Bishop, 1995).

Более трудной задачей является работа с данными нечислового характера. Чаще всего нечисловые данные бывают представлены в виде номинальных переменных типа Пол = {Муж , Жен }. Переменные с номинальными значениями можно представить в числовом виде, и в системе ST Neural Networks имеются средства для работы с такими данными. Однако, нейронные сети не дают хороших результатов при работе с номинальными переменными, которые могут принимать много разных значений.

Пусть, например, мы хотим научить нейронную сеть оценивать стоимость объектов недвижимости. Цена дома очень сильно зависит от того, в каком районе города он расположен. Город может быть подразделен на несколько десятков районов, имеющих собственные названия, и кажется естественным ввести для обозначения района переменную с номинальными значениями. К сожалению, в этом случае обучить нейронную сеть будет очень трудно, и вместо этого лучше присвоить каждому району определенный рейтинг (основываясь на экспертных оценках).

Нечисловые данные других типов можно либо преобразовать в числовую форму, либо объявить незначащими. Значения дат и времени, если они нужны, можно преобразовать в числовые, вычитая из них начальную дату (время). Обозначения денежных сумм преобразовать совсем несложно. С произвольными текстовыми полями (например, фамилиями людей) работать нельзя и их нужно сделать незначащими.

Вопрос о том, сколько наблюдений нужно иметь для обучения сети, часто оказывается непростым. Известен ряд эвристических правил, увязывающих число необходимых наблюдений с размерами сети (простейшее из них гласит, что число наблюдений должно быть в десять раз больше числа связей в сети).


На самом деле это число зависит также от (заранее неизвестной) сложности того отображения, которое нейронная сеть стремится воспроизвести. С ростом количества переменных количество требуемых наблюдений растет нелинейно, так что уже при довольно небольшом (например, пятьдесят) числе переменных может потребоваться огромное число наблюдений. Эта трудность известна как "проклятие размерности", и мы обсудим ее дальше в этой главе.

Для большинства реальных задач бывает достаточно нескольких сотен или тысяч наблюдений. Для особо сложных задач может потребоваться еще большее количество, однако очень редко может встретиться (даже тривиальная) задача, где хватило бы менее сотни наблюдений. Если данных меньше, чем здесь сказано, то на самом деле у Вас недостаточно информации для обучения сети, и лучшее, что Вы можете сделать - это попробовать подогнать к данным некоторую линейную модель. В пакете ST Neural Networks реализованы средства для подгонки линейных моделей (см. раздел про линейные сети, а также материал по модулю Множественная регрессия системы STATISTICA).

Во многих реальных задачах приходится иметь дело с не вполне достоверными данными. Значения некоторых переменных могут быть искажены шумом или частично отсутствовать. Пакет ST Neural Networks имеет специальные средства работы с пропущенными значениями (они могут быть заменены на среднее значение этой переменной или на другие ее статистики), так что если у Вас не так много данных, Вы можете включить в рассмотрение случаи с пропущенными значениями (хотя, конечно, лучше этого избегать). Кроме того, нейронные сети в целом устойчивы к шумам. Однако у этой устойчивости есть предел. Например, выбросы, т.е. значения, лежащие очень далеко от области нормальных значений некоторой переменной, могут исказить результат обучения. В таких случаях лучше всего постараться обнаружить и удалить эти выбросы (либо удалив соответствующие наблюдения, либо преобразовав выбросы в пропущенные значения). Если выбросы выявить трудно, то можно воспользоваться имеющимися в пакете ST Neural Networks возможностями сделать процесс обучения устойчивым к выбросам (с помощью функции ошибок типа "городских кварталов"; см.


Bishop, 1995), однако такое устойчивое к выбросам обучение, как правило, менее эффективно, чем стандартное.

Выводы
Выводы

Выбирайте такие переменные, которые, как Вы предполагаете, влияют на результат.

С числовыми и номинальными переменными в пакете ST Neural Networks можно работать непосредственно. Переменные других типов следует преобразовать в указанные типы или объявить незначащими.

Для анализа нужно иметь порядка сотен или тысяч наблюдений; чем больше в задаче переменных, тем больше нужно иметь наблюдений. Пакет ST Neural Networks имеет средства для распознавания значимых переменных, поэтому включайте в рассмотрение переменные, в значимости которых Вы не уверены.

В случае необходимости можно работать с наблюдениями, содержащими пропущенные значения. Наличие выбросов в данных может создать трудности. Если возможно, удалите выбросы. Если данных достаточное количество, уберите из рассмотрения наблюдения с пропущенными значениями.

В начало

Пре/пост процессирование
Пре/пост процессирование

Всякая нейронная сеть принимает на входе числовые значения и выдает на выходе также числовые значения. Передаточная функция для каждого элемента сети обычно выбирается таким образом, чтобы ее входной аргумент мог принимать произвольные значения, а выходные значения лежали бы в строго ограниченном диапазоне ("сплющивание"). При этом, хотя входные значения могут быть любыми, возникает эффект насыщения, когда элемент оказывается чувствительным лишь к входным значениям, лежащим в некоторой ограниченной области. На этом рисунке представлена одна из наиболее распространенных передаточных функций - так называемая логистическая функция (иногда ее также называют сигмоидной функцией, хотя если говорить строго, это всего лишь один из частных случаев сигмоидных - т.е. имеющих форму буквы S - функций). В этом случае выходное значение всегда будет лежать в интервале (0,1), а область чувствительности для входов чуть шире интервала (-1,+1). Данная функция является гладкой, а ее производная легко вычисляется - это обстоятельство весьма существенно для работы алгоритма обучения сети (в этом также кроется причина того, что ступенчатая функция для этой цели практически не используется).



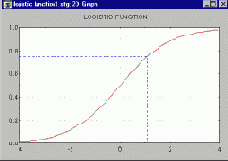
Коль скоро выходные значения всегда принадлежат некоторой ограниченной области, а вся информация должна быть представлена в числовом виде, очевидно, что при решении реальных задач методами нейронных сетей требуются этапы предварительной обработки - пре-процессирования - и заключительной обработки - пост-процессирования данных (Bishop, 1995). Соответствующие средства имеются в пакете ST Neural Networks. Здесь нужно рассмотреть два вопроса:

Шкалирование.
Шкалирование.

Числовые значения должны быть приведены в масштаб, подходящий для сети. Обычно исходные данные масштабируются по линейной шкале. В пакете ST Neural Networks реализованы алгоритмы минимакса и среднего/стандартного отклонения, которые автоматически находят масштабирующие параметры для преобразования числовых значений в нужный диапазон.

В некоторых случаях более подходящим может оказаться нелинейное шкалирование (например, если заранее известно, что переменная имеет экспоненциальное распределение, имеет смысл взять ее логарифм). Нелинейное шкалирование не реализовано в модуле ST Neural Networks. Вы можете прошкалировать переменную средствами преобразования даных базовой системы STATISTICA, а затем работать с ней в модуле ST Neural Networks.

Номинальные переменные.
Номинальные переменные.

Номинальные переменные могут быть двузначными (например, Пол ={Муж, Жен}) или многозначными (т.е. принимать более двух значений или состояний). Двузначную номинальную переменную легко преобразовать в числовую (например, Муж = 0, Жен = 1). С многозначными номинальными переменными дело обстоит сложнее. Их тоже можно представить одним числовым значением (например, Собака = 0, Овца = 1, Кошка = 2), однако при этом возникнет (возможно) ложное упорядочивание значений номинальной переменной: в рассмотренном примере Овца окажется чем-то средним между Собакой и Кошкой. Существует более точный способ, известный как кодирование 1-из-N, в котором одна номинальная переменная представляется несколькими числовыми переменными.


Количество числовых переменных равно числу возможных значений номинальной переменной; при этом всякий раз ровно одна из N переменных принимает ненулевое значение (например, Собака = {1,0,0}, Овца = {0,1,0}, Кошка = {0,0,1}). В пакете ST Neural Networks имеются возможности преобразовывать как двух-, так и многозначные номинальные переменные для последующего использования в нейронной сети. К сожалению, номинальная переменная с большим числом возможных состояний потребует при кодировании методом 1-из-N очень большого количества числовых переменных, а это приведет к росту размеров сети и создаст трудности при ее обучении. В таких ситуациях возможно (но не всегда достаточно) смоделировать номинальную переменную с помощью одного числового индекса, однако лучше будет попытаться найти другой способ представления данных.

Задачи прогнозирования можно разбить на два основных класса: классификация и регрессия.

В задачах классификации нужно бывает определить, к какому из нескольких заданных классов принадлежит данный входной набор. Примерами могут служить предоставление кредита (относится ли данное лицо к группе высокого или низкого кредитного риска), диагностика раковых заболеваний (опухоль, чисто), распознавание подписи (поддельная, подлинная). Во всех этих случаях, очевидно, на выходе требуется всего одна номинальная переменная. Чаще всего (как в этих примерах) задачи классификации бывают двузначными, хотя встречаются и задачи с несколькими возможными состояниями.

В задачах регрессии требуется предсказать значение переменной, принимающей (как правило) непрерывные числовые значения: завтрашнюю цену акций, расход топлива в автомобиле, прибыли в следующем году и т.п.. В таких случаях в качестве выходной требуется одна числовая переменная.

Нейронная сеть может решать одновременно несколько задач регрессии и/или классификации, однако обычно в каждый момент решается только одна задача. Таким образом, в большинстве случаев нейронная сеть будет иметь всего одну выходную переменную; в случае задач классификации со многими состояниями для этого может потребоваться несколько выходных элементов (этап пост-процессирования отвечает за преобразование информации из выходных элементов в выходную переменную).



В пакете ST Neural Networks для решения всех этих вопросов реализованы специальные средства пре- и пост-процессирования, которые позволяют привести сырые исходные данные в числовую форму, пригодную для обработки нейронной сетью, и преобразовать выход нейронной сети обратно в формат входных данных. Нейронная сеть служит "прослойкой"между пре- и пост-процессированием, и результат выдается в нужном виде (например, в задаче классификации выдается название выходного класса). Кроме того, в пакете ST Neural Networks пользователь может (если пожелает) получить прямой доступ к внутренним параметрам активации сети.

В начало

Многослойный персептрон (MLP)
Многослойный персептрон (MLP)

Вероятно, эта архитектура сети используется сейчас наиболее часто. Она была предложена в работе Rumelhart, McClelland (1986) и подробно обсуждается почти во всех учебниках по нейронным сетям (см., например, Bishop, 1995). Вкратце этот тип сети был описан выше. Каждый элемент сети строит взвешенную сумму своих входов с поправкой в виде слагаемого и затем пропускает эту величину активации через передаточную функцию, и таким образом получается выходное значение этого элемента. Элементы организованы в послойную топологию с прямой передачей сигнала. Такую сеть легко можно интерпретировать как модель вход-выход, в которой веса и пороговые значения (смещения) являются свободными параметрами модели. Такая сеть может моделировать функцию практически любой степени сложности, причем число слоев и число элементов в каждом слое определяют сложность функции. Определение числа промежуточных слоев и числа элементов в них является важным вопросом при конструировании MLP (Haykin, 1994; Bishop, 1995). Количество входных и выходных элементов определяется условиями задачи. Сомнения могут возникнуть в отношении того, какие входные значения использовать, а какие нет, - к этому вопросу мы вернемся позже. Сейчас будем предполагать, что входные переменные выбраны интуитивно и что все они являются значимыми.


Вопрос же о том, сколько использовать промежуточных слоев и элементов в них, пока совершенно неясен. В качестве начального приближения можно взять один промежуточный слой, а число элементов в нем положить равным полусумме числа входных и выходных элементов. Опять-таки, позже мы обсудим этот вопрос подробнее.

Обучение многослойного персептрона
Обучение многослойного персептрона

После того, как определено число слоев и число элементов в каждом из них, нужно найти значения для весов и порогов сети, которые бы минимизировали ошибку прогноза, выдаваемого сетью. Именно для этого служат алгоритмы обучения. С использованием собранных исторических данных веса и пороговые значения автоматически корректируются с целью минимизировать эту ошибку. По сути этот процесс представляет собой подгонку модели, которая реализуется сетью, к имеющимся обучающим данным. Ошибка для конкретной конфигурации сети определяется путем прогона через сеть всех имеющихся наблюдений и сравнения реально выдаваемых выходных значений с желаемыми (целевыми) значениями. Все такие разности суммируются в так называемую функцию ошибок, значение которой и есть ошибка сети. В качестве функции ошибок чаще всего берется сумма квадратов ошибок, т.е. когда все ошибки выходных элементов для всех наблюдений возводятся в квадрат и затем суммируются. При работе с пакетом ST Neural Networks пользователю выдается так называемая среднеквадратичная ошибка (RMS) - описанная выше величина нормируется на число наблюдений и переменных, после чего из нее извлекается квадратный корень - это очень хорошая мера ошибки, усредненная по всему обучающему множеству и по всем выходным элементам.

В традиционном моделировании (например, линейном моделировании) можно алгоритмически определить конфигурацию модели, дающую абсолютный минимум для указанной ошибки. Цена, которую приходится платить за более широкие (нелинейные) возможности моделирования с помощью нейронных сетей, состоит в том, что, корректируя сеть с целью минимизировать ошибку, мы никогда не можем быть уверены, что нельзя добиться еще меньшей ошибки.



В этих рассмотрениях оказывается очень полезным понятие поверхности ошибок. Каждому из весов и порогов сети (т.е. свободных параметров модели; их общее число обозначим через N) соответствует одно измерение в многомерном пространстве. N+1-е измерение соответствует ошибке сети. Для всевозможных сочетаний весов соответствующую ошибку сети можно изобразить точкой в N+1-мерном пространстве, и все такие точки образуют там некоторую поверхность - поверхность ошибок. Цель обучения нейронной сети состоит в том, чтобы найти на этой многомерной поверхности самую низкую точку.

В случае линейной модели с суммой квадратов в качестве функции ошибок эта поверхность ошибок будет представлять собой параболоид (квадрику) - гладкую поверхность, похожую на часть поверхности сферы, с единственным минимумом. В такой ситуации локализовать этот минимум достаточно просто.

В случае нейронной сети поверхность ошибок имеет гораздо более сложное строение и обладает рядом неприятных свойств, в частности, может иметь локальные минимумы (точки, самые низкие в некоторой своей окрестности, но лежащие выше глобального минимума), плоские участки, седловые точки и длинные узкие овраги.

Аналитическими средствами невозможно определить положение глобального минимума на поверхности ошибок, поэтому обучение нейронной сети по сути дела заключается в исследовании поверхности ошибок. Отталкиваясь от случайной начальной конфигурации весов и порогов (т.е. случайно взятой точки на поверхности ошибок), алгоритм обучения постепенно отыскивает глобальный минимум. Как правило, для этого вычисляется градиент (наклон) поверхности ошибок в данной точке, а затем эта информация используется для продвижения вниз по склону. В конце концов алгоритм останавливается в нижней точке, которая может оказаться всего лишь локальным минимумом (а если повезет - глобальным минимумом).

Алгоритм обратного распространения
Алгоритм обратного распространения

Самый известный вариант алгоритма обучения нейронной сети - так называемый алгоритм обратного распространения (back propagation; см.


Patterson, 1996; Haykin, 1994; Fausett, 1994). Существуют современные алгоритмы второго порядка, такие как метод сопряженных градиентов и метод Левенберга-Маркара (Bishop, 1995; Shepherd, 1997) (оба они реализованы в пакете ST Neural Networks), которые на многих задачах работают существенно быстрее (иногда на порядок). Алгоритм обратного распространения наиболее прост для понимания, а в некоторых случаях он имеет определенные преимущества. Сейчас мы опишем его, а более продвинутые алгоритмы рассмотрим позже. Разработаны также эвристические модификации этого алгоритма, хорошо работающие для определенных классов задач, - быстрое распространение (Fahlman, 1988) и Дельта-дельта с чертой (Jacobs, 1988) - оба они также реализованы в пакете ST Neural Networks.

В алгоритме обратного распространения вычисляется вектор градиента поверхности ошибок. Этот вектор указывает направление кратчайшего спуска по поверхности из данной точки, поэтому если мы "немного" продвинемся по нему, ошибка уменьшится. Последовательность таких шагов (замедляющаяся по мере приближения к дну) в конце концов приведет к минимуму того или иного типа. Определенную трудность здесь представляет вопрос о том, какую нужно брать длину шагов.

При большой длине шага сходимость будет более быстрой, но имеется опасность перепрыгнуть через решение или (если поверхность ошибок имеет особо вычурную форму) уйти в неправильном направлении. Классическим примером такого явления при обучении нейронной сети является ситуация, когда алгоритм очень медленно продвигается по узкому оврагу с крутыми склонами, прыгая с одной его стороны на другую. Напротив, при маленьком шаге, вероятно, будет схвачено верное направление, однако при этом потребуется очень много итераций. На практике величина шага берется пропорциональной крутизне склона (так что алгоритм замедляет ход вблизи минимума) с некоторой константой, которая называется скоростью обучения. Правильный выбор скорости обучения зависит от конкретной задачи и обычно осуществляется опытным путем; эта константа может также зависеть от времени, уменьшаясь по мере продвижения алгоритма.



Обычно этот алгоритм видоизменяется таким образом, чтобы включать слагаемое импульса (или инерции). Этот член способствует продвижению в фиксированном направлении, поэтому если было сделано несколько шагов в одном и том же направлении, то алгоритм "увеличивает скорость", что (иногда) позволяет избежать локального минимума, а также быстрее проходить плоские участки.

Таким образом, алгоритм действует итеративно, и его шаги принято называть эпохами. На каждой эпохе на вход сети поочередно подаются все обучающие наблюдения, выходные значения сети сравниваются с целевыми значениями и вычисляется ошибка. Значение ошибки, а также градиента поверхности ошибок используется для корректировки весов, после чего все действия повторяются. Начальная конфигурация сети выбирается случайным образом, и процесс обучения прекращается либо когда пройдено определенное количество эпох, либо когда ошибка достигнет некоторого определенного уровня малости, либо когда ошибка перестанет уменьшаться (пользователь может сам выбрать нужное условие остановки).

Переобучение и обобщение
Переобучение и обобщение

Одна из наиболее серьезных трудностей изложенного подхода заключается в том, что таким образом мы минимизируем не ту ошибку, которую на самом деле нужно минимизировать, - ошибку, которую можно ожидать от сети, когда ей будут подаваться совершенно новые наблюдения. Иначе говоря, мы хотели бы, чтобы нейронная сеть обладала способностью обобщать результат на новые наблюдения. В действительности сеть обучается минимизировать ошибку на обучающем множестве, и в отсутствие идеального и бесконечно большого обучающего множества это совсем не то же самое, что минимизировать "настоящую" ошибку на поверхности ошибок в заранее неизвестной модели явления (Bishop, 1995).

Сильнее всего это различие проявляется в проблеме переобучения, или слишком близкой подгонки. Это явление проще будет продемонстрировать не для нейронной сети, а на примере аппроксимации посредством полиномов, - при этом суть явления абсолютно та же.



Полином (или многочлен) - это выражение, содержащее только константы и целые степени независимой переменной. Вот примеры:

y=2x+3
y=3x2+4x+1

Графики полиномов могут иметь различную форму, причем чем выше степень многочлена (и, тем самым, чем больше членов в него входит), тем более сложной может быть эта форма. Если у нас есть некоторые данные, мы можем поставить цель подогнать к ним полиномиальную кривую (модель) и получить таким образом объяснение для имеющейся зависимости. Наши данные могут быть зашумлены, поэтому нельзя считать, что самая лучшая модель задается кривой, которая в точности проходит через все имеющиеся точки. Полином низкого порядка может быть недостаточно гибким средством для аппроксимации данных, в то время как полином высокого порядка может оказаться чересчур гибким, и будет точно следовать данным, принимая при этом замысловатую форму, не имеющую никакого отношения к форме настоящей зависимости (см. Рисунок ).



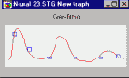
Нейронная сеть сталкивается с точно такой же трудностью. Сети с большим числом весов моделируют более сложные функции и, следовательно, склонны к переобучению. Сеть же с небольшим числом весов может оказаться недостаточно гибкой, чтобы смоделировать имеющуюся зависимость. Например, сеть без промежуточных слоев на самом деле моделирует обычную линейную функцию.

Как же выбрать "правильную" степень сложности для сети? Почти всегда более сложная сеть дает меньшую ошибку, но это может свидетельствовать не о хорошем качестве модели, а о переобучении.

Ответ состоит в том, чтобы использовать механизм контрольной кросс-проверки. Мы резервируем часть обучающих наблюдений и не используем их в обучении по алгоритму обратного распространения. Вместо этого, по мере работы алгоритма, они используются для независимого контроля результата. В самом начале работы ошибка сети на обучающем и контрольном множестве будет одинаковой (если они существенно отличаются, то, вероятно, разбиение всех наблюдений на два множества было неоднородно). По мере того, как сеть обучается, ошибка обучения, естественно, убывает, и, пока обучение уменьшает действительную функцию ошибок, ошибка на контрольном множестве также будет убывать.


Если же контрольная ошибка перестала убывать или даже стала расти, это указывает на то, что сеть начала слишком близко аппроксимировать данные и обучение следует остановить (в пакете ST Neural Networks можно задать автоматическую остановку обучения при появлении эффекта переобучения). Это явление чересчур точной аппроксимации в процессе обучения и называется переобучением. Если такое случилось, то обычно советуют уменьшить число скрытых элементов и/или слоев, ибо сеть является слишком мощной для данной задачи. Если же сеть, наоборот, была взята недостаточно богатой для того, чтобы моделировать имеющуюся зависимость, то переобучения, скорее всего, не произойдет, и обе ошибки - обучения и проверки - не достигнут достаточного уровня малости.

Описанные проблемы с локальными минимумами и выбором размера сети приводят к тому, что при практической работе с нейронными сетями, как правило, приходится экспериментировать с большим числом различных сетей, порой обучая каждую из них по нескольку раз (чтобы не быть введенным в заблуждение локальными минимумами) и сравнивая полученные результаты. Главным показателем качества результата является здесь контрольная ошибка. При этом, в соответствии с общенаучным принципом, согласно которому при прочих равных следует предпочесть более простую модель, из двух сетей с приблизительно равными ошибками контроля имеет смысл выбрать ту, которая меньше.

Необходимость многократных экспериментов ведет к тому, что контрольное множество начинает играть ключевую роль в выборе модели, то есть становится частью процесса обучения. Тем самым ослабляется его роль как независимого критерия качества модели - при большом числе экспериментов есть риск выбрать "удачную" сеть, дающую хороший результат на контрольном множестве. Для того, чтобы придать окончательной модели должную надежность, часто (по крайней мере, когда объем обучающих данных это позволяет) поступают так: резервируют еще одно - тестовое множество наблюдений. Итоговая модель тестируется на данных из этого множества, чтобы убедиться, что результаты, достигнутые на обучающем и контрольном множествах реальны, а не являются артефактами процесса обучения.


Разумеется, для того чтобы хорошо играть свою роль, тестовое множество должно быть использовано только один раз: если его использовать повторно для корректировки процесса обучения, то оно фактически превратится в контрольное множество.

Итак, построение сети (после выбора входных переменных) состоит из следующих шагов: Выбрать начальную конфигурацию сети (например, один промежуточный слой с числом элементов в нем, равным полусумме числа входов и числа выходов - Наставник (Network Advisor) пакета ST Neural Networks предложит Вам такую конфигурацию по умолчанию). Провести ряд экспериментов с различными конфигурациями, запоминая при этом лучшую сеть (в смысле контрольной ошибки). В пакете ST Neural Networks предусмотрено автоматическое запоминание лучшей сети во время эксперимента. Для каждой конфигурации следует провести несколько экспериментов, чтобы не получить ошибочный результат из-за того, что процесс обучения попал в локальный минимум. Если в очередном эксперименте наблюдается недообучение (сеть не выдает результат приемлемого качества), попробовать добавить дополнительные нейроны в промежуточный слой (слои). Если это не помогает, попробовать добавить новый промежуточный слой. Если имеет место переобучение (контрольная ошибка стала расти), попробовать удалить несколько скрытых элементов (а возможно и слоев). Многократное повторение эвристических экспериментов в лучшем случае довольно утомительно, и поэтому в пакет ST Neural Networks включен специальный алгоритм автоматического поиска, который проделает эти действия за Вас. Автоматический конструктор сети - Automatic Network Designer проведет эксперименты с различным числом скрытых элементов, для каждой пробной архитектуры сети выполнит несколько прогонов обучения, отбирая при этом наилучшую сеть по показателю контрольной ошибки с поправкой на размер сети. В Автоматическом конструкторе сети реализованы сложные алгоритмы поиска, в том числе метод "искусственного отжига" (simulated annealing, Kirkpatrick et al., 1983), с помощью которых можно перепробовать сотни различных сетей, выделяя из них особо перспективные, либо быстро находить "грубое и простое" решение.



Отбор данных
Отбор данных

На всех предыдущих этапах существенно использовалось одно предположение. А именно, обучающее, контрольное и тестовое множества должны быть репрезентативными (представительными) с точки зрения существа задачи (более того, эти множества должны быть репрезентативными каждое в отдельности). Известное изречение программистов "garbage in, garbage out" ("мусор на входе - мусор на выходе") нигде не справедливо в такой степени, как при нейросетевом моделировании. Если обучающие данные не репрезентативны, то модель, как минимум, будет не очень хорошей, а в худшем случае - бесполезной. Имеет смысл перечислить ряд причин, которые ухудшают качество обучающего множества:

Будущее непохоже на прошлое. Обычно в качестве обучающих берутся исторические данные. Если обстоятельства изменились, то закономерности, имевшие место в прошлом, могут больше не действовать.

Следует учесть все возможности.
Следует учесть все возможности.

Нейронная сеть может обучаться только на тех данных, которыми она располагает. Предположим, что лица с годовым доходом более $100,000 имеют высокий кредитный риск, а обучающее множество не содержало лиц с доходом более $40,000 в год. Тогда едва ли можно ожидать от сети правильного решения в совершенно новой для нее ситуации.

Сеть обучается тому, чему проще всего обучиться. Классическим (возможно, вымышленным) примером является система машинного зрения, предназначенная для автоматического распознавания танков. Сеть обучалась на ста картинках, содержащих изображения танков, и на ста других картинках, где танков не было. Был достигнут стопроцентно "правильный" результат. Но когда на вход сети были поданы новые данные, она безнадежно провалилась. В чем же была причина? Выяснилось, что фотографии с танками были сделаны в пасмурный, дождливый день, а фотографии без танков - в солнечный день. Сеть научилась улавливать (очевидную) разницу в общей освещенности. Чтобы сеть могла результативно работать, ее следовало обучать на данных, где бы присутствовали все погодные условия и типы освещения, при которых сеть предполагается использовать - и это еще не говоря о рельефе местности, угле и дистанции съемки и т.д.



Несбалансированный набор данных.
Несбалансированный набор данных.

Коль скоро сеть минимизирует общую погрешность, важное значение приобретает пропорции, в которых представлены данные различных типов. Сеть, обученная на 900 хороших и 100 плохих примерах будет искажать результат в пользу хороших наблюдений, поскольку это позволит алгоритму уменьшить общую погрешность (которая определяется в основном хорошими случаями). Если в реальной популяции хорошие и плохие объекты представлены в другой пропорции, то результаты, выдаваемые сетью, могут оказаться неверными. Хорошим примером служит задача выявления заболеваний. Пусть, например, при обычных обследованиях в среднем 90% людей оказываются здоровыми. Сеть обучается на имеющихся данных, в которых пропорция здоровые/больные равна 90/10. Затем она применяется для диагностики пациентов с определенным жалобами, среди которых это соотношение уже 50/50. В этом случае сеть будет ставить диагноз чересчур осторожно и не распознает заболевание у некоторых больных. Если же, наоборот, сеть обучить на данных "с жалобами", а затем протестировать на "обычных" данных, то она будет выдавать повышенное число неправильных диагнозов о наличии заболевания. В таких ситуациях обучающие данные нужно скорректировать так, чтобы были учтены различия в распределении данных (например, можно повторять редкие наблюдения или удалить часто встречающиеся), или же видоизменить решения, выдаваемые сетью, посредством матрицы потерь (Bishop, 1995). Как правило, лучше всего постараться сделать так, чтобы наблюдения различных типов были представлены равномерно, и соответственно этому интерпретировать результаты, которые выдает сеть.

Как обучается многослойный персептрон
Как обучается многослойный персептрон

Мы сможем лучше понять, как устроен и как обучается многослойный персептрон (MLP), если выясним, какие функции он способен моделировать. Вспомним, что уровнем активации элемента называется взвешенная сумма его входов с добавленным к ней пороговым значением.


Таким образом, уровень активации представляет собой простую линейную функцию входов. Эта активация затем преобразуется с помощью сигмоидной ( имеющей S-образную форму) кривой.



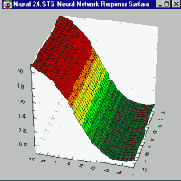
Комбинация линейной функции нескольких переменных и скалярной сигмоидной функции приводит к характерному профилю "сигмоидного склона", который выдает элемент первого промежуточного слоя MLP (На приведенном здесь рисунке соответствующая поверхность изображена в виде функции двух входных переменных. Элемент с большим числом входов выдает многомерный аналог такой поверхности). При изменении весов и порогов меняется и поверхность отклика. При этом может меняться как ориентация всей поверхности, так и крутизна склона. Большим значениям весов соответствует более крутой склон. Так например, если увеличить все веса в два раза, то ориентация не изменится, а наклон будет более крутым.



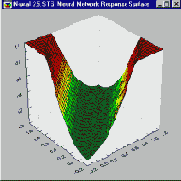
В многослойной сети подобные функции отклика комбинируются друг с другом с помощью последовательного взятия их линейных комбинаций и применения нелинейных функций активации. На этом рисунке изображена типичная поверхность отклика для сети с одним промежуточным слоем, состоящим из двух элементов, и одним выходным элементом, для классической задачи "исключающего или" (Xor). Две разных сигмоидных поверхности объединены в одну поверхность, имеющую форму буквы "U".

Перед началом обучения сети весам и порогам случайным образом присваиваются небольшие по величине начальные значения. Тем самым отклики отдельных элементов сети имеют малый наклон и ориентированы хаотично - фактически они не связаны друг с другом. По мере того, как происходит обучение, поверхности отклика элементов сети вращаются и сдвигаются в нужное положение, а значения весов увеличиваются, поскольку они должны моделировать отдельные участки целевой поверхности отклика.

В задачах классификации выходной элемент должен выдавать сильный сигнал в случае, если данное наблюдение принадлежит к интересующему нас классу, и слабый - в противоположном случае.


Иначе говоря, этот элемент должен стремиться смоделировать функцию, равную единице в той области пространства объектов, где располагаются объекты из нужного класса, и равную нулю вне этой области. Такая конструкция известна как дискриминантная функция в задачах распознавания. "Идеальная" дискриминантная функция должна иметь плоскую структуру, так чтобы точки соответствующей поверхности располагались либо на нулевом уровне, либо на высоте единица.

Если сеть не содержит скрытых элементов, то на выходе она может моделировать только одинарный "сигмоидный склон": точки, находящиеся по одну его сторону, располагаются низко, по другую - высоко. При этом всегда будет существовать область между ними (на склоне), где высота принимает промежуточные значения, но по мере увеличения весов эта область будет сужаться.

Такой сигмоидный склон фактически работает как линейная дискриминантная функция. Точки, лежащие по одну сторону склона, классифицируются как принадлежащие нужному классу, а лежащие по другую сторону - как не принадлежащие. Следовательно, сеть без скрытых слоев может служить классификатором только в линейно-отделимых задачах (когда можно провести линию - или, в случае более высоких размерностей, - гиперплоскость, разделяющую точки в пространстве признаков).

Сеть, содержащая один промежуточный слой, строит несколько сигмоидных склонов - по одному для каждого скрытого элемента, - и затем выходной элемент комбинирует из них "возвышенность". Эта возвышенность получается выпуклой, т.е. не содержащей впадин. При этом в некоторых направлениях она может уходить на бесконечность (как длинный полуостров). Такая сеть может моделировать большинство реальных задач классификации.



На этом рисунке показана поверхность отклика, полученная многослойным персептроном для решения задачи исключающего или: хорошо видно, что она выделяет область пространства, расположенную вдоль диагонали.

Сеть с двумя промежуточными слоями строит комбинацию из нескольких таких возвышенностей.


Их будет столько же, сколько элементов во втором слое, и у каждой из них будет столько сторон, сколько элементов было в первом скрытом слое. После небольшого размышления можно прийти к выводу, что, используя достаточное число таких возвышенностей, можно воспроизвести поверхность любой формы - в том числе с впадинами и вогнутостями.

Как следствие наших рассмотрений мы получаем, что, теоретически, для моделирования любой задачи достаточно многослойного персептрона с двумя промежуточными слоями (в точной формулировке этот результат известен как теорема Колмогорова). При этом может оказаться и так, что для решения некоторой конкретной задачи более простой и удобной будет сеть с еще большим числом слоев. Однако, для решения большинства практических задач достаточно всего одного промежуточного слоя, два слоя применяются как резерв в особых случаях, а сети с тремя слоями практически не применяются.

В задачах классификации очень важно понять, как следует интерпретировать те точки, которые попали на склон или лежат близко от него. Стандартный выход здесь состоит в том, чтобы для пороговых значений установить некоторые доверительные пределы (принятия или отвержения), которые должны быть достигнуты, чтобы данных элемент считался "принявшим решение". Например, если установлены пороги принятия/отвержения 0.95/0.05, то при уровне выходного сигнала, превосходящем 0.95 элемент считается активным, при уровне ниже 0.05 - неактивным, а в промежутке - "неопределенным".

Имеется и более тонкий (и, вероятно, более полезный) способ интерпретировать уровни выходного сигнала: считать их вероятностями. В этом случае сеть выдает несколько большую информацию, чем просто "да/нет": она сообщает нам, насколько (в некотором формальном смысле) мы можем доверять ее решению. Разработаны (и реализованы в пакете ST Neural Networks) модификации метода MLP, позволяющие интерпретировать выходной сигнал нейронной сети как вероятность, в результате чего сеть по существу учится моделировать плотность вероятности распределения данного класса.


При этом, однако, вероятностная интерпретация обоснована только в том случае, если выполнены определенные предположения относительно распределения исходных данных (конкретно, что они являются выборкой из некоторого распределения, принадлежащего к семейству экспоненциальных распределений; Bishop, 1995). Здесь, как и ранее, может быть принято решение по классификации, но, кроме того, вероятностная интерпретация позволяет ввести концепцию "решения с минимальными затратами".

Другие алгоритмы обучения MLP
Другие алгоритмы обучения MLP

Выше было описано, как с помощью алгоритма обратного распространения осуществляется градиентный спуск по поверхности ошибок. Вкратце дело происходит так: в данной точке поверхности находится направление скорейшего спуска, затем делается прыжок вниз на расстояние, пропорциональное коэффициенту скорости обучения и крутизне склона, при этом учитывается инерция, те есть стремление сохранить прежнее направление движения. Можно сказать, что метод ведет себя как слепой кенгуру - каждый раз прыгает в направлении, которое кажется ему наилучшим. На самом деле шаг спуска вычисляется отдельно для всех обучающих наблюдений, взятых в случайном порядке, но в результате получается достаточно хорошая аппроксимация спуска по совокупной поверхности ошибок. Существуют и другие алгоритмы обучения MLP, однако все они используют ту или иную стратегию скорейшего продвижения к точке минимума.

В некоторых задачах бывает целесообразно использовать такие - более сложные - методы нелинейной оптимизации. В пакете ST Neural Networks реализованы два подобных метода: методы спуска по сопряженным градиентам и Левенберга -Маркара (Bishop, 1995; Shepherd, 1997), представляющие собой очень удачные варианты реализации двух типов алгоритмов: линейного поиска и доверительных областей.

Алгоритм линейного поиска действует следующим образом: выбирается какое-либо разумное направление движения по многомерной поверхности. В этом направлении проводится линия, и на ней ищется точка минимума (это делается относительно просто с помощью того или иного варианта метода деления отрезка пополам); затем все повторяется сначала.


Что в данном случае следует считать "разумным направлением"? Очевидным ответом является направление скорейшего спуска (именно так действует алгоритм обратного распространения). На самом деле этот вроде бы очевидный выбор не слишком удачен. После того, как был найден минимум по некоторой прямой, следующая линия, выбранная для кратчайшего спуска, может "испортить" результаты минимизации по предыдущему направлению (даже на такой простой поверхности, как параболоид, может потребоваться очень большое число шагов линейного поиска). Более разумно было бы выбирать "не мешающие друг другу " направления спуска - так мы приходим к методу сопряженных градиентов (Bishop, 1995).

Идея метода состоит в следующем: поскольку мы нашли точку минимума вдоль некоторой прямой, производная по этому направлению равна нулю. Сопряженное направление выбирается таким образом, чтобы эта производная и дальше оставалась нулевой - в предположении, что поверхность имеет форму параболоида (или, грубо говоря, является "хорошей и гладкой "). Если это условие выполнено, то для достижения точки минимума достаточно будет N эпох. На реальных, сложно устроенных поверхностях по мере хода алгоритма условие сопряженности портится, и тем не менее такой алгоритм, как правило, требует гораздо меньшего числа шагов, чем метод обратного распространения, и дает лучшую точку минимума (для того, чтобы алгоритм обратного распространения точно установился в некоторой точке, нужно выбирать очень маленькую скорость обучения).

Метод доверительных областей основан на следующей идее: вместо того, чтобы двигаться в определенном направлении поиска, предположим, что поверхность имеет достаточно простую форму, так что точку минимума можно найти (и прыгнуть туда) непосредственно. Попробуем смоделировать это и посмотреть, насколько хорошей окажется полученная точка. Вид модели предполагает, что поверхность имеет хорошую и гладкую форму (например, является параболоидом), - такое предположение выполнено вблизи точек минимума.


Вдали от них данное предположение может сильно нарушаться, так что модель будет выбирать для очередного продвижения совершенно не те точки. Правильно работать такая модель будет только в некоторой окрестности данной точки, причем размеры этой окрестности заранее неизвестны. Поэтому выберем в качестве следующей точки для продвижения нечто промежуточное между точкой, которую предлагает наша модель, и точкой, которая получилась бы по обычному методу градиентного спуска. Если эта новая точка оказалась хорошей, передвинемся в нее и усилим роль нашей модели в выборе очередных точек; если же точка оказалась плохой, не будем в нее перемещаться и увеличим роль метода градиентного спуска при выборе очередной точки (а также уменьшим шаг). В основанном на этой идее методе Левенберга-Маркара предполагается, что исходное отображение является локально линейным (и тогда поверхность ошибок будет параболоидом).

Метод Левенберга-Маркара (Levenberg, 1944; Marquardt, 1963; Bishop, 1995) - самый быстрый алгоритм обучения из всех, которые реализованы в пакете ST Neural Networks, но, к сожалению, на его использование имеется ряд важных ограничений. Он применим только для сетей с одним выходным элементом, работает только с функцией ошибок сумма квадратов и требует памяти порядка W**2 (где W - количество весов у сети; поэтому для больших сетей он плохо применим). Метод сопряженных градиентов почти так же эффективен, как и этот метод, и не связан подобными ограничениями.

При всем сказанном метод обратного распространения также сохраняет свое значение, причем не только для тех случаев, когда требуется быстро найти решение (и не требуется особой точности). Его следует предпочесть, когда объем данных очень велик, и среди данных есть избыточные. Благодаря тому, что в методе обратного распространения корректировка ошибки происходит по отдельным случаям, избыточность данных не вредит (если, например, приписать к имеющемуся набору данных еще один точно такой же набор, так что каждый случай будет повторяться дважды, то эпоха будет занимать вдвое больше времени, чем раньше, однако результат ее будет точно таким же, как от двух старых, так что ничего плохого не произойдет).


Методы же Левенберга-Маркара и сопряженных градиентов проводят вычисления на всем наборе данных, поэтому при увеличении числа наблюдений продолжительность одной эпохи сильно растет, но при этом совсем не обязательно улучшается результат, достигнутый на этой эпохе (в частности, если данные избыточны; если же данные редкие, то добавление новых данных улучшит обучение на каждой эпохе). Кроме того, обратное распространение не уступает другим методам в ситуациях, когда данных мало, поскольку в этом случае недостаточно данных для принятия очень точного решения (более тонкий алгоритм может дать меньшую ошибку обучения, но контрольная ошибка у него, скорее всего, не будет меньше).

Кроме уже перечисленных, в пакете ST Neural Networks имеются две модификации метода обратного распространения - метод быстрого распространения (Fahlman, 1988) и дельта-дельта с чертой (Jacobs, 1988), - разработанные с целью преодолеть некоторые ограничения этого подхода. В большинстве случаев они работают не лучше, чем обратное распространение, а иногда и хуже (это зависит от задачи). Кроме того, в этих методах используется больше управляющих параметров, чем в других методах, и поэтому ими сложнее пользоваться. Мы не будем описывать это методы подробно в данной главе.

В начало

Радиальная базисная функция
Радиальная базисная функция

В предыдущем разделе было описано, как многослойный персептрон моделирует функцию отклика с помощью функций "сигмоидных склонов " - в задачах классификации это соответствует разбиению пространства входных данных посредством гиперплоскостей. Метод разбиения пространства гиперплоскостями представляется естественным и интуитивно понятным, ибо он использует фундаментальное простое понятие прямой линии. Столь же естественным является подход, основанный на разбиении пространства окружностями или (в общем случае) гиперсферами. Гиперсфера задается своим центром и радиусом. Подобно тому, как элемент MLP реагирует (нелинейно) на расстояние от данной точки до линии "сигмоидного склона", в сети, построенной на радиальных базисных функциях (Broomhead and Lowe, 1988; Moody and Darkin, 1989; Haykin, 1994), элемент реагирует (нелинейно) на расстояние от данной точки до "центра", соответствующего этому радиальному элементу.


Поверхность отклика радиального элемента представляет собой гауссову функцию (колоколообразной формы), с вершиной в центре и понижением к краям. Наклон гауссова радиального элемента можно менять подобно тому, как можно менять наклон сигмоидной кривой в MLP (см. Рисунок ).



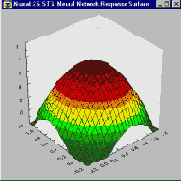
Элемент многослойного персептрона полностью задается значениями своих весов и порогов, которые в совокупности определяют уравнение разделяющей прямой и скорость изменения функции при отходе от этой линии. До действия сигмоидной функции активации уровень активации такого элемента определяется гиперплоскостью, поэтому в системе ST Neural Networks такие элементы называется линейными (хотя функция активации, как правило, нелинейна). В отличие от них, радиальный элемент задается своим центром и "радиусом". Положение точки в N-мерном пространстве определяется N числовыми параметрами, т.е. их ровно столько же, сколько весов у линейного элемента, и поэтому координаты центра радиального элемента в пакете ST Neural Networks хранятся как "веса". Его радиус (отклонение) хранится как "порог". Следует отчетливо понимать, что "веса" и "пороги" радиального элемента принципиально отличаются от весов и порогов линейного элемента, и если забыть об этом, термин может ввести Вас в заблуждение. Радиальные веса на самом деле представляют точку, а радиальный порог - отклонение.

Сеть типа радиальной базисной функции (RBF) имеет промежуточный слой из радиальных элементов, каждый из которых воспроизводит гауссову поверхность отклика. Поскольку эти функции нелинейны, для моделирования произвольной функции нет необходимости брать более одного промежуточного слоя. Для моделирования любой функции необходимо лишь взять достаточное число радиальных элементов. Остается решить вопрос о том, как следует скомбинировать выходы скрытых радиальных элементов, чтобы получить из них выход сети. Оказывается, что достаточно взять их линейную комбинацию (т.е. взвешенную сумму гауссовых функций).


Сеть RBF имеет выходной слой, состоящий из элементов с линейными функциями активации (Haykin, 1994; Bishop, 1995).

Сети RBF имеют ряд преимуществ перед сетями MLP. Во-первых, как уже сказано, они моделируют произвольную нелинейную функцию с помощью всего одного промежуточного слоя, и тем самым избавляют нас от необходимости решать вопрос о числе слоев. Во-вторых, параметры линейной комбинации в выходном слое можно полностью оптимизировать с помощью хорошо известных методов линейного моделирования, которые работают быстро и не испытывают трудностей с локальными минимумами, так мешающими при обучении MLP. Поэтому сеть RBF обучается очень быстро (на порядок быстрее MLP).

С другой стороны, до того, как применять линейную оптимизацию в выходном слое сети RBF, необходимо определить число радиальных элементов, положение их центров и величины отклонений. Соответствующие алгоритмы, хотя и работают быстрее алгоритмов обучения MLP, в меньшей степени пригодны для отыскания субоптимальных решений. В качестве компенсации, Автоматический конструктор сети пакета ST Neural Networks сможет выполнить за Вас все необходимые действия по экспериментированию с сетью.

Другие отличия работы RBF от MLP связаны с различным представлением пространства модели: "групповым" в RBF и "плоскостным" в MLP.

Опыт показывает, что для правильного моделирования типичной функции сеть RBF, с ее более эксцентричной поверхностью отклика, требует несколько большего числа элементов. Конечно, можно специально придумать форму поверхности, которая будет хорошо представляться первым или, наоборот, вторым способом, но общий итог оказывается не в пользу RBF. Следовательно, модель, основанная на RBF, будет работать медленнее и потребует больше памяти, чем соответствующий MLP (однако она гораздо быстрее обучается, а в некоторых случаях это важнее).

С "групповым" подходом связано и неумение сетей RBF экстраполировать свои выводы за область известных данных. При удалении от обучающего множества значение функции отклика быстро спадает до нуля.


Напротив, сеть MLP выдает более определенные решения при обработке сильно отклоняющихся данных. Достоинство это или недостаток - зависит от конкретной задачи, однако в целом склонность MLP к некритическому экстраполированию результата считается его слабостью. Экстраполяция на данные, лежащие далеко от обучающего множества, - вещь, как правило, опасная и необоснованная.

Сети RBF более чувствительны к "проклятию размерности" и испытывают значительные трудности, когда число входов велико. Мы обсудим этот вопрос ниже.

Как уже говорилось, обучение RBF-сети происходит в несколько этапов. Сначала определяются центры и отклонения для радиальных элементов; после этого оптимизируются параметры линейного выходного слоя.

Расположение центров должно соответствовать кластерам, реально присутствующим в исходных данных. Рассмотрим два наиболее часто используемых метода.

Расположение центров должно соответствовать кластерам, реально присутствующим в исходных данных. Рассмотрим два наиболее часто изпользуемых метода.

Выборка из выборки. В качестве центров радиальных элементов берутся несколько случайно выбранных точек обучающего множества. В силу случайности выбора они "представляют" распределение обучающих данных в статистическом смысле. Однако, если число радиальных элементов невелико, такое представление может быть неудовлетворительным (Haykin, 1994).

Алгоритм K-средних.
Алгоритм K-средних.

Этот алгоритм (Bishop, 1995) стремится выбрать оптимальное множество точек, являющихся центроидами кластеров в обучающих данных. При K радиальных элементах их центры располагаются таким образом, чтобы: Каждая обучающая точка "относилась" к одному центру кластера и лежала к нему ближе, чем к любому другому центру; Каждый центр кластера был центроидом множества обучающих точек, относящихся к этому кластеру. После того, как определено расположение центров, нужно найти отклонения. Величина отклонения (ее также называют сглаживающим фактором) определяет, насколько "острой" будет гауссова функция.


Если эти функции выбраны слишком острыми, сеть не будет интерполировать данные между известными точками и потеряет способность к обобщению. Если же гауссовы функции взяты чересчур широкими, сеть не будет воспринимать мелкие детали. На самом деле сказанное - еще одна форма проявления дилеммы пере/недообучения. Как правило, отклонения выбираются таким образом, чтобы колпак каждой гауссовой функций захватывал "несколько" соседних центров. Для этого имеется несколько методов:

Явный. Отклонения задаются пользователем.

Изотропный. Отклонение берется одинаковым для всех элементов и определяется эвристически с учетом количества радиальных элементов и объема покрываемого пространства (Haykin, 1994).

K ближайших соседей. Отклонение каждого элемента устанавливается (индивидуально) равным среднему расстоянию до его K ближайших соседей (Bishop, 1995). Тем самым отклонения будут меньше в тех частях пространства, где точки расположены густо, - здесь будут хорошо учитываться детали, - а там, где точек мало, отклонения будут большими (и будет производится интерполяция).

После того, как выбраны центры и отклонения, параметры выходного слоя оптимизируются с помощью стандартного метода линейной оптимизации - алгоритма псевдообратных матриц (сингулярного разложения) (Haykin, 1994; Golub and Kahan, 1965).

Могут быть построены различные гибридные разновидности радиальных базисных функций. Например, выходной слой может иметь нелинейные функции активации, и тогда для его обучения используется какой-либо из алгоритмов обучения многослойных персептронов, например метод обратного распространения. Можно также обучать радиальный (скрытый) слой с помощью алгоритма обучения сети Кохонена - это еще один способ разместить центры так, чтобы они отражали расположение данных.

В начало

Вероятностная нейронная сеть
Вероятностная нейронная сеть

В предыдущем разделе, говоря о задачах классификации, мы кратко упомянули о том, что выходы сети можно с пользой интерпретировать как оценки вероятности того, что элемент принадлежит некоторому классу, и сеть фактически учится оценивать функцию плотности вероятности.


Аналогичная полезная интерпретация может иметь место и в задачах регрессии - выход сети рассматривается как ожидаемое значение модели в данной точке пространства входов. Это ожидаемое значение связано с плотностью вероятности совместного распределения входных и выходных данных. Задача оценки плотности вероятности (p.d.f.) по данным имеет давнюю историю в математической статистике (Parzen, 1962) и относится к области байесовой статистики. Обычная статистика по заданной модели говорит нам, какова будет вероятность того или иного исхода (например, что на игральной кости шесть очков будет выпадать в среднем одном случае из шести). Байесова статистика переворачивает вопрос вверх ногами: правильность модели оценивается по имеющимся достоверным данным. В более общем плане, байесова статистика дает возможность оценивать плотность вероятности распределений параметров модели по имеющимся данных. Для того, чтобы минимизировать ошибку, выбирается модель с такими параметрами, при которых плотность вероятности будет наибольшей.

При решении задачи классификации можно оценить плотность вероятности для каждого класса, сравнить между собой вероятности принадлежности различным классам и выбрать наиболее вероятный. На самом деле именно это происходит, когда мы обучаем нейронную сеть решать задачу классификации - сеть пытается определить (т.е. аппроксимировать) плотность вероятности.

Традиционный подход к задаче состоит в том, чтобы построить оценку для плотности вероятности по имеющимся данным. Обычно при этом предполагается, что плотность имеет некоторый определенный вид (чаще всего - что она имеет нормальное распределение). После этого оцениваются параметры модели. Нормальное распределение часто используется потому, что тогда параметры модели (среднее и стандартное отклонение) можно оценить аналитически. При этом остается вопрос о том, что предположение о нормальности не всегда оправдано.

Другой подход к оценке плотности вероятности основан на ядерных оценках (Parzen, 1962; Speckt, 1990; Speckt, 1991; Bishop, 1995; Patterson, 1996).


Можно рассуждать так: тот факт, что наблюдение расположено в данной точке пространства, свидетельствует о том, что в этой точке имеется некоторая плотность вероятности. Кластеры из близко лежащих точек указывают на то, что в этом месте плотность вероятности большая. Вблизи наблюдения имеется большее доверие к уровню плотности, а по мере отдаления от него доверие убывает и стремится к нулю. В методе ядерных оценок в точке, соответствующей каждому наблюдению, помещается некоторая простая функция, затем все они складываются и в результате получается оценка для общей плотности вероятности. Чаще всего в качестве ядерных функций берутся гауссовы функции (с формой колокола). Если обучающих примеров достаточное количество, то такой метод дает достаточно хорошее приближение к истинной плотности вероятности.

Метод аппроксимации плотности вероятности с помощью ядерных функций во многом похож на метод радиальных базисных функций, и таким образом мы естественно приходим к понятиям вероятностной нейронной сети (PNN) и обобщенно-регрессионной нейронной сети (GRNN) (Speckt 1990, 1991). PNN-сети предназначены для задач классификации, а GRNN - для задач регрессии. Сети этих двух типов представляют собой реализацию методов ядерной аппроксимации, оформленных в виде нейронной сети.

Сеть PNN имеет по меньшей мере три слоя: входной, радиальный и выходной. Радиальные элементы берутся по одному на каждое обучающее наблюдение. Каждый из них представляет гауссову функцию с центром в этом наблюдении. Каждому классу соответствует один выходной элемент. Каждый такой элемент соединен со всеми радиальными элементами, относящимися к его классу, а со всеми остальными радиальными элементами он имеет нулевое соединение. Таким образом, выходной элемент просто складывает отклики всех элементов, принадлежащих к его классу. Значения выходных сигналов получаются пропорциональными ядерным оценкам вероятности принадлежности соответствующим классам, и пронормировав их на единицу, мы получаем окончательные оценки вероятности принадлежности классам.



Базовая модель PNN-сети может иметь две модификации.

В первом случае мы предполагаем, что пропорции классов в обучающем множестве соответствуют их пропорциям во всей исследуемой популяции (или так называемым априорным вероятностям). Например, если среди всех людей больными являются 2%, то в обучающем множестве для сети, диагностирующей заболевание, больных должно быть тоже 2%. Если же априорные вероятности будут отличаться от пропорций в обучающей выборке, то сеть будет выдавать неправильный результат. Это можно впоследствии учесть (если стали известны априорные вероятности), вводя поправочные коэффициенты для различных классов.

Второй вариант модификации основан на следующей идее. Любая оценка, выдаваемая сетью, основывается на зашумленных данных и неизбежно будет приводить к отдельным ошибкам классификации (например, у некоторых больных результаты анализов могут быть вполне нормальными). Иногда бывает целесообразно считать, что некоторые виды ошибок обходятся "дороже" других (например, если здоровый человек будет диагностирован как больной, то это вызовет лишние затраты на его обследование, но не создаст угрозы для жизни; если же не будет выявлен действительный больной, то это может привести к смертельному исходу). В такой ситуации те вероятности, которые выдает сеть, следует домножить на коэффициенты потерь, отражающие относительную цену ошибок классификации. В пакете ST Neural Networks в вероятностную нейронную сеть может быть добавлен четвертый слой, содержащий матрицу потерь. Она умножается на вектор оценок, полученный в третьем слое, после чего в качестве ответа берется класс, имеющий наименьшую оценку потерь. (Матрицу потерь можно добавлять и к другим видам сетей, решающих задачи классификации.)

Вероятностная нейронная сеть имеет единственный управляющий параметр обучения, значение которого должно выбираться пользователем, - степень сглаживания (или отклонение гауссовой функции). Как и в случае RBF-сетей, этот параметр выбирается из тех соображений, чтобы шапки " определенное число раз перекрывались": выбор слишком маленьких отклонений приведет к "острым" аппроксимирующим функциям и неспособности сети к обобщению, а при слишком больших отклонениях будут теряться детали.


Требуемое значение несложно найти опытным путем, подбирая его так, чтобы контрольная ошибка была как можно меньше. К счастью, PNN-сети не очень чувствительны к выбору параметра сглаживания.

Наиболее важные преимущества PNN-сетей состоят в том, что выходное значение имеет вероятностный смысл (и поэтому его легче интерпретировать), и в том, что сеть быстро обучается. При обучения такой сети время тратится практически только на то, чтобы подавать ей на вход обучающие наблюдения, и сеть работает настолько быстро, насколько это вообще возможно.

Существенным недостатком таких сетей является их объем. PNN-сеть фактически вмещает в себя все обучающие данные, поэтому она требует много памяти и может медленно работать.

PNN-сети особенно полезны при пробных экспериментах (например, когда нужно решить, какие из входных переменных использовать), так как благодаря короткому времени обучения можно быстро проделать большое количество пробных тестов. В пакете ST Neural Networks PNN-сети используются также в Нейро-генетическом алгоритме отбора входных данных - Neuro-Genetic Input Selection, который автоматически находит значимые входы (будет описан ниже).

В начало

Обобщенно-регрессионная нейронная сеть
Обобщенно-регрессионная нейронная сеть

Обобщенно-регрессионная нейронная сеть (GRNN) устроена аналогично вероятностной нейронной сети (PNN), но она предназначена для решения задач регрессии, а не классификации (Speckt, 1991; Patterson, 1996; Bishop, 1995). Как и в случае PNN-сети, в точку расположения каждого обучающего наблюдения помещается гауссова ядерная функция. Мы считаем, что каждое наблюдение свидетельствует о некоторой нашей уверенности в том, что поверхность отклика в данной точке имеет определенную высоту, и эта уверенность убывает при отходе в сторону от точки. GRNN-сеть копирует внутрь себя все обучающие наблюдения и использует их для оценки отклика в произвольной точке. Окончательная выходная оценка сети получается как взвешенное среднее выходов по всем обучающим наблюдениям, где величины весов отражают расстояние от этих наблюдений до той точки, в которой производится оценивание (и, таким образом, более близкие точки вносят больший вклад в оценку). Первый промежуточный слой сети GRNN состоит из радиальных элементов.


Второй промежуточный слой содержит элементы, которые помогают оценить взвешенное среднее. Для этого используется специальная процедура. Каждый выход имеет в этом слое свой элемент, формирующий для него взвешенную сумму. Чтобы получить из взвешенной суммы взвешенное среднее, эту сумму нужно поделить на сумму весовых коэффициентов. Последнюю сумму вычисляет специальный элемент второго слоя. После этого в выходном слое производится собственно деление (с помощью специальных элементов "деления"). Таким образом, число элементов во втором промежуточном слое на единицу больше, чем в выходном слое. Как правило, в задачах регрессии требуется оценить одно выходное значение, и, соответственно, второй промежуточный слой содержит два элемента.

Можно модифицировать GRNN-сеть таким образом, чтобы радиальные элементы соответствовали не отдельным обучающим случаям, а их кластерам. Это уменьшает размеры сети и увеличивает скорость обучения. Центры для таких элементов можно выбирать с помощью любого предназначенного для этой цели алгоритма (выборки из выборки, K-средних или Кохонена), и программа ST Neural Networks соответствующим образом корректирует внутренние веса.

Достоинства и недостатки у сетей GRNN в основном такие же, как и у сетей PNN - единственное различие в том, что GRNN используются в задачах регрессии, а PNN - в задачах классификации. GRNN-сеть обучается почти мгновенно, но может получиться большой и медленной (хотя здесь, в отличие от PNN, не обязательно иметь по одному радиальному элементу на каждый обучающий пример, их число все равно будет большим). Как и сеть RBF, сеть GRNN не обладает способностью экстраполировать данные.

В начало

Линейная сеть
Линейная сеть

Согласно общепринятому в науке принципу, если более сложная модель не дает лучших результатов, чем более простая, то из них следует предпочесть вторую. В терминах аппроксимации отображений самой простой моделью будет линейная, в которой подгоночная функция определяется гиперплоскостью. В задаче классификации гиперплоскость размещается таким образом, чтобы она разделяла собой два класа (линейная дискриминантная функция); в задаче регрессии гиперплоскость должна проходить через заданные точки.


Линейная модель обычно записывается с помощью матрицы NxN и вектора смещения размера N. На языке нейронных сетей линейная модель представляется сетью без промежуточных слоев, которая в выходном слое содержит только линейные элементы (то есть элементы с линейной функцией активации). Веса соответствуют элементам матрицы, а пороги - компонентам вектора смещения. Во время работы сеть фактически умножает вектор входов на матрицу весов, а затем к полученному вектору прибавляет вектор смещения.

В пакете ST Neural Networks имеется возможность создать линейную сеть и обучить ее с помощью стандартного алгоритма линейной оптимизации, основанного на псевдообратных матрицах (SVD) (Golub and Kahan, 1965). Разумеется, метод линейной оптимизации реализован также в модуле Множественная регрессия системы STATISTICA; однако, линейные сети пакета ST Neural Networks имеют то преимущество, что здесь Вы можете в единой среде сравнивать такие сети с "настоящими" нейронными сетями.

Линейная сеть является хорошей точкой отсчета для оценки качества построенных Вами нейронных сетей. Может оказаться так, что задачу, считавшуюся очень сложной, можно успешно не только нейронной сетью, но и простым линейным методом. Если же в задаче не так много обучающих данных, то, вероятно, просто нет оснований использовать более сложные модели.

В начало

Сеть Кохонена
Сеть Кохонена

Сети Кохонена принципиально отличаются от всех других типов сетей, реализованных в пакете ST Neural Networks. В то время как все остальные сети предназначены для задач с управляемым обучением, сети Кохонена главным образом рассчитана на неуправляемое обучение (Kohonen, 1982; Haykin, 1994; Patterson, 1996; Fausett, 1994). При управляемом обучении наблюдения, составляющие обучающие данные, вместе с входными переменными содержат также и соответствующие им выходные значения, и сеть должна восстановить отображение, переводящее первые во вторые. В случае же неуправляемого обучения обучающие данные содержат только значения входных переменных.



На первый взгляд это может показаться странным. Как сеть сможет чему-то научиться, не имея выходных значений? Ответ заключается в том, что сеть Кохонена учится понимать саму структуру данных.

Одно из возможных применений таких сетей - разведочный анализ данных. Сеть Кохонена может распознавать кластеры в данных, а также устанавливать близость классов. Таким образом пользователь может улучшить свое понимание структуры данных, чтобы затем уточнить нейросетевую модель. Если в данных распознаны классы, то их можно обозначить, после чего сеть сможет решать задачи классификации. Сети Кохонена можно использовать и в тех задачах классификации, где классы уже заданы, - тогда преимущество будет в том, что сеть сможет выявить сходство между различными классами.

Другая возможная область применения - обнаружение новых явлений. Сеть Кохонена распознает кластеры в обучающих данных и относит все данные к тем или иным кластерам. Если после этого сеть встретится с набором данных, непохожим ни на один из известных образцов, то она не сможет классифицировать такой набор и тем самым выявит его новизну.

Сеть Кохонена имеет всего два слоя: входной и выходной, составленный из радиальных элементов (выходной слой называют также слоем топологической карты). Элементы топологической карты располагаются в некотором пространстве - как правило двумерном (в пакете ST Neural Networks реализованы также одномерные сети Кохонена).

Обучается сеть Кохонена методом последовательных приближений. Начиная со случайным образом выбранного исходного расположения центров, алгоритм постепенно улучшает его так, чтобы улавливать кластеризацию обучающих данных. В некотором отношении эти действия похожи на алгоритмы выборки из выборки и K-средних, которые используются для размещения центров в сетях RBF и GRNN, и действительно, алгоритм Кохонена можно использовать для размещения центров в сетях этих типов. Однако, данный алгоритм работает и на другом уровне.

Помимо того, что уже сказано, в результате итеративной процедуры обучения сеть организуется таким образом, что элементы, соответствующие центрам, расположенным близко друг от друга в пространстве входов, будут располагаться близко друг от друга и на топологической карте.


Топологический слой сети можно представлять себе как двумерную решетку, которую нужно так отобразить в N-мерное пространство входов, чтобы по возможности сохранить исходную структуру данных. Конечно же, при любой попытке представить N-мерное пространство на плоскости будут потеряны многие детали; однако, такой прием иногда полезен, так как он позволяет пользователю визуализировать данные, которые никаким иным способом понять невозможно.

Основной итерационный алгоритм Кохонена последовательно проходит одну за другой ряд эпох, при этом на каждой эпохе он обрабатывает каждый из обучающих примеров, и затем применяет следующий алгоритм: Выбрать выигравший нейрон (то есть тот, который расположен ближе всего к входному примеру); Скорректировать выигравший нейрон так, чтобы он стал более похож на этот входной пример (взяв взвешенную сумму прежнего центра нейрона и обучающего примера). В алгоритме при вычислении взвешенной суммы используется постепенно убывающий коэффициент скорости обучения, с тем чтобы на каждой новой эпохе коррекция становилась все более тонкой. В результате положение центра установится в некоторой позиции, которая удовлетворительным образом представляет те наблюдения, для которых данный нейрон оказался выигравшим.

Свойство топологической упорядоченности достигается в алгоритме с помощью дополнительного использования понятия окрестности. Окрестность - это несколько нейронов, окружающих выигравший нейрон. Подобно скорости обучения, размер окрестности убывает со временем, так что вначале к ней принадлежит довольно большое число нейронов (возможно, почти вся топологическая карта); на самых последних этапах окрестность становится нулевой (т.е. состоящей только из самого выигравшего нейрона). На самом деле в алгоритме Кохонена корректировка применяется не только к выигравшему нейрону, но и ко всем нейронам из его текущей окрестности.

Результатом такого изменения окрестностей является то, что изначально довольно большие участки сети "перетягиваются" - и притом заметно - в сторону обучающих примеров.


Сеть формирует грубую структуру топологического порядка, при которой похожие наблюдения активируют группы близко лежащих нейронов на топологической карте. С каждой новой эпохой скорость обучения и размер окрестности уменьшаются, тем самым внутри участков карты выявляются все более тонкие различия, что в конце концов приводит к тонкой настройке каждого нейрона. Часто обучение умышленно разбивают на две фазы: более короткую, с большой скоростью обучения и большими окрестностями, и более длинную с малой скоростью обучения и нулевыми или почти нулевыми окрестностями.

После того, как сеть обучена распознаванию структуры данных, ее можно использовать как средство визуализации при анализе данных. С помощью данных, выводимых в окне Частоты выигрышей - Win Frequencies , (где для каждого нейрона подсчитывается, сколько раз он выигрывал при обработке обучающих примеров), можно определить, разбивается ли карта на отдельные кластеры. Можно также обрабатывать отдельные наблюдения и смотреть, как при этом меняется топологическая карта, - это позволяет понять, имеют ли кластеры какой-то содержательный смысл (как правило при этом приходится возвращаться к содержательному смыслу задачи, чтобы установить, как соотносятся друг с другом кластеры наблюдений). После того, как кластеры выявлены, нейроны топологической карты помечаются содержательными по смыслу метками (в некоторых случаях помечены могут быть и отдельные наблюдения). После того, как топологическая карта в описанном здесь виде построена, на вход сети можно подавать новые наблюдения. Если выигравший при этом нейрон был ранее помечен именем класса, то сеть осуществляет классификацию. В противном случае считается, что сеть не приняла никакого решения.

При решении задач классификации в сетях Кохонена используется так называемый порог доступа. Ввиду того, что в такой сети уровень активации нейрона есть расстояние от него до входного примера, порог доступа играет роль максимального расстояния, на котором происходит распознавание.


Если уровень активации выигравшего нейрона превышает это пороговое значение, то сеть считается не принявшей никакого решения. Поэтому, когда все нейроны помечены, а пороги установлены на нужном уровне, сеть Кохонена может служить как детектор новых явлений (она сообщает о непринятии решения только в том случае, если поданный ей на вход случай значительно отличается от всех радиальных элементов).

Идея сети Кохонена возникла по аналогии с некоторыми известными свойствами человеческого мозга. Кора головного мозга представляет собой большой плоский лист (площадью около 0.5 кв.м.; чтобы поместиться в черепе, она свернута складками) с известными топологическими свойствами (например, участок, ответственный за кисть руки, примыкает к участку, ответственному за движения всей руки, и таким образом все изображение человеческого тела непрерывно отображается на эту двумерную поверхность).

В начало

Решение задач классификации в пакете ST Neural Networks
Решение задач классификации в пакете ST Neural Networks

В задаче классификации сеть должна отнести каждое наблюдение к одному из нескольких классов (или, в более общем случае, оценить вероятность принадлежности наблюдения к каждому из классов). В пакете ST Neural Networks для классификации используется номинальная выходная переменная - различные ее значения соответствуют различным классам. В пакете ST Neural Networks классификацию можно осуществлять с помощью сетей следующих типов: многослойного персептрона, радиальной базисной функции, сети Кохонена, вероятностной нейронной сети и линейной сети. Единственная из сетей пакета ST Neural Networks , не предназначенная для задач классификации, - это обобщенно-регрессионная сеть (на самом деле, если Вы потребуете, GRNNs будет пытаться это сделать, но мы этого не рекомендуем).

Номинальные переменные представляются в пакете ST Neural Networks в одном из двух видов ( первый из них годится только для переменных с двумя значениями): 1) бинарном (два состояния) и 2) один-из-N.


При бинарном представлении переменной соответствует один узел сети, при этом значение 0.0 означает активное состояние, а 1.0 - неактивное. При кодировании 1-из-N на каждое состояние выделяется один элемент, так что каждое конкретное состояние представляется как 1.0 в соответствующем элементе и 0.0 во всех других.

Номинальные входные переменные в пакете ST Neural Networks могут быть преобразованы одним из этих методов как на этапе обучения сети, так и при ее работе. Целевые выходные значения для элементов, соответствующих номинальным переменным, также легко определяются во время обучения. Несколько большие усилия требуются на то, чтобы по результатам работы сети определить выходной класс.

Каждый из выходных элементов будет содержать числовые значения в интервале от 0.0 до 1.0. Чтобы уверенно определить класс по набору выходных значений, сеть должна решить, "достаточно ли близки" они к нулю или единице. Если такой близости не наблюдается, класс считается "неопределенным".

Кроме того, в пакете ST Neural Networks для интерпретации выходных значений используются доверительные уровни (пороги принятия и отвержения). Эти пороговые значения можно корректировать, чтобы заставить сеть быть более или, наоборот, менее "решительной" при объявлении класса. Схемы здесь немного различаются для случаев бинарного и 1-из-N представлений:

Бинарное.
Бинарное.

Если выходное значение элемента превышает порог принятия, то выбирается класс 1.0. Если выходное значение лежит ниже порога отвержения, выбирается класс 0.0. Если выходное значение лежит между порогами, класс считается не определенным.

Один -из-N.
Один -из-N.

Определенный класс выбирается только в том случае, если значение соответствующего выходного элемента выше порога принятия, а всех остальных выходных элементов - ниже порога отвержения. Если же данное условие не выполнено, класс не определяется.

При кодировании методом 1-из-N имеет место одна особенность. На первый взгляд кажется, что "наиболее решительной" будет сеть с порогами принятия и отвержения, равными 0.5.


Это действительно так для бинарного кодирования, но уже не так для кодирования 1-из-N. Можно сделать так, чтобы порог принятия был ниже порога отвержения, и наиболее решительной будет сеть, у которой порог принятия 0.0 , а порог отвержения 1.0. При такой, на первый взгляд странной настройке сети элемент с наивысшим уровнем активации будет определять класс вне зависимости от того, что происходит в других элементах. Вот точная схема действия алгоритма определения класса в пакете ST Neural Networks: Выбирается элемент с наивысшим выходным сигналом. Если его выходной сигнал выше или равен порогу принятия, а выходные сигналы всех остальных элементов ниже порога отвержения, то в качестве ответа выдать класс, определяемый этим элементом. При пороге принятия 0.0 выходной сигнал выигравшего элемента всегда будет принят, а при пороге отвержения 1.0 все остальные элементы неизбежно будут отвергнуты, и поэтому алгоритм сводится к простому выбору выигравшего элемента. Если же оба пороговых значения - принятия и отвержения - установить на уровне 0.5, сеть вполне может остаться в нерешительности (в случаях, когда у победителя результат ниже 0.5 или у кого-то из проигравших - выше 0.5).

Хотя для понимания описанной процедуры требуются определенные усилия, после того, как Вы к ней привыкнете, Вы сможете устанавливать для задачи различные тонкие условия. Например, уровни принятия/отвержения, равные 0.3/0.7 , означают следующее: "выбрать класс, соответствующий выигравшему элементу, при условии, что его выход был не ниже 0.3 и ни у какого другого элемента активация не превышала 0.7" - другими словами, для того, чтобы решение было принято, победитель должен показать заметный уровень активации, а проигравшие - не слишком высокий.

Все сказанное относится к механизму выбора класса для большинства типов сетей: MLP, RBF, линейных сетей и PNN (одно исключение: в PNN-сети нельзя использовать бинарное кодирование, и даже бинарные номинальные выходные переменные оцениваются с помощью кодирования 1-из-N ).


В отличие от них, сеть Кохонена действует совершенно иначе.

В сети Кохонена выигравшим элементом топологической карты (выходного слоя) является тот, у которого самый высокий уровень активации (он измеряет расстояние от входного примера до точки, координаты которой хранятся в элементе сети). Некоторые или даже все элементы топологической карты могут быть помечены именами классов. Если это расстояние достаточно мало, то данный случай причисляется к соответствующему классу (при условии, что указано имя класса). В пакете ST Neural Networks значение порога принятия - это наибольшее расстояние, на котором принимается положительное решение о классификации наблюдения. Если же входной случай лежит от выигравшего элемента на более далеком расстоянии или если выигравший элемент не был помечен (или если его метка не соответствует ни одному из значений выходной номинальной переменной), то случай остается нерасклассифицированным. Порог отвержения в сетях Кохонена не используется.

В наших рассмотрениях мы предполагали, что "положительному" решению о классификации должно соответствовать значение, близкое к 1.0, а "отрицательному" - близкое к 0.0. Это действительно так в том случае, если на выходе используются логистические функции активации. Кроме того, это удобно, поскольку вероятность может принимать значения от 0.0 до 1.0. Однако, в некоторых ситуациях может оказаться более удобным использовать другой диапазон. Иногда применяется обратная упорядоченность, так что положительное решение соответствует малым выходным значениям. Пакет ST Neural Networks поддерживает любой из этих вариантов работы.

Вначале в качестве границ диапазона для каждой переменной используются значения минимум/среднее и максимум/стандартное отклонение. Для логистической выходной функции активации хорошими значениями по умолчанию являются 0.0 и 1.0. Некоторые авторы советуют использовать в качестве функции активации гиперболический тангенс, который принимает значения в интервале (-1.0,+1.0) .


Таким приемом можно улучшить обучение, потому что эта функция (в отличие от логистической) симметрична. В этом случае нужно изменить значения минимум/среднее и максимум/стандартное отклонение, и программа ST Neural Networks автоматически будет правильно интерпретировать классы.

Обратная упорядоченность, как правило, применяется в двух ситуациях. Одну из них мы только что обсудили: это сети Кохонена, в которых выходное значение есть мера удаленности, и ее малое значение соответствует большему доверию. Вторая ситуация возникает при использовании матрицы потерь (которая может быть добавлена в вероятностную сеть на этапе ее построения или вручную - к сетям других типов). Если используется матрица потерь, то выходы сети означают ожидаемые потери от выбора того или иного класса, и цель заключается в том, чтобы выбрать класс с наименьшими потерями. Упорядоченность можно обратить, объявив выходной сигнал не уровнем доверия, а мерой ошибки. В таком случае порог принятия будет ниже порога отвержения.

Таблица статистик классификации
Таблица статистик классификации

При выборе порогов принятия/отвержения и оценке способностей сети к классификации очень помогает информация, содержащаяся в окне Статистики классификации - Classification Statistics. В нем указывается, сколько наблюдений было классифицировано правильно, сколько неправильно или вообще не классифицировано. Кроме того, выдается информация о том, сколько наблюдений каждого класса было отнесено к другим классам. Все эти данные выдаются отдельно для обучающего, контрольного и тестового множеств.

В начало

Решение задач регрессии в пакете ST Neural Networks
Решение задач регрессии в пакете ST Neural Networks

В задачах регрессии целью является оценка значения числовой (принимающей непрерывный диапазон значений) выходной переменной по значениям входных переменных. Задачи регрессии в пакете ST Neural Networks можно решать с помощью сетей следующих типов: многослойный персептрон, радиальная базисная функция, обобщенно-регрессионная сеть и линейная сеть.


При этом выходные данные должны иметь стандартный числовой (не номинальный) тип. Особую важность для регрессии имеют масштабирование (шкалирование) выходных значений и эффекты экстраполяции.

Нейронные сети наиболее часто используемых архитектур выдают выходные значения в некотором определенном диапазоне (например, на отрезке [0,1] в случае логистической функции активации). Для задач классификации это не создает трудностей. Однако для задач регрессии совершенно очевидно, что тут есть проблема, и некоторые ее детали оказываются весьма тонкими. Сейчас мы обсудим возникающие здесь вопросы.

Для начала применим алгоритм масштабирования, чтобы выход сети имел "приемлемый" диапазон. Простейшей из масштабирующих функций пакета ST Neural Networks является минимаксная функция: она находит минимальное и максимальное значение переменной по обучающему множеству и выполняет линейное преобразование (с применением коэффициента масштаба и смещения), так чтобы значения лежали в нужном диапазоне (как правило, на отрезке [0.0,1.0]). Если эти действия применяются к числовой (непрерывной) выходной переменной, то есть гарантия, что все обучающие значения после преобразования попадут в область возможных выходных значений сети, и следовательно сеть может быть обучена. Кроме того, мы знаем, что выходы сети должны находиться в определенных границах. Это обстоятельство можно считать достоинством или недостатком - здесь мы приходим к вопросам экстраполяции.

Посмотрим на рисунок.



Мы стремимся оценить значение Y по значению X. Необходимо аппроксимировать кривую, проходящую через заданные точки. Вероятно, вполне подходящей для этого покажется кривая, изображенная на графике - она (приблизительно) имеет нужную форму и позволяет оценить значение Y в случае, если входное значение лежит в интервале, который охватывается сплошной частью кривой - в этой области возможна интерполяция.

Но что делать, если входное значение расположено существенно правее имеющихся точек? В таких случаях возможны два подхода к оценке значения Y.


Первый вариант - экстраполяция: мы продолжаем подогнанную кривую вправо. Во втором варианте мы говорим, что у нас нет достаточной информации для осмысленной оценки этого значения, и потому в качестве оценки мы принимаем среднне значение всех выходов (в отсутствие какой-либо информации это может оказаться лучшим выходом из положения).

Предположим, например, что мы используем многослойный персептрон (MLP). Применение минимакса по описанной выше схеме весьма ограничительно. Во-первых, кривая не будет экстраполироваться, как бы близко мы не находились к обучающим данным (в действительности же, если мы лишь чуть-чуть вышли за область обучающих данных, экстраполяция вполне оправдана). Во-вторых, оценка по среднему также не будет выполняться: вместо этого будет браться минимум или максимум смотря по тому, росла или убывала в этом месте оцениваемая кривая.

Чтобы избежать этих недостатков в MLP используется ряд приемов:

Во-первых, логистическую функцию активации в выходном слое можно заменить на линейную, которая не меняет уровня активации (N.B.: функции активации меняются только в выходном слое; в промежуточных слоях по-прежнему остаются логистические и гиперболические функции активации). Линейная функция активации не насыщается, и поэтому способна экстраполировать (при этом логистические функции предыдущих уровней все-таки предполагают насыщение на более высоких уровнях). Линейные функции активации в MLP могут вызвать определенные вычислительные трудности в алгоритме обратного распространения, поэтому при его использовании следует брать малые (менее 0.1) скорости обучения. Описанный подход пригоден для целей экстраполяции.

Во-вторых, можно изменить целевой диапазон минимаксной масштабирующей функции (например, сделать его [0.25,0.75]). В результате обучающие наблюдения будут отображаться в уровни, соответствующие средней части диапазона выходных значений. Интересно заметить, что если этот диапазон выбран маленьким, и обе его границы находятся вблизи значения 0.5, то он будет соответствовать среднему участку сигмоидной кривой, на котором она "почти линейна", - тогда мы будем иметь практически ту же схему, что и в случае линейного выходного слоя.


Такая сеть сможет выполнять экстраполяцию в определенных пределах, а затем будет насыщаться. Все это можно хорошо себе представить так: экстраполяция допустима в определенных границах, а вне их она будет пресекаться.

Если применяется первый подход и в выходном слое помещены линейные элементы, то может получиться так, что вообще нет необходимости использовать алгоритм масштабирования, поскольку элементы и без масштабирования могут выдавать любой уровень выходных сигналов. В пакете ST Neural Networks имеется возможность для большей эффективности вообще отключить все масштабирования. Однако, на практике полный отказ от масштабирования приводит к трудностям в алгоритмах обучения. Действительно, в этом случае разные веса сети работают в сильно различающихся масштабах, и это усложняет начальную инициализацию весов и (частично) обучение. Поэтому мы не рекомендуем Вам отключать масштабирование, за исключением тех случаев, когда диапазон выходных значений очень мал и расположен вблизи нуля. Это же соображение говорит в пользу масштабирования и при пре-процессировании в MLP-сетях (при котором, в принципе, веса первого промежуточного слоя можно легко корректировать, добиваясь этим любого нужного масштабирования).

До сих пор в нашем обсуждении мы уделяли основное внимание тому, как в задачах регрессии применяются сети MLP, и в особенности тому, как сети такого типа ведут себя в смысле экстраполяции. Сети, в которых используются радиальные элементы (RBF и GRNN), работают совершенно иначе и о них следует поговорить отдельно.

Радиальные сети по самой своей природе неспособны к экстраполяции. Чем дальше входной пример расположен от точек, соответствующих радиальным элементам, тем меньше становятся уровни активации радиальных элементов и (в конце концов) тем меньше будет выходной сигнал сети. Входной пример, расположенный далеко от центров радиальных элементов, даст нулевой выходной сигнал. Стремление сети не экстраполировать данные можно считать достоинством (это зависит от предметной области и Вашего мнения), однако убывание выходного сигнала (на первый взгляд) достоинством не является.


Если мы стремимся избегать экстраполяции, то для входных точек, отличающихся большой степенью новизны, в качестве выхода мы, как правило, хотим иметь усредненное значение.

Для радиальных сетей в задачах регрессии этого можно достичь с помощью масштабирующей функции среднее/стандартное отклонение. Обучающие данные масштабируются таким образом, чтобы среднее выходное значение равнялось 0.0, а все другие значения были бы промасштабированы на стандартное отклонение выходных сигналов. При обработке входных точек, лежащих вне областей действия радиальных элементов, выходной сигнал сети будет приблизительно равен среднему значению.

Качество работы сети в задаче регрессии можно проверить несколькими способами.

Во-первых, сети можно сообщить выходное значение, соответствующее любому наблюдению (или какому-то новому наблюдению, который Вы хотели бы проверить). Если это наблюдение содержалось в исходных данных, то выдается значение разности (невязки).

Во-вторых, могут быть получены итоговые статистики. К ним относятся среднее значение и стандартное отклонение, вычисленные для обучающих данных и для ошибки прогноза. В общем случае среднее значение ошибки прогноза будет очень близко к нулю (в конце концов, нулевое среднее для ошибки прогноза можно получить, попросту оценив среднее значение обучающих данных и вовсе не обращаясь к значениям входных переменных). Наиболее важным показателем является стандартное отклонение ошибки прогноза. Если оно не окажется существенно меньше стандартного отклонения обучающих данных, это будет означать, что сеть работает не лучше, чем простая оценка по среднему. Далее, в пакете ST Neural Networks пользователю выдается отношение стандартного отклонения ошибки прогноза к стандартному отклонению обучающих данных. Если оно существенно меньше единицы (например, ниже 0.1), то это говорит о хорошем качестве регрессии. Это регрессионное отношение (точнее, величину единица минус это отношение) иногда называют долей объясненной дисперсии модели.

В-третьих, можно вывести изображение поверхности отклика.


На самом деле, разумеется, эта поверхность представляет собой N+1-мерный объект, где N - число входных элементов, а оставшееся измерение соответствует высоте точки на поверхности. Понятно, что непосредственно визуально представить такую поверхность при N большем двух невозможно (а реально N всегда больше двух). Тем не менее, в пакете ST Neural Networks Вы можете выводить срезы поверхности отклика по любым двум входным переменным. При этом значения всех остальных входных переменных фиксируются, и меняются только два выбранные. Всем остальным переменным можно придать любое значение по своему усмотрению (по умолчанию система ST Neural Networks возьмет для них средние значения). Значения двух исследуемых переменных можно менять в произвольном диапазоне (по умолчанию - в диапазоне изменения обучающих данных).

В начало

Прогнозирование временных рядов в пакете ST Neural Networks
Прогнозирование временных рядов в пакете ST Neural Networks

В задачах анализа временных рядов целью является прогноз будущих значений переменной, зависящей от времени, на основе предыдущих значений ее и/или других переменных (Bishop, 1995) Как правило, прогнозируемая переменная является числовой, поэтому прогнозирование временных рядов - это частный случай регрессии. Однако такое ограничение не заложено в пакет ST Neural Networks, так что в нем можно прогнозировать и временные ряды номинальных (т.е. классифицирующих) переменных.

Обычно очередное значение временного ряда прогнозируется по некоторому числу его предыдущих значений (прогноз на один шаг вперед во времени). В пакете ST Neural Networks можно выполнять прогноз на любое число шагов. После того, как вычислено очередное предполагаемое значение, оно подставляется обратно и с его помощью (а также предыдущих значений) получается следующий прогноз - это называется проекцией временного ряда. В пакете ST Neural Networks можно осуществлять проекцию временного ряда и при пошаговом прогнозировании. Понятно, что надежность такой проекции тем меньше, чем больше шагов вперед мы пытаемся предсказать.


В случаях, когда требуется совершенно определенная дальность прогноза, разумно будет специально обучить сеть именно на такую дальность.

В пакете ST Neural Networks для решения задач прогноза временных рядов можно применять сети всех типов (тип сети должен подходить, в зависимости от задачи, для регрессии или классификации). Сеть конфигурируется для прогноза временного ряда установкой параметров Временное окно - Steps и Горизонт - Lookahead. Параметр Временное окно задает число предыдущих значений, которые следует подавать на вход, а параметр Горизонт указывает, как далеко нужно строить прогноз. Количество входных и выходных переменных может быть произвольным. Однако, чаще всего в качестве входной и одновременно (с учетом горизонта) выходной выступает единственная переменная. При конфигурировании сети для анализа временных рядов изменяется метод пре-процессирования данных (извлекаются не отдельные наблюдения, а их блоки), но обучение и работа сети происходят точно так же, как и в задачах других типов.

В задачах анализа временных рядов обучающее множество данных, как правило, бывает представлено значениями одной переменной, которая является входной/выходной (т.е. служит для сети и входом, и выходом).

В задачах анализа временных рядов особую сложность представляет интерпретация понятий обучающего, контрольного и тестового множеств, а также неучитываемых данных. В обычной ситуации каждое наблюдение рассматривается независимо, и никаких вопросов здесь не возникает. В случае же временного ряда каждый входной или выходной набор составлен из данных, относящихся к нескольким наблюдениям, число которых задается параметрами сети Временное окно - Steps и Горизонт - Lookahead. Из этого следуют два обстоятельства:

Категория, которое будет отнесен набор, определяется категорией выходного наблюдения. Например, если в исходных данных первые два наблюдения не учитываются, а третье объявлено тестовым, и значения параметров Временное окно и Горизонт равны соответственно 2 и 1, то первый используемый набор будет тестовым, его входы будут браться из первых двух наблюдений, а выход - из третьего.


Таким образом, первые два наблюдения, хотя и помечены как не учитываемые, используются в тестовом множестве. Более того, данные одного наблюдения могут использоваться сразу в трех наборах, каждый из которых может быть обучающим, контрольным или тестовым. Можно сказать, что данные "растекаются" по обучающему, контрольному и тестовому множествам. Чтобы полностью разделить эти множества, пришлось бы сформировать отдельные блоки обучающих, контрольных и тестовых наблюдений, отделенные друг от друга достаточным числом неучитываемых наблюдений.

Несколько первых наблюдений можно использовать только в качестве входных данных. При выборе наблюдений во временном ряду номер наблюдения всегда соответствует выходному значению. Поэтому первые несколько наблюдений вообще невозможно выбрать (для этого были бы нужны еще несколько наблюдений, расположенных перед первым наблюдением в исходных данных), и они автоматически помечаются как неучитываемые.

В начало

Отбор переменных и понижение размерности
Отбор переменных и понижение размерности

До сих пор, говоря о построении и конструировании сети, мы предполагали, что входной и выходной слои заданы, то есть, что мы уже знаем, какие переменные будут подаваться на вход сети, и что будет ее выходом. То, какие переменные будут выходными, известно всегда (по крайней мере в случае управляемого обучения). Что же касается входных переменных, их правильный выбор порой представляет большие трудности (Bishop, 1995). Часто мы не знаем заранее, какие из входных переменных действительно полезны для решения задачи, и выбор хорошего множества входов бывает затруднен целым рядом обстоятельств: Проклятие размерности. Каждый дополнительный входной элемент сети - это новая размерность в пространстве данных. С этой точки зрения становится понятно следующее: чтобы достаточно плотно "заселить" N-мерное пространство и "увидеть" структуру данных, нужно иметь довольно много точек. Необходимое число точек быстро возрастает с ростом размерности пространства (грубо говоря, как 2**N для большинства методов).


Большинство типов нейронных сетей ( в частности, многослойный персептрон MLP) в меньшей степени страдают от проклятия размерности, чем другие методы, потому что сеть умеет следить за проекциями участков многомерного пространства в пространства малой размерности (например, если все веса, выходящие из некоторого входного элемента, равны нулю, то MLP-сеть полностью игнорирует эту входную переменную). Тем не менее, проклятие размерности остается серьезной проблемой, и качество работы сети можно значительно улучшить, исключив ненужные входные переменные. На самом деле, чтобы уменьшить эффект проклятия размерности иногда бывает целесообразно исключить даже те входные переменные, которые несут в себе некоторою (небольшую) информацию. Внутренние зависимости между переменными. Было бы очень хорошо, если бы каждую переменную - кандидата на то, чтобы служить входом сети, можно было бы независимо оценить на "полезность", а затем отобрать самые полезные переменные. К сожалению, как правило, это бывает невозможно сделать, и две или более взаимосвязанных переменных могут вместе нести существенную информацию, которая не содержится ни в каком их подмножестве. Классическим примером может служить задача с двумя спиралями, в которой точки данных двух классов расположены вдоль двух переплетающихся двумерных спиралей. Ни одна из переменных в отдельности не несет никакой полезной информации (классы будут выглядеть совершенно перемешанными), но глядя на обе переменные вместе, классы легко разделить. Таким образом, в общем случае переменные нельзя отбирать независимо. Избыточность переменных. Часто бывает так, что одна и та же информация в большей или меньшей степени повторяется в разных переменных. Например, данные о росте и весе человека, как правило, несут в себе сходную информацию, поскольку они сильно коррелированы. Может оказаться так, что в качестве входов достаточно взять лишь часть из нескольких коррелированных переменных, и этот выбор может быть произвольным. В таких ситуациях вместо всего множества переменных лучше взять их часть - этим мы избегаем проклятия размерности. Итак, выбор входных переменных - это исключительно важный этап при построении нейронной сети.


Перед тем, как непосредственно начинать работать с пакетом ST Neural Networks , имеет смысл произвести предварительный отбор переменных, используя при этом свои знания в предметной области и стандартные статистические критерии. Затем, уже средствами пакета ST Neural Networks можно будет попробовать различные комбинации входных переменных. В пакете ST Neural Networks имеется возможность "игнорировать" некоторые переменные, так что полученная сеть не будет использовать их в качестве входов. Можно поочередно экспериментировать с различными комбинациями входов, строя всякий раз новые варианты сетей. При таком экспериментировании очень полезными оказываются вероятностные и обобщенно-регрессионные сети. Несмотря на то, что они работают медленнее более компактных MLP и RBF сетей, они обучаются почти мгновенно, и это важно, поскольку при переборе большого числа комбинаций входных переменный приходится каждый раз строить новые сети. Кроме того, PNN и GRNN (как и RBF) - это радиальные сети (в первом слое они имеют радиальные элементы, и аппроксимирующие функция строятся в виде комбинаций гауссовых функций). При отборе входных переменных это является преимуществом, поскольку радиальные сети в меньшей степени страдают от проклятия размерности, чем сети, построенные на линейных элементах.

Чтобы понять причину этого, рассмотрим, что произойдет, если мы добавим в сеть новую, возможно совершенно несущественную входную переменную. Сеть на линейных элементах, например MLP, может научиться присваивать весам, идущим от этой переменной, нулевые значения, что означает игнорирование переменной (реально это происходит так: изначально малые веса этой переменной так и остаются малыми, а веса содержательных входных переменных меняются нужным образом). Радиальная сеть типа PNN или GRNN не может позволить себе такую роскошь: кластеры, образующиеся в пространстве небольшого числа существенных переменных, будут "размазаны" по направлениям несущественных размерностей - для учета разброса по несущественным направлениям требуется большее число элементов.


Сеть, в большей степени страдающая от наличия плохих входных данных, имеет преимущество, когда мы стремимся избавиться то этих плохих данных.

Поскольку описанный процесс экспериментирования занимает много времени, в пакете ST Neural Networks имеется инструмент, который может сделать это за Вас. Для выбора подходящей комбинации входных переменных здесь используется так называемый генетический алгоритм (Goldberg, 1989). Генетические алгоритмы хорошо приспособлены для задач такого типа, поскольку они позволяют производить поиск среди большого числа комбинаций при наличии внутренних зависимостей в переменных.

Существует и другой подход к проблеме размерности, который может использоваться как альтернатива или как дополнение к методам отбора переменных: это понижение размерности. Суть его состоит в том, что исходная совокупность переменных преобразуется в новую совокупность, состоящую из меньшего числа переменных, но при этом (как мы надеемся) содержащую по возможности всю информацию, заложенную в исходных данных. В качестве примера рассмотрим данные, все точки которых расположены на некоторой плоскости в трехмерном пространстве. Истинная размерность данных равна двум (поскольку вся информация на самом деле содержится в двумерном подпространстве). Если мы сумеем обнаружить эту плоскость, то на вход нейронной сети можно будет подавать входные данные меньшей размерности, и будет больше шансов на то, что такая сеть будет работать правильно.

Самый распространенный метод понижения размерности - это анализ главных компонент (Bishop, 1995; см. также  Факторный анализ). Метод состоит в следующем: к данным применяется линейное преобразование, при котором направлениям новых координатных осей соответствуют направления наибольшего разброса исходных данных. Как правило, уже первая компонента отражает большую часть информации, содержащейся в данных. Поскольку анализ главных компонент (АГК) представляет собой линейный метод, его можно реализовать с помощью линейной сети, и в пакете ST Neural Networks предусмотрена возможность обучать линейную сеть для выполнения АГК.


Очень часто метод АГК выделяет из многомерных исходных данных совсем небольшое число компонент, сохраняя при этом структуру информации.

Один из недостатков метода главных компонент (АГК) состоит в том, что это чисто линейный метод, и из-за этого он может не учитывать некоторые важные характеристики структуры данных. В пакете ST Neural Networks реализован также вариант "нелинейного АГК", основанный на использовании так называемой автоассоциативной сети (Bishop, 1995; Fausett, 1994; Bouland and Kamp, 1988). Это такая нейронная сеть, которую обучают выдавать в качестве выходов свои собственные входные данные, но при этом в ее промежуточном слое содержится меньше нейронов, чем во входном и выходном слоях. Поэтому, чтобы восстановить свои входные данные, сеть должна научиться представлять их в более низкой размерности. Сеть "впихивает" наблюдения в формат промежуточного слоя и только потом выдает их на выходе. После обучения автоассоциативной сети ее внешний интерфейс может быть сохранен и использован для понижения размерности. Как правило, в качестве автоассоциативной сети берется многослойный персептрон с тремя промежуточными слоями. При этом средний слой отвечает за представление данных в малой размерности, а два других скрытых слоя служат соответственно для нелинейного преобразования входных данных в средний слой и выходов среднего слоя в выходной слой. Автоассоциативная сеть с единственным промежуточным слоем может выполнять только линейное понижение размерности, и фактически осуществляет АГК в стандартном варианте.

В начало

(c) Copyright StatSoft, Inc., 1984-2001
STATISTICA является торговой маркой StatSoft, Inc.

Нелинейное оценивание

Нелинейное оценивание

Общее назначение Оценивание линейных и нелинейных моделей Основные типы нелинейных моделей Регрессионные модели с линейной структурой Существенно нелинейные регрессионные модели Методы нелинейного оценивания Метод наименьших квадратов Функция потерь Метод взвешенных наименьших квадратов Метод максимума правдоподобия Максимум правдоподобия и логит/пробит модели Алгоритмы минимизации функций Начальные значения, размеры шагов и критерий сходимости Штрафные функции, ограничение параметров Локальные минимумы Квази-ньютоновский метод Симплекс-метод Метод Хука-Дживиса Метод Розенброка Матрица Гессе и стандартные ошибки Оценивание пригодности модели Объясненная доля дисперсии Критерий согласия хи-квадрат График наблюдаемых и предсказанных значений Нормальный и полунормальный график остатков График функции подгонки Ковариационная матрица оценок параметров

 
  Общее назначение Оценивание линейных и нелинейных моделей Основные типы нелинейных моделей Регрессионные модели с линейной структурой Существенно нелинейные регрессионные модели Методы нелинейного оценивания Метод наименьших квадратов Функция потерь Метод взвешенных наименьших квадратов Метод максимума правдоподобия Максимум правдоподобия и логит/пробит модели Алгоритмы минимизации функций Начальные значения, размеры шагов и критерий сходимости Штрафные функции, ограничение параметров Локальные минимумы Квази-ньютоновский метод Симплекс-метод Метод Хука-Дживиса Метод Розенброка Матрица Гессе и стандартные ошибки Оценивание пригодности модели Объясненная доля дисперсии Критерий согласия хи-квадрат График наблюдаемых и предсказанных значений Нормальный и полунормальный график остатков График функции подгонки Ковариационная матрица оценок параметров

 

Общее назначение
Общее назначение

Иногда, при проведении анализа линейной модели, исследователь получает данные о ее неадекватности. В этом случае, его по-прежнему интересует зависимость между предикторными переменными и откликом, но для уточнения модели в ее уравнение добавляются некоторые нелинейные члены.
Самым удобным способом оценивания параметров полученной регрессии является Нелинейное оценивание. Например, его можно использовать для уточнения зависимости между дозой и эффективностью лекарства, стажем работы и производительностью труда, стоимостью дома и временем, необходимым для его продажи и т.д. Наверное, вы заметили, что ситуации, рассматриваемые в этих примерах, часто интересовали нас и в таких методах как множественная регрессия (см. Множественная регрессия) и дисперсионный анализ (см. Дисперсионный анализ). На самом деле, можно считать Нелинейное оценивание обобщением этих двух методов. Так, в методе множественной регрессии (и в дисперсионном анализе) предполагается, что зависимость отклика от предикторных переменных линейна. Нелинейное оценивание оставляет выбор характера зависимости за вами. Например, вы можете определить зависимую переменную как логарифмическую функцию от предикторной переменной, как степенную функцию, или как любую другую композицию элементарных функций от предикторов (однако, если все изучаемые переменные категориальны по своей природе, вы можете также воспользоваться модулем Анализ соответствий).

Если позволить рассмотрение любого типа зависимости между предикторами и переменной отклика, возникают два вопроса. Во-первых, как истолковать найденную зависимость в виде простых практических рекомендаций. С этой точки зрения линейная зависимость очень удобна, так как позволяет дать простое пояснение: “чем больше x (т.е., чем больше цена дома), тем больше y (тем больше времени нужно, чтобы его продать); и, задавая конкретные приращения x, можно ожидать пропорциональное приращение y”. Нелинейные соотношения обычно нельзя так просто проинтерпретировать и выразить словами. Второй вопрос - как проверить, имеется ли на самом деле предсказанная нелинейная зависимость.

Далее мы рассмотрим проблему нелинейной регрессии более формально и введем стандартную терминологию, позволяющую рассмотреть сущность этого метода более пристально. Мы также покажем примеры его использования в различных областях исследований: медицине, социологии, физике, химии, фармакологии, проектировании и т.д.

В начало

Оценивание линейных и нелинейных моделей
Оценивание линейных и нелинейных моделей

Формально говоря, модуль Нелинейное оценивание является универсальной аппроксимирующей процедурой, оценивающей любой вид зависимости между переменной отклика и набором независимых переменных. В общем случае, все регрессионные модели могут быть записаны в виде формулы:

y = F(x1, x2, ... , xn)

При проведении регрессионного, а в частности нелинейного регрессионного анализа, исследователя интересует, связана ли и если да, то как, зависимая переменная и набор независимых переменных. Выражение F(x...) в выписанном выше выражении означает, что переменная отклика y является функцией от независимой переменной x.

Примером модели такого типа может быть модель множественной линейной регрессии, описанная в разделе Множественная регрессия. В этой модели предполагается, что зависимая переменная является линейной функцией независимых переменных, т.е.:

y = a + b1*x1 + b2*x2 + ... + bn*xn

Если вы не знакомы с множественной линейной регрессией, вы можете прямо сейчас перечитать вводный обзор Множественной регрессии (но вам вовсе не обязательно понимать все нюансы множественной линейной регрессии, для того чтобы разобраться в обсуждаемом здесь методе).

Нелинейное оценивание позволяет задать практически любой тип непрерывной или разрывной регрессионной модели. Некоторые из наиболее общих нелинейных моделей (такие как пробит и логит модели, модель экспоненциального роста и регрессия с точками разрыва) уже имеются в Нелинейном оценивании. Однако, при необходимости, вы можете также самостоятельно ввести регрессионное уравнение любого типа, поручив программе его подгонку в соответствии с вашими данными. Более того, для оценивания модели вы можете использовать метод наименьших квадратов, метод максимума правдоподобия (если это допускается выбранной моделью), или, опять же, определить вашу собственную функцию потерь (см. ниже) задав соответствующее уравнение.

В общем случае, каждый раз, когда простая модель линейной регрессии неадекватно отражает зависимость переменных, используется модель нелинейной регрессии.


Выберите один из следующих разделов для получения более полного представления об основных типах нелинейных моделей, процедурах нелинейного оценивания и оценивании пригодности модели.

  Основные типы нелинейных моделей Регрессионные модели с линейной структурой Существенно нелинейные регрессионные модели
Основные типы нелинейных моделей Регрессионные модели с линейной структурой Существенно нелинейные регрессионные модели  

Регрессионные модели с линейной структурой Полиномиальная регрессия.
Полиномиальная регрессия.

Распространенной “нелинейной” моделью является модель полиномиальной регрессии. Термин нелинейная заключен в кавычки, поскольку эта модель линейна по своей природе. Например, предположим, что вы измеряете в обучающем эксперименте связь физиологического возбуждения объектов и их производительности в задаче слежения за целями. На основании хорошо известного закона Йеркса-Додсона, можно ожидать нелинейной зависимости между уровнем возбуждения и производительностью. Это предположение можно выразить следующим уравнением регрессии:

Производительность = a + b1*Возбуждение + b2*Возбуждение2

В этом уравнении, a представляет свободный член, а b1 и b2 коэффициенты регрессии. Нелинейность этой модели выражается членом Возбуждение2. Однако, в сущности, модель по-прежнему линейна, за исключением того, что при ее оценивании нам придется возводить наблюдаемый уровень возбуждения в квадрат. Для оценивания коэффициентов регрессии этой модели можно использовать фиксированное нелинейное оценивание. Такие модели, где мы составляем линейное уравнение из некоторых преобразований независимых переменных, относятся к моделям нелинейным по переменным.

Модели, нелинейные по параметрам.
Модели, нелинейные по параметрам.

Для сравнения с предыдущим примером рассмотрим зависимость между возрастом человека (переменная x) и его скоростью роста (переменная y). Очевидно, что соотношение между этими двумя переменными на первом году человеческой жизни (когда происходит наибольший рост) сильно отличается от соотношения во взрослом возрасте (когда человек почти не растет).


Поэтому, эту зависимость лучше представить в виде какой-нибудь экспоненциальной функции с отрицательным показателем степени:

Рост = exp(-b1*Возраст)

Если вы построите на графике оценку для коэффициента регрессии, то вы получите кривую следующего вида:



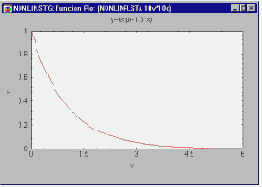
Отметим, что эта модель по своей природе больше не является линейной, т.е. выражение, написанное сверху, не представимо в виде простой регрессионной модели с некоторыми преобразованиями независимых переменных. Такие модели называются нелинейными по параметрам.

Сведение нелинейных моделей к линейным.
Сведение нелинейных моделей к линейным.

В общем случае, всегда, когда регрессионная модель может быть сведена к линейной модели, этому способу отдается предпочтение (при оценивании соответствующей модели). Модель линейной множественной регрессии (см. Множественная регрессия) наиболее просто понимаема с точки зрения математики и, с практической точки зрения, наиболее проста для толкования. Поэтому, возвращаясь к простой экспоненциальной регрессионной модели Скорости роста как функции Возраста, описанной раньше, мы можем преобразовать это нелинейное уравнение в линейное, прологарифмировав обе части уравнения, получив:

log(Рост) = -b1*Возраст

Если теперь заменить log(Рост)) на y, мы получим стандартную модель линейной регрессии, как уже было показано раньше (без свободного члена, который был опущен для простоты изложения). Таким образом, для оценивания взаимоотношения возраста и скорости роста вы можете прологарифмировать данные о скорости роста (например, воспользовавшись преобразованиями таблиц данных с помощью формул), а затем использовать Множественную регрессию, получив при этом интересующий нас коэффициент регрессии b1.

Адекватность модели.
Адекватность модели.

Конечно, используя “неправильное” преобразование, можно прийти к неадекватной модели. Поэтому, после ”линеаризации” модели, наподобие только что показанной, очень важно провести подробное изучение статистик остатков, вычисляемых с помощью Множественной регрессии.



Существенно нелинейные регрессионные модели

Для некоторых регрессионных моделей, которые не могут быть сведены к линейным, единственным способом для исследования остается Нелинейное оценивание. В приведенном выше примере для скорости роста, мы специально “забыли ” о случайной ошибке в зависимой переменной. Конечно, на скорость роста влияют множество других факторов (кроме возраста), и нам следует ожидать значительных случайных отклонений (остатков) от предложенной нами кривой. Если добавить эту ошибку или остаточную изменчивость, нашу модель можно переписать следующим образом:

Рост = exp(-b1*Возраст) + ошибка

Аддитивная ошибка.
Аддитивная ошибка.

В этой модели предполагается, что случайная ошибка не зависит от возраста, т.е., остаточная изменчивость одинакова для всех возрастов. Поскольку ошибка в этой модели аддитивна, т.е. просто прибавляется к точному значению скорости роста, мы больше не можем линеаризовать эту модель простым логарифмированием обеих частей. Если бы мы снова прологарифмировали входные данные о скорости роста и подобрали простую линейную модель, мы заметили бы, что остатки больше не являются равномерно распределенными вокруг значений переменной возраст; и поэтому, стандартный линейный регрессионный анализ (с помощью Множественной регрессии) больше не применим. Единственным способом оценивания параметров модели остается использование Нелинейного оценивания.

Мультипликативная ошибка.
Мультипликативная ошибка.

В “оправдание” предыдущего примера заметим, что в данном случае постоянство вариации случайной ошибки в любом возрасте мало вероятно, т.е., предположение об аддитивности ошибки не слишком реалистично. Правдоподобнее, что изменения скорости роста более случайны и непредсказуемы в раннем возрасте, чем в позднем, когда рост практически останавливается. Поэтому, более реалистичной моделью, включающей ошибку, будет:

Рост = exp(-b1*Возраст) * ошибка

На словах это означает, что чем больше возраст, тем меньше множитель exp(-b1*Возраст), и, следовательно, тем меньше будет разброс результирующей ошибки.


Если же вы теперь прологарифмируете обе части нашего уравнения, то остаточная ошибка перейдет в свободный член линейного уравнения, т.е., аддитивный фактор, и вы сможете продолжить и оценить b1 пользуясь стандартную множественную регрессию.

Log (Рост) = -b1*Возраст + ошибка

Теперь мы рассмотрим некоторые регрессионные модели (нелинейные по параметрам), которые не могут быть сведены к линейным простым преобразованием начальных данных.

Общая модель роста.
Общая модель роста.

Общая модель роста похожа на рассмотренный ранее пример:

y = b0 + b1*exp(b2*x) + ошибка

Эта модель обычно используется при изучении различных видов роста (y), когда скорость роста в любой момент времени (x) пропорциональна оставшемуся приросту. Параметр b0 в этой модели представляет максимальное значение скорости роста. Типичным примером ее адекватного использования служит описание концентрации вещества (например, в воде) в виде функции времени.

Модели бинарных откликов: пробит и логит.
Модели бинарных откликов: пробит и логит.

Нередко зависимая переменная - переменная отклика бинарна по своей природе, т.е. может принимать только два значения. Например, пациент может выздороветь, а может и нет, кандидат на должность может пройти, а может провалить тест при приеме на работу, подписчики журнала могут продлить, а могут не продлевать подписку, купоны скидок могут быть использованы, а могут быть и не использованы и т.п. Во всех этих случаях нас может заинтересовать поиск зависимости между одной или несколькими “непрерывными” переменными и одной, зависящей от них бинарной переменной.

Использование линейной регрессии. Конечно, можно использовать стандартную множественную регрессию и вычислить стандартные коэффициенты регрессии. Например, если рассматривается продление журнальной подписки, можно задать переменную y со значениями 1’ и 0’, где 1 означает, что соответствующий подписчик продлил подписку, а 0, что он отказался от продления. Однако здесь возникает проблема: Множественная регрессия не “знает”, что переменная отклика бинарна по своей природе.


Поэтому, это неизбежно приведет к модели с предсказываемыми значениями большими 1 и меньшими 0. Но такие значения вообще не допустимы для первоначальной задачи, таким образом, множественная регрессия просто игнорирует ограничения на диапазон значений для y.

Непрерывные функции отклика. Задача регрессии может быть сформулирована иначе: вместо предсказания бинарной переменной, мы предсказываем непрерывную переменную со значениями на отрезке [0,1]. Наибольшее распространение в этой области получили регрессионные модели логит и пробит.

Логит регрессия. В этой модели предсказываемые значения для зависимой переменной больше или равны 0 и меньше или равны 1 при любых значениях независимых переменных. Это достигается применением следующего регрессионного уравнения, которое в действительности имеет также некоторый глубокий смысл, как вы вскоре увидите (термин логит впервые был использован в работе Berkson, 1944):

y = exp(b0 + b1*x1 + ... + bn*xn)/{1 + exp(b0 + b1*x1 + ... + bn*xn)}

Легко заметить, что вне зависимости от коэффициентов регрессии и значений x, значения y, предсказанные этой моделью всегда будут принадлежать отрезку [0,1].

Название логит этой модели происходит от названия простого способа сведения этой модели к линейной с помощью логит преобразования. Предположим, что мы рассуждаем о нашей зависимой переменной в терминах нашей основной вероятности p, лежащей между 0 и 1. Тогда мы можем преобразовать эту вероятность p:

p' = loge{p/(1-p)}

Это преобразование обычно называют логистическим или логит - преобразованием. Отметим, что теоретически p’ может принимать любое значение от минус до плюс бесконечности. Поскольку логистическое преобразование решает проблему об ограничении на 0-1 границы для первоначальной зависимой переменной (вероятности), вы можете использовать эти (преобразованные) значения в обычном линейном регрессионном уравнении. А именно, если произвести логистическое преобразование обеих частей описанного выше уравнения, мы получим стандартную модель линейной регрессии:



p' = b0 + b1*x1 + b2*x2 + ... + bn*xn

Пробит регрессия.
Пробит регрессия.

Можно рассматривать бинарную зависимую переменную как отклик на изменения некоторой “основной”, нормально распределенной переменной, в действительности имеющую диапазон изменений от минус до плюс бесконечности. Например, подписчик журнала может быть решительно против продления подписки, находится в нерешительности или испытывать расположение к журналу и стремиться продлить подписку. В любом случае, все, что мы (как издатели журнала) увидим, будет бинарный отклик, означающий продление или отказ от продления подписки. Однако если мы запишем стандартное уравнение линейной регрессии, основанное на “отношении людей к журналу”, мы получим:

отношение... = b0 + b1*x1 + ...

что, конечно, соответствует стандартной регрессионной модели. Логично предположить, что это “отношение людей к журналу” нормально распределено, и что вероятность продления подписки p равна соответствующей “отношению к журналу ” площади под графиком плотности нормального распределения. Поэтому, если мы преобразуем обе части уравнения в соответствующие нормальные вероятности, мы получим:

NP(отношение...) = NP(b0 + b1*x1 + ...)

Здесь NP означает нормальную вероятность (площадь под графиком плотности нормального распределения), таблицы которой имеются практически в любом статистическом справочнике. Выписанное выше уравнение называется также регрессионной моделью пробит. (Термит пробит был впервые использован в работе Bliss, 1934.)

Обобщенная логит регрессия.
Обобщенная логит регрессия.

Обобщенная логит регрессия может быть выражена уравнением:

y = b0/{1 + b1*exp(b2*x)}

Вы можете представлять себе эту модель как обобщение обычной логит модели для бинарных зависимых переменных. Однако если логит модель ограничивает значения зависимой переменной только двумя возможными значениями, то общая модель позволяет отклику произвольно меняться внутри фиксированного интервала. Например, предположим, что вас интересует прирост популяции вида, перенесенного на новое место обитания, рассмотренный в виде функции времени.


Тогда зависимая переменная будет равна числу особей данного вида в соответствующей среде обитания. Очевидно, что ее значение ограничено снизу, так как число особей не может быть меньше нуля; вероятно, что также существует какой-то верхний предел для численности популяции, который будет достигнут в некоторый момент времени.

Восприимчивость к лекарству и полумаксимальный отклик
Восприимчивость к лекарству и полумаксимальный отклик

. В фармакологии, для описания эффективности различных доз лекарственных средств, часто используется следующая модель:

y = b0 - b0/{1 + (x/b2)b1}

В этой модели, x означает размер дозы (обычно в некоторой закодированной форме, так что x 1), а y соответствует восприимчивости, измеренной в процентах по отношению к максимально возможной. Параметр b0 тогда означает ожидаемый отклик при насыщающем уровне дозы, а b2 равен концентрации, вызывающей полумаксимальный отклик; параметр b1 определяет наклон графика предсказываемой функции.

Регрессионные модели сточками разрыва
Кусочно - линейная регрессия.
Регрессионные модели сточками разрыва
Кусочно - линейная регрессия.

Нередко вид зависимости между предикторами и переменной отклика различается в разных областях значений независимых переменных. Например, вы рассматриваете себестоимость единицы некоторого продукта как функцию от объема произведенной продукции за месяц. Обычно, чем больше единиц товара вы производите, тем ниже себестоимость каждой единицы, и эта линейная зависимость существует в широких пределах изменения объема произведенной продукции. Однако при прохождении кривой выпуска через некоторые значения себестоимость может меняться скачкообразно. Например, себестоимость может увеличиваться при увеличении объема производства из-за того, что для производства дополнительных единиц используются другие (устаревшие) станки. Допустим, что устаревшие машины используются в производстве при достижении объемом производства уровня 500 единиц в месяц; этой ситуации соответствует следующая регрессионную модель для себестоимости:



y = b0 + b1*x*(x 500) + b2*x*(x > 500)

В этой формуле: y означает оцениваемую себестоимость, а x равен объему продукции, произведенной за месяц. Выражения (x 500) и (x > 500) обозначают логические условия, принимающие значения 1 если они истинны, и 0 иначе. Таким образом, эта модель определяется общим свободным членом (b0) и угловым коэффициентом, соответствующим b1 (если выражение x 500 истинно, т.е., равно 1) или b2 (если выражение x > 500 истинно, т.е., равно 1).

Вместо явного задания точки разрыва регрессионной кривой (500 единиц в месяц в последнем примере), можно также оценить положение этой точки. Например, мы могли заметить и предположить, что кривая себестоимости имеет разрыв в некоторой точке; однако не всегда очевидно, в какой именно точке происходит разрыв. В этом случае, достаточно просто заменить 500 в выписанном выше уравнении на дополнительный параметр (например, b3).

Регрессия с точками разрыва. Выписанное выше уравнение можно легко преобразовать к регрессии с точками разрыва, т.е. добавить скачкообразные изменения в некоторых точках кривой. Например, предположим, что после запуска устаревших станков, себестоимость “подпрыгнула” до более высокого уровня и затем продолжила медленно уменьшаться при увеличении объема производства. В этом случае, достаточно просто добавить (b3), тогда:

y = (b0 + b1*x)*(x 500) + (b3 + b2*x)*(x > 500)

Сравнение групп. Описанный здесь метод для оценивания различных регрессионных уравнений в разных областях значений независимых переменных может также быть использован для распознавания принадлежности элементов различным группам. Например, пусть в рассмотренном выше примере имеется три различных завода. Для простоты изложения “забудем” пока про возможные точки разрыва. Если сгруппировать переменные по принадлежности к соответствующему заводу, присвоив группирующей переменной значения 1,2 и 3, соответственно, мы сможем одновременно записать три различных регрессионных уравнения:

y = (xp=1)*(b10 + b11*x) + (xp=2)*(b20 + b21*x) + (xp=3)*(b30 + b31*x)



В этом уравнении, xp обозначает группирующую переменную, содержащую коды, определяющие завод, b10, b20 и b30 соответствуют свободным членам, а b11, b21 и b31 определяют угловые коэффициенты графика себестоимости (коэффициенты регрессии) для каждого завода. Вы можете сравнить правдоподобие этой и обычной регрессионной модели (без рассмотрения различных заводов) для того, чтобы определить более подходящую.

В начало

  Методы нелинейного оценивания Метод наименьших квадратов Функция потерь Метод взвешенных наименьших квадратов Метод максимума правдоподобия Максимум правдоподобия и логит/пробит модели Алгоритмы минимизации функций Начальные значения, размеры шагов и критерий сходимости Штрафные функции, ограничение параметров Локальные минимумы Квази-ньютоновский метод Симплекс-метод Метод Хука-Дживиса Метод Розенброка Матрица Гессе и стандартные ошибки
Методы нелинейного оценивания Метод наименьших квадратов Функция потерь Метод взвешенных наименьших квадратов Метод максимума правдоподобия Максимум правдоподобия и логит/пробит модели Алгоритмы минимизации функций Начальные значения, размеры шагов и критерий сходимости Штрафные функции, ограничение параметров Локальные минимумы Квази-ньютоновский метод Симплекс-метод Метод Хука-Дживиса Метод Розенброка Матрица Гессе и стандартные ошибки  

Метод наименьших квадратов.
Метод наименьших квадратов.

Некоторые более общие типы регрессионных моделей рассмотрены в разделе Основные типы нелинейных моделей. После выбора модели возникает вопрос: каким образом можно оценить эти модели? Если вы знакомы с методами линейной регрессии (описанными в разделе Множественная регрессия) или дисперсионного анализа (описанными в разделе Дисперсионный анализ), то вы знаете, что все эти методы используют оценивание по методу наименьших квадратов. Основной смысл этого метода заключается в минимизации суммы квадратов отклонений наблюдаемых значений зависимой переменной от значений, предсказанных моделью. (Термин наименьшие квадраты впервые был использован в работе Лежандра - Legendre, 1805.)



Функция потерь.

Функция потерь.

В стандартной множественной регрессии оценивание коэффициентов регрессии происходит “подбором” коэффициентов, минимизирующих дисперсию остатков (сумму квадратов остатков). Любые отклонения наблюдаемых величин от предсказанных означают некоторые потери в точности предсказаний, например, из-за случайного шума (ошибок). Поэтому можно сказать, что цель метода наименьших квадратов заключается в минимизации функции потерь. В этом случае, функция потерь определяется как сумма квадратов отклонений от предсказанных значений (термин функция потерь был впервые использован в работе Вальда - Wald, 1939). Когда эта функция достигает минимума, вы получаете те же оценки для параметров (свободного члена, коэффициентов регрессии), как, если бы мы использовали Множественную регрессию. Полученные оценки называются оценками по методу наименьших квадратов. Продолжая в том же духе, можно рассмотреть другие функции потерь. Например, при минимизации функции потерь, почему бы вместо суммы квадратов отклонений не рассмотреть сумму модулей отклонений? В самом деле, иногда это бывает полезно для уменьшения влияния выбросов. Влияние, оказываемое крупными остатками на всю сумму, существенно увеличивается при их возведении в квадрат. Однако если вместо суммы квадратов взять сумму модулей выбросов, влияние остатков на результирующую регрессионную кривую существенно уменьшится. Существуют несколько методов, которые могут быть использованы для минимизации различных видов функций потерь. Для получения дополнительной информации смотрите: Метод наименьших квадратов Функция потерь Метод взвешенных наименьших квадратов Метод максимума правдоподобия Максимум правдоподобия и логит/пробит модели Алгоритмы минимизации функций Начальные значения, размеры шагов и критерий сходимости Штрафные функции, ограничение параметров Локальные минимумы Квази-ньютоновский метод Симплекс-метод Метод Хука-Дживиса Метод Розенброка Матрица Гессе и стандартные ошибки Метод взвешенных наименьших квадратов.


Метод взвешенных наименьших квадратов.

Третьим по распространенности методом, в дополнение к методу наименьших квадратов и использованию для оценивания суммы модулей отклонений (см. выше), является метод взвешенных наименьших квадратов. Обычный метод наименьших квадратов предполагает, что разброс остатков одинаковый при всех значениях независимых переменных. Иными словами, предполагается, что дисперсия ошибки при всех измерениях одинакова. Часто, это предположение не является реалистичным. В частности, отклонения от него встречаются в бизнесе, экономике, приложениях в биологии (отметим, что оценки параметров по методу взвешенных наименьших квадратов могут быть также получены с помощью модуля Множественная регрессия).

Например, вы хотите изучить связь между проектной стоимостью постройки здания и суммой реально потраченных средств. Это может оказаться полезным для получения оценки ожидаемых перерасходов. В этом случае разумно предположить, что абсолютная величина перерасходов (выраженная в долларах) пропорциональна стоимости проекта. Поэтому, для подбора линейной регрессионной модели следует использовать метод взвешенных наименьших квадратов. Функция потерь может быть, например, такой (см. книгу Neter, Wasserman, and Kutner, 1985, стр.168):

Потери = (наблюд.-предск.)2 * (1/x2)

В этом уравнении первая часть функции потерь означает стандартную функцию потерь для метода наименьших квадратов (наблюдаемые минус предсказанные в квадрате; т.е., квадрат остатков), а вторая равна “весу” этой потери в каждом конкретном случае - единица деленная на квадрат независимой переменной (x) для каждого наблюдения. В ситуации реального оценивания, программа просуммирует значения функции потерь по всем наблюдениям (например, конструкторским проектам), как описано выше и подберет параметры, минимизирующие сумму. Возвращаясь к рассмотренному примеру, чем больше проект (x), тем меньше для нас значит одна и та же ошибка в предсказании его стоимости. Этот метод дает более устойчивые оценки для параметров регрессии (более подробно, см.


Neter, Wasserman, and Kutner, 1985).

Метод максимума правдоподобия.

Метод максимума правдоподобия.

Альтернативой использования метода наименьших квадратов (см выше) является поиск максимума функции правдоподобия или ее логарифма. Эквивалентным способом является минимизация логарифма функции правдоподобия со знаком минус (термин максимум правдоподобия впервые был использован в работе Фишера - Fisher, 1922a). В общем виде, функцию правдоподобия определяется так: L = F(Y,Модель) = in= 1 {p [yi, Параметры модели(xi)]}

Теоретически, вы можете вычислить вероятность принятия зависимой переменной определенных значений(обозначенную нами L, от слова Likelihood - правдоподобие), используя соответствующую регрессионную модель. Воспользовавшись тем, что все наблюдения независимы друг от друга, получим, что наша функция правдоподобия равна геометрической сумме (, для всех i = 1 to n) вероятностей конкретных наблюдений (i), заданных соответствующей значению x моделью и параметрами. (Геометрическая сумма означает, что нужно перемножить вероятности по всем возможным случаям внутри скобок.) Часто эти функции представляют в виде натурального логарифма, в этом случае геометрическая сумма становится обычной арифметической суммой (, для всех i = 1 to n).

При выборе конкретной модели, чем больше правдоподобие модели, тем больше вероятность, что предсказанное значение зависимой переменной окажется в выборке. Поэтому, чем больше правдоподобие, тем лучше модель согласуется с выборочными данными. Реальные вычисления для конкретной модели могут оказаться достаточно громоздкими, поскольку вам необходимо “отслеживать” (вычислять) вероятности появления различных значений зависимой переменной y (выбрав модель и соответствующее значение x). Оказывается, что если все предположения для стандартной множественной регрессии выполнены (они описаны в главе Множественная регрессия руководства пользователя), то стандартный метод наименьших квадратов (см. выше) дает те же оценки, что и метод максимума правдоподобия.


Если предположение о постоянстве дисперсии ошибки при всех значения независимой переменной нарушено, то оценки по методу максимума правдоподобия можно получить используя метод взвешенных наименьших квадратов.

Максимум правдоподобия и пробит/логит модели.

Максимум правдоподобия и пробит/логит модели.

Рассмотрим функцию правдоподобия для регрессионных моделей логит и пробит. Функция потерь для этих моделей вычисляется как сумма натуральных логарифмов логит или пробит правдоподобия L1: log(L1) = in= 1 [yi*log(pi ) + (1-yi )*log(1-pi )]

где
log(L1) натуральный логарифм функции правдоподобия для выбранной (логит или пробит) модели
yi - i-ое наблюдаемое значение
pi вероятность появления (предсказанная или подогнанная) (между 0 и 1)

Логарифм функции правдоподобия для нулевой модели (L0), т.е. модели, содержащей только свободный член (и не включающей других коэффициентов регрессии) вычисляется как:

log(L0) = n0*(log(n0/n)) + n1*(log(n1/n))

где
log(L0) натуральный логарифм функции правдоподобия для нулевой (логит или пробит) модели
n0 число наблюдений со значением 0
n1 число наблюдений со значением 1
n  общее число наблюдений

Алгоритмы минимизации функций

Алгоритмы минимизации функций

. Теперь, после обсуждения различных регрессионных моделей и функций потерь, используемых для их оценки, единственное, что осталось “в тайне”, это как находить минимумы функций потерь (т.е. наборы параметров, наилучшим образом соответствующие оцениваемой модели), и как вычислять стандартные ошибки оценивания параметров. Нелинейное оценивание использует очень эффективный (квази-ньютоновский) алгоритм, который приближенно вычисляет вторую производную функции потерь и использует ее при поиске минимума (т.е., при оценке параметров по соответствующей функции потерь). Кроме того, Нелинейное оценивание предлагает несколько более общих алгоритмов поиска минимума, использующих различные стратегии поиска (не связанные с вычислением вторых производных). Эти стратегии иногда более эффективны при оценивании функций потерь с локальными минимумами; поэтому, эти методы часто очень полезны для нахождения начальных значений с помощью квази-ньютоновского метода. Во всех случаях, вы можете вычислить стандартные ошибки оценок параметров.


Эти вычисления проводятся с использованием частных производных второго порядка по параметрам, которые приближенно подсчитываются с использованием метода конечных разностей.

Если вас интересует, не как именно происходит минимизация функции потерь, а только то, что такая минимизация в принципе возможна, вы можете пропустить следующие разделы. Однако они могут пригодиться, если получаемая регрессионная модель будет плохо согласовываться с данными. В этом случае, итеративная процедура может не сойтись, выдавая неожиданные (например, очень большие или очень маленькие) оценки для параметров.

В следующих параграфах, мы сначала рассмотрим некоторые вопросы, относящиеся к оптимизации без ограничений, затем дадим краткий обзор методов используемых в этом модуле. Более подробное обсуждение этих методов имеется в книгах Brent (1973), Gill and Murray (1974), Peressini, Sullivan, and Uhl (1988), и Wilde and Beightler (1967). Более широкий обзор алгоритмов можно найти в книгах Dennis and Schnabel (1983), Eason and Fenton (1974), Fletcher (1969), Fletcher and Powell (1963), Fletcher and Reeves (1964), Hooke and Jeeves (1961), Jacoby, Kowalik, and Pizzo (1972), и Nelder and Mead (1964).

Начальные значения, размеры шагов и критерии сходимости

Начальные значения, размеры шагов и критерии сходимости

. Общим моментом всех методов оценивания является необходимость задания пользователем некоторых начальных значений, размера шагов и критерия сходимости алгоритма. Все методы начинают свою работу с особого набора предварительных оценок (начальных значений), которые в дальнейшем последовательно уточняются от итерации к итерации. При первой итерации размер шага определяет, как сильно будут меняться параметры. Наконец, критерий сходимости определяет, когда итерационный процесс можно прекратить. Например, процесс итераций можно остановить, когда изменение функции потерь на каждом шаге становится меньше определенной величины.

Штрафные функции, ограничение параметров. Все процедуры Нелинейного оценивания не имеют встроенных ограничений на область поиска.


Это означает, что программа будет изменять значения параметров вне зависимости от допустимости получаемых значений. Например, в ходе логит регрессии оцениваемое значение можете получиться равным 0.0. В этом случае мы не можем вычислить логарифм (поскольку логарифм нуля не определен). В этой ситуации программа автоматически присваивает функции потерь штрафное значение, т.е. очень большое значение. В результате, оценивающие процедуры остаются внутри допустимого диапазона. Однако, в некоторых случаях, процесс оценивания зацикливается, и в результате, мы получаем огромное значение функции потерь. Это может случиться, например, если, если регрессионное уравнение включает взятие логарифма от независимой переменной, которая в некоторых случаях может принимать нулевое значение (в этом случае возникают проблемы с логарифмированием). Для того, чтобы определить ограничения на область изменения параметров, следует добавить к функции потерь некоторую штрафную функцию, равную нулю при допустимых значениях параметра и очень большую при недопустимых. Ниже приведен пример определенной пользователем регрессии и функции потерь, включающий наложение штрафа, если хотя бы один из параметров a или b меньше или равен нуля:

Оцениваемая функция: v3 = a + b*v1 + (c*v2)
Функция потерь: L = (obs - pred)**2 + (a<0)*100000 + (b<0)*100000

Локальные минимумы.

Локальные минимумы.

Самой неприятной проблемой при минимизации функции без ограничений являются локальные минимумы. Например, при небольшом смещении значения параметра в любом направлении функция потерь почти не изменяется. Однако если мы передвинем параметр в совершенно другую область, значение функции потерь может существенно уменьшиться. Вы можете представлять себе такие локальные минимумы как небольшие впадины на графике функции потерь. Однако в большинстве практических приложений локальные минимумы приводят к неправдоподобно большим или неправдоподобно малым значениям параметров с очень большими стандартными ошибками. В этих случаях следует задать другие начальные данные и повторить поиск минимума еще раз.


Отметим также, что симплекс - метод (см. ниже) нечувствителен к таким минимумам, поэтому, он может быть использован для отыскания подходящих начальных значений для сложных функций.

Квази-ньютоновский метод. Как вы, наверное, помните, угловой коэффициент - тангенс угла наклона графика функции в конкретной точке равен производной этой функции (в этой точке), а скорость его изменения в выбранной точке равна второй производной функции в этой точке. Квази-ньютоновский метод вычисляет значения функции в различных точках для оценивания первой и второй производной, используя эти данные для определения направления изменения параметров и минимизации функции потерь.

Симплекс-метод. Этот алгоритм не использует производные функции потерь. Вместо этого, при каждой итерации функция оценивается в m+1 точках m-мерного пространства. Например, на плоскости (т.е., при оценивании двух параметров) программа будет вычислять значение функции потерь в трех точках в окрестности текущего минимума. Эти три точки определяют треугольник; в многомерном пространстве. Получаемая фигура называется симплекс. Интуитивно понятно, что в двумерном пространстве три точки позволяют выбрать “в каком направлении двигаться”, т.е., в каком направлении на плоскости менять параметры для минимизации функции. Похожие принципы применимы в многомерном параметрическом пространстве; т.е., симплекс будет постепенно “смещаться вниз по склону”, в сторону минимизации функции потерь; если же текущий шаг окажется слишком большим для определения точного направления спуска, (т.е., симплекс слишком большой), процедура произведет уменьшение симплекса и продолжит вычисления. Дополнительное преимущество симплекс-метода в том, что при нахождении минимума симплекс снова увеличивается для проверки: не является ли этот минимум локальным. Таким образом, симплекс движется по поверхности по направлению к минимуму функции подобно простому, одноклеточному, организму, уменьшаясь и увеличиваясь при обнаружении локальных минимумов и “гребней”.



Метод Хука-Дживиса.

Метод Хука-Дживиса.

В некотором смысле, это простейший из всех алгоритмов. При каждой итерации метод сначала определяет схему расположения параметров, оптимизируя текущую функцию потерь перемещением каждого параметра по отдельности. При этом вся комбинация параметров сдвигается на новое место. Это новое положение в m-мерном пространстве параметров определяется экстраполяцией вдоль линии, соединяющей текущую базовую точку с новой точкой. Размер шага этого процесса постоянно меняется для попадания в оптимальную точку. Этот метод обычно очень эффективен и его следует использовать, если квази-ньютоновский и симплекс-метод (см. выше) не дали удовлетворительных оценок.

Метод Розенброка. Даже если все остальные методы не сработали, метод Розенброка часто приводит к правильному результату. Этот метод вращает пространство параметров, располагая одну ось вдоль “гребня” поверхности (этот метод также называется метод вращения координат), при этом все другие остаются ортогональными выбранной оси. Если поверхность графика функции потерь имеет одну вершину и различимые “гребни” в направлении минимума функции потерь, этот метод приводит к очень точным значениям параметров, минимизирующим функцию потерь. Однако следует отметить, что этот поисковый алгоритм остановится преждевременно, если на область значений параметров наложены несколько ограничений (отражающихся в штрафном значении; см. выше), которые пересекаются, приводя к обрыванию “гребня”.

Матрица Гессе и стандартные ошибки. Матрицу частных производных второго порядка также часто называют матрицей Гессе. Оказывается, что обратная к ней матрица приблизительно равна матрице ковариаций оцениваемых параметров. Интуитивно понятно, что существует обратная зависимость между производными второго порядка по параметрам и их стандартными ошибками. Если изменить угловой коэффициент в точке минимума функции и сделать минимум функции более “резким”, то производные второго порядка увеличатся; при этом, оценки параметров будут практически стабильными в смысле, что параметры в точке минимума будут легко уточняемы.


Если же производная второго порядка будет близка к нулю, то угол наклона в точке минимума будет практически неизменным, приводя к тому, что вы можете двигать параметры практически в любом направлении почти не изменяя значение функции потерь. Поэтому стандартные ошибки параметров будут очень большими. Матрица Гессе и асимптотические стандартные ошибки для параметров вычисляются отдельно методом конечных разностей. Эта процедура возвращает очень точные асимптотические стандартные ошибки для всех методов оценивания.

В начало

Оценивание пригодности модели
Оценивание пригодности модели

После оценивания регрессионных параметров, существенной стороной анализа является проверка пригодности модели в целом. Например, если вы определили линейную регрессионную модель, а реальная зависимость переменных по своей природе нелинейна, то оценки параметров (коэффициентов регрессии) и оценки стандартных ошибок этих приближений могут оказаться совершенно неудовлетворительными. Рассмотрим некоторые методы проверки пригодности модели. Объясненная доля дисперсии Критерий согласия хи-квадрат График наблюдаемых и предсказанных значений Нормальный и полунормальный график остатков График функции подгонки Ковариационная матрица оценок параметров  


Объясненная доля дисперсии.
Объясненная доля дисперсии.

Вне зависимости от рассматриваемой модели, мы всегда можем оценить полную дисперсию зависимой переменной (полную сумму квадратов - total sum of squares, SST), долю дисперсии, приходящейся на остатки (сумму квадратов ошибок - error sum of squares, SSE), и долю дисперсии относительно регрессионной модели (сумму квадратов относительно регрессии - regression sum of squares, SSR = SST - SSE). Отношение суммы квадратов относительно регрессии к полной сумме квадратов (SSR/SST) обозначается термином объясненная доля дисперсии зависимой переменной (y) в регрессионной модели. Таким образом, эта доля эквивалентна значению R-квадрат (0 R-квадрат 1, так называемому квадрату смешанной корреляции (коэффициенту определенности- coefficient of determination в англоязычной литературе)).


Даже если распределение зависимой переменной не является нормальным, это отношение помогает оценить, насколько хорошо подобранная модель согласуется с исходными данными.

Критерий согласия хи-квадрат.

Критерий согласия хи-квадрат.

Для регрессионных моделей пробит и логит, Нелинейное оценивание использует оценивание по методу максимума правдоподобия (т.е. максимизирует функцию правдоподобия). Но оказывается, что можно непосредственно сравнить правдоподобие L0 нулевой модели, где все параметры наклона равны нулю, с правдоподобием L1 подогнанной модели. А именно, можно вычислить значение статистики хи-квадрат для нашего отношения по формуле: Хи-квадрат = -2 * (log(L0) - log(L1))

Число степеней свободы для этого значения хи-квадрат равно разности числа параметров для подогнанной и числа параметров для нулевой моделей, поэтому число степеней свободы будет равно числу независимых переменных в подогнанной логит или пробит регрессии. Если p-уровень, соответствующий этому значению хи-квадрат, является значимым, то вы можете сказать, что оцениваемая модель значительно лучше соответствует данным, чем нулевая модель, т.е. параметры регрессии статистически значимы.

График наблюдаемых и предсказанных значений.

График наблюдаемых и предсказанных значений.

При проведении исследований часто полезным бывает использование диаграммы рассеяния наблюдаемых и предсказанных значений. Если модель хорошо соответствует данным, можно ожидать, что точки расположатся вдоль прямой линии, если же модель задана неправильно, то полученная из точек на графике фигура будет мало похожа на прямую линию.

Нормальный и полунормальный графики остатков. Нормальный вероятностный график остатков показывает насколько распределение остатков (ошибок) близко к нормальному.

График функции подгонки. Для моделей, включающих две или три переменные (один или два предиктора) полезно строить функцию подгонки с использованием окончательных оценок параметров. Посмотрите на пример 3М графика с двумя предикторными переменными:



Этот тип графика предоставляет хорошую возможность проверить, подходит ли модель к данным или нет, и где расположены явные выбросы.

Ковариационная матрица оценок параметров.

Ковариационная матрица оценок параметров.

Если подобранная модель сильно отличается от реальной, или процедура оценивания “застряла” на локальном минимуме, ошибки для оценок параметров могут получиться очень большими. Это означает, что как бы мы не меняли конечные значения параметров, полученная в результате функция потерь практически не изменится. Кроме того, параметры могут оказаться сильно коррелированными. Это говорит о том, что некоторые параметры излишни. Поэтому изменение функции потерь при изменении оценивающим алгоритмом полученного значения одного параметра может быть практически скомпенсировано перемещением другого параметра и изучение совместного влияния этих параметров на функцию потерь оказывается излишним.

В начало

(c) Copyright StatSoft, Inc., 1984-2001
STATISTICA является торговой маркой StatSoft, Inc.

Непараметрическая статистика и подгонка распределения

Непараметрическая статистика и подгонка распределения

Основная цель Краткий обзор непараметрических процедур Какой метод использовать Подгонка распределения

Основная цель Краткий обзор непараметрических процедур Какой метод использовать Подгонка распределения

Основная цель

Основная цель

Краткий обзор понятия "критерий значимости".
Краткий обзор понятия "критерий значимости".

Для того чтобы понять идеи непараметрической статистики (термин был впервые введен Wolfowitz, 1942), следует познакомиться с идеями параметрической статистики. Глава Элементарные понятия статистики знакомит с понятием статистической значимости критерия, основанного на выборочном распределении определенной статистики (вы можете просмотреть эту главу, прежде чем продолжить чтение). Говоря кратко, если вы знаете распределение наблюдаемой переменной, то можете предсказать, как в повторных выборках равного объема будет "вести себя" используемая статистика - т.е. каким образом она будет распределена. Пусть, например, имеется 100 случайных выборок, из одной популяции по 100 взрослых человек в каждой. Вычислим средний рост субъектов в каждой выборке, т.е. построим выборочное среднее. Тогда распределение выборочных средних можно хорошо аппроксимировать нормальным распределением (более точно, t распределением Стьюдента с 99 степенями свободы). Теперь представьте, что случайным образом извлечена еще одна выборка из жителей некоего города ("Вышгород"), где, по вашим представлениям, проживают люди с ростом выше среднего. Если средний рост людей в этой выборке попадает в верхнюю 95% критическую область tраспределения, то можно сделать обоснованный вывод, что жители Вышгорода, действительно, в среднем более высокие (чем в целом в популяции), т.е. что это действительно город высоких людей.

Действительно ли большинство переменных имеют нормальное распределение?
Действительно ли большинство переменных имеют нормальное распределение?

В рассмотренном примере использовался тот факт, что в повторных выборках равного объемы средние значения (роста людей) будут иметь t распределение (с определенным средним и дисперсией).
Однако, это верно лишь, если рассматриваемая переменная (рост) имеет нормальное распределение, т.е. что распределение людей определенного роста нормально распределено.



Для многих изучаемых переменных невозможно сказать с уверенностью, что это действительно так. Например, является ли доход нормально распределенной величиной? - скорее всего, нет. Случаи редких болезней не являются нормально распределенными в популяции, число автомобильных аварий также не является нормально распределенным, как и многие переменные, интересующие исследователя.

Дополнительную информацию о нормальном распределении можно посмотреть в разделе Элементарные понятия статистики.

Объем выборки.
Объем выборки.

Другим фактором, часто ограничивающим применимость критериев, основанных на предположении нормальности, является объем или размер выборки, доступной для анализа. До тех пор пока выборка достаточно большая (например, 100 или больше наблюдений), можно считать, что выборочное распределение нормально, даже если вы не уверены, что распределение переменной в популяции, действительно, является нормальным. Тем не менее, если выборка очень мала, то критерии, основанные на нормальности, следует использовать только при наличии уверенности, что переменная действительно имеет нормальное распределение. Однако нет способа проверить это предположение на малой выборке.

Проблемы измерения.
Проблемы измерения.

Использование критериев, основанных на предположении нормальности, кроме того, ограничено точностью измерений. Например, рассмотрим исследование, в котором средний балл успеваемости (СБУ) является основной переменной. Можно ли сказать, что средняя успеваемость студента A в два раза выше, чем успеваемость студента C? Является ли различие между средним баллом студентов B и A сравнимым с различием между студентами D и C? Индекс СБУ является грубой мерой, позволяющей только ранжировать студентов в порядке "хороший" - "плохой". Эта общая задача измерений обычно обсуждается в учебниках по статистике в терминах типов измерений или шкалы измерения.


Не вдаваясь в детали, отметим, что наиболее общие статистические методы, такие как дисперсионный анализ (t-критерий), регрессия и т.д. предполагают, что исходные измерения выполнены, по крайней мере, в интервальной шкале, в которой интервалы можно разумным образом сравнивать между собой (например, B минус A равняется D минус C). Тем не менее, как в данном примере, такие предположения часто неестественны, и данные скорее просто упорядочены (измерены в порядковой шкале), чем измерены точно.

Параметрические и непараметрические методы.
Параметрические и непараметрические методы.

Надеемся, что после этого введения становится ясной необходимость наличия статистических процедур, позволяющих обрабатывать данные "низкого качества" из выборок малого объема с переменными, про распределение которых мало что или вообще ничего не известно. Непараметрические методы как раз и разработаны для тех ситуаций, достаточно часто возникающих на практике, когда исследователь ничего не знает о параметрах исследуемой популяции (отсюда и название методов - непараметрические). Говоря более специальным языком, непараметрические методы не основываются на оценке параметров (таких как среднее или стандартное отклонение) при описании выборочного распределения интересующей величины. Поэтому эти методы иногда также называются свободными от параметров или свободно распределенными.

В начало

Краткий обзор непараметрических процедур

Краткий обзор непараметрических процедур

По существу, для каждого параметрического критерия имеется, по крайней мере, один непараметрический аналог. Эти критерии можно отнести к одной из следующих групп: критерии различия между группами (независимые выборки); критерии различия между группами (зависимые выборки); критерии зависимости между переменными. Различия между независимыми группами. Обычно, когда имеются две выборки (например, мужчины и женщины), которые вы хотите сравнить относительно среднего значения некоторой изучаемой переменной, вы используете t-критерий для независимых выборок (в модуле Основные статистики и таблицы).


Непараметрическими альтернативами этому критерию являются: критерий серий Вальда-Вольфовица, U критерий Манна-Уитни и двухвыборочный критерий Колмогорова-Смирнова. Если вы имеете несколько групп, то можете использовать дисперсионный анализ (см. Дисперсионный анализ). Его непараметрическими аналогами являются: ранговый дисперсионный анализ Краскела-Уоллиса и медианный тест. Различия между зависимыми группами.
Различия между зависимыми группами.

Если вы хотите сравнить две переменные, относящиеся к одной и той же выборке (например, математические успехи студентов в начале и в конце семестра), то обычно используется t-критерий для зависимых выборок (в модуле Основные статистики и таблицы. Альтернативными непараметрическими тестами являются: критерий знаков и критерий Вилкоксона парных сравнений. Если рассматриваемые переменные по природе своей категориальны или являются категоризованными (т.е. представлены в виде частот попавших в определенные категории), то подходящим будет критерий хи-квадрат Макнемара. Если рассматривается более двух переменных, относящихся к одной и той же выборке, то обычно используется дисперсионный анализ (ANOVA) с повторными измерениями. Альтернативным непараметрическим методом является ранговый дисперсионный анализ Фридмана или Q критерий Кохрена (последний применяется, например, если переменная измерена в номинальной шкале). Q критерий Кохрена используется также для оценки изменений частот (долей).

Зависимости между переменными.
Зависимости между переменными.

Для того, чтобы оценить зависимость (связь) между двумя переменными, обычно вычисляют коэффициент корреляции. Непараметрическими аналогами стандартного коэффициента корреляции Пирсона являются статистики Спирмена R, тау Кендалла и коэффициент Гамма (см. Непараметрические корреляции). Если две рассматриваемые переменные по природе своей категориальны, подходящими непараметрическими критериями для тестирования зависимости будут: Хи-квадрат, Фи коэффициент, точный критерий Фишера. Дополнительно доступен критерий зависимости между несколькими переменными так называемый коэффициент конкордации Кендалла.


Этот тест часто используется для оценки согласованности мнений независимых экспертов (судей), в частности, баллов, выставленных одному и тому же субъекту.

Описательные статистики.
Описательные статистики.

Если данные не являются нормально распределенными, а измерения, в лучшем случае, содержат ранжированную информацию, то вычисление обычных описательных статистик (например, среднего, стандартного отклонения) не слишком информативно. Например, в психометрии хорошо известно, что воспринимаемая интенсивность стимулов (например, воспринимаемая яркость света) представляет собой логарифмическую функцию реальной интенсивности (яркости, измеренной в объективных единицах - люксах). В данном примере, обычная оценка среднего (сумма значений, деленная на число стимулов) не дает верного представления о среднем значении действительной интенсивности стимула. (В обсуждаемом примере скорее следует вычислить геометрическое среднее.) Модуль Непараметрическая статистика вычисляет разнообразный набор мер положения (среднее, медиану, моду и т.д.) и рассеяния (дисперсию, гармоническое среднее, квартильный размах и т.д.), позволяющий представить более "полную картину" данных.

В начало

Какой метод использовать
Какой метод использовать

Нелегко дать простой совет, касающийся использования непараметрических процедур. Каждая непараметрическая процедура в модуле имеет свои достоинства и свои недостатки. Например, двухвыборочный критерий Колмогорова-Смирнова чувствителен не только к различию в положении двух распределений, например, к различиям средних, но также чувствителен и к форме распределения. Критерий Вилкоксона парных сравнений предполагает, что можно ранжировать различия между сравниваемыми наблюдениями. Если это не так, лучше использовать критерий знаков. В общем, если результат исследования является важным (например, оказывает ли людям помощь определенная очень дорогостоящая и болезненная терапия?), то всегда целесообразно применить различные непараметрические тесты.


Возможно, результаты проверки (разными тестами) будут различны. В таком случае следует попытаться понять, почему разные тесты дали разные результаты. С другой стороны, непараметрические тесты имеют меньшую статистическую мощность (менее чувствительны), чем их параметрические конкуренты, и если важно обнаружить даже слабые отклонения (например, является ли данная пищевая добавка опасной для людей), следует особенно внимательно выбирать статистику критерия.

Большие массивы данных и непараметрические методы.
Большие массивы данных и непараметрические методы.

Непараметрические методы наиболее приемлемы, когда объем выборок мал. Если данных много (например, n > 100), то не имеет смысла использовать непараметрические статистики. Глава Элементарные понятия статистики предлагает краткое ознакомление с центральной предельной теоремой. Главное здесь состоит в том, что когда выборки становятся очень большими, то выборочные средние подчиняются нормальному закону, даже если исходная переменная не является нормальной или измерена с погрешностью. Таким образом, параметрические методы, являющиеся более чувствительными (имеют большую статистическую мощность), всегда подходят для больших выборок. Большинство критериев значимости многих непараметрических статистик, описанных далее, основываются на асимптотической теории (больших выборок) поэтому соответствующие тесты часто не выполняются, если размер выборки становится слишком малым. Обратитесь к описаниям определенных критериев, чтобы узнать больше об их мощности и эффективности.

Подгонка распределения
Подгонка распределения

В некоторых исследовательских проектах можно сформулировать гипотезы относительно распределения рассматриваемой переменной. Например, переменные, значения которых определяются бесконечным числом независимых факторов, распределены по нормальному закону: можно предположить, что рост индивидуума является результатом воздействия многих независимых факторов, таких как различные генетические предрасположенности, болезни, перенесенные в раннем возрасте и т.д.


Как следствие, рост имеет тенденцию к нормальному распределению в населении. С другой стороны, если наблюдаемые значения переменной являются результатом очень редких событий, то переменная будет иметь распределение Пуассона (которое иногда называется распределением редких событий). Например, несчастные случаи на производстве можно рассматривать как результат пересечения ряда неудачных событий (на житейском языке стечением маловероятных обстоятельств), поэтому их частота приближенно описывается распределением Пуассона. Эти и другие полезные распределения подробно описываются в соответствующих разделах.

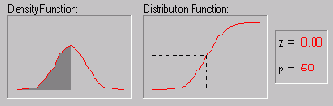
Гипотеза нормальности.
Гипотеза нормальности.

Другим обычным приложением процедуры подгонки распределения является проверка гипотезы нормальности до того, как использовать какой-либо параметрический тест (см. выше).

В начало

(c) Copyright StatSoft, Inc., 1984-2001
STATISTICA является торговой маркой StatSoft, Inc.

Основные статистики и таблицы

Основные статистики и таблицы

Описательные статистики "Истинное" среднее и доверительный интервал Форма распределения; нормальность Корреляции Определение корреляции Простая линейная корреляция (Пирсона r) Как интерпретировать значения корреляций Значимость корреляций Выбросы Количественный подход к выбросам Корреляции в неоднородных группах Нелинейные зависимости между переменными Измерение нелинейных зависимостей Разведочный анализ корреляционных матриц Построчное удаление пропущенных данных в сравнении с попарным удалением Как определить смещения, вызванные попарным удалением пропущенных данных Попарное удаление пропущенных данных в сравнении с подстановкой среднего значения Ложные корреляции Являются ли коэффициенты корреляции "аддитивными"? Как определить, являются ли два коэффициента корреляции значимо различными t-критерий для независимых выборок Цель, предположения Расположение данных Графики t-критериев Более сложные групповые сравнения t-критерий для зависимых выборок Внутригрупповая вариация Цель Предположения Расположение данных Матрицы t-критериев Более сложные групповые сравнения Внутригрупповые описательные статистики и корреляции (группировка) Цель Расположение данных Статистические тесты для группированных данных Другие близкие методы анализа данных Апостериорные сравнения средних Группировка в сравнении с дискриминантным анализом Группировка в сравнении c таблицами частот Графическое представление группировки Таблицы частот Цель Приложения Таблицы сопряженности и таблицы флагов и заголовков Цель и расположение данных Таблицы 2x2 Маргинальные частоты Проценты по столбцам, по строкам и проценты от общего числа наблюдений Графическое представление таблиц сопряженности Таблицы флагов и заголовков Интерпретация таблиц заголовков Многовходовые таблицы с категориальными переменными Графическое представление многовходовых таблиц Статистики таблиц сопряженности Многомерные отклики и дихотомии

Описательные статистики "Истинное" среднее и доверительный интервал Форма распределения; нормальность Корреляции Определение корреляции Простая линейная корреляция (Пирсона r) Как интерпретировать значения корреляций Значимость корреляций Выбросы Количественный подход к выбросам Корреляции в неоднородных группах Нелинейные зависимости между переменными Измерение нелинейных зависимостей Разведочный анализ корреляционных матриц Построчное удаление пропущенных данных в сравнении с попарным удалением Как определить смещения, вызванные попарным удалением пропущенных данных Попарное удаление пропущенных данных в сравнении с подстановкой среднего значения Ложные корреляции Являются ли коэффициенты корреляции "аддитивными"? Как определить, являются ли два коэффициента корреляции значимо различными t-критерий для независимых выборок Цель, предположения Расположение данных Графики t-критериев Более сложные групповые сравнения t-критерий для зависимых выборок Внутригрупповая вариация Цель Предположения Расположение данных Матрицы t-критериев Более сложные групповые сравнения Внутригрупповые описательные статистики и корреляции (группировка) Цель Расположение данных Статистические тесты для группированных данных Другие близкие методы анализа данных Апостериорные сравнения средних Группировка в сравнении с дискриминантным анализом Группировка в сравнении c таблицами частот Графическое представление группировки Таблицы частот Цель Приложения Таблицы сопряженности и таблицы флагов и заголовков Цель и расположение данных Таблицы 2x2 Маргинальные частоты Проценты по столбцам, по строкам и проценты от общего числа наблюдений Графическое представление таблиц сопряженности Таблицы флагов и заголовков Интерпретация таблиц заголовков Многовходовые таблицы с категориальными переменными Графическое представление многовходовых таблиц Статистики таблиц сопряженности Многомерные отклики и дихотомии

Описательные статистики



"Истинное" среднее и доверительный интервал. Вероятно, большинство из вас использовало такую важную описательную статистику, как среднее. Среднее - очень информативная мера "центрального положения" наблюдаемой переменной, особенно если сообщается ее доверительный интервал. Исследователю нужны такие статистики, которые позволяют сделать вывод относительно популяции в целом. Одной из таких статистик является среднее. Доверительный интервал для среднего представляет интервал значений вокруг оценки, где с данным уровнем доверия (см. Элементарные понятия статистики), находится "истинное" (неизвестное) среднее популяции. Например, если среднее выборки равно 23, а нижняя и верхняя границы доверительного интервала с уровнем p=.95 равны 19 и 27 соответственно, то можно заключить, что с вероятностью 95% интервал с границами 19 и 27 накрывает среднее популяции. Если вы установите больший уровень доверия, то интервал станет шире, поэтому возрастает вероятность, с которой он "накрывает" неизвестное среднее популяции, и наоборот. Хорошо известно, например, что чем "неопределенней" прогноз погоды (т.е. шире доверительный интервал), тем вероятнее он будет верным. Заметим, что ширина доверительного интервала зависит от объема или размера выборки, а также от разброса (изменчивости) данных. Увеличение размера выборки делает оценку среднего более надежной. Увеличение разброса наблюдаемых значений уменьшает надежность оценки (см. также Элементарные понятия статистики). Вычисление доверительных интервалов основывается на предположении нормальности наблюдаемых величин. Если это предположение не выполнено, то оценка может оказаться плохой, особенно для малых выборок. При увеличении объема выборки, скажем, до 100 или более, качество оценки улучшается и без предположения нормальности выборки.
"Истинное" среднее и доверительный интервал. Вероятно, большинство из вас использовало такую важную описательную статистику, как среднее. Среднее - очень информативная мера "центрального положения" наблюдаемой переменной, особенно если сообщается ее доверительный интервал.


Исследователю нужны такие статистики, которые позволяют сделать вывод относительно популяции в целом. Одной из таких статистик является среднее. Доверительный интервал для среднего представляет интервал значений вокруг оценки, где с данным уровнем доверия (см. Элементарные понятия статистики), находится "истинное" (неизвестное) среднее популяции. Например, если среднее выборки равно 23, а нижняя и верхняя границы доверительного интервала с уровнем p=.95 равны 19 и 27 соответственно, то можно заключить, что с вероятностью 95% интервал с границами 19 и 27 накрывает среднее популяции. Если вы установите больший уровень доверия, то интервал станет шире, поэтому возрастает вероятность, с которой он "накрывает" неизвестное среднее популяции, и наоборот. Хорошо известно, например, что чем "неопределенней" прогноз погоды (т.е. шире доверительный интервал), тем вероятнее он будет верным. Заметим, что ширина доверительного интервала зависит от объема или размера выборки, а также от разброса (изменчивости) данных. Увеличение размера выборки делает оценку среднего более надежной. Увеличение разброса наблюдаемых значений уменьшает надежность оценки (см. также Элементарные понятия статистики). Вычисление доверительных интервалов основывается на предположении нормальности наблюдаемых величин. Если это предположение не выполнено, то оценка может оказаться плохой, особенно для малых выборок. При увеличении объема выборки, скажем, до 100 или более, качество оценки улучшается и без предположения нормальности выборки.

Форма распределения; нормальность. Важным способом "описания" переменной является форма ее распределения, которая показывает, с какой частотой значения переменной попадают в определенные интервалы. Эти интервалы, называемые интервалами группировки, выбираются исследователем. Обычно исследователя интересует, насколько точно распределение можно аппроксимировать нормальным (см. ниже картинку с примером такого распределения) (см.


также Элементарные понятия статистики). Простые описательные статистики дают об этом некоторую информацию. Например, если асимметрия (показывающая отклонение распределения от симметричного) существенно отличается от 0, то распределение несимметрично, в то время как нормальное распределение абсолютно симметрично. Итак, у симметричного распределения асимметрия равна 0. Асимметрия распределения с длинным правым хвостом положительна. Если распределение имеет длинный левый хвост, то его асимметрия отрицательна. Далее, если эксцесс (показывающий "остроту пика" распределения) существенно отличен от 0, то распределение имеет или более закругленный пик, чем нормальное, или, напротив, имеет более острый пик (возможно, имеется несколько пиков). Обычно, если эксцесс положителен, то пик заострен, если отрицательный, то пик закруглен. Эксцесс нормального распределения равен 0.
Форма распределения; нормальность. Важным способом "описания" переменной является форма ее распределения, которая показывает, с какой частотой значения переменной попадают в определенные интервалы. Эти интервалы, называемые интервалами группировки, выбираются исследователем. Обычно исследователя интересует, насколько точно распределение можно аппроксимировать нормальным (см. ниже картинку с примером такого распределения) (см. также Элементарные понятия статистики). Простые описательные статистики дают об этом некоторую информацию. Например, если асимметрия (показывающая отклонение распределения от симметричного) существенно отличается от 0, то распределение несимметрично, в то время как нормальное распределение абсолютно симметрично. Итак, у симметричного распределения асимметрия равна 0. Асимметрия распределения с длинным правым хвостом положительна. Если распределение имеет длинный левый хвост, то его асимметрия отрицательна. Далее, если эксцесс (показывающий "остроту пика" распределения) существенно отличен от 0, то распределение имеет или более закругленный пик, чем нормальное, или, напротив, имеет более острый пик (возможно, имеется несколько пиков).


Обычно, если эксцесс положителен, то пик заострен, если отрицательный, то пик закруглен. Эксцесс нормального распределения равен 0.

Более точную информацию о форме распределения можно получить с помощью критериев нормальности (например, критерия Колмогорова-Смирнова или W критерия Шапиро-Уилка). Однако ни один из этих критериев не может заменить визуальную проверку с помощью гистограммы (графика, показывающего частоту попаданий значений переменной в отдельные интервалы).



Гистограмма позволяет "на глаз" оценить нормальность эмпирического распределения. На гистограмму также накладывается кривая нормального распределения. Гистограмма позволяет качественно оценить различные характеристики распределения. Например, на ней можно увидеть, что распределение бимодально (имеет 2 пика). Это может быть вызвано, например, тем, что выборка неоднородна, возможно, извлечена из двух разных популяций, каждая из которых более или менее нормальна. В таких ситуациях, чтобы понять природу наблюдаемых переменных, можно попытаться найти качественный способ разделения выборки на две части.

В начало

Корреляции

Определение корреляции. Корреляция представляет собой меру зависимости переменных. Наиболее известна корреляция Пирсона. При вычислении корреляции Пирсона предполагается, что переменные измерены, как минимум, в интервальной шкале. Некоторые другие коэффициенты корреляции могут быть вычислены для менее информативных шкал. Коэффициенты корреляции изменяются в пределах от -1.00 до +1.00. Обратите внимание на крайние значения коэффициента корреляции. Значение -1.00 означает, что переменные имеют строгую отрицательную корреляцию. Значение +1.00 означает, что переменные имеют строгую положительную корреляцию. Отметим, что значение 0.00 означает отсутствие корреляции.
Определение корреляции. Корреляция представляет собой меру зависимости переменных. Наиболее известна корреляция Пирсона. При вычислении корреляции Пирсона предполагается, что переменные измерены, как минимум, в интервальной шкале.


Некоторые другие коэффициенты корреляции могут быть вычислены для менее информативных шкал. Коэффициенты корреляции изменяются в пределах от -1.00 до +1.00. Обратите внимание на крайние значения коэффициента корреляции. Значение -1.00 означает, что переменные имеют строгую отрицательную корреляцию. Значение +1.00 означает, что переменные имеют строгую положительную корреляцию. Отметим, что значение 0.00 означает отсутствие корреляции.

Наиболее часто используемый коэффициент корреляции Пирсона r называется также линейной корреляцией, т.к. измеряет степень линейных связей между переменными.

Простая линейная корреляция (Пирсона r). Корреляция Пирсона (далее называемая просто корреляцией) предполагает, что две рассматриваемые переменные измерены, по крайней мере, в интервальной шкале (см. Элементарные понятия статистики). Она определяет степень, с которой значения двух переменных "пропорциональны" друг другу. Важно, что значение коэффициента корреляции не зависит от масштаба измерения. Например, корреляция между ростом и весом будет одной и той же, независимо от того, проводились измерения в дюймах и фунтах или в сантиметрах и килограммах. Пропорциональность означает просто линейную зависимость. Корреляция высокая, если на графике зависимость "можно представить" прямой линией (с положительным или отрицательным углом наклона).
Простая линейная корреляция (Пирсона r). Корреляция Пирсона (далее называемая просто корреляцией) предполагает, что две рассматриваемые переменные измерены, по крайней мере, в интервальной шкале (см. Элементарные понятия статистики). Она определяет степень, с которой значения двух переменных "пропорциональны" друг другу. Важно, что значение коэффициента корреляции не зависит от масштаба измерения. Например, корреляция между ростом и весом будет одной и той же, независимо от того, проводились измерения в дюймах и фунтах или в сантиметрах и килограммах. Пропорциональность означает просто линейную зависимость.


Корреляция высокая, если на графике зависимость "можно представить" прямой линией (с положительным или отрицательным углом наклона).

Проведенная прямая называется прямой регрессии или прямой, построенной методом наименьших квадратов. Последний термин связан с тем, что сумма квадратов расстояний (вычисленных по оси Y) от наблюдаемых точек до прямой является минимальной. Заметим, что использование квадратов расстояний приводит к тому, что оценки параметров прямой сильно реагируют на выбросы.

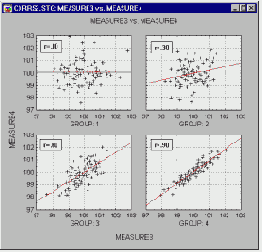
Как интерпретировать значения корреляций. Коэффициент корреляции Пирсона (r) представляет собой меру линейной зависимости двух переменных. Если возвести его в квадрат, то полученное значение коэффициента детерминации r2) представляет долю вариации, общую для двух переменных (иными словами, "степень" зависимости или связанности двух переменных). Чтобы оценить зависимость между переменными, нужно знать как "величину" корреляции, так и ее значимость.
Как интерпретировать значения корреляций. Коэффициент корреляции Пирсона (r) представляет собой меру линейной зависимости двух переменных. Если возвести его в квадрат, то полученное значение коэффициента детерминации r2) представляет долю вариации, общую для двух переменных (иными словами, "степень" зависимости или связанности двух переменных). Чтобы оценить зависимость между переменными, нужно знать как "величину" корреляции, так и ее значимость.

Значимость корреляций. Уровень значимости, вычисленный для каждой корреляции, представляет собой главный источник информации о надежности корреляции. Как объяснялось выше (см. Элементарные понятия статистики), значимость определенного коэффициента корреляции зависит от объема выборок. Критерий значимости основывается на предположении, что распределение остатков (т.е. отклонений наблюдений от регрессионной прямой) для зависимой переменной y является нормальным (с постоянной дисперсией для всех значений независимой переменной x). Исследования методом Монте-Карло показали, что нарушение этих условий не является абсолютно критичным, если размеры выборки не слишком малы, а отклонения от нормальности не очень большие.


Тем не менее, имеется несколько серьезных опасностей, о которых следует знать, для этого см. следующие разделы.
Значимость корреляций. Уровень значимости, вычисленный для каждой корреляции, представляет собой главный источник информации о надежности корреляции. Как объяснялось выше (см. Элементарные понятия статистики), значимость определенного коэффициента корреляции зависит от объема выборок. Критерий значимости основывается на предположении, что распределение остатков (т.е. отклонений наблюдений от регрессионной прямой) для зависимой переменной y является нормальным (с постоянной дисперсией для всех значений независимой переменной x). Исследования методом Монте-Карло показали, что нарушение этих условий не является абсолютно критичным, если размеры выборки не слишком малы, а отклонения от нормальности не очень большие. Тем не менее, имеется несколько серьезных опасностей, о которых следует знать, для этого см. следующие разделы.

Выбросы. По определению, выбросы являются нетипичными, резко выделяющимися наблюдениями. Так как при построении прямой регрессии используется сумма квадратов расстояний наблюдаемых точек до прямой, то выбросы могут существенно повлиять на наклон прямой и, следовательно, на значение коэффициента корреляции. Поэтому единичный выброс (значение которого возводится в квадрат) способен существенно изменить наклон прямой и, следовательно, значение корреляции.
Выбросы. По определению, выбросы являются нетипичными, резко выделяющимися наблюдениями. Так как при построении прямой регрессии используется сумма квадратов расстояний наблюдаемых точек до прямой, то выбросы могут существенно повлиять на наклон прямой и, следовательно, на значение коэффициента корреляции. Поэтому единичный выброс (значение которого возводится в квадрат) способен существенно изменить наклон прямой и, следовательно, значение корреляции.

Заметим ,что если размер выборки относительно мал, то добавление или исключение некоторых данных (которые, возможно, не являются "выбросами", как в предыдущем примере) способно оказать существенное влияние на прямую регресии (и коэффициент корреляции).


Это показано в следующем примере, где мы назвали исключенные точки "выбросами"; хотя, возможно, они являются не выбросами, а экстремальными значениями.



Обычно считается, что выбросы представляют собой случайную ошибку, которую следует контролировать. К сожалению, не существует общепринятого метода автоматического удаления выбросов (тем не менее, см. следующий раздел). Чтобы не быть введенными в заблуждение полученными значениями, необходимо проверить на диаграмме рассеяния каждый важный случай значимой корреляции. Очевидно, выбросы могут не только искусственно увеличить значение коэффициента корреляции, но также реально уменьшить существующую корреляцию.

См. также Доверительный эллипс.

Количественный подход к выбросам. Некоторые исследователи применяют численные методы удаления выбросов. Например, исключаются значения, которые выходят за границы ±2 стандартных отклонений (и даже ±1.5 стандартных отклонений) вокруг выборочного среднего. В ряде случаев такая "чистка" данных абсолютно необходима. Например, при изучении реакции в когнитивной психологии, даже если почти все значения экспериментальных данных лежат в диапазоне 300-700 миллисекунд, то несколько "странных времен реакции" 10-15 секунд совершенно меняют общую картину. К сожалению, в общем случае, определение выбросов субъективно, и решение должно приниматься индивидуально в каждом эксперименте (с учетом особенностей эксперимента или "сложившейся практики" в данной области). Следует заметить, что в некоторых случаях относительная частота выбросов к численности групп может быть исследована и разумно проинтерпретирована с точки зрения самой организации эксперимента. См. также Доверительный эллипс.
Количественный подход к выбросам. Некоторые исследователи применяют численные методы удаления выбросов. Например, исключаются значения, которые выходят за границы ±2 стандартных отклонений (и даже ±1.5 стандартных отклонений) вокруг выборочного среднего. В ряде случаев такая "чистка" данных абсолютно необходима.


Например, при изучении реакции в когнитивной психологии, даже если почти все значения экспериментальных данных лежат в диапазоне 300-700 миллисекунд, то несколько "странных времен реакции" 10-15 секунд совершенно меняют общую картину. К сожалению, в общем случае, определение выбросов субъективно, и решение должно приниматься индивидуально в каждом эксперименте (с учетом особенностей эксперимента или "сложившейся практики" в данной области). Следует заметить, что в некоторых случаях относительная частота выбросов к численности групп может быть исследована и разумно проинтерпретирована с точки зрения самой организации эксперимента. См. также Доверительный эллипс.

Корреляции в неоднородных группах. Отсутствие однородности в выборке также является фактором, смещающим (в ту или иную сторону) выборочную корреляцию. Представьте ситуацию, когда коэффициент корреляции вычислен по данным, которые поступили из двух различных экспериментальных групп, что, однако, было проигнорировано при вычислениях. Далее, пусть действия экспериментатора в одной из групп увеличивают значения обеих коррелированных величин, и ,таким образом, данные каждой группы сильно различаются на диаграмме рассеяния (как показано ниже на графике).
Корреляции в неоднородных группах. Отсутствие однородности в выборке также является фактором, смещающим (в ту или иную сторону) выборочную корреляцию. Представьте ситуацию, когда коэффициент корреляции вычислен по данным, которые поступили из двух различных экспериментальных групп, что, однако, было проигнорировано при вычислениях. Далее, пусть действия экспериментатора в одной из групп увеличивают значения обеих коррелированных величин, и ,таким образом, данные каждой группы сильно различаются на диаграмме рассеяния (как показано ниже на графике).

В подобных ситуациях высокая корреляция может быть следствием разбиения данных на две группы, а вовсе не отражать "истинную" зависимость между двумя переменными, которая может практически отсутствовать (это можно заметить, взглянув на каждую группу отдельно, см.


следующий график).



Если вы допускаете такое явление и знаете, как определить "подмножества" данных, попытайтесь вычислить корреляции отдельно для каждого множества. Если вам неясно, как определить подмножества, попытайтесь применить многомерные методы разведочного анализа (например, Кластерный анализ).

Нелинейные зависимости между переменными. Другим возможным источником трудностей, связанным с линейной корреляцией Пирсона r, является форма зависимости. Корреляция Пирсона r хорошо подходит для описания линейной зависимости. Отклонения от линейности увеличивают общую сумму квадратов расстояний от регрессионной прямой, даже если она представляет "истинные" и очень тесные связи между переменными. Итак, еще одной причиной, вызывающей необходимость рассмотрения диаграммы рассеяния для каждого коэффициента корреляции, является нелинейность. Например, следующий график показывает сильную корреляцию между двумя переменными, которую невозможно хорошо описать с помощью линейной функции.
Нелинейные зависимости между переменными. Другим возможным источником трудностей, связанным с линейной корреляцией Пирсона r, является форма зависимости. Корреляция Пирсона r хорошо подходит для описания линейной зависимости. Отклонения от линейности увеличивают общую сумму квадратов расстояний от регрессионной прямой, даже если она представляет "истинные" и очень тесные связи между переменными. Итак, еще одной причиной, вызывающей необходимость рассмотрения диаграммы рассеяния для каждого коэффициента корреляции, является нелинейность. Например, следующий график показывает сильную корреляцию между двумя переменными, которую невозможно хорошо описать с помощью линейной функции.

Измерение нелинейных зависимостей. Что делать, если корреляция сильная, однако зависимость явно нелинейная? К сожалению, не существует простого ответа на данный вопрос, так как не имеется естественного обобщения коэффициента корреляции Пирсона r на случай нелинейных зависимостей.


Однако, если кривая монотонна ( монотонно возрастает или, напротив, монотонно убывает), то можно преобразовать одну или обе переменные, чтобы сделать зависимость линейной, а затем уже вычислить корреляцию между преобразованными величинами. Для этого часто используется логарифмическое преобразование. Другой подход состоит в использовании непараметрической корреляции (например, корреляции Спирмена, см. раздел Непараметрическая статистика и подгонка распределения). Иногда этот метод приводит к успеху, хотя непараметрические корреляции чувствительны только к упорядоченным значениям переменных, например, по определению, они пренебрегают монотонными преобразованиями данных. К сожалению, два самых точных метода исследования нелинейных зависимостей непросты и требуют хорошего навыка "экспериментирования" с данными. Эти методы состоят в следующем: Нужно попытаться найти функцию, которая наилучшим способом описывает данные. После того, как вы определили функцию, можно проверить ее "степень согласия" с данными. Вы можете иметь дело с данными, разбитыми некоторой переменной на группы (например, на 4 или 5 групп). Определите эту переменную как группирующую переменную, а затем примените дисперсионный анализ. Разведочный анализ корреляционных матриц. Во многих исследованиях первый шаг анализа состоит в вычислении корреляционной матрицы всех переменных и проверке значимых (ожидаемых и неожиданных) корреляций. После того как это сделано, следует понять общую природу обнаруженной статистической значимости (см. Элементарные понятия статистики). Иными словами, понять, почему одни коэффициенты корреляции значимы, а другие нет. Однако следует иметь в виду, если используется несколько критериев, значимые результаты могут появляться "удивительно часто", и это будет происходить чисто случайным образом. Например, коэффициент, значимый на уровне .05, будет встречаться чисто случайно один раз в каждом из 20 подвергнутых исследованию коэффициентов. Нет способа автоматически выделить "истинную" корреляцию.


Поэтому следует подходить с осторожностью ко всем не предсказанным или заранее не запланированным результатам и попытаться соотнести их с другими (надежными) результатами. В конечном счете, самый убедительный способ проверки состоит в проведении повторного экспериментального исследования. Такое положение является общим для всех методов анализа, использующих "множественные сравнения и статистическую значимость". Эта проблема также обсуждается в описании процедур Апостериорные сравнения средних и Группировка.
Измерение нелинейных зависимостей. Что делать, если корреляция сильная, однако зависимость явно нелинейная? К сожалению, не существует простого ответа на данный вопрос, так как не имеется естественного обобщения коэффициента корреляции Пирсона r на случай нелинейных зависимостей. Однако, если кривая монотонна (монотонно возрастает или, напротив, монотонно убывает), то можно преобразовать одну или обе переменные, чтобы сделать зависимость линейной, а затем уже вычислить корреляцию между преобразованными величинами. Для этого часто используется логарифмическое преобразование. Другой подход состоит в использовании непараметрической корреляции (например, корреляции Спирмена, см. раздел Непараметрическая статистика и подгонка распределения). Иногда этот метод приводит к успеху, хотя непараметрические корреляции чувствительны только к упорядоченным значениям переменных, например, по определению, они пренебрегают монотонными преобразованиями данных. К сожалению, два самых точных метода исследования нелинейных зависимостей непросты и требуют хорошего навыка "экспериментирования" с данными. Эти методы состоят в следующем: Нужно попытаться найти функцию, которая наилучшим способом описывает данные. После того, как вы определили функцию, можно проверить ее "степень согласия" с данными. Вы можете иметь дело с данными, разбитыми некоторой переменной на группы (например, на 4 или 5 групп). Определите эту переменную как группирующую переменную, а затем примените дисперсионный анализ. Разведочный анализ корреляционных матриц.


Во многих исследованиях первый шаг анализа состоит в вычислении корреляционной матрицы всех переменных и проверке значимых (ожидаемых и неожиданных) корреляций. После того как это сделано, следует понять общую природу обнаруженной статистической значимости (см. Элементарные понятия статистики). Иными словами, понять, почему одни коэффициенты корреляции значимы, а другие нет. Однако следует иметь в виду, если используется несколько критериев, значимые результаты могут появляться "удивительно часто", и это будет происходить чисто случайным образом. Например, коэффициент, значимый на уровне .05, будет встречаться чисто случайно один раз в каждом из 20 подвергнутых исследованию коэффициентов. Нет способа автоматически выделить "истинную" корреляцию. Поэтому следует подходить с осторожностью ко всем не предсказанным или заранее не запланированным результатам и попытаться соотнести их с другими (надежными) результатами. В конечном счете, самый убедительный способ проверки состоит в проведении повторного экспериментального исследования. Такое положение является общим для всех методов анализа, использующих "множественные сравнения и статистическую значимость". Эта проблема также обсуждается в описании процедур Апостериорные сравнения средних и Группировка.

Построчное удаление пропущенных данных в сравнении с попарным удалением. Принятый по умолчанию способ удаления пропущенных данных при вычислении корреляционной матрицы - состоит в построчном удалении наблюдений с пропусками (удаляется вся строка, в которой имеется хотя бы одно пропущенное значение). Этот способ приводит к "правильной" корреляционной матрице в том смысле, что все коэффициенты вычислены по одному и тому же множеству наблюдений. Однако если пропущенные значения распределены случайным образом в переменных, то данный метод может привести к тому, что в рассматриваемом множестве данных не останется ни одного неисключенного наблюдения (в каждой строке наблюдений встретится, по крайней мере, одно пропущенное значение).


Чтобы избежать подобной ситуации, используют другой способ, называемый попарным удалением. В этом способе учитываются только пропуски в каждой выбранной паре переменных и игнорируются пропуски в других переменных. Корреляция между парой переменных вычисляется по наблюдениям, где нет пропусков. Во многих ситуациях, особенно когда число пропусков относительно мало, скажем 10%, и пропуски распределены достаточно хаотично, этот метод не приводит к серьезным ошибкам. Однако, иногда это не так.
Построчное удаление пропущенных данных в сравнении с попарным удалением. Принятый по умолчанию способ удаления пропущенных данных при вычислении корреляционной матрицы - состоит в построчном удалении наблюдений с пропусками (удаляется вся строка, в которой имеется хотя бы одно пропущенное значение). Этот способ приводит к "правильной" корреляционной матрице в том смысле, что все коэффициенты вычислены по одному и тому же множеству наблюдений. Однако если пропущенные значения распределены случайным образом в переменных, то данный метод может привести к тому, что в рассматриваемом множестве данных не останется ни одного неисключенного наблюдения (в каждой строке наблюдений встретится, по крайней мере, одно пропущенное значение). Чтобы избежать подобной ситуации, используют другой способ, называемый попарным удалением. В этом способе учитываются только пропуски в каждой выбранной паре переменных и игнорируются пропуски в других переменных. Корреляция между парой переменных вычисляется по наблюдениям, где нет пропусков. Во многих ситуациях, особенно когда число пропусков относительно мало, скажем 10%, и пропуски распределены достаточно хаотично, этот метод не приводит к серьезным ошибкам. Однако, иногда это не так.

Например, в систематическом смещении (сдвиге) оценки может "скрываться" систематическое расположение пропусков, являющееся причиной различия коэффициентов корреляции, построенных по разным подмножествам. Другая проблема связанная с корреляционной матрицей, вычисленной при попарном удалении пропусков, возникает при использовании этой матрицы в других видах анализа (например, Множественная регрессия, Факторный анализ или Кластерный анализ).


В них предполагается, что используется "правильная" корреляционная матрица с определенным уровнем состоятельности и "соответствия" различных коэффициентов. Использование матрицы с "плохими" (смещенными) оценками приводит к тому, что программа либо не в состоянии анализировать такую матрицу, либо результаты будут ошибочными. Поэтому, если применяется попарный метод исключения пропущенных данных, необходимо проверить, имеются или нет систематические закономерности в распределении пропусков. Как определить смещения, вызванные попарным удалением пропущенных данных. Если попарное исключение пропущенных данных не приводит к какому-либо систематическому сдвигу в оценках, то все эти статистики будут похожи на аналогичные статистики, вычисленные при построчном способе удаления пропусков. Если наблюдается значительное различие, то есть основание предполагать наличие сдвига в оценках. Например, если среднее (или стандартное отклонение) значений переменной A, которое использовалось при вычислении ее корреляции с переменной B, много меньше среднего (или стандартного отклонения) тех же значений переменной A, которые использовались при вычислении ее корреляции с переменной C, то имеются все основания ожидать, что эти две корреляции (A-B и A-C) основаны на разных подмножествах данных, и, таким образом, в оценках корреляций имеется сдвиг, вызванный неслучайным расположением пропусков в значениях переменных.
Как определить смещения, вызванные попарным удалением пропущенных данных. Если попарное исключение пропущенных данных не приводит к какому-либо систематическому сдвигу в оценках, то все эти статистики будут похожи на аналогичные статистики, вычисленные при построчном способе удаления пропусков. Если наблюдается значительное различие, то есть основание предполагать наличие сдвига в оценках. Например, если среднее (или стандартное отклонение) значений переменной A, которое использовалось при вычислении ее корреляции с переменной B, много меньше среднего (или стандартного отклонения) тех же значений переменной A, которые использовались при вычислении ее корреляции с переменной C, то имеются все основания ожидать, что эти две корреляции (A-B и A-C) основаны на разных подмножествах данных, и, таким образом, в оценках корреляций имеется сдвиг, вызванный неслучайным расположением пропусков в значениях переменных.



Попарное удаление пропущенных данных в сравнении с подстановкой среднего значения. Другим общим методом, позволяющим избежать потери наблюдений при построчном способе удаления наблюдений с пропусками, является замена средним (для каждой переменной пропущенные значения заменяются средним значением этой переменной). Подстановка среднего вместо пропусков имеет свои преимущества и недостатки в сравнении с попарным способом удаления пропусков. Основное преимущество в том, что он дает состоятельные оценки, однако имеет следующие недостатки: Подстановка среднего искусственно уменьшает разброс данных, иными словами, чем больше пропусков, тем больше данных, совпадающих со средним значением, искусственно добавленным в данные. Так как пропущенные данные заменяются искусственно созданными "средними", то корреляции могут сильно уменьшиться. Ложные корреляции. Основываясь на коэффициентах корреляции, вы не можете строго доказать причинной зависимости между переменными (см. Элементарные понятия статистики), однако можете определить ложные корреляции, т.е. корреляции, которые обусловлены влияниями "других", остающихся вне вашего поля зрения переменных. Лучше всего понять ложные корреляции на простом примере. Известно, что существует корреляция между ущербом, причиненным пожаром, и числом пожарных, тушивших пожар. Однако эта корреляция ничего не говорит о том, насколько уменьшатся потери, если будет вызвано меньше число пожарных. Причина в том, что имеется третья переменная (начальный размер пожара), которая влияет как на причиненный ущерб, так и на число вызванных пожарных. Если вы будете "контролировать" эту переменную (например, рассматривать только пожары определенной величины), то исходная корреляция (между ущербом и числом пожарных) либо исчезнет, либо, возможно, даже изменит свой знак. Основная проблема ложной корреляции состоит в том, что вы не знаете, кто является ее агентом. Тем не менее, если вы знаете, где искать, то можно воспользоваться частные корреляции, чтобы контролировать (частично исключенное) влияние определенных переменных.


Попарное удаление пропущенных данных в сравнении с подстановкой среднего значения. Другим общим методом, позволяющим избежать потери наблюдений при построчном способе удаления наблюдений с пропусками, является замена средним (для каждой переменной пропущенные значения заменяются средним значением этой переменной). Подстановка среднего вместо пропусков имеет свои преимущества и недостатки в сравнении с попарным способом удаления пропусков. Основное преимущество в том, что он дает состоятельные оценки, однако имеет следующие недостатки: Подстановка среднего искусственно уменьшает разброс данных, иными словами, чем больше пропусков, тем больше данных, совпадающих со средним значением, искусственно добавленным в данные. Так как пропущенные данные заменяются искусственно созданными "средними", то корреляции могут сильно уменьшиться. Ложные корреляции. Основываясь на коэффициентах корреляции, вы не можете строго доказать причинной зависимости между переменными (см. Элементарные понятия статистики), однако можете определить ложные корреляции, т.е. корреляции, которые обусловлены влияниями "других", остающихся вне вашего поля зрения переменных. Лучше всего понять ложные корреляции на простом примере. Известно, что существует корреляция между ущербом, причиненным пожаром, и числом пожарных, тушивших пожар. Однако эта корреляция ничего не говорит о том, насколько уменьшатся потери, если будет вызвано меньше число пожарных. Причина в том, что имеется третья переменная (начальный размер пожара), которая влияет как на причиненный ущерб, так и на число вызванных пожарных. Если вы будете "контролировать" эту переменную (например, рассматривать только пожары определенной величины), то исходная корреляция (между ущербом и числом пожарных) либо исчезнет, либо, возможно, даже изменит свой знак. Основная проблема ложной корреляции состоит в том, что вы не знаете, кто является ее агентом. Тем не менее, если вы знаете, где искать, то можно воспользоваться частные корреляции, чтобы контролировать (частично исключенное) влияние определенных переменных.



Являются ли коэффициенты корреляции "аддитивными"? Нет, не являются. Например, усредненный коэффициент корреляции, вычисленный по нескольким выборкам, не совпадает со "средней корреляцией" во всех этих выборках. Причина в том, что коэффициент корреляции не является линейной функцией величины зависимости между переменными. Коэффициенты корреляции не могут быть просто усреднены. Если вас интересует средний коэффициент корреляции, следует преобразовать коэффициенты корреляции в такую меру зависимости, которая будет аддитивной. Например, до того, как усреднить коэффициенты корреляции, их можно возвести в квадрат, получить коэффициенты детерминации, которые уже будут аддитивными, или преобразовать корреляции в z значения Фишера, которые также аддитивны.
Являются ли коэффициенты корреляции "аддитивными"? Нет, не являются. Например, усредненный коэффициент корреляции, вычисленный по нескольким выборкам, не совпадает со "средней корреляцией" во всех этих выборках. Причина в том, что коэффициент корреляции не является линейной функцией величины зависимости между переменными. Коэффициенты корреляции не могут быть просто усреднены. Если вас интересует средний коэффициент корреляции, следует преобразовать коэффициенты корреляции в такую меру зависимости, которая будет аддитивной. Например, до того, как усреднить коэффициенты корреляции, их можно возвести в квадрат, получить коэффициенты детерминации, которые уже будут аддитивными, или преобразовать корреляции в z значения Фишера, которые также аддитивны.

Как определить, являются ли два коэффициента корреляции значимо различными. Имеется критерий, позволяющий оценить значимость различия двух коэффициентов корреляциями. Результат применения критерия зависит не только от величины разности этих коэффициентов, но и от объема выборок и величины самих этих коэффициентов. В соответствии с ранее обсуждаемыми принципами, чем больше объем выборки, тем меньший эффект мы можем значимо обнаружить. Вообще говоря, в соответствии с общим принципом, надежность коэффициента корреляции увеличивается с увеличением его абсолютного значения, относительно малые различия между большими коэффициентами могут быть значимыми.


Например, разница . 10 между двумя корреляциями может не быть значимой, если коэффициенты равны .15 и .25, хотя для той же выборки разность 0.10 может оказаться значимой для коэффициентов .80 и .90.

Как определить, являются ли два коэффициента корреляции значимо различными. Имеется критерий, позволяющий оценить значимость различия двух коэффициентов корреляциями. Результат применения критерия зависит не только от величины разности этих коэффициентов, но и от объема выборок и величины самих этих коэффициентов. В соответствии с ранее обсуждаемыми принципами, чем больше объем выборки, тем меньший эффект мы можем значимо обнаружить. Вообще говоря, в соответствии с общим принципом, надежность коэффициента корреляции увеличивается с увеличением его абсолютного значения, относительно малые различия между большими коэффициентами могут быть значимыми. Например, разница .10 между двумя корреляциями может не быть значимой, если коэффициенты равны .15 и .25, хотя для той же выборки разность 0.10 может оказаться значимой для коэффициентов .80 и .90.

В начало

t-критерий для независимых выборок

Цель, предположения. t-критерий является наиболее часто используемым методом обнаружения различия между средними двух выборок. Например, t-критерий можно использовать для сравнения средних показателей группы пациентов, принимавших определенное лекарство, с контрольной группой, где принималось безвредное лекарство. Теоретически, t-критерий может применяться, даже если размеры выборок очень небольшие (например, 10; некоторые исследователи утверждают, что можно исследовать выборки меньшего размера), и если переменные нормально распределены (внутри групп), а дисперсии наблюдений в группах не слишком различны (см. также Элементарные понятия статистики). Предположение о нормальности можно проверить, исследуя распределение (например, визуально с помощью гистограммы) или применяя какой-либо критерий нормальности. Равенство дисперсий в двух группах можно проверить с помощью F критерия или использовать более устойчивый критерий Левена.


Если условия применимости t- критерия не выполнены, следует использовать непараметрические альтернативы t-критерия (см. Непараметрическая статистика и подгонка распределения).
Цель, предположения. t-критерий является наиболее часто используемым методом обнаружения различия между средними двух выборок. Например, t-критерий можно использовать для сравнения средних показателей группы пациентов, принимавших определенное лекарство, с контрольной группой, где принималось безвредное лекарство. Теоретически, t-критерий может применяться, даже если размеры выборок очень небольшие (например, 10; некоторые исследователи утверждают, что можно исследовать выборки меньшего размера), и если переменные нормально распределены (внутри групп), а дисперсии наблюдений в группах не слишком различны (см. также Элементарные понятия статистики). Предположение о нормальности можно проверить, исследуя распределение (например, визуально с помощью гистограммы) или применяя какой-либо критерий нормальности. Равенство дисперсий в двух группах можно проверить с помощью F критерия или использовать более устойчивый критерий Левена. Если условия применимости t-критерия не выполнены, следует использовать непараметрические альтернативы t-критерия (см. Непараметрическая статистика и подгонка распределения).

p-уровень значимости t-критерия равен вероятности ошибочно отвергнуть гипотезу о равенстве средних двух выборок, когда в действительности эта гипотеза имеет место. Иными словами, он равен вероятности ошибки принять гипотезу о неравенстве средних, когда в действительности средние равны. Некоторые исследователи предлагают, в случае, когда рассматриваются отличия только в одном направлении (например, рассматривается альтернатива: среднее в первой группе больше (меньше), чем среднее во второй), использовать одностороннее t-распределение и делить р-уровень двустороннего t-критерия пополам. Другие предлагают всегда работать со стандартным двусторонним t-критерием. См. также, t распределение Стьюдента.



Расположение данных. Чтобы применить t- критерий для независимых выборок, требуется, по крайней мере, одна независимая (группирующая) переменная (например, Пол: мужчина/женщина) и одна зависимая переменная (например, тестовое значение некоторого показателя, кровяное давление, число лейкоцитов и т.д.). С помощью специальных значений независимой переменной (эти значения называются кодами, например, мужчина и женщина) данные разбиваются на две группы. Можно произвести анализ следующих данных с помощью t-критерия, сравнивающего среднее WCC для мужчин и женщин.

Расположение данных. Чтобы применить t-критерий для независимых выборок, требуется, по крайней мере, одна независимая (группирующая) переменная (например, Пол: мужчина/женщина) и одна зависимая переменная (например, тестовое значение некоторого показателя, кровяное давление, число лейкоцитов и т.д.). С помощью специальных значений независимой переменной (эти значения называются кодами, например, мужчина и женщина) данные разбиваются на две группы. Можно произвести анализ следующих данных с помощью t-критерия, сравнивающего среднее WCC для мужчин и женщин.

Таблица 1
Таблица 1

ПОЛ WCC наблюдение 1
наблюдение 2
наблюдение 3
наблюдение 4
наблюдение 5   среднее WCC для мужчин = 110
среднее WCC для женщин = 103

мужчина мужчина мужчина женщина женщина	111 110 109 102 104

Графики t-критериев. Анализ данных с помощью t-критерия, сравнения средних и меры отклонения от среднего в группах можно производить с помощью диаграмм размаха (см. график ниже).

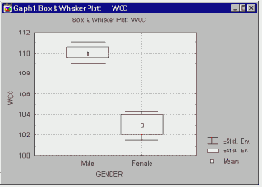
Эти графики позволяют визуально оценить степень зависимости между группирующей и зависимой переменными.

Более сложные групповые сравнения. На практике часто приходится сравнивать более двух групп данных (например, имеется лекарство 1, лекарство 2 и успокоительное лекарство) или сравнивать группы, созданные более чем одной независимой переменной (например, Пол, тип Лекарства и Доза). В таких более сложных исследованиях следует использовать Дисперсионный анализ, который можно рассматривать как обобщение t-критерия.


Фактически в случае однофакторного сравнения двух групп, дисперсионный анализ дает результаты, идентичные t-критерию (t**2 [ст.св.] = F[1,ст.св.]. Однако, если план существенно более сложный, ANOVA предпочтительнее t-критерия (даже если используется последовательность t-критериев).
Более сложные групповые сравнения. На практике часто приходится сравнивать более двух групп данных (например, имеется лекарство 1, лекарство 2 и успокоительное лекарство) или сравнивать группы, созданные более чем одной независимой переменной (например, Пол, тип Лекарства и Доза). В таких более сложных исследованиях следует использовать Дисперсионный анализ, который можно рассматривать как обобщение t-критерия. Фактически в случае однофакторного сравнения двух групп, дисперсионный анализ дает результаты, идентичные t-критерию (t**2 [ст.св.] = F[1,ст.св.]. Однако, если план существенно более сложный, ANOVA предпочтительнее t-критерия (даже если используется последовательность t-критериев).

В начало

t-критерий для зависимых выборок

Внутригрупповая вариация. Как объясняется в разделе Элементарные понятия статистики, степень различия между средними в двух группах зависит от внутригрупповой вариации (дисперсии) переменных. В зависимости от того, насколько различны эти значения для каждой группы, "грубая разность" между групповыми средними показывает более сильную или более слабую степень зависимости между независимой (группирующей) и зависимой переменными. Например, если среднее WCC (число лейкоцитов - White Cell Count) равнялось 102 для мужчин и 104 для женщин, то разность внутригрупповых средних только на величину 2 будет чрезвычайно важной, когда все значения WCC мужчин лежат в интервале от 101 до 103, а все значения WCC женщин - в интервале 103 - 105. В этом случае можно довольно хорошо предсказать WCC (значение зависимой переменной) исходя из пола субъекта (независимой переменной). Однако если та же разность 2 получена из сильно разбросанных данных (например, изменяющихся в пределах от 0 до 200), то этой разностью вполне можно пренебречь.


Таким образом, можно сказать, что уменьшение внутригрупповой вариации увеличивает чувствительность критерия.
Внутригрупповая вариация. Как объясняется в разделе Элементарные понятия статистики, степень различия между средними в двух группах зависит от внутригрупповой вариации (дисперсии) переменных. В зависимости от того, насколько различны эти значения для каждой группы, "грубая разность" между групповыми средними показывает более сильную или более слабую степень зависимости между независимой (группирующей) и зависимой переменными. Например, если среднее WCC (число лейкоцитов - White Cell Count) равнялось 102 для мужчин и 104 для женщин, то разность внутригрупповых средних только на величину 2 будет чрезвычайно важной, когда все значения WCC мужчин лежат в интервале от 101 до 103, а все значения WCC женщин - в интервале 103 - 105. В этом случае можно довольно хорошо предсказать WCC (значение зависимой переменной) исходя из пола субъекта (независимой переменной). Однако если та же разность 2 получена из сильно разбросанных данных (например, изменяющихся в пределах от 0 до 200), то этой разностью вполне можно пренебречь. Таким образом, можно сказать, что уменьшение внутригрупповой вариации увеличивает чувствительность критерия.

Цель. t-критерий для зависимых выборок очень полезен в тех довольно часто возникающих на практике ситуациях, когда важный источник внутригрупповой вариации (или ошибки) может быть легко определен и исключен из анализа. Например, это относится к экспериментам, в которых две сравниваемые группы основываются на одной и той же совокупности наблюдений (субъектов), которые тестировались дважды (например, до и после лечения, до и после приема лекарства). В подобных экспериментах значительная часть внутригрупповой изменчивости (вариации) в обеих группах может быть объяснена индивидуальными различиями субъектов. Заметим, что на самом деле, такая ситуация не слишком отличается от той, когда сравниваемые группы совершенно независимы (см. t-критерий для независимых выборок), где индивидуальные отличия также вносят вклад в дисперсию ошибки.


Однако в случае независимых выборок, вы ничего не сможете поделать с этим, т.к. не сможете определить (или "удалить") часть вариации, связанную с индивидуальными различиями субъектов. Если та же самая выборка тестируется дважды, то можно легко исключить эту часть вариации. Вместо исследования каждой группы отдельно и анализа исходных значений, можно рассматривать просто разности между двумя измерениями (например, "до приема лекарства" и "после приема лекарства") для каждого субъекта. Вычитая первые значения из вторых (для каждого субъекта) и анализируя затем только эти "чистые (парные) разности", вы исключите ту часть вариации, которая является результатом различия в исходных уровнях индивидуумов. Именно так и проводятся вычисления в t-критерии для зависимых выборок. В сравнении с t-критерием для независимых выборок, такой подход дает всегда "лучший" результат (критерий становится более чувствительным).
Цель. t-критерий для зависимых выборок очень полезен в тех довольно часто возникающих на практике ситуациях, когда важный источник внутригрупповой вариации (или ошибки) может быть легко определен и исключен из анализа. Например, это относится к экспериментам, в которых две сравниваемые группы основываются на одной и той же совокупности наблюдений (субъектов), которые тестировались дважды (например, до и после лечения, до и после приема лекарства). В подобных экспериментах значительная часть внутригрупповой изменчивости (вариации) в обеих группах может быть объяснена индивидуальными различиями субъектов. Заметим, что на самом деле, такая ситуация не слишком отличается от той, когда сравниваемые группы совершенно независимы (см. t-критерий для независимых выборок), где индивидуальные отличия также вносят вклад в дисперсию ошибки. Однако в случае независимых выборок, вы ничего не сможете поделать с этим, т.к. не сможете определить (или "удалить") часть вариации, связанную с индивидуальными различиями субъектов.


Если та же самая выборка тестируется дважды, то можно легко исключить эту часть вариации. Вместо исследования каждой группы отдельно и анализа исходных значений, можно рассматривать просто разности между двумя измерениями (например, "до приема лекарства" и "после приема лекарства") для каждого субъекта. Вычитая первые значения из вторых (для каждого субъекта) и анализируя затем только эти "чистые (парные) разности", вы исключите ту часть вариации, которая является результатом различия в исходных уровнях индивидуумов. Именно так и проводятся вычисления в t-критерии для зависимых выборок. В сравнении с t-критерием для независимых выборок, такой подход дает всегда "лучший" результат (критерий становится более чувствительным).

Предположения. Теоретические предположения t-критерия для независимых выборок относятся также к критерию для зависимых выборок. Это означает, что попарные разности должны быть нормально распределены. Если это не выполняется, то можно воспользоваться одним из альтернативных непараметрических критериев.
Предположения. Теоретические предположения t-критерия для независимых выборок относятся также к критерию для зависимых выборок. Это означает, что попарные разности должны быть нормально распределены. Если это не выполняется, то можно воспользоваться одним из альтернативных непараметрических критериев.

См. также, t распределение Стьюдента. Расположение данных. Вы можете применять t-критерий для зависимых выборок к любой паре переменных в наборе данных. Заметим, применение этого критерия мало оправдано, если значения двух переменных несопоставимы. Например, если вы сравниваете среднее WCC в выборке пациентов до и после лечения, но используете различные методы вычисления количественного показателя или другие единицы во втором измерении, то высоко значимые значения t-критерия могут быть получены искусственно, именно за счет изменения единиц измерения. Следующий набор данных может быть проанализирован с помощью t-критерия для зависимых выборок.


Расположение данных. Вы можете применять t-критерий для зависимых выборок к любой паре переменных в наборе данных. Заметим, применение этого критерия мало оправдано, если значения двух переменных несопоставимы. Например, если вы сравниваете среднее WCC в выборке пациентов до и после лечения, но используете различные методы вычисления количественного показателя или другие единицы во втором измерении, то высоко значимые значения t-критерия могут быть получены искусственно, именно за счет изменения единиц измерения. Следующий набор данных может быть проанализирован с помощью t-критерия для зависимых выборок.

Таблица 2
Таблица 2

WCC
до WCC
после наблюдение 1
наблюдение 2
наблюдение 3
наблюдение 4
наблюдение 5
...   средняя разность между WCC
"до" и "после" = 1

111.9 109 143 101 80 ...	113 110 144 102 80.9 ...

Средняя разность между показателями в двух столбцах относительно мала (d=1) по сравнению с разбросом данных (от 80 до 143, в первой выборке). Тем не менее t-критерий для зависимых выборок использует только парные разности, "игнорируя" исходные численные значения и их вариацию. Таким образом, величина этой разности 1 будет сравниваться не с разбросом исходных значений, а с разбросом индивидуальных разностей, который относительно мал: 0.2 (от 0.9 в наблюдении 5 до 1.1 в наблюдении 1). В этой ситуации разность 1 очень большая и может привести к значимому t-значению. Матрицы t-критериев. t-критерий для зависимых выборок может быть вычислен для списков переменных и просмотрен далее как матрица. Пропущенные данные при этом обрабатываются либо построчно, либо попарно, точно так же как при вычислении корреляционных матриц. Все те предостережения, которые относились к использованию этих методов обработки пропусков при вычислении матриц коэффициентов корреляций, остаются в силе при вычислении матриц t-критериев. Именно, возможно: появление артефактов (искусственных результатов) из-за попарного удаления пропусков в t-критерии и возникновение чисто "случайно" значимых результатов. Более сложные групповые сравнения.


Если имеется более двух "зависимых выборок" (например, до лечения, после лечения способом 1 и после лечения способом 2), то можно использовать дисперсионный анализ с повторными измерениями. Повторные измерения в дисперсионном анализе (ANOVA) можно рассматривать как обобщение t-критерия для зависимых выборок, позволяющие увеличить чувствительность анализа. Например, можно одновременно контролировать не только базовый уровень зависимой переменной, но и другие факторы, а также включать в план эксперимента более одной зависимой переменной (многомерный дисперсионный анализ MANOVA; более подробно см. ANOVA/MANOVA).
Матрицы t-критериев. t-критерий для зависимых выборок может быть вычислен для списков переменных и просмотрен далее как матрица. Пропущенные данные при этом обрабатываются либо построчно, либо попарно, точно так же как при вычислении корреляционных матриц. Все те предостережения, которые относились к использованию этих методов обработки пропусков при вычислении матриц коэффициентов корреляций, остаются в силе при вычислении матриц t-критериев. Именно, возможно: появление артефактов (искусственных результатов) из-за попарного удаления пропусков в t-критерии и возникновение чисто "случайно" значимых результатов. Более сложные групповые сравнения. Если имеется более двух "зависимых выборок" (например, до лечения, после лечения способом 1 и после лечения способом 2), то можно использовать дисперсионный анализ с повторными измерениями. Повторные измерения в дисперсионном анализе (ANOVA) можно рассматривать как обобщение t-критерия для зависимых выборок, позволяющие увеличить чувствительность анализа. Например, можно одновременно контролировать не только базовый уровень зависимой переменной, но и другие факторы, а также включать в план эксперимента более одной зависимой переменной (многомерный дисперсионный анализ MANOVA; более подробно см. ANOVA/MANOVA).

В начало

Внутригрупповые описательные статистики и корреляции (группировка)



Цель. Процедура вычисляет описательные статистики и корреляции для зависимых переменных в каждой из нескольких групп, определенных одной или большим числом группирующих (независимых) переменных.
Цель. Процедура вычисляет описательные статистики и корреляции для зависимых переменных в каждой из нескольких групп, определенных одной или большим числом группирующих (независимых) переменных.

Расположение данных. В приводимом ниже примере значения зависимой переменной WCC (число лейкоцитов - White Cell Count) разбиваются на группы кодами двух независимых переменных: Пол (значения: мужчины и женщины) и Рост (значения: высокий и низкий).
Расположение данных. В приводимом ниже примере значения зависимой переменной WCC (число лейкоцитов - White Cell Count) разбиваются на группы кодами двух независимых переменных: Пол (значения: мужчины и женщины) и Рост (значения: высокий и низкий).

Таблица 3
Таблица 3

ПОЛ РОСТ WCC наблюдение 1
наблюдение 2
наблюдение 3
наблюдение 4
наблюдение 5
...

мужчина мужчина мужчина женщина женщина ...	низкий высокий высокий высокий низкий ...	101 110 92 112 95 ...

Результаты группировки представляются следующим образом (предполагается, что Пол - первая независимая переменная, а Рост - вторая). Таблица 4
Таблица 4

Вся выборка Среднее=100 СтдОткл=13 N=120
Мужчины Среднее=99 СтдОткл=13 N=60		Женщины Среднее=101 СтдОткл=13 N=60
Высокие/мужчины Среднее=98 СтдОткл=13 N=30	Низкие/мужчины Среднее=100 СтдОткл=13 N=30	Высокие/женщины Среднее=101 СтдОткл=13 N=30	Низкие/женщины Среднее=101 СтдОткл=13 N=30

Описательные статистики, расположенные в середине таблицы, определяются выбранным порядком независимых переменных. Например, в таблице приведены средние значения для "всех мужчин" и "всех женщин", но не показаны средние для "всех людей высокого роста" или для "всех людей низкого роста", которые можно вычислить, если определить Рост как первую группирующую переменную (а не как вторую).



Статистические тесты для группированных данных. Группировка часто используется как средство разведочного анализа данных. Обычный вопрос, который задает исследователь: являются ли группы, созданные независимыми переменными, действительно различными? Если вы интересуетесь различиями средних, то подходящим тестом является однофакторный дисперсионный анализ (ANOVA) (F критерий). Если интерес представляет различие дисперсий, то можно воспользоваться критерием однородности дисперсий.
Статистические тесты для группированных данных. Группировка часто используется как средство разведочного анализа данных. Обычный вопрос, который задает исследователь: являются ли группы, созданные независимыми переменными, действительно различными? Если вы интересуетесь различиями средних, то подходящим тестом является однофакторный дисперсионный анализ (ANOVA) (F критерий). Если интерес представляет различие дисперсий, то можно воспользоваться критерием однородности дисперсий.

Другие близкие методы анализа данных. Хотя в разведочном анализе данных можно строить классификацию с более чем одной независимой переменной, статистические процедуры, используемые для их анализа, предполагают, что существует только один группирующий фактор (даже если фактически результаты получаются комбинированием определенного числа группирующих переменных). Таким образом, эти статистики не обнаруживают и даже не принимают во внимание наличие возможных взаимодействий между группирующими переменными, когда в действительности такие взаимодействия могут иметь место. Например, вполне естественно допустить, что имеются различия между влиянием одной независимой переменной на зависимую переменную на разных уровнях другой независимой переменной (например, высокие люди могут иметь более низкий показатель WCC, чем низкие, однако, возможно, это относится только к мужчинам; см. "дерево" данных выше). Вы можете объяснить подобные эффекты, проверяя группировку "визуально" (в таблицах и на графиках) и используя различный порядок независимых переменных.


Однако величина или значимость таких эффектов не может быть оценена здесь статистически.
Другие близкие методы анализа данных. Хотя в разведочном анализе данных можно строить классификацию с более чем одной независимой переменной, статистические процедуры, используемые для их анализа, предполагают, что существует только один группирующий фактор (даже если фактически результаты получаются комбинированием определенного числа группирующих переменных). Таким образом, эти статистики не обнаруживают и даже не принимают во внимание наличие возможных взаимодействий между группирующими переменными, когда в действительности такие взаимодействия могут иметь место. Например, вполне естественно допустить, что имеются различия между влиянием одной независимой переменной на зависимую переменную на разных уровнях другой независимой переменной (например, высокие люди могут иметь более низкий показатель WCC, чем низкие, однако, возможно, это относится только к мужчинам; см. "дерево" данных выше). Вы можете объяснить подобные эффекты, проверяя группировку "визуально" (в таблицах и на графиках) и используя различный порядок независимых переменных. Однако величина или значимость таких эффектов не может быть оценена здесь статистически.

Апостериорные сравнения средних. Обычно после получения статистически значимого результата в дисперсионном анализе (ANOVA) желательно знать, какие средние вызвали наблюдаемый эффект (например, какие группы особенно сильно отличаются друг от друга). Конечно, можно выполнить серию простых t-критериев, чтобы сравнить все возможные пары средних. Однако в связи с большим числом парных сравнений, такая процедура чисто случайно увеличивает шансы получения значимого результата. Представьте, вы имеете 20 выборок, по 10 случайных чисел в каждой, и вычислили для них средние. Далее возьмите наибольшее среднее и сравните с наименьшим средним. t-критерий для независимых выборок будет проверять, значимо или нет отличаются эти средние, предполагая, что имеет дело с двумя выборками.


Процедуры апостериорного сравнения специально рассчитаны так, чтобы учитывать более двух выборок.
Апостериорные сравнения средних. Обычно после получения статистически значимого результата в дисперсионном анализе (ANOVA) желательно знать, какие средние вызвали наблюдаемый эффект (например, какие группы особенно сильно отличаются друг от друга). Конечно, можно выполнить серию простых t-критериев, чтобы сравнить все возможные пары средних. Однако в связи с большим числом парных сравнений, такая процедура чисто случайно увеличивает шансы получения значимого результата. Представьте, вы имеете 20 выборок, по 10 случайных чисел в каждой, и вычислили для них средние. Далее возьмите наибольшее среднее и сравните с наименьшим средним. t-критерий для независимых выборок будет проверять, значимо или нет отличаются эти средние, предполагая, что имеет дело с двумя выборками. Процедуры апостериорного сравнения специально рассчитаны так, чтобы учитывать более двух выборок.

Группировка в сравнении с дискриминантным анализом.
Группировка в сравнении с дискриминантным анализом.

Группировку можно рассматривать как первый шаг к другому типу анализа, который исследует различия между группами: Дискриминантный анализ. Аналогично классификации, дискриминантный анализ исследует различия между группами, построенными с помощью значений (кодов) независимой (группирующей) переменной. Однако в дискриминантном анализе, как правило, одновременно рассматривается более одной независимой переменной и определяются "типы" (классы) значений этих переменных. Именно, в дискриминантном анализе находят такие линейные комбинации зависимых переменных, которые наилучшим образом определяют принадлежность наблюдения к определенному классу, причем число классов известно заранее. В частности, с помощью дискриминантного анализа можно проанализировать различия между тремя группами людей, выбравших определенную профессию (например, юрист, физик, инженер), основываясь на их успехах в школе по определенным дисциплинам.


Можно утверждать, что этот анализ "объяснит" выбор профессии успехами по определенным предметам. Таким образом, дискриминантный анализ можно рассматривать как "естественное развитие" простой группировки. Группировка в сравнении c таблицами частот. Другой вид анализа, который не может быть непосредственно проведен с помощью группировки - это сравнения частот (n) в различных группах. Часто значения n в различных ячейках не равны между собой, потому что отнесение субъекта к определенной группе является следствием некоторых субъективных установок экспериментатора, а не результатом случайного выбора. Однако если случайный выбор имеет место, то неравенство частот n в различных группах заставляет предположить, что независимые переменные на самом деле связаны между собой. Например, кросстабуляция уровней независимых переменных Возраст и Образование наиболее вероятно не создаст группы равной величины n, потому что степень образования различна для разных возрастов. Если вы хотите провести такие сравнения, то можете изучить определенные частоты в таблицах сопряженности и испытать различные способы упорядочивания независимых переменных. Однако, для того, чтобы подвергнуть разности частот статистическому исследованию, следует воспользоваться таблицами частот и таблицами сопряженности. Для продвинутого анализа сложных многовходовых таблиц (таблиц со многими входами) используйте Логлинейный анализ или Анализ соответствий.
Группировка в сравнении c таблицами частот. Другой вид анализа, который не может быть непосредственно проведен с помощью группировки - это сравнения частот (n) в различных группах. Часто значения n в различных ячейках не равны между собой, потому что отнесение субъекта к определенной группе является следствием некоторых субъективных установок экспериментатора, а не результатом случайного выбора. Однако если случайный выбор имеет место, то неравенство частот n в различных группах заставляет предположить, что независимые переменные на самом деле связаны между собой.


Например, кросстабуляция уровней независимых переменных Возраст и Образование наиболее вероятно не создаст группы равной величины n, потому что степень образования различна для разных возрастов. Если вы хотите провести такие сравнения, то можете изучить определенные частоты в таблицах сопряженности и испытать различные способы упорядочивания независимых переменных. Однако, для того, чтобы подвергнуть разности частот статистическому исследованию, следует воспользоваться таблицами частот и таблицами сопряженности. Для продвинутого анализа сложных многовходовых таблиц (таблиц со многими входами) используйте Логлинейный анализ или Анализ соответствий.

Графическое представление группировки. Графики часто позволяют обнаружить эффекты (как предполагаемые, так и неожиданные) быстрее, а иногда "лучше", чем численные методы. Категоризованные графики дают возможность строить графики средних, распределений, корреляций и т.д. "на пересечении" групп в соответствующих таблицах (например, категоризованные гистограммы, категоризованные вероятностные графики, категоризованные диаграммы размаха). Следующий график представляет собой категоризованную гистограмму, позволяющую быстро оценить вид данных в каждой группе (группа1-мужчины, группа2-женщины, и т.д.).
Графическое представление группировки. Графики часто позволяют обнаружить эффекты (как предполагаемые, так и неожиданные) быстрее, а иногда "лучше", чем численные методы. Категоризованные графики дают возможность строить графики средних, распределений, корреляций и т.д. "на пересечении" групп в соответствующих таблицах (например, категоризованные гистограммы, категоризованные вероятностные графики, категоризованные диаграммы размаха). Следующий график представляет собой категоризованную гистограмму, позволяющую быстро оценить вид данных в каждой группе (группа1-мужчины, группа2-женщины, и т.д.).

Категоризованная диаграмма размаха (на следующем графике) показывает различия в корреляциях зависимых переменных по группам.





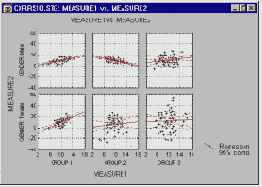
Дополнительно, если программное обеспечение обладает возможностями закрашивания, то вы можете выбрать (т.е. выделить) все точки в матричной диаграмме рассеяния, которые принадлежат к определенной группе, для того чтобы определить, как соответствующие точкам наблюдения влияют на связи между другими переменными в том же наборе данных.

В начало

Таблицы частот

Цель. Таблицы частот или одновходовые таблицы представляют собой простейший метод анализа категориальных (номинальных) переменных (см. Элементарные понятия статистики). Часто их используют как одну из процедур разведочного анализа, чтобы просмотреть, каким образом различные группы данных распределены в выборке. Например, изучая зрительский интерес к разным видам спорта (с целью рекламы какого-либо продукта на ТВ), вы могли бы представить ответы респондентов следующей таблицей:
Цель. Таблицы частот или одновходовые таблицы представляют собой простейший метод анализа категориальных (номинальных) переменных (см. Элементарные понятия статистики). Часто их используют как одну из процедур разведочного анализа, чтобы просмотреть, каким образом различные группы данных распределены в выборке. Например, изучая зрительский интерес к разным видам спорта (с целью рекламы какого-либо продукта на ТВ), вы могли бы представить ответы респондентов следующей таблицей:

Таблица 5
Таблица 5

STATISTICA
ОСНОВНЫЕ
СТАТИСТИКИ ФУТБОЛ: "Просмотр футбола" Категория Частота Кумулят.
частота Процент Кумулят.
процент ВСЕГДА: Всегда интересуюсь
ОБЫЧНО: Обычно интересуюсь
ИНОГДА: Иногда интересуюсь
НИКОГДА: Никогда интересуюсь
Пропущено

39 16 26 19 0	39 55 81 100 100	39.00000 16.00000 26.00000 19.00000 0.00000	39.0000 55.0000 81.0000 100.0000 100.0000

Таблица показывает частоты, кумулятивные (накопленные) частоты, процент, кумулятивный процент респондентов, выразивших свой интерес к просмотру футбольных матчей в следующей шкале: (1) Всегда интересуюсь, (2) Обычно интересуюсь, (3) Иногда интересуюсь или (4) Никогда не интересуюсь. Приложения.


Практически каждый исследовательский проект начинается с построения таблиц частот. Например, в социологических опросах таблицы частот могут отображать число мужчин и женщин, выразивших симпатию тому или иному политическому деятелю, число респондентов из определенной этнических групп, голосовавших за того или иного кандидата и т.д. Ответы, измеренные в определенной шкале (например, в шкале: интерес к футболу) также можно прекрасно свести в таблицу частот. В медицинских исследованиях табулируют пациентов с определенными симптомами. В маркетинговых исследованиях - покупательский спрос на товары разного типа у разных категорий населения. В промышленности - частоту выхода из строя элементов устройства, приведших к авариям или отказам всего устройства при испытаниях на прочность (например, для определения того, какие детали телевизора действительно надежны после эксплуатации в аварийном режиме при большой температуре, а какие нет). Обычно, если в данных имеются группирующие переменные, то для них всегда вычисляются таблицы частот.
Приложения. Практически каждый исследовательский проект начинается с построения таблиц частот. Например, в социологических опросах таблицы частот могут отображать число мужчин и женщин, выразивших симпатию тому или иному политическому деятелю, число респондентов из определенной этнических групп, голосовавших за того или иного кандидата и т.д. Ответы, измеренные в определенной шкале (например, в шкале: интерес к футболу) также можно прекрасно свести в таблицу частот. В медицинских исследованиях табулируют пациентов с определенными симптомами. В маркетинговых исследованиях - покупательский спрос на товары разного типа у разных категорий населения. В промышленности - частоту выхода из строя элементов устройства, приведших к авариям или отказам всего устройства при испытаниях на прочность (например, для определения того, какие детали телевизора действительно надежны после эксплуатации в аварийном режиме при большой температуре, а какие нет). Обычно, если в данных имеются группирующие переменные, то для них всегда вычисляются таблицы частот.

В начало

Таблицы сопряженности и таблицы флагов и заголовков

Цель и расположение данных. Кросстабуляция - это процесс объединения двух ( или нескольких) таблиц частот так, что каждая ячейка (клетка) в построенной таблице представляется единственной комбинацией значений или уровней табулированных переменных. Таким образом, кросстабуляция позволяет совместить частоты появления наблюдений на разных уровнях рассматриваемых факторов. Исследуя эти частоты, можно определить связи между табулированными переменными. Обычно табулируются категориальные (номинальные) переменные или переменные с относительно небольшим числом значений. Если вы хотите табулировать непрерывную переменную (например, доход), то вначале ее следует перекодировать, разбив диапазон изменения на небольшое число интервалов (например, доход: низкий, средний, высокий).
Цель и расположение данных. Кросстабуляция - это процесс объединения двух (или нескольких) таблиц частот так, что каждая ячейка (клетка) в построенной таблице представляется единственной комбинацией значений или уровней табулированных переменных. Таким образом, кросстабуляция позволяет совместить частоты появления наблюдений на разных уровнях рассматриваемых факторов. Исследуя эти частоты, можно определить связи между табулированными переменными. Обычно табулируются категориальные (номинальные) переменные или переменные с относительно небольшим числом значений. Если вы хотите табулировать непрерывную переменную (например, доход), то вначале ее следует перекодировать, разбив диапазон изменения на небольшое число интервалов (например, доход: низкий, средний, высокий).

Таблицы 2x2. Простейшая форма кросстабуляции - это таблица сопряженности 2 x 2, в которой значения двух переменных "пересечены" (сопряжены) на разных уровнях и каждая переменная принимает только два значения, т.е. имеет два уровня (поэтому таблица называется "2 на 2"). К примеру, пусть проводится исследование, в котором мужчины и женщины опрашиваются о том, какой напиток они предпочитают (газированную воду марки A или газированную воду марки B); файл данных может быть таким:


Таблицы 2x2. Простейшая форма кросстабуляции - это таблица сопряженности 2 x 2, в которой значения двух переменных "пересечены" (сопряжены) на разных уровнях и каждая переменная принимает только два значения, т.е. имеет два уровня (поэтому таблица называется "2 на 2"). К примеру, пусть проводится исследование, в котором мужчины и женщины опрашиваются о том, какой напиток они предпочитают (газированную воду марки A или газированную воду марки B); файл данных может быть таким:

Таблица 6
Таблица 6

ПОЛ ГАЗ. ВОДА наблюдение 1
наблюдение 2
наблюдение 3
наблюдение 4
наблюдение 5
...

мужчина женщина женщина женщина мужчина ...	A B B A B ...

Результаты кросстабуляции этих переменных выглядят следующим образом. Таблица 7
Таблица 7

ГАЗ. ВОДА: A ГАЗ. ВОДА: B   ПОЛ: мужчина ПОЛ: женщина

20 (40%)	30 (60%)	50 (50%)
30 (60%)	20 (40%)	50 (50%)
	50 (50%)	50 (50%)	100 (100%)

Каждая ячейка таблицы содержит единственную комбинацию значений двух табулированных переменных (в строке - указана переменная Пол в столбце - переменная марка воды). Числа в каждой ячейке, на пересечении определенной строки и определенного столбца, показывают, сколько наблюдений соответствует данным уровням факторов. В целом таблица показывает, что женщины больше мужчин предпочитают газированную воду марки A, мужчины больше женщин предпочитают марку B. Таким образом, пол и предпочтение могут быть зависимыми (позже будет показано, как эту связь измерить статистически).

Маргинальные частоты. Значения, расположенные по краям таблицы сопряженности - это обычные таблицы частот (с одним входом) для рассматриваемых переменных. Так как эти частоты располагаются на краях таблицы, то они называются маргинальными. Маргинальные значения важны, т.к. позволяют оценить распределение частот в отдельных столбцах и строках таблицы. Например, 40% и 60% мужчин и женщин (соответственно), выбравших марку A (см. первый столбец таблицы), не могли бы показать какой-либо связи между переменными Пол и Газ.вода, если бы маргинальные частоты переменной Пол были также 40% и 60%.


В этом случае они просто отражали бы разную долю мужчин и женщин, участвующих в опросе. Таким образом, различие в распределении частот в строках (или столбцах) отдельных переменных и в соответствующих маргинальных частотах дают информацию о связи переменных.
Маргинальные частоты. Значения, расположенные по краям таблицы сопряженности - это обычные таблицы частот (с одним входом) для рассматриваемых переменных. Так как эти частоты располагаются на краях таблицы, то они называются маргинальными. Маргинальные значения важны, т.к. позволяют оценить распределение частот в отдельных столбцах и строках таблицы. Например, 40% и 60% мужчин и женщин (соответственно), выбравших марку A (см. первый столбец таблицы), не могли бы показать какой-либо связи между переменными Пол и Газ.вода, если бы маргинальные частоты переменной Пол были также 40% и 60%. В этом случае они просто отражали бы разную долю мужчин и женщин, участвующих в опросе. Таким образом, различие в распределении частот в строках (или столбцах) отдельных переменных и в соответствующих маргинальных частотах дают информацию о связи переменных.

Проценты по столбцам, по строкам и проценты от общего числа наблюдений. Пример в предыдущем разделе показывает, что для оценки связи между табулированными переменными, необходимо сравнить маргинальные и индивидуальные частоты в таблице. Такие сравнения легче проводить, имея дело с относительными частотами или процентами.
Проценты по столбцам, по строкам и проценты от общего числа наблюдений. Пример в предыдущем разделе показывает, что для оценки связи между табулированными переменными, необходимо сравнить маргинальные и индивидуальные частоты в таблице. Такие сравнения легче проводить, имея дело с относительными частотами или процентами.

Графическое представление таблиц сопряженности. В целях исследования отдельные строки и столбцы таблицы удобно представлять в виде графиков. Полезно также отобразить целую таблицу на отдельном графике. Таблицы с двумя входами можно изобразить на 3-мерной гистограмме.


Другой способ визуализации таблиц сопряженности - построение категоризованной гистограммы, в которой каждая переменная представлена индивидуальными гистограммами на каждом уровне другой переменной. Преимущество 3М гистограммы в том, что она позволяет представить на одном графике таблицу целиком. Достоинство категоризованного графика в том, что он дает возможность точно оценить отдельные частоты в каждой ячейке.
Графическое представление таблиц сопряженности. В целях исследования отдельные строки и столбцы таблицы удобно представлять в виде графиков. Полезно также отобразить целую таблицу на отдельном графике. Таблицы с двумя входами можно изобразить на 3-мерной гистограмме. Другой способ визуализации таблиц сопряженности - построение категоризованной гистограммы, в которой каждая переменная представлена индивидуальными гистограммами на каждом уровне другой переменной. Преимущество 3М гистограммы в том, что она позволяет представить на одном графике таблицу целиком. Достоинство категоризованного графика в том, что он дает возможность точно оценить отдельные частоты в каждой ячейке.

Таблицы флагов и заголовков. Таблицы флагов и заголовков или, кратко, таблицы заголовков позволяют отобразить несколько двувходовых таблиц в сжатом виде. Этот тип таблиц можно объяснить на примере файла интересов к спорту (см. таблицу ниже). Для краткости, в таблице изображены только строки для категорий Всегда и Обычно.
Таблицы флагов и заголовков. Таблицы флагов и заголовков или, кратко, таблицы заголовков позволяют отобразить несколько двувходовых таблиц в сжатом виде. Этот тип таблиц можно объяснить на примере файла интересов к спорту (см. таблицу ниже). Для краткости, в таблице изображены только строки для категорий Всегда и Обычно.

Таблица 8
Таблица 8

STATISTICA
ОСНОВНЫЕ
СТАТИСТИКИ Таблица флагов и заголовков:
Проценты по строкам Фактор ФУТБОЛ
ВСЕГДА ФУТБОЛ
ОБЫЧНО Всего
по строке БЕЙСБОЛ: ВСЕГДА
БЕЙСБОЛ: ОБЫЧНО БЕЙСБОЛ: Всего ТЕННИС: ВСЕГДА
ТЕННИС: ОБЫЧНО ТЕННИС: Всего БОКС: ВСЕГДА
БОКС: ОБЫЧНО БОКС : Всего

92.31 61.54	7.69 38.46	66.67 33.33
82.05	17.95	100.00
87.50 87.50	12.50 12.50	66.67 33.33
87.50	12.50	100.00
77.78 100.00	22.22 0.00	52.94 47.06
88.24	11.76	100.00

Интерпретация таблиц заголовков. В приведенной выше таблице результатов представлены три двувходовые таблицы, в которых интерес к Футболу сопряжен с интересом к Бейсболу, Теннису и Боксу. Таблица содержит информацию о процентах по столбцам, поэтому суммы по строкам равны 100%. Например, число в левом верхнем углу таблицы результатов (92.31) показывает, что 92.31 процентов всех респондентов ответили, что им всегда интересно смотреть футбол и всегда интересно смотреть баскетбол. Если вы посмотрите следующую часть таблицы, то увидите, что процент тех, кому всегда интересно смотреть футбол и всегда интересно смотреть теннис, равен 87.50; для бокса этот процент составляет 77.78. Проценты в столбце (Всего по строке), показанные после каждого набора переменных, всегда связаны с общим числом наблюдений.
Интерпретация таблиц заголовков. В приведенной выше таблице результатов представлены три двувходовые таблицы, в которых интерес к Футболу сопряжен с интересом к Бейсболу, Теннису и Боксу. Таблица содержит информацию о процентах по столбцам, поэтому суммы по строкам равны 100%. Например, число в левом верхнем углу таблицы результатов (92.31) показывает, что 92.31 процентов всех респондентов ответили, что им всегда интересно смотреть футбол и всегда интересно смотреть баскетбол. Если вы посмотрите следующую часть таблицы, то увидите, что процент тех, кому всегда интересно смотреть футбол и всегда интересно смотреть теннис, равен 87.50; для бокса этот процент составляет 77.78. Проценты в столбце (Всего по строке), показанные после каждого набора переменных, всегда связаны с общим числом наблюдений.

Многовходовые таблицы с категориальными переменными. Когда кросстабулируются только две переменные, результирующая таблица называется двувходовой. Конечно, общую идею кросстабулирования можно обобщить на большее число переменных. В примере с "газированной водой" (см. выше) добавим третью категориальную переменную с информацией о городе, в котором проводилось исследование (Москва или Петербург).


Многовходовые таблицы с категориальными переменными. Когда кросстабулируются только две переменные, результирующая таблица называется двувходовой. Конечно, общую идею кросстабулирования можно обобщить на большее число переменных. В примере с "газированной водой" (см. выше) добавим третью категориальную переменную с информацией о городе, в котором проводилось исследование (Москва или Петербург).

Таблица 9
Таблица 9

ПОЛ ГАЗ. ВОДА ГОРОД наблюдение 1
наблюдение 2
наблюдение 3
наблюдение 4
наблюдение 5
...

мужчина женщина женщина женщина мужчина ...	A B B A B ...	МОСКВА ПЕТЕРБУРГ МОСКВА МОСКВА ПЕТЕРБУРГ ...

Кросстабуляция этих 3-х переменных представлена в следующей таблице: Таблица 10
Таблица 10

ГОРОД: ПЕТЕРБУРГ ГОРОД: МОСКВА   ГАЗ. ВОДА: A ГАЗ. ВОДА: B   ГАЗ. ВОДА: A ГАЗ. ВОДА: B   Пол:мужчина Пол:женщина  

20	30	50	5	45	50
30	20	50	45	5	50
50	50	100	50	50	100

Теоретически любое число переменных может быть кросстабулировано в одной многовходовой таблице. Однако на практике возникают сложности с проверкой и "пониманием" таких таблиц, даже если они содержат более четырех переменных. Рекомендуется анализировать зависимости между факторами в таких таблицах с помощью более продвинутых методов, таких как Логлинейный анализ или Анализ соответствий.

Графическое представление многовходовых таблиц. Вы можете построить "дважды категоризованные" гистограммы, 3М гистограммы
Графическое представление многовходовых таблиц. Вы можете построить "дважды категоризованные" гистограммы, 3М гистограммы

или линейные графики, позволяющие свести частоты для более чем 3-х факторов в один график.



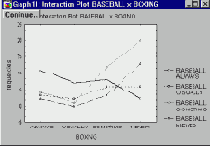
Наборы (каскады) графиков используются для интерпретации сложных многовходовых таблиц (как показано на следующем графике).



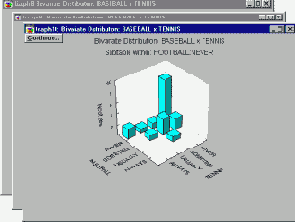
Статистики таблиц сопряженности Обзор Критерий хи-квадрат Пирсона Критерий хи-квадрат (метод максимального правдоподобия) Поправка Йетса Точный критерий Фишера Хи-квадрат Макнемара Коэффициент Фи Тетрахорическая корреляция Коэффициент сопряженности Интерпретация мер связи Статистики, основанные на рангах R Спирмена Тау Кендалла Коэффициент d Соммера: d(X|Y), d(Y|X) Гамма-статистика Коэффициенты неопределенности: S(X,Y), S(X|Y), S(Y|X)


Статистики таблиц сопряженности Обзор Критерий хи-квадрат Пирсона Критерий хи-квадрат (метод максимального правдоподобия) Поправка Йетса Точный критерий Фишера Хи-квадрат Макнемара Коэффициент Фи Тетрахорическая корреляция Коэффициент сопряженности Интерпретация мер связи Статистики, основанные на рангах R Спирмена Тау Кендалла Коэффициент d Соммера: d(X|Y), d(Y|X) Гамма-статистика Коэффициенты неопределенности: S(X,Y), S(X|Y), S(Y|X)

Обзор.
Обзор.

Таблицы сопряженности позволяют измерить связи между кросстабулированными переменными. Следующая таблица отчетливо показывает сильную связь между двумя переменными: переменная Возраст (Взрослый или Ребенок) и переменная - предпочитаемое Печенье (сорт A или сорт B). Таблица 11
Таблица 11

ПЕЧЕНЬЕ: A ПЕЧЕНЬЕ: B   ВОЗРАСТ: ВЗРОСЛЫЙ ВОЗРАСТ: РЕБЕНОК

50	0	50
0	50	50
	50	50	100

Из таблицы видно, что все взрослые выбирают печенье A, а все дети печенье B. В данном случае, нет оснований сомневаться в надежности этого факта. Взглянув на таблицу, мало кто усомнится, что между предпочтениями детей и взрослых имеется отчетливое различие. Однако наблюдаемые на практике связи значительно слабее, и поэтому возникает вопрос: как измерить связи между табулированными переменными и оценить их надежность (статистическую значимость). Далее обсуждаются самые общие меры связи между двумя категоризованными переменными. Методы, используемые для анализа связей между более чем двумя переменными в таблицах высокого порядка, обсуждаются в разделах Логлинейный анализ и Анализ соответствий.

Критерий хи-квадрат Пирсона.
Критерий хи-квадрат Пирсона.

Хи-квадрат Пирсона - это наиболее простой критерий проверки значимости связи между двумя категоризованными переменными. Критерий Пирсона основывается на том, что в двувходовой таблице ожидаемые частоты при гипотезе "между переменными нет зависимости" можно вычислить непосредственно. Представьте, что 20 мужчин и 20 женщин опрошены относительно выбора газированной воды (марка A или марка B).


Если между предпочтением и полом нет связи, то естественно ожидать равного выбора марки A и марки B для каждого пола. Значение статистики хи-квадрат и ее уровень значимости зависит от общего числа наблюдений и количества ячеек в таблице. В соответствии с принципами, обсуждаемыми в разделе Элементарные понятия статистики, относительно малые отклонения наблюдаемых частот от ожидаемых будет доказывать значимость, если число наблюдений велико.

Имеется только одно существенное ограничение использования критерия хи-квадрат (кроме очевидного предположения о случайном выборе наблюдений), которое состоит в том, что ожидаемые частоты не должны быть очень малы. Это связано с тем, что критерий хи-квадрат по своей природе проверяет вероятности в каждой ячейке; и если ожидаемые частоты в ячейках, становятся, маленькими, например, меньше 5, то эти вероятности нельзя оценить с достаточной точностью с помощью имеющихся частот. Дальнейшие обсуждения см. в работах Everitt (1977), Hays (1988) или Kendall and Stuart (1979).

Критерий хи-квадрат (метод максимального правдоподобия). Максимум правдоподобия хи-квадрат предназначен для проверки той же самой гипотезы относительно связей в таблицах сопряженности, что и критерий хи-квадрат Пирсона. Однако его вычисление основано на методе максимального правдоподобия. На практике статистика МП хи-квадрат очень близка по величине к обычной статистике Пирсона хи-квадрат. Подробнее об этой статистике можно прочитать в работах Bishop, Fienberg, and Holland (1975) или Fienberg (1977). В разделе Логлинейный анализ эта статистика обсуждается подробнее.
Критерий хи-квадрат (метод максимального правдоподобия). Максимум правдоподобия хи-квадрат предназначен для проверки той же самой гипотезы относительно связей в таблицах сопряженности, что и критерий хи-квадрат Пирсона. Однако его вычисление основано на методе максимального правдоподобия. На практике статистика МП хи-квадрат очень близка по величине к обычной статистике Пирсона хи-квадрат. Подробнее об этой статистике можно прочитать в работах Bishop, Fienberg, and Holland (1975) или Fienberg (1977).


В разделе Логлинейный анализ эта статистика обсуждается подробнее.

Поправка Йетса. Аппроксимация статистики хи-квадрат для таблиц 2x2 с малыми числом наблюдений в ячейках может быть улучшена уменьшением абсолютного значения разностей между ожидаемыми и наблюдаемыми частотами на величину 0.5 перед возведением в квадрат (так называемая поправка Йетса). Поправка Йетса, делающая оценку более умеренной, обычно применяется в тех случаях, когда таблицы содержат только малые частоты, например, когда некоторые ожидаемые частоты становятся меньше 10 (дальнейшее обсуждение см. в Conover, 1974; Everitt, 1977; Hays, 1988; Kendall and Stuart, 1979 и Mantel, 1974).
Поправка Йетса. Аппроксимация статистики хи-квадрат для таблиц 2x2 с малыми числом наблюдений в ячейках может быть улучшена уменьшением абсолютного значения разностей между ожидаемыми и наблюдаемыми частотами на величину 0.5 перед возведением в квадрат (так называемая поправка Йетса). Поправка Йетса, делающая оценку более умеренной, обычно применяется в тех случаях, когда таблицы содержат только малые частоты, например, когда некоторые ожидаемые частоты становятся меньше 10 (дальнейшее обсуждение см. в Conover, 1974; Everitt, 1977; Hays, 1988; Kendall and Stuart, 1979 и Mantel, 1974).

Точный критерий Фишера. Этот критерий применим только для таблиц 2x2. Критерий основан на следующем рассуждении. Даны маргинальные частоты в таблице, предположим, что обе табулированные переменные независимы. Зададимся вопросом: какова вероятность получения наблюдаемых в таблице частот, исходя из заданных маргинальных? Оказывается, эта вероятность вычисляется точно подсчетом всех таблиц, которые можно построить, исходя из маргинальных. Таким образом, критерий Фишера вычисляет точную вероятность появления наблюдаемых частот при нулевой гипотезе (отсутствие связи между табулированными переменными). В таблице результатов приводятся как односторонние, так и двусторонние уровни.
Точный критерий Фишера. Этот критерий применим только для таблиц 2x2.


Критерий основан на следующем рассуждении. Даны маргинальные частоты в таблице, предположим, что обе табулированные переменные независимы. Зададимся вопросом: какова вероятность получения наблюдаемых в таблице частот, исходя из заданных маргинальных? Оказывается, эта вероятность вычисляется точно подсчетом всех таблиц, которые можно построить, исходя из маргинальных. Таким образом, критерий Фишера вычисляет точную вероятность появления наблюдаемых частот при нулевой гипотезе (отсутствие связи между табулированными переменными). В таблице результатов приводятся как односторонние, так и двусторонние уровни.

Хи-квадрат Макнемара. Этот критерий применяется, когда частоты в таблице 2x2 представляют зависимые выборки. Например, наблюдения одних и тех же индивидуумов до и после эксперимента. В частности, вы можете подсчитывать число студентов, имеющих минимальные успехи по математике в начале и в конце семестра или предпочтение одних и тех же респондентов до и после рекламы. Вычисляются два значения хи-квадрат: A/D и B/C. A/D хи-квадрат проверяет гипотезу о том, что частоты в ячейках A и D (верхняя левая, нижняя правая) одинаковы. B/C хи-квадрат проверяет гипотезу о равенстве частот в ячейках B и C (верхняя правая, нижняя левая).
Хи-квадрат Макнемара. Этот критерий применяется, когда частоты в таблице 2x2 представляют зависимые выборки. Например, наблюдения одних и тех же индивидуумов до и после эксперимента. В частности, вы можете подсчитывать число студентов, имеющих минимальные успехи по математике в начале и в конце семестра или предпочтение одних и тех же респондентов до и после рекламы. Вычисляются два значения хи-квадрат: A/D и B/C. A/D хи-квадрат проверяет гипотезу о том, что частоты в ячейках A и D (верхняя левая, нижняя правая) одинаковы. B/C хи-квадрат проверяет гипотезу о равенстве частот в ячейках B и C (верхняя правая, нижняя левая).

Коэффициент Фи. Фи-квадрат представляет собой меру связи между двумя переменными в таблице 2x2. Его значения изменяются от 0 (нет зависимости между переменными; хи-квадрат = 0.0) до 1 (абсолютная зависимость между двумя факторами в таблице).


Подробности см. в Castellan and Siegel (1988, стр. 232).
Коэффициент Фи. Фи- квадрат представляет собой меру связи между двумя переменными в таблице 2x2. Его значения изменяются от 0 (нет зависимости между переменными; хи-квадрат = 0.0) до 1 (абсолютная зависимость между двумя факторами в таблице). Подробности см. в Castellan and Siegel (1988, стр. 232).

Тетрахорическая корреляция. Эта статистика вычисляется (и применяется) только для таблиц сопряженности 2x2. Если таблица 2x2 может рассматриваться как результат (искусственного) разбиения значений двух непрерывных переменных на два класса, то коэффициент тетрахорической корреляции позволяет оценить зависимость между двумя этими переменными.
Тетрахорическая корреляция. Эта статистика вычисляется (и применяется) только для таблиц сопряженности 2x2. Если таблица 2x2 может рассматриваться как результат (искусственного) разбиения значений двух непрерывных переменных на два класса, то коэффициент тетрахорической корреляции позволяет оценить зависимость между двумя этими переменными.

Коэффициент сопряженности. Коэффициент сопряженности представляет собой основанную на статистике хи-квадрат меру связи признаков в таблице сопряженности (предложенную Пирсоном). Преимущество этого коэффициента перед обычной статистикой хи-квадрат в том, что он легче интерпретируется, т.к. диапазон его изменения находится в интервале от 0 до 1 (где 0 соответствует случаю независимости признаков в таблице, а увеличение коэффициента показывает увеличение степени связи). Недостаток коэффициента сопряженности в том, что его максимальное значение "зависит" от размера таблицы. Этот коэффициент может достигать значения 1 только, если число классов не ограничено (см. Siegel, 1956, стр. 201).
Коэффициент сопряженности. Коэффициент сопряженности представляет собой основанную на статистике хи-квадрат меру связи признаков в таблице сопряженности (предложенную Пирсоном). Преимущество этого коэффициента перед обычной статистикой хи-квадрат в том, что он легче интерпретируется, т.к.


диапазон его изменения находится в интервале от 0 до 1 (где 0 соответствует случаю независимости признаков в таблице, а увеличение коэффициента показывает увеличение степени связи). Недостаток коэффициента сопряженности в том, что его максимальное значение "зависит" от размера таблицы. Этот коэффициент может достигать значения 1 только, если число классов не ограничено (см. Siegel, 1956, стр. 201).

Интерпретация мер связи. Существенный недостаток мер связи (рассмотренных выше) связан с трудностью их интерпретации в обычных терминах вероятности или "доли объясненной вариации", как в случае коэффициента корреляции r Пирсона (см. Корреляции). Поэтому не существует одной общепринятой меры или коэффициента связи.
Интерпретация мер связи. Существенный недостаток мер связи (рассмотренных выше) связан с трудностью их интерпретации в обычных терминах вероятности или "доли объясненной вариации", как в случае коэффициента корреляции r Пирсона (см. Корреляции). Поэтому не существует одной общепринятой меры или коэффициента связи.

Статистики, основанные на рангах. Во многих задачах, возникающих на практике, мы имеем измерения лишь в порядковой шкале (см. Элементарные понятия статистики). Особенно это относится к измерениям в области психологии, социологии и других дисциплинах, связанных с изучением человека. Предположим, вы опросили некоторое множество респондентов с целью выяснения их отношение к некоторым видам спорта. Вы представляете измерения в шкале со следующими позициями: (1) всегда, (2) обычно, (3) иногда и (4) никогда. Очевидно, что ответ иногда интересуюсь показывает меньший интерес респондента, чем ответ обычно интересуюсь и т.д. Таким образом, можно упорядочить (ранжировать) степень интереса респондентов. Это типичный пример порядковой шкалы. Для переменных, измеренных в порядковой шкале, имеются свои типы корреляции, позволяющие оценить зависимости.
Статистики, основанные на рангах. Во многих задачах, возникающих на практике, мы имеем измерения лишь в порядковой шкале (см. Элементарные понятия статистики).


Особенно это относится к измерениям в области психологии, социологии и других дисциплинах, связанных с изучением человека. Предположим, вы опросили некоторое множество респондентов с целью выяснения их отношение к некоторым видам спорта. Вы представляете измерения в шкале со следующими позициями: (1) всегда, (2) обычно, (3) иногда и (4) никогда. Очевидно, что ответ иногда интересуюсь показывает меньший интерес респондента, чем ответ обычно интересуюсь и т.д. Таким образом, можно упорядочить (ранжировать) степень интереса респондентов. Это типичный пример порядковой шкалы. Для переменных, измеренных в порядковой шкале, имеются свои типы корреляции, позволяющие оценить зависимости.

R Спирмена. Статистику R Спирмена можно интерпретировать так же, как и корреляцию Пирсона (r Пирсона) в терминах объясненной доли дисперсии (имея, однако, в виду, что статистика Спирмена вычислена по рангам). Предполагается, что переменные измерены как минимум в порядковой шкале. Всестороннее обсуждение ранговой корреляции Спирмена, ее мощности и эффективности можно найти, например, в книгах Gibbons (1985), Hays (1981), McNemar (1969), Siegel (1956), Siegel and Castellan (1988), Kendall (1948), Olds (1949) и Hotelling and Pabst (1936).
R Спирмена. Статистику R Спирмена можно интерпретировать так же, как и корреляцию Пирсона (r Пирсона) в терминах объясненной доли дисперсии (имея, однако, в виду, что статистика Спирмена вычислена по рангам). Предполагается, что переменные измерены как минимум в порядковой шкале. Всестороннее обсуждение ранговой корреляции Спирмена, ее мощности и эффективности можно найти, например, в книгах Gibbons (1985), Hays (1981), McNemar (1969), Siegel (1956), Siegel and Castellan (1988), Kendall (1948), Olds (1949) и Hotelling and Pabst (1936).

Тау Кендалла. Статистика тау Кендалла эквивалентна R Спирмена при выполнении некоторых основных предположений. Также эквивалентны их мощности. Однако обычно значения R Спирмена и тау Кендалла различны, потому что они отличаются как своей внутренней логикой, так и способом вычисления.


В работе Siegel and Castellan (1988) авторы выразили соотношение между этими двумя статистиками следующим неравенством:
Тау Кендалла. Статистика тау Кендалла эквивалентна R Спирмена при выполнении некоторых основных предположений. Также эквивалентны их мощности. Однако обычно значения R Спирмена и тау Кендалла различны, потому что они отличаются как своей внутренней логикой, так и способом вычисления. В работе Siegel and Castellan (1988) авторы выразили соотношение между этими двумя статистиками следующим неравенством:

-1 < = 3 * Тау Кендалла - 2 * R Спирмена < = 1
-1 < = 3 * Тау Кендалла - 2 * R Спирмена < = 1

Более важно то, что статистики Кендалла тау и Спирмена R имеют различную интерпретацию: в то время как статистика R Спирмена может рассматриваться как прямой аналог статистики r Пирсона, вычисленный по рангам, статистика Кендалла тау скорее основана на вероятности. Более точно, проверяется, что имеется различие между вероятностью того, что наблюдаемые данные расположены в том же самом порядке для двух величин и вероятностью того, что они расположены в другом порядке. Kendall (1948, 1975), Everitt (1977), и Siegel and Castellan (1988) очень подробно обсуждают тау Кендалла. Обычно вычисляется два варианта статистики тау Кендалла: taub и tauc. Эти меры различаются только способом обработки совпадающих рангов. В большинстве случаев их значения довольно похожи. Если возникают различия, то, по-видимому, самый безопасный способ - рассматривать наименьшее из двух значений.

Коэффициент d Соммера: d(X|Y), d(Y|X). Статистика d Соммера представляет собой несимметричную меру связи между двумя переменными. Эта статистика близка к taub (см. Siegel and Castellan, 1988, стр. 303-310).
Коэффициент d Соммера: d(X|Y), d(Y|X). Статистика d Соммера представляет собой несимметричную меру связи между двумя переменными. Эта статистика близка к taub (см. Siegel and Castellan, 1988, стр. 303-310).

Гамма-статистика. Если в данных имеется много совпадающих значений, статистика гамма предпочтительнее R Спирмена или тау Кендалла.


С точки зрения основных предположений, статистика гамма эквивалентна статистике R Спирмена или тау Кендалла. Ее интерпретация и вычисления более похожи на статистику тау Кендалла, чем на статистику R Спирмена. Говоря кратко, гамма представляет собой также вероятность; точнее, разность между вероятностью того, что ранговый порядок двух переменных совпадает, минус вероятность того, что он не совпадает, деленную на единицу минус вероятность совпадений. Таким образом, статистика гамма в основном эквивалентна тау Кендалла, за исключением того, что совпадения явно учитываются в нормировке. Подробное обсуждение статистики гамма можно найти у Goodman and Kruskal (1954, 1959, 1963, 1972), Siegel (1956) и Siegel and Castellan (1988).
Гамма-статистика. Если в данных имеется много совпадающих значений, статистика гамма предпочтительнее R Спирмена или тау Кендалла. С точки зрения основных предположений, статистика гамма эквивалентна статистике R Спирмена или тау Кендалла. Ее интерпретация и вычисления более похожи на статистику тау Кендалла, чем на статистику R Спирмена. Говоря кратко, гамма представляет собой также вероятность; точнее, разность между вероятностью того, что ранговый порядок двух переменных совпадает, минус вероятность того, что он не совпадает, деленную на единицу минус вероятность совпадений. Таким образом, статистика гамма в основном эквивалентна тау Кендалла, за исключением того, что совпадения явно учитываются в нормировке. Подробное обсуждение статистики гамма можно найти у Goodman and Kruskal (1954, 1959, 1963, 1972), Siegel (1956) и Siegel and Castellan (1988).

Коэффициенты неопределенности. Эти коэффициенты измеряют информационную связь между факторами (строками и столбцами таблицы). Понятие информационной зависимости берет начало в теоретико-информационном подходе к анализу таблиц частот, можно обратиться к соответствующим руководствам для разъяснения этого вопроса (см. Kullback, 1959; Ku and Kullback, 1968; Ku, Varner, and Kullback, 1971; см. также Bishop, Fienberg, and Holland, 1975, стр. 344-348).


Статистика S(Y,X) является симметричной и измеряет количество информации в переменной Y относительно переменной X или в переменной X относительно переменной Y. Статистики S(X|Y) и S(Y|X) выражают направленную зависимость.
Коэффициенты неопределенности. Эти коэффициенты измеряют информационную связь между факторами (строками и столбцами таблицы). Понятие информационной зависимости берет начало в теоретико-информационном подходе к анализу таблиц частот, можно обратиться к соответствующим руководствам для разъяснения этого вопроса (см. Kullback, 1959; Ku and Kullback, 1968; Ku, Varner, and Kullback, 1971; см. также Bishop, Fienberg, and Holland, 1975, стр. 344-348). Статистика  S(Y,X) является симметричной и измеряет количество информации в переменной Y относительно переменной X или в переменной X относительно переменной Y. Статистики S(X|Y) и S(Y|X) выражают направленную зависимость.

Многомерные отклики и дихотомии. Переменные типа многомерных откликов и многомерных дихотомий возникают в ситуациях, когда исследователя интересуют не только "простые" частоты событий, но также некоторые (часто неструктурированные) качественные свойства этих событий. Природу многомерных переменных (факторов) лучше всего понять на примерах. Многомерные отклики Многомерные дихотомии Кросстабуляция многомерных откликов и дихотомий Парная кросстабуляция переменных с многомерными откликами Заключительный комментарий
Многомерные отклики и дихотомии. Переменные типа многомерных откликов и многомерных дихотомий возникают в ситуациях, когда исследователя интересуют не только "простые" частоты событий, но также некоторые (часто неструктурированные) качественные свойства этих событий. Природу многомерных переменных (факторов) лучше всего понять на примерах. Многомерные отклики Многомерные дихотомии Кросстабуляция многомерных откликов и дихотомий Парная кросстабуляция переменных с многомерными откликами Заключительный комментарий

Многомерные отклики.


Многомерные отклики.

Представьте, что в процессе большого маркетингового исследования, вы попросили покупателей назвать 3 лучших, с их точки зрения, безалкогольных напитка. Обычный вопрос может выглядеть следующим образом: Напишите ниже три ваших любимых безалкогольных напитка:
Напишите ниже три ваших любимых безалкогольных напитка:

1:__________    2:__________    3:__________

            1:__________    2:__________    3:__________

Анкета содержит от 0 до 3 ответов. Очевидно, список напитков может быть очень большим. Ваша цель - свести результаты в таблицу, в которой, например, будет подсчитан процент респондентов, предпочитающих определенный напиток.

Следующий шаг после получения анкет - занесение ответов в файл данных. Предположим, в ответах упоминалось 50 различных напитков. Вы могли бы, конечно, создать 50 переменных - одну для каждого напитка, рассмотреть респондентов как наблюдения (строки таблицы), ввести код 1 для респондента и переменной, если он предпочитают данный напиток (0, если нет); например:

Таблица 12
Таблица 12

КОКА-КОЛА ПЕПСИ СПРАЙТ . . . . наблюдение 1
наблюдение 2
наблюдение 3
...

0 1 0 ...	1 1 0 ...	0 0 1 ...

Такой метод кодирования откликов, т.е. приписывания им конкретных значений, очевидно, "расточителен". Заметим, что каждый респондент дает максимум 3 ответа; однако для кодирования используется 50 переменных. (Если вы интересуетесь только тремя напитками, то такой метод кодирования будет успешным. Чтобы табулировать предпочтения в выборе напитка, следует рассмотреть 3 переменные, как одну многомерную дихотомию; см. ниже.)

Кодирование многомерных откликов.
Кодирование многомерных откликов.

Более разумным является следующий подход. Введите 3 переменные и определите схему кодирования для 50 напитков. Затем введите соответствующие коды (альфа метки) для значений переменных и получите таблицу следующего вида.



Таблица 13
Таблица 13

Ответ 1 Ответ 2 Ответ 3 наблюдение 1
наблюдение 2
наблюдение 3
 . . .

КОКА-КОЛА СПРАЙТ ПЕРЬЕ  . . .	ПЕПСИ ФАНТА 7 АП  . . .	ДЖОЛТ ДОКТОР ПЕППЕР ОРАНЖ  . . .

Теперь, чтобы получить число респондентов, предпочитающих определенный напиток, рассмотрите переменные Ответ 1 - Ответ 3 как переменную с многомерным откликом. Таблица значений такой переменной имеет вид:

Таблица 14
Таблица 14

N=500
Категория Частота Процент
ответов Процент
наблюдений КОЛА: Кока Кола
ПЕПСИ: Пепси Кола
СПРАЙТ: Спрайт
ПЕППЕР: Доктор Пеппер
 . . .  : . . . .  

44 43 81 74 ..	5.23 5.11 9.62 8.79 ...	8.80 8.60 16.20 14.80 ...
842	100.00	168.40

Интерпретация таблиц частот с многомерными откликами.
Интерпретация таблиц частот с многомерными откликами.

Итак, общее число респондентов в опросе n=500. Заметьте, что числа в первой колонке таблицы не составляют в сумме 500, как можно было бы ожидать, а равны 842. Вы поймете, почему это так, если вспомните, что каждый респондент может дать несколько ответов. Возвращаясь к примеру, видим, что первое наблюдение (Кола, Пепси, Джолт) "дает" три вклада в таблицу частот: в категорию Кола, в категорию Пепси и в категорию Джолт. Второй и третий столбцы таблицы содержат проценты относительного числа ответов (второй столбец) и наблюдений (третий столбец). Таким образом, число 8.80 в первой строке и в последнем столбце таблицы означает, что 8.8% всех респондентов выбрали Кола первым, вторым или третьим пунктом ответа.

Многомерные дихотомии. Предположим, вас интересуют только Кола, Пепси и Спрайт. Как отмечалось, одним из способов кодирования является следующий:
Многомерные дихотомии. Предположим, вас интересуют только Кола, Пепси и Спрайт. Как отмечалось, одним из способов кодирования является следующий:

Таблица 15
Таблица 15

КОЛА ПЕПСИ СПРАЙТ . . . . наблюдение 1
наблюдение 2
наблюдение 3
. . .

1   . . .	1 1   . . .	1 . . .

Здесь каждая переменная используется для одного напитка. Код 1 будет введен в таблицу для переменной каждый раз, когда соответствующий респондент указал ее в своем ответе. Заметим, что каждая переменная является дихотомией, т.к. принимает только два значения: "1" и "не 1" (можно ввести 1 и 0, но так обычно не делается, можно просто рассматривать 0 как пустую ячейку или пропуск). Когда табулируются такие значения, вы получите итоговую таблицу, очень похожую на ту, что была показана раньше для переменных с многомерными откликами; из нее вы можете вычислить число и процент респондентов (и ответов) для каждого напитка. Таким образом, вы компактно представили три переменные - Кола, Пепси, Спрайт одной переменной (Безалкогольные напитки) - многомерной дихотомией.

Кросстабуляция многомерных откликов и дихотомий. Все эти типы переменных можно использовать в таблицах сопряженности. Например, вы можете объединить многомерную дихотомию Безалкогольные напитки (закодированную, как описано выше) с многомерным откликом Любимая еда (со многими категориями, например, Гамбургеры, Пицца и т.д.), а также с простой группирующей переменной Пол. Как и в таблице частот для обычных переменных, в таблице частот для многомерных переменных, можно вычислить проценты и маргинальные суммы или по общему числу респондентов или по общему числу ответов (откликов). Например, рассмотрим следующего гипотетического респондента:
Кросстабуляция многомерных откликов и дихотомий. Все эти типы переменных можно использовать в таблицах сопряженности. Например, вы можете объединить многомерную дихотомию Безалкогольные напитки (закодированную, как описано выше) с многомерным откликом Любимая еда (со многими категориями, например, Гамбургеры, Пицца и т.д.), а также с простой группирующей переменной Пол. Как и в таблице частот для обычных переменных, в таблице частот для многомерных переменных, можно вычислить проценты и маргинальные суммы или по общему числу респондентов или по общему числу ответов (откликов).


Например, рассмотрим следующего гипотетического респондента:

Таблица 16
Таблица 16

Пол Кола Пепси Спрайт Еда1 Еда2 женщина

1	1		РЫБА	ПИЦЦА

Эта женщина назвала Кола и Пепси своими любимыми напитками, а Рыбу и Пиццу - любимыми блюдами. В полной таблице сопряженности этот респондент будет представлен следующими наборами:

Таблица 17
Таблица 17

  Еда . . .  
Всего
ответов Пол Напиток ГАМБУРГЕР РЫБА ПИЦЦА . . .

женщина     мужчина	КОЛА ПЕПСИ СПРАЙТ КОЛА ПЕПСИ СПРАЙТ		X X	X X		2 2

Данный респондент учитывается в таблице 4 раза. Дополнительно, он будет считаться дважды в столбце Женщина - КОЛА маргинальных частот, если этот столбец выводится для представления общего числа откликов. Если пользователь запрашивает маргинальные суммы, вычисленные как общее число респондентов, тогда этот респондент будет учитываться только один раз.

Парная кросстабуляция переменных с многомерными откликами. Особенность процедуры табулирования многомерных переменных состоит в их попарном рассмотрении. Лучше всего показать это на простом примере. Предположим, проводится обследование нынешних и бывших домовладений респондента. Вы попросили респондента описать три последних дома, которыми он владел (включая тот, которым он владеет в данный момент). Естественно, для некоторых из респондентов нынешний дом является самым первым (до этого они не приобретали дома в частную собственность). Другие владели домами раньше. Для каждого дома респондента просят написать количество квартир и число жильцов - членов семьи. Ниже показано, как ответ одного респондента (скажем, наблюдение 112) может быть введен в файл данных:
Парная кросстабуляция переменных с многомерными откликами. Особенность процедуры табулирования многомерных переменных состоит в их попарном рассмотрении.


Лучше всего показать это на простом примере. Предположим, проводится обследование нынешних и бывших домовладений респондента. Вы попросили респондента описать три последних дома, которыми он владел (включая тот, которым он владеет в данный момент). Естественно, для некоторых из респондентов нынешний дом является самым первым (до этого они не приобретали дома в частную собственность). Другие владели домами раньше. Для каждого дома респондента просят написать количество квартир и число жильцов - членов семьи. Ниже показано, как ответ одного респондента (скажем, наблюдение 112) может быть введен в файл данных:

Таблица 18
Таблица 18

Наблюдение Число комнат 1   2   3  Число жильцов  1   2   3 

112		3	3	4		2	3	5

Респондент имел три дома: первый из 3-х комнат, второй также из 3-х комнат, третий из 4-х комнат. Количество членов семьи также росло: в первом доме жило 2 человека, во втором - 3, в третьем - 5.

Пусть вы хотите кросстабулировать число комнат с числом жильцов для всех респондентов (например, чтобы понять, как количество комнат связано с числом жильцов). Один из способов - создать 3 различные таблицы с двумя входами; одну таблицу для одного дома. Вы можете также рассмотреть два фактора в этом исследовании (Число комнат, Число жильцов) как переменные со многими откликами. Однако, очевидно, нет никакого смысла в приведенном примере с респондентом 112 учитывать значения 3 и 5 в ячейке Комнаты - Жильцы в таблице сопряженности (которые вы могли бы учитывать, если бы рассматривали два эти фактора как одинарные переменные с многомерными откликами). Другими словами, вы хотите игнорировать комбинацию жильцов в третьем доме с числом комнат в первом. Скорее всего, вам нужно рассматривать переменные попарно; вы хотели бы рассмотреть число комнат в первом доме вместе с числом жильцов в первом доме, число комнат во втором доме вместе с числом жильцов в нем и т.д.


Так именно и происходит, когда программа выполняет парную кросстабуляцию многомерных переменных.

Заключительный комментарий. Иногда при создании сложных таблиц сопряженности с переменными - многомерными откликами и дихотомиями, возникает следующий вопрос (в ваших исследованиях): "какую дорогу выбрать" или как точно будут учитываться наблюдения в файле данных. Лучший способ проверить, как строится соответствующая таблица - рассмотреть простой пример, и по нему ясно увидеть, каким образом учитывается каждое наблюдение (какой оно вносит вклад). В примерах к разделу Кросстабуляции используется именно такой метод, для того чтобы показать, как вычисляются данные для таблиц с переменными - многомерными откликами и многомерными дихотомиями.
Заключительный комментарий. Иногда при создании сложных таблиц сопряженности с переменными - многомерными откликами и дихотомиями, возникает следующий вопрос (в ваших исследованиях): "какую дорогу выбрать" или как точно будут учитываться наблюдения в файле данных. Лучший способ проверить, как строится соответствующая таблица - рассмотреть простой пример, и по нему ясно увидеть, каким образом учитывается каждое наблюдение (какой оно вносит вклад). В примерах к разделу Кросстабуляции используется именно такой метод, для того чтобы показать, как вычисляются данные для таблиц с переменными - многомерными откликами и многомерными дихотомиями.

Дополнительная информация по методам анализа данных, добычи данных, визуализации и прогнозированию содержится на Портале StatSoft (http://www.statsoft.ru/home/portal/default.asp) и в Углубленном Учебнике StatSoft (Учебник с формулами).

В начало

(c) Copyright StatSoft, Inc., 1984-2001
STATISTICA является торговой маркой StatSoft, Inc.

Планирование эксперимента

Планирование эксперимента

Обзор Эксперименты в науке и промышленности Различия в методике Обзор Общие идеи Вычислительные проблемы Компоненты дисперсии, синтез деноминатора Выводы Дробные 2**(k-p) факторные планы Основная идея Построение плана Разрешение плана Планы Плакетта - Бермана (матрица Адамара) для отсеивания Усиление разрешения плана методом инверсии Псевдонимы для взаимодействий: генераторы плана Разбиение на блоки Повторение плана Добавление центральных точек (центроидов) Анализ результатов эксперимента 2**(k-p) Графические опции Выводы Максимально несмешанные 2**(k-p) планы Основная идея Критерий плана Выводы Планы 3**(k-p), планы Бокса-Бенкена и смешанные 2-х и 3-х уровневые планы Обзор Планирование экспериментов 3**(k-p) Пример плана 3**(4-1) в 9 блоках Планы Бокса-Бенкена Анализ плана 3**(k-p) Дисперсионный анализ Графическое представление результатов Планы для факторов на 2-х и 3-х уровнях Центральные композиционные планы и нефакторные планы для поверхности отклика Обзор Соображения относительно плана Альфа для ротатабельности и ортогональности Доступные стандартные планы Анализ центральных композиционных планов Подогнанная поверхность отклика Категоризованные поверхности отклика Планы на латинских квадратах Обзор Планы на латинских квадратах Анализ плана Очень большие планы, случайные эффекты, несбалансированные вложения Методы Тагучи: робастное планирование эксперимента Обзор Функции качества и потерь качества Отношения (С/Ш) сигнал/шум Ортогональные массивы Анализ планов Аккумуляционный анализ Выводы Планы для смесей и тернарные поверхности Обзор Треугольные координаты Тернарные поверхности и контуры Канонический вид полиномов для смесей Общие модели для смесей Стандартные планы экспериментов для смесей Ограничения снизу Ограничения сверху и снизу Анализ экспериментов для смесей Дисперсионный анализ Оценки параметров Псевдокомпоненты Графические опции Планы для поверхностей и смесей с ограничениями Обзор Планы для экспериментальных областей с ограничениями Линейные ограничения Алгоритм Пипеля и Сни Выбор точек эксперимента Анализ планов для поверхностей и смесей с ограничениями Построение D- и A-оптимальных планов Обзор Основные идеи Измерение эффективности плана Построение оптимальных планов Общие рекомендации Устранение вырожденности матрицы “Подправление” планов Ограниченные экспериментальные области и оптимальный план Специальные разделы Создание профиля предсказанного и желательного отклика Анализ остатков Преобразование Бокса-Кокса зависимых переменных

Обзор Эксперименты в науке и промышленности Различия в методике Обзор Общие идеи Вычислительные проблемы Компоненты дисперсии, синтез деноминатора Выводы Дробные 2**(k-p) факторные планы Основная идея Построение плана Разрешение плана Планы Плакетта - Бермана (матрица Адамара) для отсеивания Усиление разрешения плана методом инверсии Псевдонимы для взаимодействий: генераторы плана Разбиение на блоки Повторение плана Добавление центральных точек (центроидов) Анализ результатов эксперимента 2**(k-p) Графические опции Выводы Максимально несмешанные 2**(k-p) планы Основная идея Критерий плана Выводы Планы 3**(k-p), планы Бокса-Бенкена и смешанные 2-х и 3-х уровневые планы Обзор Планирование экспериментов 3**(k-p) Пример плана 3**(4-1) в 9 блоках Планы Бокса-Бенкена Анализ плана 3**(k-p) Дисперсионный анализ Графическое представление результатов Планы для факторов на 2-х и 3-х уровнях Центральные композиционные планы и нефакторные планы для поверхности отклика Обзор Соображения относительно плана Альфа для ротатабельности и ортогональности Доступные стандартные планы Анализ центральных композиционных планов Подогнанная поверхность отклика Категоризованные поверхности отклика Планы на латинских квадратах Обзор Планы на латинских квадратах Анализ плана Очень большие планы, случайные эффекты, несбалансированные вложения Методы Тагучи: робастное планирование эксперимента Обзор Функции качества и потерь качества Отношения (С/Ш) сигнал/шум Ортогональные массивы Анализ планов Аккумуляционный анализ Выводы Планы для смесей и тернарные поверхности Обзор Треугольные координаты Тернарные поверхности и контуры Канонический вид полиномов для смесей Общие модели для смесей Стандартные планы экспериментов для смесей Ограничения снизу Ограничения сверху и снизу Анализ экспериментов для смесей Дисперсионный анализ Оценки параметров Псевдокомпоненты Графические опции Планы для поверхностей и смесей с ограничениями Обзор Планы для экспериментальных областей с ограничениями Линейные ограничения Алгоритм Пипеля и Сни Выбор точек эксперимента Анализ планов для поверхностей и смесей с ограничениями Построение D- и A-оптимальных планов Обзор Основные идеи Измерение эффективности плана Построение оптимальных планов Общие рекомендации Устранение вырожденности матрицы “Подправление” планов Ограниченные экспериментальные области и оптимальный план Специальные разделы Создание профиля предсказанного и желательного отклика Анализ остатков Преобразование Бокса-Кокса зависимых переменных



Обзор

Эксперименты в науке и промышленности Экспериментальные методы широко используются как в науке, так и в промышленности, однако нередко с весьма различными целями. Обычно основная цель научного исследования состоит в том, чтобы показать статистическую значимость эффекта воздействия определенного фактора на изучаемую зависимую переменную (подробнее о понятии статистической значимости см. в главе Элементарные понятия статистики, т. I).
Эксперименты в науке и промышленности Экспериментальные методы широко используются как в науке, так и в промышленности, однако нередко с весьма различными целями. Обычно основная цель научного исследования состоит в том, чтобы показать статистическую значимость эффекта воздействия определенного фактора на изучаемую зависимую переменную (подробнее о понятии статистической значимости см. в главе Элементарные понятия статистики, т. I).

В условиях промышленного эксперимента основная цель обычно заключается в извлечении максимального количества объективной информации о влиянии изучаемых факторов на производственный процесс с помощью наименьшего числа дорогостоящих наблюдений. Если в научных приложениях методы дисперсионного анализа используются для выяснения реальной природы взаимодействий, проявляющейся во взаимодействии факторов высших порядков, то в промышленности учет эффектов взаимодействия факторов часто считается излишним в ходе выявления существенно влияющих факторов. Различия в методике
Различия в методике

Указанное отличие приводит к существенному различию методов, применяемых в науке и промышленности. Если просмотреть классические учебники по дисперсионному анализу, например, монографии Винера (1962) или Кеппеля (1982), то обнаружится, что в них, в основном, обсуждаются планы с количеством факторов не более пяти (планы же с более чем шестью факторами обычно оказываются бесполезными: подробнее см. в разделе Вводный обзор главы Дисперсионный анализ). Основное внимание в данных рассуждениях сосредоточено на выборе общезначимых и устойчивых критериев значимости.


Однако если обратиться к стандартным учебникам по экспериментам в промышленности (например, Бокс, Хантер и Хантер (1978); Бокс и Дрейпер (1987); Мейсон, Ганс и Гесс (1989); Тагучи (1987)), то окажется, что в них обсуждаются, в основном, многофакторные планы (например, с 16-ю или 32-мя факторами), в которых нельзя оценить эффекты взаимодействия, и основное внимание сосредоточивается на том получении несмещенных оценок главных эффектов (или, реже, взаимодействий второго порядка) с использованием наименьшего числа наблюдений. Это сравнение можно продолжить, но после того как вы получите более подробную информацию о планировании промышленных экспериментов, различия станут еще более очевидны. Отметим, что глава Дисперсионный анализ содержит подробное обсуждение типичных вопросов, касающихся планирования эксперимента в научных исследованиях, а модуль Дисперсионный анализ системы STATISTICA представляет исчерпывающую реализацию общей линейной модели в дисперсионном и ковариационном анализе (как одномерном, так и многомерном). Разумеется, существует немало промышленных приложений, в которых с успехом используются обычные планы дисперсионного анализа, зарекомендовавшие себя в научных исследованиях. Для того, чтобы составить более общее впечатление о совокупности методов, объединенных понятием Планирование эксперимента, будет полезно обратиться к разделу Вводный обзор главы Дисперсионный анализ. Обзор
Обзор

В следующих параграфах обсуждаются общие идеи и принципы, на которых основано планирование промышленных экспериментов, а также описываются используемые типы планов. Эти параграфы близки по своему характеру к вводным. Предполагается, что вы уже знакомы с основными идеями дисперсионного анализа и способами интерпретации главных эффектов и взаимодействий. Мы рекомендуем перечитать раздел Вводный обзор главы Дисперсионный анализ перед тем, как продолжить чтение. Общие идеи
Общие идеи

Обычно любая машина или станок, используемый на производстве, позволяет операторам изменять различные настройки, влияя на качество производимого продукта.


Эксперименты позволяют инженеру, ответственному за производство, улучшать настройки машины, а также выяснить какие факторы вносят наиболее важный вклад в качество продукции. Использование этой информации позволяет улучшить настройки системы, достигнув оптимального качества. Чтобы проиллюстрировать эти рассуждения ниже приводится несколько примеров.

Пример 1: Производство красителей для ткани. В книге Бокса и Дрейпера (Бокс и Дрейпер (1987), стр. 115) рассказывается об эксперименте по производству некоторого красителя для ткани. В этом случае качество производимой продукции описывается насыщенностью, яркостью и стойкостью окрашеной ткани. Кроме того, необходимо уточнить, что надо изменять для получения красок различной насыщенности, яркости для удовлетворения потребительского спроса. Другими словами, в этом эксперименте нужно выявить факторы, наиболее заметно влияющие на яркость, насыщенность и стойкость производимой краски. В примере Бокса и Дрейпера рассматривается 6 различных факторов, влияние которых оценивается с помощью плана 2**(6-0) (объяснение обозначения 2**(k-p) см. ниже). Результаты эксперимента показывают, что имеется три наиболее важных фактора: Полисульфидный индекс, Время и Температура (см. Бокс и Дрейпер (1987), стр. 116). Можно представить ожидаемое воздействие на интересующую нас переменную (в данном случае светостойкость окраски) в виде так называемой кубической диаграммы. Эта диаграмма показывает ожидаемую (предсказываемую) среднюю стойкость на верхних и нижних уровнях каждого из трех факторов.

Пример 1.1: Отсеивающие планы.
Пример 1.1: Отсеивающие планы.

В предыдущем примере производилось оценивание плана с 6-ю различными факторами. Не редки случаи, когда очень много (до ста) различных факторов потенциально важны в исследовании. Специальные планы (например, план Плакетта-Бермана или планы с применением матрицы Адамара, смотрите Плакетт-Берман (1946)), реализованные в модуле Планирование эксперимента, позволяют эффективно “просеять” большое число факторов, используя минимальное число наблюдений.


Например, вы можете спланировать и проанализировать эксперимент со 127 факторами, использующий всего 128 опытов, а затем оценить главный эффект каждого фактора, легко определив, таким образом, какие из факторов важны при изучении процесса.

Пример 2: Планы 3**3.
Пример 2: Планы 3**3.

В работе Монтгомери (Монтгомери (1976), стр. 204) описывается эксперимент по определению факторов, существенно влияющих на потери сиропа при изготовлении безалкогольных напитков, - потери возникают из-за вспенивания при наполнении 20-литровых металлических контейнеров. Рассматривались три фактора: (1) конфигурация заливного наконечника, (2) оператор машины по разливу и (3) давление, под которым производится разлив. Каждый фактор был установлен на трех различных уровнях, что определяет полный экспериментальный план 3**(3-0) (объяснение обозначения 3**(k-p) см. ниже).



Кроме того, для каждой комбинации факторов было проведено два измерения, таким образом, план 3**(3-0) был полностью повторен или, как говорят, реплицирован.

Пример 3: Максимизация выхода химической реакции.
Пример 3: Максимизация выхода химической реакции.

Выход продукта многих химических реакций зависит от времени и температуры. К сожалению, эти функции не линейны и не монотонны. Другими словами, нельзя сказать: “чем больше продолжительность реакции, тем больше выход” и “чем выше температура, тем больше выход”.



Формально цель эксперимента заключается в том, чтобы найти оптимальное положение на поверхности выхода, образованной двумя переменными: временем и температурой.

Пример 4: Проверка эффективности четырех топливных присадок.
Пример 4: Проверка эффективности четырех топливных присадок.

Планы на латинских квадратах обычно используются, когда интересующие нас факторы измеряются более чем на двух уровнях, а характер задачи подсказывает возможность разбиения плана на блоки. Например, представьте, что изучается 4 топливные присадки для снижения содержания в выхлопах окиси азота (смотрите монографию Бокса, Хантера и Хантера, 1978, стр. 263).


Вы имеете в своем распоряжении 4 водителя и 4 автомобиля. Вам не интересен эффект влияния работы водителей или типа автомобиля на снижение концентрации окиси азота, однако, вам не хотелось бы, что бы полученные результаты относились к некоторому конкретному водителю или автомобилю (из смещения по этим факторам). Планы на латинских квадратах позволяют оценить главные эффекты всех факторов несмещенным образом. В данном примере размещение уровней воздействия в виде латинского квадрата гарантирует, что различия между водителями и автомобилями не повлияют на оценку эффекта различных топливных присадок.

Пример 5: Улучшение поверхностной однородности при производстве кремниевых кристаллов.
Пример 5: Улучшение поверхностной однородности при производстве кремниевых кристаллов.

Производство надежных микропроцессоров требует высоко отлаженного производственного процесса. Отметим, что в данном примере одинаково, если не более важно, контролировать как изменчивость некоторых производственных характеристик, так и их средние значения. Например, средняя толщина поверхностного слоя поликремниевой подложки производственный процесс может быть отрегулирован превосходно, однако, если изменчивость этого параметра велика (представьте, что срез под микроскопом будет похож на ломанную линию с острыми углами), то микрочипы будут недостаточно надежными. Фадке (1989) описал, как различные характеристики производственного процесса (давление, температура кипящего слоя, давление обдувающего поток азота и т.д.) влияют на изменчивость толщины поверхностного слоя кремния на подложке. Не существует теоретической модели, которые позволяла бы инженеру предсказать, как эти факторы влияют на однородность поверхности кристаллов. Следовательно, для оптимизации производственного процесса нужно систематизировано проводить эксперименты на различных уровнях факторов. В этом случае чрезвычайно полезны так называемые Робастные планы Тагучи.

Пример 6: Планы для смесей.
Пример 6: Планы для смесей.

В работе Корнелла (1990, стр. 9) приводится пример типичной задачи анализа смесей.


Было проведено исследование для определения оптимального состава рыбного паштета как результата смешения различных пород рыб, идущих на его приготовление (в том числе кефаль, окунь и горбыль). В отличие от обычных экспериментов, в смеси общая сумма долей должна быть постоянна, например, равна 100%. Результаты таких экспериментов обычно представляются графически в виде тернарных графиков.



Основное ограничение - три компоненты в сумме равняются константе - выражается в треугольной форме графика.

Пример 6.1: Планы для смесей с ограничениями.
Пример 6.1: Планы для смесей с ограничениями.

В частности, в планах по изучению смесей на относительные доли компонентов можно наложить дополнительные ограничения (помимо условия постоянства их суммы). Например, предположим, что вы хотите разработать наилучший по вкусу фруктовый пунш, состоящий из смеси пяти фруктовых соков. Поскольку предполагается, что изготовленная смесь должна быть именно фруктовым пуншем, чистые смеси, состоящие только из одного фруктового сока не рассматриваются. Дополнительные ограничения на область допустимых смесей могут возникнуть из-за высокой стоимости одного из соков или по некоторым другим соображениям, поскольку некоторый конкретный сок не может иметь в смеси долю более чем, скажем, 30% (иначе фруктовый пунш был бы слишком дорог, длительность его хранения была бы невелика, пунш не мог бы производиться в больших количествах и так далее). Подобные поверхности с ограничениями представляют многочисленные трудности для практиков. Однако все они могут быть легко преодолены с помощью модуля Планирование эксперимента.



В общем случае, при заданных ограничениях ищется план эксперимента, который позволяет извлечь максимальное количество информации об интересующей нас функции отклика (например, о вкусе фруктового пунша) на выбранной многомерной поверхности. Вычислительные проблемы К основным видам задач, решаемых в модуле Планирование эксперимента, относятся: планирование оптимального эксперимента анализ результатов эксперимента. Для решения задач первого вида имеется несколько подходов, реализованных в соответствующих планах экспериментов, основную идею которых можно выразить следующим образом.


В общем случае, цель экспериментатора состоит в получении наиболее несмещенной (или наименее смещенной) оценки эффекта фактора вне зависимости от установок других факторов. Более точно, вы пытаетесь построить планы, в которых главные эффекты не смешаны друг с другом, а может быть даже и с взаимодействиями факторов. Компоненты дисперсии, синтез деноминатора
Вычислительные проблемы К основным видам задач, решаемых в модуле Планирование эксперимента, относятся: планирование оптимального эксперимента анализ результатов эксперимента. Для решения задач первого вида имеется несколько подходов, реализованных в соответствующих планах экспериментов, основную идею которых можно выразить следующим образом. В общем случае, цель экспериментатора состоит в получении наиболее несмещенной (или наименее смещенной) оценки эффекта фактора вне зависимости от установок других факторов. Более точно, вы пытаетесь построить планы, в которых главные эффекты не смешаны друг с другом, а может быть даже и с взаимодействиями факторов. Компоненты дисперсии, синтез деноминатора

Некоторые модули в STATISTICA позволяют проводить анализ планов со случайными эффектами (смотрите Методы дисперсионного анализа). Модуль Компоненты дисперсии и смешанная модель ANOVA/ANCOVA содержит различные опции для оценок компонент дисперсии для случайных эффектов, а также для проведения приближенных F - тестов, основанных на обобщенном члене ошибки. Смотрите также Методы дисперсионного анализа для знакомства с различными опциями ANOVA/ANCOVA, доступных в STATISTICA. Выводы
Выводы

Экспериментальные методы находят все большее применение в промышленности для оптимизации производственных процессов. Целью этих методов является поиск оптимальных уровней факторов, определяющих течение процесса производства. В рассмотренных примерах мы познакомили вас с основными типами планов, обычно используемыми в промышленности: планами 2**(k-p) (двухуровневыми многофакторными планами), отсеивающими планами для большего числа факторов, планами 3**(k-p) (трехуровневыми многофакторными планами), смешанными 2-х и 3-х уровневыми планами, центральными композиционными планами (или планами поверхности отклика), планами на латинских квадратах, робастными планами Тагучи, планами для смесей, а также специальными процедурами для проведения экспериментов на поверхностях с ограничениями.


Интересно, что многие из этих методов прошли путь от заводских цехов до кабинетов менеджеров и аналитиков, зарекомендовав себя в задачах планирование прибыли в бизнесе, управления финансовыми потоками в банковском деле и многих других (см., например, работу Йокиама и Тагучи (1975)).

Все эти методы подробно обсуждаются в следующих разделах: Дробные 2**(k-p) факторные планы Максимально несмешанные 2**(k-p) планы Планы 3**(k-p), планы Бокса-Бенкена и смешанные 2-х и 3-х уровневые планы Центральные композиционные планы и нефакторные планы поверхности отклика Планы на латинских квадратах Методы Тагучи: робастное планирование эксперимента Планы для смесей и тернарные поверхности Планы для поверхностей и смесей с ограничениями D- и A- опттимальные планы для поверхностей и смесей Дробные 2**(k-p) факторные планы

Основная идея
Основная идея

Во многих случаях достаточно рассмотреть всего два уровня факторов, влияющих на производственный процесс. Например, температура проведения химического процесса может быть установлена немного ниже или немного выше заданного уровня, количество растворителя при производстве красителя можно немного увеличить или уменьшить и так далее. Экспериментатор хотел бы установить, влияют ли какие-либо из этих изменений на результат производственного процесса. Наиболее очевидный подход в данном случае состоит в полном переборе комбинаций уровней интересующих факторов. Это отлично сработает, если бы число необходимых опытов в таком эксперименте не росло экспоненциально. Например, если вы хотите провести эксперимент с 7 факторами, то необходимое число опытов равно 2**7 = 128. Чтобы изучить 10 факторов вам потребуется 2**10 = 1,024 опытов. Поскольку для проведения каждого опыта нужна длительная и дорогостоящая перенастройка, то на практике часто нереально ставить столь большое число опытов. В этом случае при планировании эксперимента обычно используют дробные планы, отбрасывающие взаимодействия высокого порядка и уделяющие наибольшее внимание главным эффектам. Построение плана Подробное описание того, как строятся дробные факторные планы, выходит за пределы данного введения.


Много интересного о 2**(k-p) планах можно найти, например, в работах Бейна и Рубина (1986), Бокса и Дрейпера (1987), Бокса, Хантера и Хантера (1978), Даниела (1976), Деминга и Моргана (1993), Мейсона, Ганста и Гесса (1989), Райана (1989), а также Монтгомери (1991) и многих других. В общем случае, программа успешно использует взаимодействия наивысших порядков для генерации новых факторов. В качестве примера рассмотрим следующий план, включающий 11 факторов, но требующий проведения только 16 опытов (наблюдений).

Таблица 1
Таблица 1

Design: 2**(11-7), Resolution III Run A B C D E F G H I J K

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16	1 1 1 1 1 1 1 1 -1 -1 -1 -1 -1 -1 -1 -1	1 1 1 1 -1 -1 -1 -1 1 1 1 1 -1 -1 -1 -1	1 1 -1 -1 1 1 -1 -1 1 1 -1 -1 1 1 -1 -1	1 -1 1 -1 1 -1 1 -1 1 -1 1 -1 1 -1 1 -1	1 1 -1 -1 -1 -1 1 1 -1 -1 1 1 1 1 -1 -1	1 -1 -1 1 -1 1 1 -1 1 -1 -1 1 -1 1 1 -1	1 -1 -1 1 1 -1 -1 1 -1 1 1 -1 -1 1 1 -1	1 -1 1 -1 -1 1 -1 1 -1 1 -1 1 1 -1 1 -1	1 -1 -1 1 -1 1 1 -1 -1 1 1 -1 1 -1 -1 1	1 1 1 1 -1 -1 -1 -1 -1 -1 -1 -1 1 1 1 1	1 1 -1 -1 1 1 -1 -1 -1 -1 1 1 -1 -1 1 1

Чтение плана. План, представленный в таблице, интерпретируется следующим образом. Каждый столбец таблицы содержит +1 или -1 для обозначения уровня соответствующего фактора (верхнего или нижнего, соответственно). Так, например, в первом опыте эксперимента все факторы от A до K установлены на верхнем уровне (+1); во втором опыте факторы A, B, и C - на верхнем уровне, а фактор D - на нижнем и так далее. Отметим также, что имеется множество опций для отображения плана на экране и сохранения в файле с использованием обозначений, отличных от ± 1 для уровней факторов. Например, можно использовать реальные значения факторов (например, 90° C и 100° C) или текстовые метки (Низкая температура, Высокая температура).

Рандомизация опытов. Поскольку многие условия проведения эксперимента могут измениться от опыта к опыту то, чтобы не возникали систематические смещения, следует рандомизировать порядок проведения опытов (модуль Планирование эксперимента позволяет случайно выбрать порядок их проведения).




Разрешение плана
Разрешение плана

План в приведенной выше таблице описывается как 2**(11-7) план разрешения III (три). Это означает, что изучается k = 11 факторов (первая цифра в скобках), однако p = 7 из этих факторов (вторая цифра в скобках) порождены взаимодействиями полного факторного плана 2**[(11-7) = 4]. В результате план не обеспечивает полного разрешения, т.е. имеются эффекты взаимодействий, которые смешиваются с другими эффектами (идентичны им). Вообще, план называется планом разрешения R, если в нем ни одно взаимодействие порядка l = 1,…,[(r+1)/2] не смешивается с каким-либо взаимодействием порядка меньше R-l. В данном примере, R равно 3. Ни одно из взаимодействий порядка l = 1 (то есть ни один главный эффект) не смешивается здесь с каким-либо другим взаимодействием порядка меньше R-l = 3-1 = 2. Главные эффекты в этом плане смешиваются со взаимодействиями 2-го порядка и, следовательно, все взаимодействия более высоких порядков также смешаны. Если провести 64 опыта по плану 2**(11-5), полученное разрешение равнялось бы четырем (R = IV). Для того чтобы сделать такой вывод достаточно убедиться, что взаимодействия порядка (l=1) (главные эффекты) не смешиваются со взаимодействиями порядка меньше R-l = 4-1 = 3, а взаимодействия второго порядка (l=2) не смешиваются со взаимодействиями порядка меньшего, чем R-l = 4-2 = 2. Это приводит к тому, что некоторые взаимодействия второго порядка в данном плане смешаны друг с другом. Планы Плакетта - Бермана (матрица Адамара) для отсеивания
Планы Плакетта - Бермана (матрица Адамара) для отсеивания

Если необходимо просеять большое число факторов, которые могут быть потенциально важными (т. е. связаны с интересующей нас зависимой переменной), хотелось бы использовать план, который бы позволил тестировать наибольшее число главных эффектов при наименьшем числе наблюдений, то есть построить план разрешения III с наименьшим числом наблюдений. Один из способов планирования такого эксперимента состоит в смешивании всех взаимодействий с “новыми” главными эффектами.


Такие планы часто называют насыщенными, поскольку вся информация в них используется для оценки параметров, не оставляя степеней свободы для оценки эффекта (члена) ошибок ДА. Поскольку дополнительные факторы создаются приравниванием (“присвоением псевдонимов”, смотрите ниже) “новых факторов” к взаимодействиям в полной факторной модели, то эти планы всегда будут состоять из 2**k опытов, (то есть, 4, 8, 16, 32 и так далее опытов). Плакетт и Берман (Plackett и Burman, 1946) показали, как полная факторная модель может быть разбита так, чтобы получить насыщенные планы, в которых число опытов кратно 4, а не степени 2. Такие планы иногда называют планами с матрицей Адамара. Конечно, вы не обязаны использовать все имеющиеся факторы в этих планах, и фактически, иногда вам хотелось бы сгенерировать насыщенный план для еще одного фактора сверх тех, которые вы бы хотели тестировать. Это позволит оценить изменчивость случайных эффектов и тестировать оценки параметров на статистическую значимость.


Усиление разрешения плана методом инверсии
Усиление разрешения плана методом инверсии

Одним из способов, с помощью которых разрешение III плана может быть усилено до разрешения IV, является метод инверсии (например, смотрите Box и Draper, 1987, Deming и Morgan, 1993). Предположим, что имеется 7-факторный план с 8 опытами:

Таблица 2
Таблица 2

Design: 2**(7-4) design Run A B C D E F G

1 2 3 4 5 6 7 8	1 1 1 1 -1 -1 -1 -1	1 1 -1 -1 1 1 -1 -1	1 -1 1 -1 1 -1 1 -1	1 1 -1 -1 -1 -1 1 1	1 -1 1 -1 -1 1 -1 1	1 -1 -1 1 1 -1 -1 1	1 -1 -1 1 -1 1 1 -1

Это план с разрешением III, в нем 2-х факторные взаимодействия смешаны с главными эффектами. Вы можете преобразовать его в план разрешения IV с помощью опции Инверсия (усиление разрешения). При инверсии весь план копируется и добавляется в конец исходного плана с обращением всех знаков (заменой на противоположные):

Таблица 3
Таблица 3

Design: 2**(7-4) design (+Foldover)
Run  
A  
B  
C  
D  
E  
F  
G New:
H

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16	1 1 1 1 -1 -1 -1 -1 -1 -1 -1 -1 1 1 1 1	1 1 -1 -1 1 1 -1 -1 -1 -1 1 1 -1 -1 1 1	1 -1 1 -1 1 -1 1 -1 -1 1 -1 1 -1 1 -1 1	1 1 -1 -1 -1 -1 1 1 -1 -1 1 1 1 1 -1 -1	1 -1 1 -1 -1 1 -1 1 -1 1 -1 1 1 -1 1 -1	1 -1 -1 1 1 -1 -1 1 -1 1 1 -1 -1 1 1 -1	1 -1 -1 1 -1 1 1 -1 -1 1 1 -1 1 -1 -1 1	1 1 1 1 1 1 1 1 -1 -1 -1 -1 -1 -1 -1 -1

Исходный опыт номер 1 был -1, -1, -1, 1, 1, 1, -1; новый опыт номер 9 (первый опыт в “загнутой” порции) имеет все знаки, обратные знакам опыта 1: 1, 1, 1, -1, -1, -1, 1. Кроме того, для усиления разрешения плана добавочно получили 8-ой фактор (фактор H), который содержит все +1 для первых восьми опытов и –1 для загнутой порции нового плана. Заметим, что полученный план действительно является планом 2**(8-4) разрешения IV (смотрите также Box и Draper, 1987, стр. 160). Псевдонимы для взаимодействий: генераторы плана
Псевдонимы для взаимодействий: генераторы плана

Вернемся к плану разрешения R = III. Теперь вы знаете, что главные эффекты плана смешаны с взаимодействиями 2-го порядка, и можете поставить вопрос: “Какие взаимодействия и какие главные эффекты смешаны?” Модуль Планирование эксперимента генерирует следующую таблицу.

Таблица 4
Таблица 4


 
 
Factor Fractional Design Generators
2**(11-7) design
(Factors are denoted by numbers)
Alias

5   6   7   8   9 10 11	123   234   134   124 1234     12     13

Генераторы плана. Генераторы плана в таблице, являются “ключами”, показывающими, что факторы от 5 до 11 порождаются отождествлением их с конкретными   взаимодействиями первых 4 факторов в полном факторном плане 2**4. В частности, фактор 5 идентичен взаимодействию 123 (фактора 1, фактора 2 и фактора 3). Фактор 6 идентичен взаимодействию 234 и т. д. Помните, что план имеет разрешение III (три), и вы ожидаете, что некоторые главные эффекты смешаны с некоторыми взаимодействиями 2-го порядка: в самом деле, фактор 10 (десять) идентичен взаимодействию 12 (фактор 1 на фактор 2) и фактор 11 (одиннадцать) идентичен взаимодействию 13 (фактор 1 на фактор 3). Другой способ выражения этих тождеств состоит в высказывании, что главный эффект фактора 10 (десять) является псевдонимом взаимодействия факторов 1 и 2.



Подводя итоги, заметим, что коль скоро вы хотели бы включить меньше наблюдений (опытов) в ваш эксперимент, чем это требуется полным факторным планом 2**k, вы “жертвуете” эффектами взаимодействия и приписываете их некоторым уровням факторов. Получающийся план не является больше полным факторным, а становится дробным факторным.

Фундаментальное тождество.
Фундаментальное тождество.

Другой способ описания генератора плана состоит в простом уравнении. Именно, если, например, фактор 5 в дробном факторном плане идентичен взаимодействию 123 (фактор 1 и фактор 2 и фактор 3), тогда, умножая кодированные значения взаимодействия 123 на кодированные значения фактора 5, мы получим в результате +1 (если все уровни факторов закодированы +1) или:

I = 1235

где символ I заменяет +1 (используя стандартные обозначения как, например, в Box и Draper, 1987). Так, мы знаем, что фактор 1 смешан с взаимодействием 235 , фактор 2 смешан с взаимодействием 123 , а фактор 3 смешан с взаимодействием 125, поскольку в каждом случае их произведение должно равняться 1. Смешанность взаимодействий 2-го порядка также определяется этим уравнением, поскольку взаимодействие 12, будучи умножено на взаимодействие 35, должно дать в результате 1 и, следовательно, они идентичны или смешаны. Поэтому можно суммировать все смешанные в плане эффекты с помощью подобного тождества, называемого фундаментальным тождеством. Разбиение на блоки
Разбиение на блоки

В некоторых производственных процессах изделия производятся “партиями” или блоками. Вам хотелось бы быть уверенными в том, что эти блоки не сдвинут (не сместят) оценки главных эффектов. Например, вы имеете печь для обжига специальной керамики, однако ее размеры ограничены, так что вы не можете проводить все опыты сразу. В этом случае вы разбиваете эксперимент на блоки. Однако вы не хотели бы опыты с положительными установками факторов проводить в одном блоке, а с отрицательными – в другом. Иначе случайные отличия между блоками будут систематически воздействовать на оценки главных эффектов интересующих нас факторов (другими словами, сместят их).


В действительности вам хотелось бы так разбить опыты на блоки, чтобы любые различия между блоками (то есть блоковый фактор) не повлияли бы на результаты интересующих вас факторов. Это осуществляется введением блокового фактора как дополнительного фактора в плане эксперимента. Следовательно, вы “теряете” еще один эффект взаимодействия с блоковым фактором и получающийся план становится планом с меньшим разрешением. Однако такие планы часто имеют преимущество в мощности, т. к. позволяют оценивать и контролировать изменчивость производственного процесса, обусловленную различиями между блоками. Повторение плана
Повторение плана

Иногда желательно повторить (реплицировать) план, то есть провести опыт с каждой фиксированной комбинацией уровней факторов более одного раза. Это позволит оценить так называемую чистую ошибку эксперимента. Заметим, что при повторении плана можно вычислить изменчивость (изменчивость) измерений на каждой конкретной комбинации уровней факторов. Эта изменчивость даст представление о случайной ошибке измерений, (например, обусловленной неконтролируемыми факторами, ненадежностью инструментов измерений и так далее), поскольку повторные наблюдения совершаются при одинаковых условиях (установках уровней факторов). Такая оценка чистых ошибок может быть использована для оценки величины и статистической значимости вариации, обусловленной контролируемыми факторами.

Частные реплики. Если невозможно или нецелесообразно повторять все комбинации уровней (то есть проводить еще раз весь полный план), то можно все же получить оценку чистой ошибки при повторе только некоторых опытов. Однако нужно быть осторожным при рассмотрении смещений, потенциально возникающих при выборочном повторении только некоторых опытов. Если повторяются только те опыты, которые повторить легко, (например, собрать информацию в точках, где это дешевле всего), то можно случайно выбрать только те комбинации уровней факторов, в которых имеется очень маленькая (или очень большая) вариация, что приводит к недооценке (или переоценке) истинной величины чистой ошибки.


Таким образом, нужно тщательно рассматривать, обычно основываясь на вашем представлении об изучаемом процессе, какие опыты следует повторять, то есть какие опыты дадут хорошую (несмещенную) оценку чистой ошибки. Добавление центральных точек (центроидов)
Добавление центральных точек (центроидов)

Планирование эксперимента для факторов, установленных на двух уровнях неявно предполагает, что их воздействие на зависимую переменную (например, на прочность ткани) линейно. При этом невозможно проверить, имеется ли нелинейная компонента (например, квадратичная) в соотношении между фактором A и зависимой переменной, коль скоро A оценивается только в двух точках (например, нижнем и верхнем уровнях). Если предполагается, что соотношение между факторами и зависимой переменной, скорее всего, нелинейно, то необходим один или несколько опытов, где все (непрерывные) факторы установлены в промежуточных (средних) точках. Такие опыты принято называть опытами в центральных точках (или просто в центрах), поскольку они в некотором смысле находятся в центре плана (смотрите график).



Позднее при анализе (смотрите ниже) можно сравнить измерения зависимой переменной в центральной точке со средним в остальных точках плана. Это дает возможность проверить нелинейность зависимостей (смотрите Box и Draper, 1987): Если среднее зависимой переменной в центре плана значительно отличается от общего среднего по всем остальным точкам плана, то это является основанием считать, что простое предположение о линейности связи факторов с зависимой переменной не выполняется. Анализ результатов эксперимента 2**(k-p)
Анализ результатов эксперимента 2**(k-p)

Дисперсионный анализ.
Дисперсионный анализ.

Далее необходимо точно определить, какие факторы достоверно воздействуют на зависимую переменную. Например, в исследовании, приведенном Box и Draper (1987, стр. 115), хотелось бы знать, какие факторы, участвующие в производстве красителя, влияют на устойчивость краски. В этом примере, факторы 1 (Polysulfide – Полисульфид), 4 (Time – Время) и 6 (Temperature – Температура) значимо влияют на прочность ткани.


Влияние остальных факторов незначимо. Заметим, что для простоты в таблице, приведенной ниже, показаны только главные эффекты.

Таблица 5
Таблица 5

ANOVA; Var.:STRENGTH; R-sqr = .60614; Adj:.56469 (fabrico.sta) 2**(6-0) design; MS Residual = 3.62509
DV: STRENGTH   SS df MS F p (1)POLYSUFD
(2)REFLUX
(3)MOLES
(4)TIME
(5)SOLVENT
(6)TEMPERTR
Error
Total SS

48.8252 7.9102 .1702 142.5039 2.7639 115.8314 206.6302 524.6348	1 1 1 1 1 1 57 63	48.8252 7.9102 .1702 142.5039 2.7639 115.8314 3.6251	13.46867 2.18206 .04694 39.31044 .76244 31.95269	.000536 .145132 .829252 .000000 .386230 .000001

Чистая ошибка и потеря согласия. Если план эксперимента, по крайней мере, частично повторен (реплицирован), то можно оценить изменчивость ошибок эксперимента. Поскольку измерения сделаны при одинаковых условиях, то есть при идентичных установках уровней факторов, оценка вариабельности ошибок на основании этих опытов не зависит от того, является ли “истинная модель” линейной или нелинейной по природе или же включает взаимодействия высоких порядков. Так оцененная изменчивость ошибки представляет чистую ошибку, то есть ошибку, всецело обусловленную ненадежностью измерений зависимой переменной. Если оценка чистой ошибки получена, то ее можно использовать в критерии значимости для остаточной дисперсии, то есть остающейся изменчивости (вариабельности), которая не может быть обусловлена факторами и их взаимодействиями, присутствующими в текущей модели. Если на самом деле остаточная изменчивость значительно больше вариабельности чистой ошибки, можно сделать вывод, что остающаяся вариация обусловлена различием между группами и, следовательно, имеется потеря согласия модели с данными.

Таблица 6
Таблица 6

ANOVA; Var.:STRENGTH; R-sqr = .58547; Adj:.56475 (fabrico.sta) 2**(3-0) design; MS Pure Error = 3.594844
DV: STRENGTH   SS df MS F p (1)POLYSUFD
(2)TIME
(3)TEMPERTR
Lack of Fit
Pure Error
Total SS

48.8252 142.5039 115.8314 16.1631 201.3113 524.6348	1 1 1 4 56 63	48.8252 142.5039 115.8314 4.0408 3.5948	13.58200 39.64120 32.22154 1.12405	.000517 .000000 .000001 .354464

Например, таблица, приведенная выше, показывает результаты эксперимента для трех факторов, которые мы ранее идентифицировали, как наиболее важные по их воздействию на прочность краски (остальные факторы проигнорированы). Как видите в строке Lack of Fit – Потеря согласия, - остаточная вариация модели (после удаления трех главных эффектов) сравнима с чистыми ошибками, оцениваемыми из внутригрупповой вариации, - результирующее значение F-критерия не является статистически значимым. Следовательно, этот результат также подтверждает вывод, что, на самом деле, факторы Polysulfide - Полисульфид, Time – Время и Temperature – Температура достоверно влияют на окончательную прочность ткани аддитивным образом (без взаимодействий). Другими словами, все различия между средними, полученные в различных экспериментальных условиях, могут быть полностью объяснены простой аддитивной моделью с тремя переменными.

Параметры или оценки эффектов. Теперь посмотрим на то, как количественно факторы влияют на прочность окраски ткани.

Таблица 7
Таблица 7

Effect Std.Err. t (57) p Mean/Interc.
(1)POLYSUFD
(2)REFLUX
(3)MOLES
(4)TIME
(5)SOLVENT
(6)TEMPERTR

11.12344 1.74688 .70313 .10313 2.98438 -.41562 2.69062	.237996 .475992 .475992 .475992 .475992 .475992 .475992	46.73794 3.66997 1.47718 .21665 6.26980 -.87318 5.65267	.000000 .000536 .145132 .829252 .000000 .386230 .000001

Числа в этой таблице являются эффектами или оценками параметров. За исключением общего Mean/Intercept – Среднего/Свободного члена, эти оценки являются deviations – отклонениями среднего отрицательных установок от среднего положительных для каждого соответствующего фактора. Например, если вы измените установку фактора Time - Время с low – нижний на high - верхний, можете ожидать увеличение Strength – Прочности на 2.98; если вы установите значение фактора Polysulfd - Полисульфид на верхний уровень, то можете ожидать дальнейшее увеличение на 1.75 и так далее.

Как видите, те же самые три фактора, которые были статистически значимыми, показывают наивысшие оценки параметров; так что установки этих трех факторов наиболее важны для окончательной прочности ткани.



Для анализа, включающего взаимодействия, интерпретация параметров эффектов несколько более сложная. Параметры двухуровневых взаимодействий определяются как полуразность между главными эффектами одного фактора на двух уровнях второго фактора (смотрите Mason, Gunst и Hess, 1989, стр. 127); подобным же образом, параметры трехфакторных взаимодействий определяются как полуразности между эффектами двухфакторного взаимодействия на двух уровнях третьего фактора и так далее.

Регрессионные коэффициенты. Можно также взглянуть на параметры модели регрессии (смотрите Множественная регрессия, том I). Чтобы продолжить пример, рассмотрим следующее уравнение прогноза:

Strength = const + b1 *x1 +... + b6 *x6

Здесь x1 до x6 обозначают 6 анализируемых факторов. Таблица Effect Estimates - Оценки эффектов, показанная ранее, также содержит эти оценки параметров:

Таблица 8
Таблица 8

 
Coeff. Std.Err.
Coeff. -95.%
Cnf.Limt +95.%
Cnf.Limt Mean/Interc.
(1)POLYSUFD
(2)REFLUX
(3)MOLES
(4)TIME
(5)SOLVENT
(6)TEMPERTR

11.12344 .87344 .35156 .05156 1.49219 -.20781 1.34531	.237996 .237996 .237996 .237996 .237996 .237996 .237996	10.64686 .39686 -.12502 -.42502 1.01561 -.68439 .86873	11.60002 1.35002 .82814 .52814 1.96877 .26877 1.82189

На самом деле эти оценки содержат весьма мало “новой” информации, поскольку они просто равны половине значений параметров, показанных ранее (кроме оценок для Mean/Intercept - Среднего/Свободного члена). Это теперь приобретает новый смысл, если интерпретировать коэффициент как отклонение (зависимой переменной) при высокой установке соответствующего фактора от значения в центре. Заметим, однако, такая интерпретация верна только для случая, когда уровни факторов закодированы как -1 и +1, соответственно. Другими словами, кодировка факторов влияет на значения оценок параметров. В примере из монографии Box и Draper (1987, стр. 115), значения различных факторов измерялись в весьма разных шкалах:

Таблица 9
Таблица 9

data file: FABRICO.STA [ 64 cases with 9 variables ]
2**(6-0) Design, Box & Draper, p. 117   POLYSUFD REFLUX MOLES TIME SOLVENT TEMPERTR STRENGTH HUE BRIGTHNS 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
. . .

6 7 6 7 6 7 6 7 6 7 6 7 6 7 6 . . .	150 150 170 170 150 150 170 170 150 150 170 170 150 150 170 . . .	1.8 1.8 1.8 1.8 2.4 2.4 2.4 2.4 1.8 1.8 1.8 1.8 2.4 2.4 2.4 . . .	24 24 24 24 24 24 24 24 36 36 36 36 36 36 36 . . .	30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 . . .	120 120 120 120 120 120 120 120 120 120 120 120 120 120 120 . . .	3.4   9.7   7.4 10.6   6.5   7.9 10.3   9.5 14.3 10.5   7.8 17.2   9.4 12.1   9.5 . . .	15.0   5.0 23.0   8.0 20.0   9.0 13.0   5.0 23.0   1.0 11.0   5.0 15.0   8.0 15.0 . . .	36.0 35.0 37.0 34.0 30.0 32.0 28.0 38.0 40.0 32.0 32.0 28.0 34.0 26.0 30.0 . . .

Ниже показаны оценки коэффициентов регрессии, базирующиеся на незакодированных исходных значениях факторов:

Таблица 10
Таблица 10

Regressn
Coeff.  
Std.Err.  
t (57)  
p Mean/Interc.
(1)POLYSUFD
(2)REFLUX
(3)MOLES
(4)TIME
(5)SOLVENT
(6)TEMPERTR

-46.0641 1.7469 .0352 .1719 .2487 -.0346 .2691	8.109341 .475992 .023800 .793320 .039666 .039666 .047599	-5.68037 3.66997 1.47718 .21665 6.26980 -.87318 5.65267	.000000 .000536 .145132 .829252 .000000 .386230 .000001

Поскольку метрики для различных факторов не сопоставимы, то несопоставимы значения коэффициентов регрессии. Именно поэтому полезнее взглянуть на оценки параметров ДА (для закодированных значений уровней факторов), как это и было представлено ранее. Однако коэффициенты регрессии могут быть полезны, когда нужно предсказать зависимую переменную, основываясь на исходной метрике факторов.


Графические опции
Графические опции

Графики остатков.
Графики остатков.

Вначале перед принятием конкретной “модели”, включающей конкретное число эффектов (например, главные эффекты для Polysulfide - Полисульфида, Time – Времени и Temperature – Температуры в текущем примере), нужно всегда проверить распределение величин остатков, которые вычисляются как разница между модельными (вычисленными на построенной модели) и наблюдаемыми значениями. Предоставляются опции для вычисления гистограмм таких остатков, а также для вероятностных графиков.



Оценки параметров и таблицы ДА основаны на предположении нормальности распределения остатков (смотрите Элементарные понятия). Гистограмма представляет способ визуально проверить это предположение. Так называемый нормальный вероятностный график является другим общим средством оценки того, сколь хорошо наблюдаемые значения (в нашем случае - остатков) согласуются с теоретическим распределением. На графике наблюдаемые значения остатков отмечаются на горизонтальной оси X; вертикальная ось Y отмечает ожидаемые нормальные значения для соответствующих величин после их упорядочения по возрастанию.


Если все значения укладываются на прямую (как это продемонстрировано на вышеприведенной иллюстрации), можно быть удовлетворенным тем, что остатки следуют нормальному распределению.

Диаграмма Парето эффектов. Диаграмма Парето является действенным средством для демонстрации результатов эксперимента непрофессионалам (в частности, начальству).



На этой диаграмме оценки эффектов ДА расположены по абсолютной величине значений: от наибольших к наименьшим. Величина каждого эффекта представлена столбиком, и часто столбики пересекают линией, указывающей, каков должен быть эффект по величине (то есть какова должна быть длина столбика), чтобы быть статистически значимым.

Нормальный график эффектов. Другим полезным, хотя и технически более сложным графиком, является нормальный вероятностный график. Как и в нормальной вероятностной диаграмме остатков, вначале оценки эффектов упорядочиваются по возрастанию, а затем вычисляются нормальные значения z, основываясь на предположении, что оценки распределены нормально. Эти значения z отмечаются на оси Y, а наблюдаемые оценки наносятся на оси X (как показано ниже).



Квадратичные и кубические диаграммы. Эти диаграммы часто используются для итогового представления предсказываемых значений зависимой переменной для соответствующих верхних и нижних установок факторов. Квадратичная диаграмма показывает предсказываемые значения (и по желанию доверительные интервалы) для двух факторов одновременно. Кубическая диаграмма показывает предсказываемые значения (и по желанию доверительные интервалы) для трех факторов одновременно.



Диаграммы взаимодействий. Общим видом диаграммы для демонстрации средних является стандартная диаграмма взаимодействий, на которой средние показаны точками, соединенными линиями. Такая диаграмма полезна, когда в модели присутствуют эффекты взаимодействий.



Контурные диаграммы и диаграммы поверхности. Если факторы плана непрерывны по своей природе, то часто также полезно взглянуть на диаграмму поверхности или контурную диаграмму зависимой переменной как функции факторов.





Типы таких диаграмм будут обсуждены позднее в данном разделе в связи с планами 3**(k-p), а также центральными композиционными планами и планами поверхности отклика. Выводы
Выводы

Планы 2**(k-p) наиболее часто используются в промышленности. Вклад большого числа факторов в производственный процесс может быть оценен относительно эффективно (т.е. с помощью небольшего числа опытов). Логика экспериментов такого рода весьма проста (каждый фактор имеет только два уровня), а с помощью модуля Планирование эксперимента построение плана и анализ таких экспериментов занимают буквально секунды.

Недостатки.
Недостатки.

Простота этих планов является их главным недостатком. Как было отмечено ранее, основанием для использования двухуровневых факторов является убеждение в том, что изменения зависимой переменной (например, прочности ткани) линейны по своей природе. Часто это не выполняется, то есть многие переменные связаны с характеристиками качества нелинейным образом. В приведенном выше примере, если бы вы непрерывно увеличивали фактор температуры (существенно связанный с прочностью окраски ткани), то в конечном счете обнаружили бы “пик”, после которого прочность убывает при возрастании температуры. Этот тип нелинейности может быть обнаружен, если план содержит центральную точку. Нельзя точно подогнать нелинейную модель (например, квадратичную) с помощью планов 2**(k-p), однако, это можно сделать с помощью центральных композиционных планов.

Другим недостатком дробных планов является предположение о том, что взаимодействия высоких порядков отсутствуют, но иногда они действительно присутствуют. Например, если некоторые другие факторы установлены так, что оказывают отрицательное влияние на температуру. Однако в дробных факторных планах взаимодействия высоких порядков (выше двух), как правило, не будут обнаружены.

В начало

Максимально несмешанные 2**(k-p) планы

Основная идея
Основная идея

Дробные 2**(k-p) факторные планы часто используются в промышленных экспериментах, так как позволяют сокращать количество используемых данных.


Предположим в качестве примера, что инженеру нужно изучить эффект воздействия на производственный процесс 11 переменных факторов, каждый из которых может быть установлен на 2 уровнях. Обозначим число факторов через k, в нашем примере это 11. Эксперимент с полным факторным планом, когда изучаются эффекты каждой комбинации уровней каждого фактора, будет требовать проведения 2**(k) опытов, или 2048 в нашем случае. Для уменьшения объема работ с данными инженер может решить отказаться от рассмотрения эффектов взаимодействий высоких порядков 11 факторов, и вместо этого сосредоточиться только на выявлении главных эффектов 11 факторов и некоторых эффектов взаимодействий низкого порядка, которые могут быть оценены с помощью эксперимента с меньшим, более разумным числом опытов. Существует другая, более теоретическая причина отказа от больших полных факторных 2-х уровневых экспериментов. Обычно нелогично заниматься идентификацией эффектов взаимодействий факторов эксперимента высоких порядков, игнорируя нелинейные эффекты низкого порядка, такие как квадратичные и кубические эффекты, которые не могут быть оценены, если используются только 2-х уровневые факторы. Таким образом, несмотря на то, что практические соображения часто приводят к необходимости экспериментов с малым числом опытов, это логически оправданно для таких экспериментов.

Альтернативой полного 2**k факторного плана является 2**(k-p) дробный факторный план, который требует только "часть" данных, необходимых для полного факторного плана. В нашем примере с k=11 факторами, если могут быть проведены только 64 опыта, может быть построен 2**(11-5) дробный факторный план для эксперимента с 2**6 = 64 опытами. В сущности, построен полный k - p = 6 факторный план эксперимента с уровнями p факторов, "построенных" по уровням выбранных взаимодействий высокого порядка других 6 факторов. Дробные факторные "жертвуют" эффектами взаимодействий высокого порядка, но эффекты низкого порядка, могут еще быть вычислены корректно.


Однако могут быть использованы различные критерии для выбора взаимодействий высокого порядка, используемых в качестве генераторов, среди которых некоторые критерии иногда приводят к различным "лучшим" планам.

Дробные 2**(k-p) факторные планы могут также содержать блоковые факторы. В некоторых производственных процессах изделия выпускаются "партиями" или блоками. Для того чтобы быть уверенным, что эти блоки не смещают ваши оценки эффектов k factors, блоковые факторы могут быть добавлены в план как дополнительные. Следовательно, вы можете "пожертвовать" дополнительными эффектами взаимодействий для создания блоковых факторов, но эти планы часто имеют большую мощность, т.к. позволяют оценивать и контролировать вариабельность (изменчивость) производственного процесса, вызванную блоковыми различиями. Критерий плана
Критерий плана

Многие концепции, которые обсуждались в этом обзоре, также относятся и к разделу Обзор дробных 2**(k-p) факторных планов. Однако техническое описание построения дробных факторных планов выходит за рамки Вводного обзора. Детальные объяснения, как план 2**(k-p) эксперимента может быть найден, содержатся, например, у Bayne и Rubin (1986), Box и Draper (1987), Box, Hunter, и Hunter (1978), Montgomery (1991), Daniel (1976), Deming и Morgan (1993), Mason, Gunst, и Hess (1989), или Ryan (1989), и существует много других книг по этому предмету.

Обычно опция Максимально несмешанные 2**(k-p) планы будет производить последовательный отбор, в зависимости от выбранного критерия поиска, с взаимодействиями высшего порядка в качестве генераторов для p факторов. Для примера рассмотрим следующий план, который включает 11 факторов, но требует только 16 опытов (наблюдений).

Таблица 11
Таблица 11

Design: 2**(11-7), Resolution III Run A B C D E F G H I J K

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16	1 1 1 1 1 1 1 1 -1 -1 -1 -1 -1 -1 -1 -1	1 1 1 1 -1 -1 -1 -1 1 1 1 1 -1 -1 -1 -1	1 1 -1 -1 1 1 -1 -1 1 1 -1 -1 1 1 -1 -1	1 -1 1 -1 1 -1 1 -1 1 -1 1 -1 1 -1 1 -1	1 1 -1 -1 -1 -1 1 1 -1 -1 1 1 1 1 -1 -1	1 -1 -1 1 -1 1 1 -1 1 -1 -1 1 -1 1 1 -1	1 -1 -1 1 1 -1 -1 1 -1 1 1 -1 -1 1 1 -1	1 -1 1 -1 -1 1 -1 1 -1 1 -1 1 1 -1 1 -1	1 -1 -1 1 -1 1 1 -1 -1 1 1 -1 1 -1 -1 1	1 1 1 1 -1 -1 -1 -1 -1 -1 -1 -1 1 1 1 1	1 1 -1 -1 1 1 -1 -1 -1 -1 1 1 -1 -1 1 1

Интерпретация плана. План, показанный в таблице результатов, может интерпретироваться следующим образом. Каждый столбец содержит +1 или -1 для обозначения уровня соответствующего фактора (верхнего или нижнего, максимального или минимального). Так в первом опыте все факторы от A до K установлены на верхнем уровне, во втором опыте факторы A, B и C установлены на верхнем уровне, а фактор D – на нижнем уровне, и так далее. Заметим, что установки фактора E для каждого опыта эксперимента могут быть получены как произведение соответствующих установок факторов A, B и C. Следовательно, в этом плане эффект взаимодействия A x B x C не может быть оценен независимо от эффекта фактора E так как эти два эффекта смешаны. Точно так же установки фактора F могут быть получены как произведение соответствующих установок факторов B, C и D. Согласно терминологии, ABC и BCD являются генераторами факторов E и F, соответственно.

Критерий максимального разрешения плана.
Критерий максимального разрешения плана.

План, показанный в таблице результатов, характеризуется как 2**(11-7) план разрешения III (три). Это означает, что вы исследуете всего k = 11 факторов, но p = 7 из них сгенерированы взаимодействиями полного 2**[(11-7) = 4] факторного плана. В результате этот план не дает полного разрешения, то есть существуют некоторые эффекты взаимодействий, смешанные с другими эффектами. В общем случае план имеет разрешение R, когда в нем нет взаимодействий порядка l, смешанных с любыми другими взаимодействиями порядка, меньшего R - l. В нашем примере R равно 3. Здесь нет взаимодействий порядка l = 1 (т.е. главных эффектов), смешанных с любыми другими взаимодействиями порядка меньшего, чем R - l = 3 -1 = 2. Поэтому главные эффекты в этом плане не смешаны друг с другом, но смешаны с двухфакторными взаимодействиями, а следовательно, и с другими взаимодействиями более высокого порядка. Очевидным, но тем не менее очень важным общим критерием плана является то, что взаимодействия высшего порядка, используемые как генераторы, должны быть выбраны так, чтобы план имел максимально возможное разрешение.



Критерий максимальной несмешанности плана. Максимизация разрешения плана, однако, сама по себе не гарантирует, что выбранные генераторы дают "лучший" план. Для примера рассмотрим два различных плана с разрешением IV. В обоих планах главные эффекты могут быть несмешанными друг с другом, и 2-х факторные взаимодействия могут быть несмешанными с главными эффектами, т.е не существует взаимодействий порядка l = 2, смешанных с любыми другими взаимодействиями порядка меньшего, чем R - l = 4 - 2 = 2. Оба плана могли быть различными, однако, по отношению к степени смешивания 2-факторных взаимодействий. Для планов с разрешением IV "критическим порядком", при котором появляется смешивание эффектов, является 2-факторные взаимодействия. В одном плане не "критического порядка" 2-факторные взаимодействия могут быть несмешанными со всеми другими 2-факторными взаимодействиями, в то время как в другом плане фактически все 2-факторные взаимодействия могут быть несмешанными со всеми другими 2-факторными взаимодействиями. Второй план – это план "почти разрешения V" может быть более предпочтительнее, чем план "просто точно разрешения IV". Это означает, что даже несмотря на то, что главным критерием являлся критерий максимального разрешения, может быть введен дополнительный критерий, по которому выбираются те генераторы, содержащие максимальное число взаимодействий порядка меньшего или равного критическому, для данного разрешения, несмешанных со всеми другими взаимодействиями критического порядка. Этот критерий называется критерием максимальной несмешанности, иначе говоря, дополнительным критерием плана при поиске 2**(k-p) плана.

Критерий минимальной аберрации плана. Критерий минимальной аберрации плана является другим необязательным критерием, используемым при поиске 2**(k-p) плана. В некоторых отношениях этот критерий похож на критерий максимальной несмешанности. Формально план с минимальной аберрацией определяется как план с максимальным разрешением "с минимальным числом слов в определяющем взаимоотношении, которое имеет минимальную длину" (Fries & Hunter, 1984).


Менее формально, действие критерия основано на выборе генераторов, которые дают наименьшее число пар смешанных взаимодействий критического порядка. Например, план разрешения IV с минимальной аберрацией имел бы минимальное число пар смешанных 2-факторных взаимодействий.

Для пояснения различия между критериями максимальной несмешанности и минимальной аберрации рассмотрим максимально несмешанный план 2**(9-4) и план 2**(9-4) с минимальной аберрацией, как в примере, данном Box, Hunter, и Hunter (1978). Если вы сравните эти два плана, вы увидите, что в максимально несмешанном плане 15 из 36 2-факторных взаимодействий не смешаны с любыми другими 2-факторными взаимодействиями, в то время как в плане с минимальной аберрацией только 8 из 36 2-факторных взаимодействий не смешаны с любыми другими 2-факторными взаимодействиями. План с минимальной аберрацией, однако, дает 18 пар смешанных взаимодействий, в то время как максимально несмешанный план дает 21 пару смешанных взаимодействий. Таким образом, эти критерии приводят к выделению генераторов, дающих различные "лучшие" планы.

К счастью, выбор между критерием максимальной несмешанности и критерием минимальной аберрации не вносит различия в выбранном плане (за исключением, возможно, переобозначения факторов), когда имеется 11 или меньше факторов, - единственное исключение составляет план 2**(9-4), описанный выше (смотрите Chen, Sun, & Wu, 1993). Для планов с более чем 11 факторами оба критерия приводят к весьма различным планам, и нет лучшего совета, как использовать оба критерия, а затем сравнить полученные планы и выбрать план, наиболее отвечающий вашим потребностям. Добавим, что максимизация числа полностью несмешанных эффектов часто имеет больший смысл, чем минимизация числа пар смешанных эффектов. Выводы
Выводы

Дробные 2**(k-p) факторные планы, вероятно, наиболее часто используемые планы в промышленных экспериментах. Предмет рассмотрения любого 2**(k-p) дробного факторного эксперимента включает число исследуемых факторов, число опытов в эксперименте и наличие блоков опытов эксперимента.


После этих основных вопросов следует также определить, позволяет ли число опытов найти план требуемого разрешения и степень смешивания для критического порядка взаимодействий, для данного разрешения.

В начало

Планы 3**(k-p), планы Бокса-Бенкена и смешанные 2-х и 3-х уровневые планы

Обзор
Обзор

В некоторых случаях приходиться анализировать факторы, имеющие более 2-х уровней. Например, если предполагается, что влияние факторов на зависимую переменную не линейное, то необходимо, как говорилось ранее (см. 2**(k-p) планы), по меньшей мере, 3 уровня для проверки линейных и квадратичных эффектов (и взаимодействий). Более того, некоторые факторы могут быть категориальными с более чем двумя категориями. Например, вы можете иметь три различных машины, производящие конкретную деталь. Планирование экспериментов 3**(k-p)
Планирование экспериментов 3**(k-p)

Общий механизм построения дробных факторных планов на трех уровнях (планов 3**(k-p)) очень схож с тем, который описан для 2**(k-p) планов. Именно, отправляясь от полного факторного плана, взаимодействия используются для построения “новых” факторов (или блоков) с помощью определения их уровней равными соответствующим членам взаимодействий (то есть, определяя новые факторы как псевдонимы взаимодействий). Например, рассмотрим следующий простой факторный план 3**(3-1):

Таблица 12
Таблица 12

3**(3-1) fractional factorial
design, 1 block , 9 runs Standard
Run
A  
B  
C

1 2 3 4 5 6 7 8 9	0 0 0 1 1 1 2 2 2	0 1 2 0 1 2 0 1 2	0 2 1 2 1 0 1 0 2

Как и в случае планов 2**(k-p), план строится из полного факторного плана 3-1=2, чьи факторы перечислены в первых двух столбцах таблицы (факторы A и B). Фактор C строится на основании взаимодействия AB первых двух факторов. Значения фактора C вычисляются по формуле

C = 3 - mod3 (A+B)

Здесь символ mod3(x) обозначает сравнение по модулю 3 (остаток от деления x на 3). Например, mod3(0) равен 0, mod3(1) равен 1, mod3(3) равен 0, mod3(5) равен 2 (3 – наибольшее число, не большее 5, делящееся на 3; так что окончательно, 5-3=2) и так далее.



Фундаментальное тождество. Если вы примените эту функцию к сумме столбцов A и B в таблице, показанной выше, вы получите третий столбец C. Аналогично планам 2**(k-p) (см. 2**(k-p) планы для обсуждения понятия фундаментальное тождество в связи с планами 2**(k-p)), это смешивание взаимодействий с “новыми” главными эффектами может быть представлено выражением:

0 = mod3 (A+B+C)

Если вы снова взгляните на таблицу плана 3**(3-1), показанную ранее, вы увидите, что, на самом деле, если вы просуммируете числа в трех столбцах, они дадут в результате 0, 3 или 6, то есть значения, делящиеся на 3 без остатка (и, следовательно, mod3(A+B+C)=0). Или кратко ABC=0, для окончательного выражения смешивания факторов в дробном плане 3**(k-p).

Некоторые из планов будут иметь фундаментальные тождества, содержащие множитель 2, например,

0 = mod3 (B+C*2+D+E*2+F)

Это обозначение можно интерпретировать, как и прежде, то есть оператор деления по модулю3 для суммы B+2*C+D+2*E+F должен быть равен 0. Следующий пример демонстрирует данное тождество. Пример плана 3**(4-1) в 9 блоках Здесь приведены результаты для 4-х факторного 3-х уровневого дробного факторного плана в 9 блоках, требующего только 27 опытов.
Пример плана 3**(4-1) в 9 блоках Здесь приведены результаты для 4-х факторного 3-х уровневого дробного факторного плана в 9 блоках, требующего только 27 опытов.

SUMMARY: 3**(4-1) fractional factorial
Design generators: ABCD
Block generators: AB,AC2
Number of factors (independent variables): 4
Number of runs (cases, experiments): 27
Number of blocks: 9

Этот план позволит тестировать линейные и квадратичные эффекты 4 факторов в 27 опытах, собранных в 9 блоков по 3 наблюдения в каждом. Фундаментальное тождество или генератор плана ABCD, так что сумма по модулю 3 уровней факторов по всем четырем факторам равна 0. Фундаментальное тождество также позволяет определить смешивание факторов и взаимодействий плана (смотрите McLean и Anderson, 1984, для более подробного изложения).

Таблица 13


Таблица 13

Unconfounded Effects (experi3.sta) EXPERIM.
DESIGN List of uncorrelated factors and interactions
3**(4-1) fractional factorial design, 9 blocks, 27 runs Unconf. Effects
(excl. blocks) Unconfounded if
blocks included? 1
2
3
4
5
6
7
8

(1)A(L)      A    (Q) (2)B     (L)      B    (Q) (3)C     (L)      C    (Q) (4)D     (L)      D    (Q)	Yes Yes Yes Yes Yes Yes Yes Yes

Как вы видите, в этом плане 3**(4-1) главные факторы не смешаны друг с другом, несмотря на то, что эксперимент состоит из 9 блоков. Планы Бокса-Бенкена Для планов 2**(k-p) Plackett и Burman (1946) разработали метод для отсеивания максимального числа (главных) эффектов при возможно меньшем числе опытов. Эквивалентом для планов 3**(k-p) являются так называемые планы Бокса-Бенкена (Box и Behnken, 1960; смотрите также Box и Draper, 1984). Эти планы не имеют простых генераторов (конструируются комбинированием двухуровневых факторных планов с планами неполных блоков) и имеют сложную смесь взаимодействий. Тем не менее, они экономичны, и, следовательно, особенно полезны в случаях, когда дорого проводить необходимые опыты.
Планы Бокса-Бенкена Для планов 2**(k-p) Plackett и Burman (1946) разработали метод для отсеивания максимального числа (главных) эффектов при возможно меньшем числе опытов. Эквивалентом для планов 3**(k-p) являются так называемые планы Бокса-Бенкена (Box и Behnken, 1960; смотрите также Box и Draper, 1984). Эти планы не имеют простых генераторов (конструируются комбинированием двухуровневых факторных планов с планами неполных блоков) и имеют сложную смесь взаимодействий. Тем не менее, они экономичны, и, следовательно, особенно полезны в случаях, когда дорого проводить необходимые опыты.

Анализ плана 3**(k-p)


Анализ плана 3**(k-p)

Анализ таких типов планов происходит, в основном, таким же образом, как и анализ, описанный для планов 2**(k-p) планы. Однако для каждого эффекта теперь можно тестировать его линейность или квадратичность (нелинейность). Например, при изучении выхода химического процесса, температура может влиять на него нелинейным образом, то есть максимум выхода достигается при температуре, установленной на среднем уровне. Так, нелинейность часто возникает, если процесс находится вблизи оптимального уровня.


Дисперсионный анализ
Дисперсионный анализ

Чтобы оценить параметры ДА, уровни факторов, находящихся в анализе, специально перекодированы так, чтобы можно было тестировать линейные и квадратичные компоненты соотношений между факторами и зависимой переменной. Так, независимо от исходной метрики установки факторов (например, 100° C, 110° C, 120° C), программа всегда перекодирует эти значения в -1, 0, и +1 для вычислений. Получающиеся оценки параметров ДА могут интерпретироваться аналогично оценкам параметров планов 2**(k-p). Например, рассмотрим следующую таблицу результатов ДА:

Таблица 14
Таблица 14

Factor Effect Std.Err. t (69) p Mean/Interc.
BLOCKS(1)
BLOCKS(2)
(1)TEMPERAT (L)
TEMPERAT(Q)
(2)TIME (L)
TIME     (Q)
(3)SPEED (L)
SPEED     (Q)
     1L by 2L
     1L by 2Q
     1Q by 2L
     1Q by 2Q

103.6942 .8028 -1.2307 -.3245 -.5111 .0017 .0045 -10.3073 -3.7915 3.9256 .4384 .4747 -2.7499	.390591 1.360542 1.291511 .977778 .809946 .977778 .809946 .977778 .809946 1.540235 1.371941 1.371941 .995575	265.4805 .5901 -.9529 -.3319 -.6311 .0018 .0056 -10.5415 -4.6812 2.5487 .3195 .3460 -2.7621	0.000000 .557055 .343952 .740991 .530091 .998589 .995541 .000000 .000014 .013041 .750297 .730403 .007353

Оценки главных эффектов. По умолчанию оценки Эффектов для линейных эффектов (помеченных буквой L вслед за именем фактора) могут интерпретироваться как разница между средним откликом на высоких и низких установках соответствующих факторов.


Оценка квадратичного (нелинейного) эффекта ( помеченного буквой Q) может интерпретироваться как разница между средним откликом в центре (средней точке) и комбинацией отклика для высоких и низких установок соответствующего фактора.

Оценки эффектов взаимодействий. Как и для планов 2**(k-p), эффект линейно-линейного взаимодействия может интерпретироваться как половина разницы между линейным главным эффектом одного фактора на высоких и низких уровнях другого фактора. Аналогично, взаимодействия квадратичных компонент могут интерпретироваться как половина различия между квадратичным эффектом одного фактора на соответствующих установках другого (квадратично-линейное взаимодействие) или комбинации отклика на средних, высоких и низких установках (квадратично-квадратичное взаимодействие).

На практике, а также с точки зрения “интерпретируемости результатов” обычно пытаются избежать квадратичных взаимодействий. Например, квадратично-квадратичное взаимодействие факторов A и B указывает на то, что нелинейные эффекты фактора A изменяются нелинейным образом (модифицируются) при установках фактора B. Это означает, что имеется довольно сложное взаимодействие факторов, так что становится трудно понять и оптимизировать процесс. Иногда проблему можно решить с помощью подходящего нелинейного преобразования (например, логарифмирования log) зависимой переменной.

Центрированные и нецентрированные полиномы.
Центрированные и нецентрированные полиномы.

Как уже упоминалось ранее, простая интерпретация оценок эффектов применима только в случае, если использовалась параметризация модели по умолчанию. В этом случае программа кодирует квадратичные взаимодействия факторов так, чтобы они становились максимально “несвязанными” с линейными главными эффектами. Графическое представление результатов
Графическое представление результатов

Имеются те же диаграммы (например, диаграммы остатков) для планов 3**(k-p), что и для 2**(k-p) планов. Таким образом, перед интерпретацией окончательных результатов следует всегда вначале посмотреть на распределение остатков модели.


Заметим, что ДА предполагает нормальное распределение остатков (ошибок).

Диаграммы взаимодействия средних.
Диаграммы взаимодействия средних.

Если взаимодействуют категориальные факторы (например, тип машины, оператор или регулировка), то наилучший способ понять взаимодействия - просмотреть диаграммы маргинальных средних для взаимодействий.



Диаграмма поверхности. Если взаимодействующие факторы непрерывны, то следует посмотреть на диаграмму поверхности отклика, соответствующую подогнанной модели. Заметим, что данный график отражает уравнение прогноза, которое дает соответствующую поверхность отклика. Планы для факторов на 2-х и 3-х уровнях
Планы для факторов на 2-х и 3-х уровнях

Вы можете также генерировать стандартные планы для факторов на 2-х и 3-х уровнях. Точнее, вы можете создавать стандартные планы, перечисленные Кантором и Янгом для Национального бюро стандартов США (смотрите McLean и Anderson, 1984). Детали используемого метода построения плана лежат за пределами этого введения. В некотором смысле, техника является комбинацией процедур, описанных для планов 2**(k-p) и 3**(k-p). Следует отметить, что хотя все эти планы очень эффективны, они не обязательно ортогональны. Модуль Планирование эксперимента использует общий алгоритм оценки параметров ДА и сумм квадратов, который не требует ортогональности плана.

Планирование и анализ таких экспериментов лежит в русле обсуждений для экспериментов 2**(k-p) планов и 3**(k-p).

В начало

Центральные композиционные планы и нефакторные планы для поверхности отклика

Обзор
Обзор

Планы 2**(k-p) и 3**(k-p) требуют, чтобы факторы устанавливались, например, на 2-х или 3-х уровнях. Во многих примерах такие планы невозможны в силу неосуществимости некоторых комбинаций факторов по тем или иным причинам (например, когда факторы A и B не могут быть установлены на верхних уровнях одновременно). Помимо этого, по причинам, связанным с эффективностью, которые будут кратко обсуждены далее, часто желательно исследовать интересующую нас экспериментальную область в конкретных точках, которые не могут быть представлены в факторном плане. Все планы, обсуждаемые в данном разделе, посвящены оценке (подгонке) поверхностей отклика, удовлетворяющих общему уравнению (модели):



y = b0 +b1 *x1 +...+bk *xk + b12 *x1 *x2 +b13 *x1 *x3 +...+bk-1,k *xk-1 *xk + b11 *x1? +...+bkk *xk?

Иными словами, подгоняется модель для наблюдаемых значений зависимой переменной y, которая включает (1) главные эффекты факторов x1 , ..., xk, (2) их взаимодействия (x1*x2, x1*x3, ... ,xk-1*xk) и (3) их квадратичные компоненты (x1**2, ..., xk**2). Не делается никаких предположений относительно “уровней” факторов; вы можете анализировать любой набор непрерывных значений факторов.

Имеются некоторые соображения, касающиеся эффективности и несмещенности плана, которые приводят к стандартным планам, обычно используемым для подгонки поверхностей отклика, и эти стандартные планы будут коротко обсуждены (например, смотрите Box, Hunter и Hunter, 1978; Box и Draper, 1987; Khuri и Cornell, 1987; Mason, Gunst и Hess, 1989; Montgomery, 1991). Однако, как будет показано ниже при рассмотрении планов для поверхностей с ограничениями, а также D- и A-оптимальных планов, иногда эти стандартные планы не могут быть использованы по практическим соображениям. Повторим, однако, что опции анализа центральных композиционных планов не требуют никаких предположений относительно структуры массива данных, то есть относительно числа различных значений фактора или их комбинаций по опытам эксперимента и, следовательно, эти опции могут использоваться для анализа любого типа плана для подгонки к данным общей модели, описанной выше. Соображения относительно плана
Соображения относительно плана



Ортогональные планы.
Ортогональные планы.

Одной желательной характеристикой любого плана является независимость оценок главных эффектов и взаимодействий интересующих нас факторов. Например, предположим, что вы имеете двухфакторные эксперименты с факторами на двух уровнях. Ваш план состоит из четырех опытов:

Таблица 15
Таблица 15

A B Run 1
Run 2
Run 3
Run 4

1 1 -1 -1	1 1 -1 -1

В двух первых опытах оба фактора A и B установлены на верхних уровнях (+1). В двух вторых они установлены на нижних уровнях (-1).


Предположим, нужно оценить влияние независимых вкладов факторов A и B на интересующую нас зависимую переменную. Ясно, что этот план неразумный, поскольку он не позволяет оценить главные эффекты ни для A, ни для B. Оценке поддается только один эффект – разница между Runs 1+2 - Опытами 1+2 и Runs 3+4 - Опытами 3+4, представляющими комбинацию эффектов A и B.

Чтобы оценить независимые вклады двух факторов, их уровни в четырех опытах должны быть установлены так, чтобы “столбцы” плана были независимыми друг от друга. Другими словами, столбцы матрицы плана (а их столько, сколько имеется параметров главных эффектов и взаимодействий, которые желательно оценить) должны быть ортогональными. Например, если план организован следующим образом:

Таблица 16
Таблица 16

  A B Run 1
Run 2
Run 3
Run 4

1 1 -1 -1	1 -1 1 -1

то столбцы, соответствующие A и B, ортогональны. Теперь вы можете оценить главный эффект A путем сравнения высокого уровня A для каждого уровня B с низким уровнем A для каждого уровня B; главный эффект B может быть оценен таким же образом.

Два столбца матрицы плана ортогональны, если сумма произведений их элементов равна нулю (иными словами, равно нулю их скалярное произведение). На практике часто возникают ситуации, когда, например, из-за потери некоторых данных или по другим причинам столбцы матрицы плана не полностью ортогональны. Общее правило здесь состоит в том, что чем более столбцы ортогональны, тем план лучше организован, тем больше информации относительно интересующих нас эффектов может быть извлечено. Поэтому одним из соображений при выборе стандартных центральных композиционных планов является нахождение планов, которые ортогональны или почти ортогональны.

Ротатабельные планы.
Ротатабельные планы.

Второе соображение состоит в том, что нужно делать, чтобы наилучшим образом извлечь максимальное количество (несмещенной) информации из плана. Не вдаваясь в подробности (смотрите монографии Box, Hunter и Hunter, 1978; Box и Draper, 1987, глава 14; смотрите также Deming и Morgan, 1993, глава 13), можно показать, что стандартная ошибка предсказания значений зависимой переменной пропорциональна



(1 + f(x)' * (X'X)?? * f(x))**?

где f(x) обозначает эффекты факторов соответствующей модели (f(x) - вектор, а f(x)' - транспонированный вектор f(x)), X - матрица плана; а X'X**-1 – матрица, обратная ковариационной матрице X'X. Deming и Morgan (1993) называют это выражение нормализованной неопределенностью, эту функцию также называют дисперсионной функцией (смотрите определение в Box и Draper (1987)). Количество неопределенности в предсказании значений зависимой переменной зависит от вариабельности точек плана и их ковариаций между опытами. (Заметим, что эта величина обратно пропорциональна определителю матрицы X'X; данный вопрос будет далее обсуждаться в разделе D- и A-оптимальных планов).

Очевидно, желательно выбрать план таким образом, чтобы извлечь наибольшую информацию о зависимой переменной и получить наименьшую неопределенность для прогноза ее будущих значений. Из приведенного выражения следует, что количество информации (или нормализованной информации согласно Deming и Morgan, 1993) обратно пропорционально нормализованной неопределенности.

Для простого ортогонального плана с 4-мя опытами, приведенного ранее, информационная функция равна

Ix = 4/(1 + x1? + x2?)

где x1 и x2 обозначают соответственно уровни факторов A и B, (смотрите Box и Draper, 1987).



Видно, что информационная функция постоянна на концентрических окружностях с центрами в начале координат. Таким образом, любое вращение исходных точек плана дает то же самое количество информации, то есть то же самое значение информационной функции. Поэтому говорят, что ортогональный план из 4-х опытов, приведенный выше, является ротатабельным (инвариантным относительно вращения).

Чтобы оценить нелинейные компоненты (квадратичные, второго порядка) соотношений между факторами и зависимой переменной, необходимо иметь, по крайней мере, 3 уровня соответствующих факторов. Как же выглядит информационная функция для простого факторного плана 3-на-3 в квадратичной модели (второго порядка), показанной в начале данного раздела?





Известно (см. Box и Draper, 1987 или Montgomery, 1991), что эта функция выглядит более сложно, содержит “карманы” с высокой плотностью в угловых областях (которые, вероятно, представляют малый интерес для экспериментатора) и, очевидно, не является постоянной на окружностях. Следовательно, она не ротатабельна. Это означает, что при различных вращениях точек плана будет извлекаться разное количество информации.

Звездные точки и ротатабельные планы второго порядка. Можно показать, что при добавлении так называемых звездных точек к простым (квадратным или кубическим) 2-уровневым факторным планам можно получить ротатабельные, а иногда и ортогональные или почти ортогональные планы. Например, к ротатабельному плану приводит добавление следующего ряда точек к простому ортогональному плану 2-на-2:

Таблица 17
Таблица 17

A B Run 1
Run 2
Run 3
Run 4
Run 5
Run 6
Run 7
Run 8
Run 9
Run 10

1  1 -1 -1 -1.414  1.414  0  0  0  0	1 -1  1 -1  0  0 -1.414  1.414  0  0

Первые четыре опыта в этом плане являются точками предыдущего факторного плана 2-на-2 (или квадратичными точками или кубическими точками); опыты с 5-го по 8-ой являются так называемыми звездными точками или осевыми точками, а опыты 9 и 10 – центральными точками.



Информационная функция этого плана для модели второго порядка (квадратичной модели) ротатабельна, т. е. постоянна на окружностях с центром в начале координат (иными словами, план стал ротатабельным). Альфа для ротатабельности и ортогональности
Альфа для ротатабельности и ортогональности

Две характеристики плана – ортогональность и ротатабельность – зависят от числа центральных точек плана и так называемого осевого расстояния a (альфа), которое равно расстоянию от звездных точек до центра плана (т. е. 1.414 для плана, показанного выше). Можно показать, (см. например, Box, Hunter, и Hunter, 1978; Box и Draper, 1987, Khuri и Cornell, 1987; Montgomery, 1991), что план ротатабелен, если:



= ( nc )?

где nc означает число кубических точек в плане (т. е. точек в факторной части плана).

Центральный композиционный план является ортогональным, если выбрать альфа так, чтобы:

= {[( nc + ns + n0 )? - nc?]? * nc/4}?

где
nc число кубических точек плана
ns число звездных точек плана
n0 число центральных точек плана

Чтобы сделать план одновременно (приближенно) и ортогональным, и ротатабельным, следует вначале выбрать осевое расстояние для ротатабельности, а затем добавить центральные точки (см. Khuri и Cornell, 1987) так, чтобы:

n0 4*nc? + 4 - 2k

где k означает число факторов плана.

Наконец, если имеется разбиение на блоки, Box и Draper (1987) дают следующую формулу осевого (аксиального) расстояния для достижения ортогональности, и (в большинстве случаев) также для получения приемлемых контуров информационной функции, т. е. контуров, близких к сферическим:

= [k*(l+ns0/ns)/(1+nc0/nc)]?

где
ns0  число центральных точек в звездной части плана
ns   число нецентральных звездных точек плана
nc0  число центральных точек в кубической части плана
nc   число нецентральных точек кубических точек плана
Доступные стандартные планы
Доступные стандартные планы

Стандартные центральные композиционные планы обычно строятся следующим образом: в качестве кубической части плана берется план 2**(k-p) и затем он дополняется звездными и центральными точками. Box и Draper (1987) перечислили ряд таких планов.

Малые композиционные планы.
Малые композиционные планы.

В стандартных планах кубическая часть обычно является планом разрешения V (или выше). Это, однако, не является обязательным, и в случаях, когда опыты дороги, или когда необходимо построить статистически наиболее мощный тест для проверки адекватности модели, можно выбрать кубическую часть планов с разрешением III. Например, это можно сделать с помощью планов Плакетта-Бермана. Hartley (1959) описал такие планы. Анализ центральных композиционных планов
Анализ центральных композиционных планов



Анализ центральных композиционных планов во многом подобен анализу 3**(k-p) планов. Программа подгоняет данные с помощью общей модели, описанной ранее; например, для двух переменных программа будет подгонять модель:

y = b0 + b1*x1 + b2*x2 + b12*x1*x2 + b11*x12 + b22*x22

Подогнанная поверхность отклика
Подогнанная поверхность отклика

Форму подогнанной поверхности отклика лучше всего представить в графическом виде, и вы можете строить как контурные диаграммы, так и диаграммы поверхности отклика (смотрите пример ниже).

Категоризованные поверхности отклика
Категоризованные поверхности отклика

Вы можете подогнать 3-х мерную поверхность к вашим данным, категоризованную по некоторым другим переменным. Например, если стандартный центральный композиционный план повторен 4 раза, очень полезно посмотреть, насколько подобны поверхности, получающиеся при подгонке в каждой реплике.



Графическое представление позволит вам убедиться в надежности результатов, а также выявить области, в которых имеются отклонения.



Очевидно, третья реплика дает поверхность, отличную от других. В репликах 1, 2 и 4 подогнанные поверхности очень похожи друг на друга. Таким образом, необходимо выяснить, что является причиной этого заметного отличия в третьей реплике плана.

В начало

Планы на латинских квадратах

Обзор
Обзор

Планы латинских квадратов используются в тех случаях, когда интересующие нас факторы имеют более двух уровней, и вы заранее знаете, что между факторами нет взаимодействий (или этими взаимодействиями можно пренебречь). Например, если вы хотите проверить воздействие 4 топливных присадок на снижение концентрации окиси азота и имеете в своем распоряжении 4 автомобиля и 4 водителя, то в принципе, можно поставить полный факторный эксперимент 4 x 4 x 4, который требует 64 опыта. Однако вас реально не интересуют (малые) взаимодействия между топливными присадками и водителями, топливными присадками и автомобилями, а также автомобилями и водителями. Больше всего вас интересует оценка главных эффектов, в особенности фактор топливных присадок.


В то же время хотелось бы иметь уверенность, что главные эффекты водителей и автомобилей не влияют на оценку главного эффекта топливных присадок (не смещают их). Если вы обозначите присадки буквами A, B, C и D, то план латинских квадратов, который позволит получить оценки несмешанных главных эффектов, выглядит следующим образом (смотрите также Box, Hunter и Hunter, 1978, стр. 263):

Таблица 18
Таблица 18

Car Driver 1 2 3 4 1
2
3
4

A D B C	B C D A	D A C B	C B A D

Планы на латинских квадратах
Планы на латинских квадратах

Пример, показанный выше, на самом деле является лишь одним из трех возможных расположений уровней факторов, позволяющих получить несмещенные оценки главных эффектов. Такое расположение факторов называется Латинским квадратом. Выше показан латинский квадрат 4 x 4. Вместо требующихся в полном факторном эксперименте 64 опытов достаточно выполнить только 16. Греко-латинские квадраты.
Греко-латинские квадраты.

Замечательное свойство латинских квадратов состоит в том, что они могут накладываться друг на друга, образуя Греко-латинские квадраты. Например, следующие два латинских квадрата 3 x 3 могут быть преобразованы в греко-латинский квадрат:



С помощью этого греко-латинского квадрата вы можете оценить главные эффекты четырех 3-х уровневых факторов (фактора строк, фактора столбцов, римских букв и греческих букв) проведя только 9 опытов.

Гипер-греко-латинские квадраты.
Гипер-греко-латинские квадраты.

Для некоторого числа уровней имеется более двух возможных расположений в латинские квадраты. Например, существует три различных латинских квадрата на 4-х уровнях. Если их наложить друг на друга, получится план Гипер-греко-латинских квадратов. С его помощью можно оценить главные эффекты всех пяти 4-уровневых факторов, проведя эксперимент только с 16 опытами. Анализ плана
Анализ плана

Анализ планов латинских квадратов прост. Кроме того, могут быть получены диаграммы средних для интерпретации результатов.


Очень большие планы, случайные эффекты, несбалансированные вложения


Очень большие планы, случайные эффекты, несбалансированные вложения

Заметим, что имеется несколько методов, которые также позволяют проводить анализ такого типа планов; обращайтесь к разделу Методы дисперсионного анализа для подробностей. В частности, в разделе Компоненты дисперсии и смешанная модель ANOVA/ANCOVA описаны весьма эффективные методы для анализа планов с несбалансированными вложениями (когда вложенные факторы имеют другие уровни внутри уровней факторов, в которые они вложены), очень больших вложенных планов (например, с более чем 200 уровнями в совокупности) или иерархически вложенных планов (включая или исключая случайные эффекты).

В начало

Методы Тагучи: робастное планирование эксперимента

Обзор
Обзор

Приложения.
Приложения.

Методы Тагучи находят все большее применение в последние годы. Примеры значительного улучшения качества, связанного с внедрением этих методов (смотрите, например, Phadke, 1989; Noori, 1989), вызвали интерес к ним американских промышленников. Так, некоторые из ведущих производителей начали использовать их с очень большим успехом. Например, AT&T использует эти методы в производстве очень больших интегральных контуров (ОБИК), компания Форд добилась значительного улучшения качества, используя эти методы (Американский институт снабжения, 1984 по 1988). Обзор.
Обзор.

Методы Тагучи находятся во многих отношениях в стороне от традиционных процедур контроля качества (смотрите Контроль качества и Анализ производственных процессов) и промышленного эксперимента. Особенно важными являются следующие понятия: функция потери качества, отношение сигнал/шум (С/Ш), ортогональные массивы Эти основные аспекты методов робастного планирования будут обсуждаться в следующих разделах. По этим методам недавно было опубликовано несколько монографий, например, Peace (1993), Phadke (1989), Ross (1988) и Roy (1990), и рекомендуется обращаться к ним для более детального изучения темы. Вводные обзоры идей Тагучи о качестве и его улучшении можно найти в работах Barker (1986), Garvin (1987), Kackar (1986) и Noori (1989). Функции качества и потерь качества


Функции качества и потерь качества

Что такое качество.
Что такое качество.

Тагучи начинает с вопроса, что такое качество? Нелегко дать простое определение качества; однако, если ваш новый автомобиль теряет скорость в центре напряженного перекрестка, подвергая вас и других участников движения риску, то вы говорите, что ваш автомобиль не обладает высоким качеством. Понятие противоположное качеству более простое: это общие потери для вас и для общества, обусловленные функциональной изменчивостью (изменчивостью) и неблагоприятными побочными эффектами, связанными с соответствующим продуктом. Таким образом, в качестве рабочего определения вы можете измерять качество в терминах этих потерь, и чем больше потери качества, тем ниже оно само.

Разрывная функция потерь.
Разрывная функция потерь.

Вы можете сформулировать гипотезу об общем классе и форме функции потерь. Предположим, что имеется особая идеальная точка высшего качества; например, превосходный автомобиль без каких-либо проблем с качеством. Обычно в статистическом контроле процессов (СКП, см. также Анализ производственных процессов) принято определять уровень допуска вокруг номинальной идеальной точки производственного процесса. Согласно традиционной точке зрения, используемой в методах СКП, если вы находитесь внутри допуска, у вас не возникает проблем с качеством. Другими словами, внутри зоны допуска потери качества равны нулю. Если вы вышли за его пределы, потери качества объявляются неприемлемыми. Так, согласно традиционной точке зрения, функция потерь качества является разрывной порогообразной функцией: если вы находитесь внутри зоны допуска, потери качества пренебрежимы, а когда вы выходите за его пределы, потери становятся неприемлемыми.

Квадратичная функция потерь.
Квадратичная функция потерь.

Зададимся вопросом: является ли кусочно-постоянная функция хорошей моделью для потери качества? Вернемся к примеру “превосходного автомобиля”. Имеется ли разница между автомобилем, с которым ничего не случилось в течение года после покупки, и автомобилем, у которого начало что-то немножко барахлить, например, отвалились некоторые крепления и разбились часы на панели (все это входит в гарантийный ремонт, не так ли...)? Если вы когда-либо покупали новый автомобиль, вы очень хорошо знаете, как могут раздражать такие небольшие по общему признанию проблемы с качеством.


Точка зрения здесь такова: не является реалистичным предположение о том, что если вы удаляетесь от номинального определения вашего производственного процесса, потери качества равны нулю, если вы находитесь в зоне допуска. Наоборот, если вы не попали точно “в цель”, то потери все же существуют, например, в терминах удовлетворения покупателя. Более того, эти потери, вероятно, не являются линейной функцией отклонения от номинальной спецификации процесса, а являются квадратичной функцией арочного типа (вроде перевернутой буквы U). Шум в одном месте вашего автомобиля раздражает, но вы, вероятно, не будете слишком опечалены этим; но добавьте еще пару шумов и, возможно, вы объявите ваш автомобиль “хламом”. Если постепенные отклонения от номинала дают непропорциональное увеличение потерь, то скорее всего это квадратичные увеличения.

Вывод: контроль изменчивости.
Вывод: контроль изменчивости.

Если фактически потери качества являются квадратичной функцией отклонения от номинального значения, то цель ваших усилий состоит в том, чтобы минимизировать квадрат отклонения или дисперсию продукта относительно его номинальной (идеальной) спецификации, а не число единиц внутри границы допуска (как это делается в традиционных процедурах анализа процессов). Отношения (С/Ш) сигнал/шум
Отношения (С/Ш) сигнал/шум

Измерение потери качества.
Измерение потери качества.

Даже если вы заключили, что функция потерь квадратична, вы до сих пор точно не знаете, как измерять сами потери. Однако, на какой бы мере вы ни остановились, она должна отражать квадратичную природу функции.

Сигнал, шум и управляющие факторы.
Сигнал, шум и управляющие факторы.

Продукт идеального качества всегда должен откликаться одинаковым образом на управляющие сигналы. Когда вы поворачиваете ключ зажигания автомобиля, то ожидаете, что стартер провернет двигатель, и он заведется. В автомобиле идеального качества процесс зажигания всегда происходит одним и тем же образом, например, после трех поворотов ключа зажигания двигатель заводится.


Если в ответ на один и тот же сигнал - поворот ключа зажигания - наблюдается случайная изменчивость процесса, вы имеете дело с качеством, худшим, чем идеальное. Например, из-за таких неконтролируемых факторов, как низкая температура, влажность, изношенность двигателя и так далее последний может иногда завестись только после 20 попыток и даже не завестись совсем. Этот пример иллюстрирует ключевой принцип измерения качества по Тагучи: вам хотелось бы минимизировать изменчивость реакции продукта в ответ на факторы шума, максимизируя при этом изменчивость в ответ на управляющие факторы.

Факторы Шума - это те факторы, которые находятся вне контроля оператора. В примере с автомобилем эти факторы включают колебания температуры, различия в качестве бензина, изношенность двигателя и так далее. Управляющие факторы – это те факторы, которые устанавливаются или управляются оператором машины для ее использования по назначению (поворот ключа зажигания запускает двигатель и автомобиль может начать движение).

Итак, целью ваших усилий по улучшению качества является установка наилучших значений управляющих факторов, которые включены в производственный процесс для того, чтобы максимизировать отношение С/Ш (сигнал-шум); так что здесь факторы в эксперименте выступают как управляющие.

С/Ш отношения.
С/Ш отношения.

Вывод из предыдущего состоит в том, что качество может быть рассмотрено с точки зрения отклика продукта на шумы и управляющие факторы. Идеальный продукт будет реагировать только на сигналы оператора, и не будет реагировать на случайный шум (погоду, температуру, влажность и так далее). Следовательно, цель ваших усилий по совершенствованию качества может рассматриваться как попытка максимизировать отношение сигнал/шум (С/Ш) соответствующего продукта. Отношения С/Ш, описанные в последующих параграфах, были предложены Тагучи (1987).

Меньше - лучше.
Меньше - лучше.

Если вы хотите минимизировать число появлений некоторых дефектов продукта, вычислите следующее отношение С/Ш:

Eta = -10 * log10 [(1/n) * (yi2)]for i = 1 to no.


vars     see outer arrays

Здесь Eta является результирующим отношением С/Ш, n - число наблюдений, а y - соответствующая характеристика. Например, число повреждений окраски автомобиля могло бы выступать как переменная y и анализироваться посредством отношения С/Ш. Эффект управляющих факторов равен нуло, поскольку нуль повреждений окраски является желаемым состоянием. Заметим, что отношение С/Ш является выражением предполагаемой квадратичной функции потерь. Множитель -10 указывает на то, что это отношение измеряет величину, противоположную “плохому качеству”: чем больше повреждений окраски, тем больше сумма квадратов чисел повреждений и тем меньше (то есть более отрицательным) становится отношение С/Ш. Максимизация этого отношения приводит к возрастанию качества.

Номинальное – наилучшее значение.
Номинальное – наилучшее значение.

Здесь вы имеете фиксированную величину сигнала (номинальное значение), и дисперсия вокруг этого значения рассматривается как результат действия шумов:

Eta = 10 * log10 (Mean2/Variance)

Такое отношение сигнал/шум может использоваться, когда идеальное качество совпадает с конкретным номинальным значением. Например, диаметр поршневых колец в двигателе автомобиля должен быть как можно ближе к стандартному, чтобы обеспечить высокое качество двигателя.

Больше - лучше.
Больше - лучше.

Примерами такого типа инженерных задач является экономия топлива автомобиля (литров бензина на километр), прочность цементного раствора, сопротивление защитных материалов и так далее. Здесь используется следующее отношение С/Ш:

Eta = -10 * log10 [(1/n) * (1/yi2)]for i = 1 to no. vars     see outer arrays

Цель со знаком. Этот тип отношения С/Ш применяется, когда характеристика качества имеет идеальное значение 0 (ноль) и могут встречаться как положительные, так и отрицательные значения качества (отклонения от 0). Например, причиняющее ущерб напряжение в дифференциальных усилителях постоянного тока может быть как положительным, так и отрицательным (смотрите Phadke, 1989).


Можно воспользоваться следующим отношением С/Ш для проблем такого типа:

Eta = -10 * log10(s2)     for i = 1 to no. vars     see outer arrays

где s2 обозначает дисперсию характеристики качества по измерениям (переменным).

Доля дефектов.
Доля дефектов.

Это отношение С/Ш используется для минимизации отходов, минимизации доли пациентов, у которых развиваются побочные реакции на препарат, и так далее. Тагучи также ссылается на значения Эта как на значения Омеги. Заметим, что это отношение С/Ш эквивалентно известному преобразованию логит (смотрите главу Нелинейное оценивание):

Eta = -10 * log10[p/(1-p)]

где
p доля дефектных изделий

Упорядоченные категории (аккумуляционный анализ).
Упорядоченные категории (аккумуляционный анализ).

В некоторых случаях измерения характеристики качества могут быть получены только в терминах категорий. Например, покупатели могут категоризировать товар как превосходный, хороший, средний или ниже среднего. В этом случае вы пытаетесь максимизировать количество продуктов, оцениваемых как превосходные и хорошие. Обычно результат аккумуляционного анализа представляется в виде гистограммы. Ортогональные массивы
Ортогональные массивы

Третий аспект робастных планов Тагучи весьма схож с трациционными методами. Тагучи разработал систему табулированных планов, которые позволяют оценить несмещенным (ортогональным) образом максимальное число главных эффектов при помощи минимального числа опытов в эксперименте. Планы на латинских квадратах, 2**(k-p) планы (Планы Плакетта-Бермана, в частности), и Планы Бокса-Бенкена также предназначены для достижения этой цели. Многие стандартные ортогональные массивы, табулированные Тагучи, идентичны дробным факторным двухуровневым планам, планам Плакетта-Бермана, планам Бокса-Бенкена, латинским квадратам, греко-латинским квадратам и так далее.


Анализ планов
Анализ планов

Большая часть робастных планов эквивалентна обычному дисперсионному анализу (ДА) для соответствующих отношений С/Ш, в котором игнорируются взаимодействия второго порядка и выше.


Заметим, что при оценке дисперсий ошибок обычно объединяются вместе главные эффекты пренебрежимых размеров.

Анализ отношений С/Ш в стандартных планах.
Анализ отношений С/Ш в стандартных планах.

Следует заметить, что все обсуждавшиеся ранее планы (например, 2**(k-p) планы, 3**(k-p) планы, смешанные 2-х и 3-х уровневые планы, латинские квадраты, центральные композиционные планы) могут быть использованы для анализа отношений С/Ш, которые вы вычислили. На самом деле, многие дополнительные диаграммы или другие опции, имеющиеся для указанных планов (например, оценивание квадратичных компонент и так далее), могут оказаться очень полезными при анализе вариабельности (С/Ш отношений) в производственном процессе.

Диаграмма средних.
Диаграмма средних.

Визуализация итогов эксперимента состоит в нанесении на график средних Эта (С/Ш отношений) по уровням факторов. По этой диаграмме легко могут быть установлены оптимальные значения (то есть наибольшие отношения С/Ш) каждого фактора.

Проверочные или тестовые эксперименты.
Проверочные или тестовые эксперименты.

Для целей предсказания вы можете вычислить ожидаемое отношение С/Ш, при фиксировании пользователем определенных комбинаций установок факторов (игнорируя факторы, отнесенные в член ошибок). Эти предсказанные отношения С/Ш могут быть затем использованы для проведения проверочного эксперимента, в котором инженер действительно настраивает машину соответственно и сравнивает результаты наблюдаемого отношения С/Ш с предсказанным из предыдущего эксперимента отношением С/Ш. Если случаются большие отклонения, нужно сделать вывод, что модель простых главных эффектов не подходит.

В таких случаях Тагучи рекомендует преобразование зависимой переменной для обеспечения аддитивности факторов, то есть попытаться “заставить” модель главных эффектов соответствовать (Taguchi, 1987). Phadke (1989, глава 6) также детально обсуждает методы обеспечения аддитивности факторов. Аккумуляционный анализ
Аккумуляционный анализ

Для анализа упорядоченных категориальных данных дисперсионный анализ непригоден.


Вместо него модуль Планирование эксперимента представит кумулятивный график числа наблюдений в каждой категории. Для каждого уровня фактора программа выведет накопленную (кумулятивную) долю числа дефектных изделий. Таким образом, эта диаграмма дает ценную информацию относительно распределения категориальных отсчетов при различных значениях факторов. Выводы
Выводы

Вначале вы должны определить факторы плана или управляющие факторы, которые могут быть установлены конструктором или инженером. Это факторы эксперимента, которые вы будете устанавливать на различные уровни. Затем вы примете решение об использовании соответствующего ортогонального массива для эксперимента. Далее вы должны решить, как измерять интересующую вас характеристику качества. Помните, что большинство отношений С/Ш требует, чтобы в каждом опыте эксперимента производились многократные измерения, в противном случае, например, изменчивость (разброс) вокруг номинального значения не может быть оценена. Наконец, вы проводите эксперимент и определяете факторы, наиболее сильно влияющие на выбранное отношение С/Ш, и соответственно регулируете вашу машину или производственный процесс.

В начало

Планы для смесей и тернарные поверхности

Обзор
Обзор

Специальные вопросы возникают, когда анализируются смеси компонент, которые в сумме должны давать константу. Например, если вы хотите оптимизировать вкус фруктового пунша, состоящего из соков 5 фруктов, то сумма долей всех соков в каждой смеси должна быть равна 100%. Такая задача оптимизации смесей часто встречается в производстве пищи, очистке или производстве химикатов или лекарств. Разработан ряд планов, специально для анализа смесей (смотрите, например, Cornell, 1990a, 1990b; Cornell и Khuri, 1987; Deming и Morgan, 1993; Montgomery, 1991).


Треугольные координаты
Треугольные координаты

Общим способом, с помощью которого могут быть представлены пропорции в смеси, являются треугольные диаграммы (диаграммы на треугольнике). Например, предположим, что у вас есть смесь, которая состоит из 3 компонент A, B, C.


Любая смесь трех компонент может быть представлена точкой в системе координат на треугольнике, определяемой тремя переменными.

Например, возьмем следующие 6 смесей из 3-х компонент.

Таблица 19
Таблица 19

A B C

1 0 0 0.5 0.5 0	0 1 0 0.5 0 0.5	0 0 1 0 0.5 0.5

Сумма для каждой смеси равна 1.0, так что значения компонент в каждой смеси могут интерпретироваться как пропорции. Если вы нанесете эти данные на график в виде обычной 3-х мерной диаграммы рассеяния, станет очевидно, что точки образуют треугольник в 3-х мерном пространстве. Только точки внутри треугольника, где сумма значений компонент равна 1, представляют настоящие смеси. Следовательно, можно просто наносить данные только в треугольник (в данном случае двумерный), чтобы изображать значения компонент (пропорции) для каждой смеси.



Чтобы определить координаты точки в треугольном графике, вы соединяете прямой линией точку с вершинами треугольника.



Вершина, соответствующая конкретному фактору представляет собой чистую смесь, то есть состоящую только из данной компоненты. Так что координата соответствующей вершине компоненты равна 1 (или 100% или любой другой величине в зависимости от шкалирования) и равна 0 (нулю) для всех других компонент. На стороне, противоположной соответствующей вершине, значение данной компоненты равно 0 (нулю), а для других компонент .5 (или 50% и так далее). Тернарные поверхности и контуры
Тернарные поверхности и контуры

Можно теперь добавить четвертое измерение и нанести на график значения зависимой переменной или функцию (поверхность) для каждой точки внутри треугольника. Заметим, что поверхность отклика может быть представлена либо в 3-х мерном пространстве, где предсказываемый отклик (оценка Taste -Вкуса) наносится, как расстояние поверхности от плоскости треугольника, либо представлена в виде контурной диаграммы, где контуры равной высоты наносятся в 2-х мерном треугольнике.



Здесь следует упомянуть о том, что категоризованные графики позволяют построить категоризованные диаграммы, заданные на треугольнике.


Они полезны, поскольку позволяют вам подгонять зависимую переменную (например, Taste -Вкус) поверхностью отклика для различных уровней четвертой компоненты. Канонический вид полиномов для смесей
Канонический вид полиномов для смесей

Подгонка поверхности отклика к данным по смесям, в принципе, осуществляется таким же образом, как и подгонка поверхности для данных, полученных, например, с помощью центральных композиционных планов. Однако имеется проблема, состоящая в том, что в данных о смесях накладывается ограничение, состоящее в том, что сумма значений компонент должна быть постоянной.

Рассмотрим простой пример с двумя факторами A и B. Желательно подогнать простую линейную модель:

y = b0 + bA*xA + bB*xB

Здесь y обозначает зависимую переменную, bA и bB обозначают коэффициенты регрессии, xA и xB - значения факторов. Предположим, что xA и xB должны в сумме давать 1; тогда вы можете умножить b0 на 1=(xA + xB):

y = (b0*xA + b0*xB) + bA*xA + bB*xB

или:

y = b'A*xA + b'B*xB

где b'A = b0 + bA и b'B = b0 + bB. Таким образом, оценивание в этой модели сводится к подгонке модели множественной регрессии без свободного члена. (Смотрите также Множественная регрессия для более детального рассмотрения вопросов, касающихся регрессии). Общие модели для смесей
Общие модели для смесей

Квадратичную и кубическую модели также можно упростить (как показано выше на примере простой линейной модели), что приводит к четырем стандартным моделям, обычно применяемым для подгонки смесей. Здесь приведены формулы для 3-х переменных для таких моделей (смотрите Cornell, 1990, для дополнительных подробностей).

Линейная модель:

y = b1*x1 + b2*x2 + b3*x3

Квадратичная модель:

y = b1*x1 + b2*x2 + b3*x3 + b12*x1*x2 + b13*x1*x3 + b23*x2*x3

Специальная кубическая модель:

y = b1*x1 + b2*x2 + b3*x3 + b12*x1*x2 + b13*x1*x3 + b23*x2*x3 + b123*x1*x2*x3

Полная кубическая модель:

y = b1*x1 + b2*x2 + b3*x3 + b12*x1*x2 + b13*x1*x3 + b23*x2*x3 + d12*x1*x2*(x1 - x2) + d13*x1*x3*(x1 - x3) + d23*x2*x3*(x2 - x3) + b123*x1*x2*x3



(Заметим, что коэффициенты dij также являются параметрами модели). Стандартные планы экспериментов для смесей
Стандартные планы экспериментов для смесей

Обычно используются два типа стандартных планов экспериментов для смесей. Оба они оценивают поверхности отклика в вершинах треугольника и в центрах сторон. Иногда в эти планы добавляют дополнительные внутренние точки.

Симплекс-вершинные планы.
Симплекс-вершинные планы.

При этом размещении точек плана m+1 для каждого фактора или компоненты в модели тестируются равноразмещенные точки:

xi = 0, 1/m, 2/m, ..., 1i = 1,2,...,q

а также все их комбинации. Получающийся план называется simplex-lattice – симплекс-вершинным планом. Например, симплекс-вершинный план с {q=3, m=2} включает следующие смеси:

Таблица 20
Таблица 20

A B C

1 0 0 .5 .5 0	0 1 0 .5 0 .5	0 0 1 0 .5 .5

Симплекс-вершинный план с {q=3,m=3} включает следующие точки:

Таблица 21
Таблица 21

A B C

1 0 0 1/3 1/3 0 2/3 2/3 0 1/3	0 1 0 2/3 0 1/3 1/3 0 2/3 1/3	0 0 1 0 2/3 2/3 0 1/3 1/3 1/3

Симплекс-центроидные планы. Альтернативное размещение факторов, введенное Шеффе (Scheffe, 1963), является так называемым симплекс-центроидным планом. При его применении точки плана соответствуют всем перестановкам чистых смесей (например, 1 0 0; 0 1 0; 0 0 1), перестановкам бинарных смесей (Ѕ Ѕ 0; Ѕ 0 Ѕ; 0 Ѕ Ѕ), перестановкам с тремя одинаковыми по пропорции компонентами и так далее. Например, для 3-х факторов симплекс-центроидный план состоит из точек (вершины, центры сторон, центр треугольника):

Таблица 22
Таблица 22

A B C

1 0 0 1/2 1/2 0 1/3	0 1 0 1/2 0 1/2 1/3	0 0 1 0 1/2 1/2 1/3

Добавление внутренних точек. Подобные планы иногда дополняются внутренними точками (смотрите Khuri и Cornell, 1987, стр. 343; Mason, Gunst, Hess; 1989; стр. 230). Например, для 3-х факторов можно добавить следующие внутренние точки:

Таблица 23
Таблица 23

A B C

2/3 1/6 1/6	1/6 2/3 1/6	1/6 1/6 2/3

Если вы нанесете их на диаграмму рассеяния в треугольных координатах, можно увидеть, как ровно эти планы заполняют экспериментальную область, определенную на треугольнике.


Ограничения снизу
Ограничения снизу

Для всех планов, описанных выше, требуются точки-вершины, то есть чистые смеси, состоящие из одной компоненты. На практике такие точки обычно неприемлемы, т.к. не могут производиться из-за соображений стоимости или других ограничений. Например, предположим, что вы хотели бы изучить эффект пищевых добавок на вкус фруктового пунша. Дополнительный ингредиент может варьироваться лишь в узких пределах, например, он не может превышать некоторого процента общей массы. Ясно, что фруктовый пунш, составленный только из чистой добавки, не будет на самом деле пуншем. Такого рода ограничения весьма типичны.

Рассмотрим пример с тремя компонентами, где на компоненту A наложено ограничение xA.3. Общая сумма для 3-х компонентной смеси должна быть равной 1. Это ограничение может быть показано на треугольной диаграмме в виде прямой с треугольными координатами для xA=.3, то есть прямой, параллельной стороне треугольника, противоположной вершине A.



Теперь можно построить план, как и ранее, с тем лишь условием, что одна компонента смеси удовлетворяет ограничению. Позднее, при проведении анализа, можно просмотреть оценки параметров так называемых псевдокомпонент, рассматривающих ограниченный треугольник как полный.

Множественные ограничения.
Множественные ограничения.

Многомерные ограничения снизу можно рассматривать аналогично одномерным. Программа сконструирует множество внутри полного треугольника и затем поместит точки плана в нее согласно выбранному плану. Ограничения сверху и снизу
Ограничения сверху и снизу

Если имеются ограничения снизу и сверху (что часто бывает в экспериментах на смесях), то стандартные симплекс-вершинные и симплекс-центроидные планы не могут быть построены, поскольку область, определяемая ограничениями, не является больше треугольником и центры (например, вершины) могут не принадлежать области определения.


Существует общий алгоритм нахождения точек-вершин и центроидов для таких планов с ограничениями.



Заметим, что вы все еще можете проводить анализ таких планов, подгоняя стандартные модели. Анализ экспериментов для смесей
Анализ экспериментов для смесей

Анализ экспериментов для смесей похож на множественную регрессию со свободным членом, равным нулю. Как объяснялось ранее, основное ограничение: сумма всех компонент должна быть постоянной – может быть реализовано в подгонке модели множественной регрессии, не включающей свободный член. Если вы не знакомы с понятием множественной регрессии, смотрите Множественная регрессия.

Специальные модели, рассматриваемые обычно, описаны ранее. Суммируя это описание, отметим, что к значениям зависимой переменной подгоняется поверхность отклика возрастающей сложности, начиная с линейной модели, затем продолжая квадратичной моделью, специальной кубической моделью и, наконец, завершая полной кубической моделью. Ниже приведена таблица, показывающая число членов или параметров в каждой модели для некоторого числа компонент (смотрите таблицу 4, Cornell, 1990):

Таблица 24
Таблица 24

Model (Degree of Polynomial) No. of
Comp.  
Linear  
Quadr. Special
Cubic Full
Cubic 2
3
4
5
6
7
8

2 3 4 5 6 7 8	3   6 10 15 21 28 36	--   7 14 25 41 63 92	--   10   20   35   56   84 120

Дисперсионный анализ
Дисперсионный анализ

Для того чтобы решить, какая модель из иерархии моделей возрастающей сложности дает достаточно хорошее согласие с наблюдаемыми данными, обычно их сравнивают пошагово. Например, рассмотрим смесь 3-х компонент, к которой подгоняется полная кубическая модель.

ANOVA; Var.:DV (mixt4.sta)   3 Factor mixture design; Mixture total=1., 14 Runs
Sequential fit of models of increasing complexity  
Model SS
Effect df
Effect MS
Effect SS
Error df
Error MS
Error  
F  
p  
R-sqr R-sqr
Adj. Linear
Quadratic
Special Cubic
Cubic
Total Adjusted

44.755 30.558 .719 8.229 91.627	2 3 1 3 13	22.378 10.186 .719 2.743 7.048	46.872 16.314 15.596 7.367	11 8 7 4	4.2611 2.0393 2.2279 1.8417	5.2516 4.9949 .3225 1.4893	.0251 .0307 .5878 .3452	.4884 .8220 .8298 .9196	.3954 .7107 .6839 .7387

Вначале подгоняется линейная модель. Хотя эта модель имеет 3 параметра: по одному для каждой компоненты, имеется только 2 степени свободы. Это происходит из-за общего ограничения (сумма всех значений компонент смеси постоянна). Одновременный тест для всех параметров этой модели статистически значим (F(2,11)=5.25; p<.05). Добавление 3-х параметров квадратичной модели (b12*x1*x2, b13*x1*x3, b23*x2*x3) увеличивает согласие (F(3,8)=4.99; p<.05). Однако добавление параметров специальной кубической и полной кубической модели не приводит к статистически значимому увеличению согласия подгоняемой поверхности. Таким образом, можно сделать вывод, что квадратичная модель обеспечивает адекватное согласие с данными (конечно, мы пока откладываем изучение остатков для выскакивающих наблюдений и тому подобные вопросы).

R-квадрат (коэффициент детерминации). Таблица ДА содержит также R-квадрат (коэффициент детерминации) соответствующей модели. Значения R-квадрат могут интерпретироваться как доля изменчивости зависимой переменной относительно среднего. Заметим, что для моделей без свободного члена некоторые программы множественной регрессии вычисляют значения R-квадрат только для доли дисперсии вокруг 0 (нуля), обусловленной независимыми переменными; (для получения большей информации смотрите Kvalseth, 1985; Okunade, Chang, и Evans, 1993).

Чистая ошибка и потеря согласия.
Чистая ошибка и потеря согласия.

Полезность оценивания чистой ошибки для установления общей потери согласия было ранее обсуждено в разделе о центральных композиционных планах. Если некоторые опыты плана повторяются (реплицируются), то можно вычислить оценку дисперсии ошибки. Эта оценка дает хорошее представление о ненадежности измерений независимо от подгоняемой модели, поскольку основывается на одинаковых установках факторов (смесей в нашем случае). Можно тестировать остаточную изменчивость после подгонки текущей модели, используя эту оценку чистой ошибки. Если этот тест статистически значим, то есть остаточная изменчивость значительно больше вариабельности, обусловленной чистой ошибкой, тогда можно сделать вывод, что, вероятно, имеются дополнительные существенные различия между смесями, не описываемые текущей моделью.


Таким образом, может иметь место общая потеря согласия текущей модели. В этом случае попытайтесь использовать более сложную модель, вероятно добавляя в нее отдельные члены из модели более высокого порядка (например, добавляя только член b13*x1*x3 в линейную модель). Оценки параметров
Оценки параметров

Обычно после подгонки конкретной модели следует просмотреть оценки параметров. Заметим, что на линейные члены в моделях для смесей наложены ограничения (сумма компонент должны быть константой). Следовательно, независимые критерии значимости не могут быть выполнены. Псевдокомпоненты
Псевдокомпоненты

Чтобы избежать влияния разных шкал измерения компонет смеси обычно их перекодируют в так называемые псевдокомпоненты (смотрите также Cornell, 1993, глава 3):

x'i = (xi-Li)/(Total-L)

Здесь x'i обозначает i-ую псевдокомпоненту, xi обозначает исходные значения компоненты, Li – ограничение снизу (предел) для i-ой компоненты, L – сумма всех ограничений снизу для всех компонент плана, а Total есть суммы значений всех компонент смеси.

Вопрос об ограничениях снизу также обсуждался в этом разделе. Если план является стандартным симплекс-вершинным или симплекс-центроидным, то это преобразование приводит просто к другой шкале измерения факторов (строится субтреугольник (субсимплекс), определяемый ограничениями снизу). Однако вы можете вычислять оценки параметров, основываясь на исходной (не преобразованной) метрике компонент, участвующих в эксперименте. Если вы используете подогнанные значения параметра для целей прогноза (то есть предсказываете значения зависимой переменной), то часто более удобно использовать параметры для непреобразованных компонент. Заметим, что диалоговый режим получения результатов в экспериментах для смесей содержит опции для прогноза зависимой переменной в задаваемых пользователем значениях компонент в исходной метрике. Графические опции
Графические опции

Поверхности и контуры.
Поверхности и контуры.

Конкретная подогнанная модель может быть визуализирована в виде диаграммы поверхности на треугольнике или в виде контурной диаграммы, которая, по желанию, может также включать соответствующую подогнанную функцию.





Заметим, что подогнанная функция, представленная в виде поверхности или контурной диаграммы, всегда соответствует оценкам параметров для псевдокомпонент.

Категоризованные поверхности.
Категоризованные поверхности.

Если план содержит реплики, и они закодированы в вашем массиве данных, то вы можете использовать Категоризованные графики для просмотра соответствующих подгонок, реплика за репликой.



Конечно, если у вас есть другие категориальные переменные (например, оператор или экспериментатор, машина и так далее), вы можете также категоризовать 3-х мерную диаграмму поверхности и для таких переменных.

Графики следа отклика. Одним из методов оказания помощи при интерпретации поверхности отклика на треугольнике является график следа ожидаемого отклика. Предположим, что вы смотрите на контурную диаграмму поверхности отклика для трех компонент. Тогда определим базисную смесь двух компонент, например, установив A и B на уровне 1/3. Удерживая относительные пропорции A и B постоянными (то есть равными установленным значениям), вы можете нанести на диаграмму оценку отклика (значения зависимой переменной) для различных значений C.



Если базисная смесь для A и B составляет 1:1, то линия следа является осью фактора C; то есть прямой между вершиной C и серединой противоположной стороны треугольника. Графики следа для других смесей также могут быть получены. Обычно на графике видны следы всех компонент для конкретной базисной смеси.

Графики остатков.
Графики остатков.

Наконец, весьма важно после принятия решения о выборе модели, просмотреть остатки, чтобы найти выбросы и определить области плохой и хорошей подгонки. Кроме того, следует просмотреть стандартный нормальный график остатков и диаграмму рассеяния наблюдаемых значений против предсказываемых. Помните, что множественная регрессия (подгонка поверхности) предполагает, что остатки распределены нормально, и следует тщательно просмотреть остатки на наличие выбросов).

В начало

Планы для поверхностей и смесей с ограничениями



Обзор
Обзор

Как уже говорилось при обсуждении планов для смесей, на интересующие нас экспериментальные области могут быть наложены ограничения. Пипель и Сни (Piepel, 1988) и Snee, 1985) предложили алгоритм для нахождения вершин и центроидов в областях с ограничениями.


Планы для экспериментальных областей с ограничениями
Планы для экспериментальных областей с ограничениями

Когда в эксперименте со многими факторами имеются ограничения на значения факторов и их комбинаций, не ясно, как подойти к решению такой задачи. Разумный подход состоит в включении в эксперимент экстремальных вершинных точек и центроидов ограниченной области, которые обычно образуют хорошее ее покрытие (например, смотрите Piepel, 1988; Snee, 1975). В самом деле, планы для смесей, рассмотренные в предыдущем разделе, дают примеры таких планов, поскольку они обычно строятся так, чтобы включать в эксперимент вершины и центры ограниченной области, содержащейся в треугольнике (симплексе).


Линейные ограничения
Линейные ограничения

Обычный способ задания большинства ограничений состоит в применении линейных неравенств (смотрите Piepel, 1988):

A1x1 + A2x2 + ... + Aqxq + A0 0

Здесь A0, .., Aq являются параметрами линейного ограничения, наложенного на q факторов, а x1,.., xq обозначают значения факторов (уровни) для q факторов. Эта общая формула может описать даже очень сложные ограничения. Например, предположим, что в двухфакторном эксперименте первый фактор всегда должен быть установлен на уровнях по крайней мере в два раза больших второго фактора, что может быть записано в виде: x1 2*x2. Это простое ограничение далее может быть переписано как: x1-2*x2 0. Ограничение в виде отношения 2*x1 /x2 1 может быть записано в виде 2*x1 - x2 0 и так далее.

Проблема нескольких ограничений сверху и снизу на значения компонент смеси была обсуждена ранее в связи с экспериментами для смесей. Например, предположим, что в 3-х компонентной смеси фруктовых соков ограничения сверху и снизу на компоненты таковы (смотрите пример 3.2 в работе Cornell 1993):



40% Watermelon (x1) 80%
10% Pineapple (x2) 50%
10% Orange (x3) 30%

Эти ограничения могут быть переписаны как линейные ограничения в виде:

Watermelon:	x1-40 0 -x1+80 0
Pineapple:	x2-10 0 -x2+50 0
Orange:	x3-10 0 -x3+30 0

Таким образом, проблема нахождения точек плана для экспериментов на смесях с компонентами, на которые наложено несколько ограничений сверху и снизу, является частным случаем общих линейных ограничений. Алгоритм Пипеля и Сни
Алгоритм Пипеля и Сни

Для специального случая смесей с ограничениями часто используются алгоритмы типа XVERT (см., например, Cornell, 1990) для того чтобы найти вершинные и центроидные точки для ограниченных областей (внутри треугольника, тетраэдра). Пипелем и Сни (Piepel, 1988 и Snee, 1979) был предложен общий алгоритм для нахождения вершин и центров тяжести (центроидов) и приложимый как к смесям, так и к не-смесям. Общий подход подробно описан Сни (Snee, 1979).

А именно, программа рассматривает ограничения, записанные с помощью линейных неравенств, как это было описано выше, одно за другим. Каждое ограничение описывает прямую (или гиперплоскость), проходящую в экспериментальной области. Для каждого последовательного ограничения программа оценивает, пересекает ли она текущую ограниченную область. Если это так, вычисляются новые вершины, определяющие новую экспериментальную область, подправленную с учетом последнего ограничения. Затем проверяется, не становятся ли предыдущие ограничения излишними, то есть определяют прямую или плоскость, целиком находящуюся вне рассматриваемой области. После того как обработаны все ограничения, программа вычисляет центроиды для сторон ограниченной области (упорядоченные по запросу пользователя). В двумерном (двухфакторном) случае можно легко воссоздать этот процесс, просто проводя прямые через экспериментальную область (по одной на ограничение), так что получится искомая область.



Для более подробной информации, см. оригинальные работы Piepel (1988) или Snee (1979).




Выбор точек эксперимента
Выбор точек эксперимента

Как только вершины и центры вычислены, вы сталкиваетесь с проблемой выбора подмножества точек для эксперимента. Если каждый его опыт дорогостоящ, то не разумно использовать все вершины и центроиды. В частности, если имеется много факторов и ограничений, то число центроидов может расти очень быстро.

Если вы просеиваете большое число факторов и не интересуетесь нелинейными эффектами, то, выбирая только вершины, как правило, получаете хорошее покрытие экспериментальной области. Чтобы увеличить статистическую мощность (увеличить число степеней свободы для члена ошибок дисперсионного анализа), можно включить несколько опытов с факторами, установленными в центроиде всей ограниченной области.

Если вы рассматриваете несколько моделей, которые могут подходить к данным, можно использовать опции D- и A-оптимальных планов, описанных в следующем разделе. Эти опции помогут отобрать точки плана, извлекая максимум информации из ограниченной экспериментальной области для ваших моделей. Анализ планов для поверхностей и смесей с ограничениями
Анализ планов для поверхностей и смесей с ограничениями

Как уже отмечалось в разделах о центральных композиционных планах и планах для смесей, если точки в ограниченной области выбраны для окончательного эксперимента, и интересующие нас значения зависимых переменных получены, анализ проводится стандартным образом.

Например, Cornell (1990, стр. 68) описывает эксперимент с тремя пластификаторами и их воздействие на толщину винилового покрытия автомобильных сидений. Производственные ограничения на три компоненты пластификатора x1, x2 и x3 следующие:

.409 x1 .849
.000 x2 .252
.151 x3 .274

(Заметим, что эти значения уже стандартизованы, так что их сумма для каждой смеси должна быть равна 1). Построенные вершины и центроидные точки, построенные таковы:

x1 x2 x3

.8490 .7260 .4740 .5970 .6615 .7875 .6000 .5355 .7230	.0000 .0000 .2520 .2520 .1260 .0000 .1260 .2520 .1260	.1510 .2740 .2740 .1510 .2125 .2125 .2740 .2125 .1510

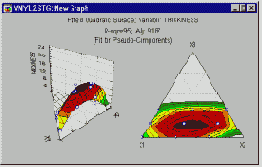
В начало

Построение D- и A-оптимальных планов

Обзор
Обзор

В разделе стандартных факторных планов (смотрите Дробные 2**(k-p) факторные планы и 3**(k-p) планы, планы Бокса-Бенкена, и Смешанные 2-х и 3-х уровневые планы) и центральных композиционных планов обсуждалось свойство ортогональности. Коротко говоря, если уровни установок факторов не коррелированы, то есть изменяются независимо друг от друга, то говорят, что они ортогональны. (Если вы знакомы с матричной и векторной алгеброй, два вектор-столбца X1 и X2 в матрице ортогональны, если X1'*X2= 0). Интуитивно понятно, что можно извлечь максимальное количество информации о зависимой переменной в экспериментальной области (область, определяемая мыслимыми уровнями установок факторов), если все эффекты факторов ортогональны друг другу. Обратно, предположим, что проводится эксперимент из четырех опытов для двух факторов следующим образом:

x1 x2 Run 1
Run 2
Run 3
Run 4

1  1 -1 -1	1  1 -1 -1

Здесь столбцы факторов X1 и X2 идентичны друг другу (их корреляция равна 1), и в результате невозможно различить главные эффекты факторов X1 и X2.

Процедуры D- и A-оптимальных планов предоставляют различные опции для отбора из списка подходящих точек-кандидатов (то есть комбинаций установок факторов) тех точек, которые извлекают из экспериментальной области максимальное количество информации для модели, которую вы хотите подогнать к данным. Вы уже имеете список точек-кандидатов, например, вершин и центроидов, вычисленных с помощью Планов для поверхностей и смесей с ограничениями, тип ожидаемой модели, число опытов. Тогда будет построен план с заданным числом опытов, который обеспечит максимальную ортогональность столбцов матрицы плана.

Смысл D- и A-оптимальности обсуждается, например, в монографии Бокса и Дрейпера (Box и Draper, 1987, глава 14). Различные алгоритмы, используемые для поиска оптимальных планов, обсуждаются в работах Dykstra (1971), Galil и Kiefer (1980) и Mitchell (1974a, 1974b).


Подробное сравнительное описание алгоритмов проводится в работе Cook и Nachtsheim (1980). Основные идеи
Основные идеи

Техническое обсуждение идей, лежащих в основе D- и A-оптимальных планов, а также их ограничения находятся за пределами этого обсуждения. Однако, основные идеи достаточно прозрачны. Рассмотрим снова простой двухфакторный эксперимент из четырех опытов:

  x1 x2 Run 1
Run 2
Run 3
Run 4

1  1 -1 -1	1  1 -1 -1

Как отмечалось выше, этот план, разумеется, не позволяет независимо проверить статистическую значимость вклада двух переменных для прогноза зависимой переменной. Если вы вычислите корреляционную матрицу двух переменных, то корреляция между ними будет равна 1:

  x1 x2 x1
x2

1.0 1.0	1.0 1.0

Обычно нужно планировать эксперимент таким образом, чтобы два фактора изменялись независимо друг от друга:

  x1 x2 Run 1
Run 2
Run 3
Run 4

1  1 -1 -1	1 -1  1 -1

Теперь две переменные некоррелированы, то есть их корреляционная матрица равна:

  x1 x2 x1
x2

1.0 0.0	0.0 1.0

Другой термин, обычно используемый в данном контексте - ортогональность. Если сумма произведений элементов двух столбцов (векторов) матрицы плана равна 0 (нулю), то два столбца ортогональны.

Определитель матрицы плана.
Определитель матрицы плана.

Определитель D квадратной матрицы (подобной корреляционной матрице 2 на 2, показанной выше) является числом, количественно выражающим независимость столбцов или строк матрицы или степень сводимости их друг к другу. Для случая 2 на 2 он просто равен произведению диагональных элементов минус произведение внедиагональных элементов (для матриц большей размерности вычисления более сложные). Например, для двух матриц, показанных выше, определитель D равен, соответственно:

D1 =	|1.0 1.0| |1.0 1.0|	= 1*1 - 1*1 = 0
D2 =	|1.0 0.0| |0.0 1.0|	= 1*1 - 0*0 = 1

Таким образом, определитель первой матрицы, получающийся из полностью вырожденной установки факторов, равен 0.


Определитель второй матрицы при ортогональных факторах равен 1.

D-оптимальные планы.
D-оптимальные планы.

Это базовое соотношение обобщается для матриц плана больших размерностей. Чем более зависимы векторы-столбцы матрица плана, тем более близок к 0 (нулю) детерминант корреляционной матрицы для этих векторов, а чем более независимы столбцы, тем больше детерминант этой матрицы. Таким образом, нахождение матрицы плана с максимальным детерминантом D означает нахождение плана, в котором эффекты факторов максимально независимы друг от друга. Этот критерий называется критерием D-оптимальности.

Матричные обозначения.
Матричные обозначения.

В действительности обычно проводятся вычисления с ковариационной (а не корреляционной) матрицей. В матричных обозначениях, если матрица плана обозначается X, то интересующая нас величина есть детерминант матрицы X’X (X-транспонированнная, умноженная на X). Таким образом, поиск D- optimal - D-оптимальных планов заключается в максимизации |X’X|, где (|..|) обозначают детерминант матрицы.

A-оптимальные планы.
A-оптимальные планы.

Другим способом взглянуть на проблему независимости является максимизация суммы диагональных элементов матрицы X’X при минимизации внедиагональных элементов. Так называемый критерий следа или критерий A-оптимальности воплощает эту идею. A-критерий определяется как:

A = trace(X'X)-1

где trace обозначает сумму диагональных элементов матрицы (X'X)-1.

Информационная функция.
Информационная функция.

Здесь следует упомянуть, что D-оптимальные планы минимизируют ожидаемую ошибку предсказания зависимой переменной, то есть такие плана будут максимизировать точность прогноза, а значит, информацию (которая определяется как обратная величина ошибки), извлекаемую из интересующей нас экспериментальной области. Измерение эффективности плана
Измерение эффективности плана

Было предложено несколько стандартных мер, суммарно оценивающих эффективность плана.

D-эффективность.
D-эффективность.

Эта мера связана с критерием D-оптимальности:



D-efficiency = 100 * (|X'X|1/p/N)

Здесь p обозначает число факторов-эффектов плана (столбцов в X), а N – число требуемых опытов. Эта мера может быть интерпретирована как относительное число опытов (в процентах), которое требовалось бы ортогональному плану для достижения той же величины детерминанта |X'X|. Однако ортогональный план часто нереален. Во многих случаях, это лишь теоретический критерий. Следовательно, вы должны использовать эту меру лишь как относительный индикатор эффективности для сравнения с другими планами того же объема, построенными из того же списка точек-кандидатов плана. Также заметим, что эта мера - единственно осмысленная (и только она может сообщаться), если вы решили, что факторы (то есть установки факторов точек из списка точек-кандидатов) имеют минимум -1 и максимум - +1.

A-эффективность.
A-эффективность.

Эта мера относится к критерию A-оптимальности:

A-efficiency = 100 * p/trace(N*(X'X)-1)

Здесь p обозначает число факторов-эффектов плана (столбцов в X), N – число требуемых опытов, а trace означает сумму диагональных элементов матрицы (N*(X'X)-1)) (след матрицы). Эта мера может интерпретироваться, как относительное число опытов (в процентах), которое потребовалось бы ортогональному плану для достижения той же самой величины следа (X'X)-1. Однако, снова отметим, что вы должны использовать эту меру как относительный индикатор эффективности для сравнения других планов того же объема, построенных из того же списка точек-кандидатов. Более того, это единственно осмысленная мера, если вы решили перекодировать установки факторов от -1 до +1.

G-эффективность.
G-эффективность.

Эта мера вычисляется как:

G-efficiency = 100 * square root(p/N)/M

Здесь как и ранее p обозначает число факторов-эффектов плана (столбцов в X), N – число требуемых опытов, а Again, p stands for the number of factor effects in the design and N is the number of requested runs; M (sigmaM) обозначает максимальную стандартную ошибку по множеству точек-кандидатов. Эта мера относится к так называемому критерию G-оптимальности; G-оптимальные планы определяются как планы, минимизирующие максимальное значение стандартной ошибки предсказания отклика. Построение оптимальных планов


Построение оптимальных планов

Средства построения оптимальных планов в модуле Планирование эксперимента будут “осуществлять поиск” оптимальные планы при заданном списке “точек-кандидатов”. Иными словами, при заданном списке точек, определяющих допустимую область, и определенном пользователем числе опытов окончательного эксперимента, программа будет отбирать точки для оптимизации соответствующего критерия. Этот “поиск” наилучшего плана не точный метод, а алгоритмическая процедура, использующая некоторые стратегии поиска для нахождения наилучшего плана (согласно некоторому критерию оптимальности).

Предложенные процедуры и алгоритмы поиска описаны ниже (для обзора и подробного сравнения, смотрите работу Cook и Nachtsheim, 1980). Они расположены в порядке скорости реализации: Последовательный метод или метод Дейкстры является наиболее быстрым, но часто приводит к неправильному результату, то есть к плану, не являющемуся оптимальным (например, строится только локально оптимальный плану, вопрос о котором будет коротко обсужден далее).

Последовательный метод или метод Дейкстры. Этот алгоритм принадлежит Дейкстре (Dykstra, 1971). Начиная с пустого плана, программа ведет поиск по списку точек-кандидатов и на каждом шаге отбирает одну, которая максимизирует выбранный критерий. Не проводятся итерации, программа просто последовательно отбирает заданное число точек. Таким образом, этот метод самый быстрый из обсуждаемых. Кроме того, по умолчанию, этот метод используется остальными для построения начального плана.

Метод простого обмена (Винна-Митчелла).
Метод простого обмена (Винна-Митчелла).

Этот алгоритм обычно приписывают работам Mitchell и Miller (1970) и Wynn (1972). Метод стартует с начального плана требуемого объема (по умолчанию строящийся с помощью алгоритма последовательного поиска, описанного выше). В каждой итерации одна точка (опыт) выбрасывается из плана, а одна – добавляется из списка кандидатов. Выбор точек для выбрасывания и добавления последовательный, то есть на каждом шаге точка, добавляющая меньше всего относительно выбранного критерия оптимальности выбрасывается из плана, затем алгоритм отбирает точку из списка кандидатов для максимального увеличения соответствующего критерия.


Алгоритм останавливается, когда нет дальнейшего улучшения с помощью дополнительных изменений.

Алгоритм DETMAX (обмен с отклонениями). Этот алгоритм принадлежащий Митчеллу (Mitchell, 1974b), вероятно наилучший из известных и наиболее широко используемый для поиска оптимального плана. Подобно алгоритму простого обмена (Винна-Митчелла) вначале строится исходный план (по умолчанию с помощью алгоритма последовательного поиска, описанного выше). Поиск начинается с применения алгоритма простого обмена (Винна-Митчелла), как описано выше. Однако, если соответствующий критерий (D или A) не улучшается, алгоритм предпринимает отклонения. А именно, алгоритм добавляет или выбрасывает более одной точки за один раз, так что во время поиска число точек в плане может изменяться между ND+ Nотклонение и ND+ Nотклонение, где ND – требуемый объем плана, а Nотклонение обозначает максимально допустимое отклонение, определяемое пользователем. Итерации останавливаются, когда выбранный критерий (D или A) больше не улучшается с помощью максимального отклонения.

Модифицированный алгоритм Федорова (одновременного переключения). Этот алгоритм представляет модификацию (Cook и Nachtsheim, 1980) основного алгоритма Федорова, описанного ниже. Он также начинается с исходного плана требуемого объема (по умолчанию строящегося с помощью алгоритма последовательного поиска). На каждой итерации алгоритм обменивается каждой точкой плана с отобранной из списка точек-кандидатов, чтобы оптимизировать план согласно выбранному критерию (D или A). В отличие от алгоритма простого обмена (Винна-Митчелла) алгоритм, описанного выше, в данном алгоритме обмен не последовательный, а одновременный. Так, на каждой итерации каждая точка плана сравнивается с каждой точкой из списка кандидатов, и обмен происходит парой, оптимизирующей план. Алгоритм останавливается, когда нет дальнейшего улучшения соответствующего критерия оптимальности.

Алгоритм Федорова (одновременного переключения).
Алгоритм Федорова (одновременного переключения).



Этот оригинальный метод одновременного переключения предложен В.В.Федоровым (см. Cook и Nachtsheim, 1980). Отличие данной процедуры от процедуры, описанной выше (модифицированный алгоритм Федорова), заключается в том, что на каждой итерации осуществляется только единственный обмен, то есть на каждой итерации оцениваются все возможные пары точек плана и списка кандидатов. Алгоритм обменивается парой, оптимизирующей план относительно выбранного критерия. Таким образом, этот алгоритм потенциально может быть весьма медленным, поскольку на каждой итерации осуществляется ND*NC сравнений для обмена единственной точкой. Общие рекомендации
Общие рекомендации

Если вы подумаете над основными стратегиями поиска, представленных различными алгоритмами, описанными выше, станет ясно, что не существует точного решения проблемы оптимального плана. Именно, детерминант матрицы X’X (и след ее обратной) являются сложными функциями списка точек-кандидатов. В частности, имеется несколько “локальных минимумов” относительно выбранного критерия оптимальности, например, в любой момент поиска план может казаться оптимальным, до тех пор, пока вы одновременно не выбросите половину точек плана и не выберете некоторые другие точки из списка кандидатов, но если вы обмениваетесь отдельными точками или только несколькими точками (как в алгоритме DETMAX), тогда улучшения не случится.

Следовательно, важно попробовать ряд начальных планов и несколько алгоритмов. Если после повторения оптимизации несколько раз со случайного старта получится тот же самый или близкий оптимальный план, тогда вы можете быть в достаточной мере уверены, что вы не “попали” в локальный минимум или максимум.

Кроме того, методы, описанные выше, сильно различаются способностью “попадания” в локальные минимумы или максимумы. Общее правило состоит в том, что чем медленнее алгоритм (то есть чем он ниже в списке, описанном выше), тем более вероятно, что он приведет к истинно оптимальному плану. Однако, заметим, что модифицированный алгоритм Федорова практически работает так же хорошо, как и не модифицированный алгоритм (смотрите Cook и Nachtsheim, 1980); следовательно, если не рассматривать фактор времени, мы рекомендуем модифицированный алгоритм Федорова как наилучший для практического использования.



D-оптимальность и A-оптимальность.
D-оптимальность и A-оптимальность.

По вычислительным соображениям (смотрите Galil и Kiefer, 1980), обновление следа матрицы (для критерия A-оптимальности) много медленнее, чем обновление детерминанта (для D-оптимальности). Так что, если вы выбираете критерий A-оптимальности, вычисления могут занимать значительно больше времени по сравнению с критерием D-оптимальности. Поскольку на практике имеется много других факторов, влияющих на качество эксперимента, (например, надежность измерения зависимой переменной), мы, вообще говоря, рекомендуем использование критерия D-оптимальности. Однако, в трудных ситуациях построения плана, например, когда выясняется, что имеется много локальных максимумов критерия D, и повторные попытки приводят к сильно различающимся результатам, вы можете попробовать несколько прогонов оптимизации критерия A , чтобы лучше изучить различные типы возможных планов. Устранение вырожденности матрицы
Устранение вырожденности матрицы

Может оказаться, что в процессе поиска, программа не сможет вычислить обратную матрицу к X’X матрица (для A-оптимальности) или, что детерминант матрицы становится близок к 0 (нулю). В этом случае поиск обычно не может продолжаться. Чтобы избежать подобной ситуации, программа осуществляет оптимизацию, основываясь на подправленной матрице X’X :

X'Xaugmented = X'X + *(X0'X0/N0)

где X0 обозначает матрицу плана, построенную из списка N0 всех точек-кандидатов, а where X0 stands for the design matrix constructed from the list of all N0 candidate points, and (альфа) – определяемая пользователем малая константа. Так, вы можете использовать это свойство, положив (alpha) is a user-defined small constant. Thus, you can turn off this feature by setting = 0 (нулю).


“Подправление” планов
“Подправление” планов

Свойства оптимальных планов могут быть использованы для “подправления” планов. Например, предположим, что вы используете ортогональный план, но некоторые данные потеряны (например, из-за неисправности оборудования), и вследствие этого некоторые интересующие вас эффекты не могут быть оценены.


Вы, конечно, можете переделать потерянные опыты, но, предположим, что у вас нет ресурсов для того, чтобы переделать их все. В этом случае вы можете построить список точек-кандидатов из всех подходящих для этого точек экспериментальной области, добавить к этому списку все точки, для которых вы уже проделали опыты, и проинструктировать программу всегда включать эти точки в окончательный план (и никогда их не исключать, то есть вы можете пометить их в списке кандидатов с помощью опции непременного (насильственного) включения). Теперь можно исключать из плана лишь те точки, в которых вы пока не ставили опытов. Подобным образом вы можете, например, найти единственный опыт, добавив который к эксперименту, вы оптимизируете соответствующий критерий. Ограниченные экспериментальные области и оптимальный план
Ограниченные экспериментальные области и оптимальный план

Типичным применением оптимального плана являются ситуации, когда интересующая нас экспериментальная область ограничена. Как описано ранее в этом разделе, существуют средства и возможности для нахождения вершин и центроидов в случае областей с линейными ограничениями и для смесей. Такие точки могут затем быть представлены в списке точек-кандидатов для построения оптимального плана заданного объема для конкретной модели. Таким образом, эти два свойства, будучи объединены, предоставляют очень мощное средство справиться с трудными ситуациями построения плана, когда интересующая нас область подвергнута сложным ограничениям, а мы желаем подогнать конкретную модель при наименьшем числе опытов.

В начало

Специальные разделы
Специальные разделы



Последующие разделы описывают некоторые методы анализа: Профили отклика/функции желательности, проведение Анализа остатков и выполнение Преобразования Бокса-Кокса зависимых переменных.

Смотрите также Дисперсионный анализ, Методы дисперсионного анализа и Компоненты дисперсии и смешанные модели ANOVA/ANCOVA. Создание профиля предсказанного и желательного отклика
Создание профиля предсказанного и желательного отклика



Основная идея.
Основная идея.

Типовая задача, часто решаемая на производстве, заключается в поиске набора условий или уровней входных переменных, которые позволяют получить продукт с наилучшими характеристиками, т.е. с наилучшими значениями переменных отклика. Процедуры, используемые для решения этой задачи обычно включают два шага: (1) предсказание отклика, т.е значений зависимых Y-переменных, с помощью подгонки моделирующего уравнения на основе имеющихся данных об отклике на заданных уровнях независимых X-переменных, (2) поиск уровней X-переменных, которые одновременно дают наиболее желательные предсказанные отклики Y-переменных. Derringer и Suich (1980) предложили в качестве примера этих процедур задачу нахождения состава ткани, наиболее устойчивого к истиранию. В ней даны такие переменные Y, как PICO показатель истирания, 200-процентный модуль, продолжительность воздействия и плотность. Характеристики продукта в терминах переменных отклика зависят от состава, переменных X, таких как hydrated silica level – доля гидрата кварца, silane coupling agent level – доля соединения силана и sulfur. Задача состоит в нахождении уровней переменных X, которые максимизируют желательность откликов Y. Решение должно учитывать тот факт, что уровни переменных X, которые максимизируют один отклик, могут не максимизировать другой отклик.

Профиль отклика/функции желательности в анализе таких планов, как 2**(k-p) (двухуровневые факторные) планы, 2-х уровневые отсеивающие планы, Максимально несмешанные 2**(k-p) планы, Планы 3**(k-p) и планы Бокса-Бенкена, Смешанные 2-х и 3-х уровневые планы, Центральные композиционные планы и Планы для смесей позволяет вам просматривать поверхность отклика, получаемую при подгонке наблюдаемых откликов с использованием уравнения, основанного на уровнях независимых переменных.

Профили предсказания. Когда вы анализируете результаты любого из перечисленных выше планов, для подгонки наблюдаемых откликов каждой зависимой переменных (содержащих различные коэффициенты, но одинаковые члены) используются отдельные уравнения предсказания.


Как только эти уравнения построены, предсказанные значения для зависимых переменных могут быть вычислены для любой комбинации уровней предикторов. Профиль предсказания для зависимой переменной состоит из серии графиков, по одному на каждую независимую переменную (предиктор), предсказанных значений зависимой переменной при различных уровнях независимой переменной, при значениях других независимых переменных, равных константе на заданных уровнях, называемых текущими значениями. Если выбраны соответствующие текущие значения для независимых переменных, просмотр профиля предсказания поможет выяснить, какие уровни предикторов дают наиболее желательный отклик зависимой переменной.

Исследователь может быть заинтересован в контроле предсказанных значений зависимых переменных только на текущих уровнях, которые принимают независимые переменные в течение эксперимента. В качестве альтернативы, исследователь может быть заинтересован в контроле предсказанных значений зависимых переменных на уровнях, отличных от текущих уровней независимых переменных, используемых в течение эксперимента, в целях выявления промежуточных уровней независимых переменных, которые могут дать даже более желательные отклики. Также, возвращаясь к примеру Derringer и Suich (1980), для некоторых переменных отклика наиболее желательные значения не обязательно являются наиболее экстремальными значениями, например, наиболее желательное значение продолжительности воздействия может лежать в узком диапазоне возможных значений.

Желательность отклика. Разные зависимые переменные могут по-разному зависеть от различных взаимосвязей между вкладами переменной и желательностью вкладов. Более светлое пиво может быть более желательным, но более вкусное пиво также может быть более желательным: оба свойства - большей "светлости" и большей "вкусности" - более желательны. Взаимосвязь между предсказанными откликами зависимой переменной и желательностью откликов называется функцией желательности. Derringer и Suich (1980) выработали процедуру для определения взаимосвязи между предсказанными откликами зависимой переменной и желательностью откликов, процедуру, которая предполагает до трех точек "перегиба" функции.


Применительно к примеру по составу ткани, описанного выше, эти процедуры включают преобразование вкладов каждой из четырех результирующих переменных, характеризующих состав ткани, в желательности вкладов, которые находятся в интервале от 0.0 для нежелательных до 1.0 для очень желательных. Например, их функция желательности для hardness - плотности состава ткани определяется заданием значения желательности 0.0 для показателя hardness, меньшего 60 или большего 75, значения желательности 1.0 для срединного показателя hardness 67.5, значения желательности, увеличивающегося линейно от 0.0 до 1.0 для показателей hardness между 60 и 67.5 и значения желательности, уменьшающегося линейно от 1.0 до 0.0 для показателей hardness между 67.5 и 75.0. В более общем смысле это означает, что процедуры нахождения функций желательности должны обеспечивать кривизну "уменьшения" желательности между точками перегиба функции.

После преобразования предсказанных значений зависимых переменных при различных комбинациях уровней предикторных переменных в индивидуальные показатели желательности может быть вычислена общая желательность исходов при различных комбинациях уровней предикторных переменных. Derringer и Suich (1980) предложили вычислять общую желательность как геометрическое среднее отдельных желательностей (что имеет интуитивно понятный смысл, так как, если отдельная желательность некоторого исхода равна 0.0, или нежелательна, общая желательность тоже будет равна 0.0, или нежелательна, не учитывая при этом, насколько желательны другие отдельные исходы — геометрическое среднее берет произведение всех значений и возводит это произведение в степень, обратную числу значений). Процедура Derringer и Suich дает простой способ преобразования предсказанных значений для множественных зависимых переменных в простой показатель общей желательности. Проблема одновременной оптимизации нескольких переменных отклика затем сводится к выбору уровней предикторных переменных, которые максимизируют общую желательность откликов зависимых переменных.



Выводы. Когда исследователь разрабатывает продукт, для которого известно, что его свойства зависят от его "ингредиентов", создание лучшего продукта, возможно, требует определения эффектов его ингредиентов на каждое свойство продукта в отдельности и последующее нахождение гармонического сочетания ингредиентов, оптимизирующего общую желательность продукта. В терминах анализа данных, процедура, которая производит максимизацию желательности продукта, делает следующее: (1) находит адекватные модели (т.е. уравнения предсказания) для предсказания свойств продукта как функцию уровней независимых переменных, и (2) определяет оптимальные уровни независимых переменных для получения высокого общего качества продукта. Эти два шага, если им точно следовать, с большой вероятностью приводят к большему успеху в усовершенствовании продукта, чем придуманная, но статистически сомнительная методика надежды на случайные достижения и открытия, которые радикально улучшили бы качество продукта.

Анализ остатков
Анализ остатков

Основная идея.
Основная идея.

Расширенный анализ остатков - это ряд диагностических средств для контроля различных остаточных и предсказанных значений, проверки адекватности модели предсказания, необходимости преобразований переменных модели, и наличия выбросов в данных.

Остатки – это отклонения наблюдаемых значений зависимой переменной от предсказанных значений, получаемых текущей моделью. Модели ANOVA, используемые в анализе откликов зависимой переменной, делают некоторые предположения о виде распределения остатков (но не предсказанных значений) зависимой переменной. Эти предположения можно выразить, сказав, что модель ANOVA предполагает нормальность, линейность, постоянство дисперсии и независимость остатков. Эти свойства остатков для зависимой переменной могут быть проверены с помощью Статистик остатков.

Преобразование Бокса-Кокса зависимых переменных
Преобразование Бокса-Кокса зависимых переменных

Основная идея.
Основная идея.

В дисперсионном анализе делается предположение, что дисперсии различных групп (состояний эксперимента) однородны, и что они не коррелированы со средними.


Если распределение значений в каждом состоянии асимметрично, и если средние коррелированы со стандартными отклонениями, то исследователь часто может применить соответствующее степенное преобразование зависимой переменной для стабилизации дисперсий, а также для уменьшения или устранения корреляции между средними и стандартными отклонениями. Преобразование Бокса-Кокса используется для выбора соответствующего (степенного) преобразования зависимой переменной.

Опция Преобразование Бокса-Кокса выдает график Остаточной суммы квадратов, даваемой моделью, как функции значения лямбда, где лямбда используется для задания преобразования зависимой переменной,

y' = ( y**(lambda) - 1 ) / ( g**(lambda-1) * lambda)	if lambda 0
y' = g * natural log(y)	if lambda = 0

где g обозначает геометрическое среднее зависимой переменной, и все значения зависимой переменной неотрицательны. Значение лямбда, для которого Остаточная сумма квадратов минимальна, является оценкой максимального правдоподобия для этого параметра. Это дает стабилизирующее дисперсию преобразование зависимой переменной, которое уменьшает или исключает корреляцию между групповыми средними и стандартными отклонениями.

На практике нет необходимости использовать точно оцененное значение лямбда для преобразования зависимой переменной. Предпочтительнее, как эмпирическое правило, рассматривать следующие преобразования:

Approximate
lambda Suggested
transorfmation of y

-1    -0.5  0     0.5  1	Reciprocal Reciprocal square root Natural logarithm Square root None

За дополнительной информацией по этому семейству преобразований обращайтесь к Box и Cox (1964), Box и Draper (1987) и Maddala (1977).

В начало

© Copyright StatSoft, Inc., 1984-2001
STATISTICA is a trademark of StatSoft, Inc.

В этом разделе рассматриваются решения

Примеры проектов, реализованных  на STATISTICA