Порядок выполнения факторного анализа

19.1 Порядок выполнения факторного анализа

На первом шаге процедуры факторного анализа происходит стандартизация заданных значений переменных (z-преобразование); затем при помощи стандартизированных значений рассчитывают корреляционные коэффициенты Пирсона между рассматриваемыми переменными.

Исходным элементом для дальнейших расчётов является корреляционная матрица. Для понимания отдельных шагов этих расчётов потребуются хорошие знания, прежде всего, в области операций над матрицами; интересующимся подробностями советуем обратиться к специальной литературе. Для построенной корреляционной матрицы определяются, так называемые, собственные значения и соответствующие им собственные векторы, для определения которых используются оценочные значения диагональных элементов матрицы (так называемые относительные дисперсии простых факторов).

Собственные значения сортируются в порядке убывания, для чего обычно отбирается столько факторов, сколько имеется собственных значений, превосходящих по величине единицу. Собственные векторы, соответствующие этим собственным значениям, образуют факторы; элементы собственных векторов получили название факторной нагрузки. Их можно понимать как коэффициенты корреляции между соответствующими переменными и факторами. Для решения такой задачи определения факторов были разработаны многочисленные методы, наиболее часто употребляемым из которых является метод определения главных факторов (компонентов).

Описанные выше шаги расчёта ещё не дают однозначного решения задачи определения факторов. Основываясь на геометрическом представлении рассматриваемой задачи, поиск однозначного решения называют задачей вращения факторов. И здесь имеется большое количество методов, наиболее часто употребляемым из которых является ортогональное вращение по так называемому методу варимакса. Факторные нагрузки повёрнутой матрицы могут рассматриваться как результат выполнения процедуры факторного анализа. Кроме того на основании значений этих нагрузок необходимо попытаться дать толкование отдельным факторам.

Если факторы найдены и истолкованы, то на последнем шаге факторного анализа, отдельным наблюдениям можно присвоить значения этих факторов, так называемые факторные значения. Таким образом для каждого наблюдения значения большого количества переменных можно перевести в значения небольшого количества факторов.

Пример из области социологии

19.2 Пример из области социологии

Изложенный метод будет проиллюстрирован на примере анкеты, составленной в Институте Социологии Университета Марбург. На основе этой анкеты на двух гессенских металлургических предприятиях было произведено исследование отношения к иностранцам. Опрашиваемым предложили высказать свое отношение к следующим пятнадцати положениям:

1. Необходимо улучшить интеграцию иностранцев.

2. Необходимо мягче относиться к беженцам.

3. Деньги Германии должны быть потрачены на нужды страны.

4. Германия — это не служба социальной помощи для всего мира.

5. Необходимо стараться налаживать хорошие отношения друг с другом.

6. Права беженцев следует ограничить.

7. Немцы станут меньшинством.

8. Право беженцев необходимо охранять во всей Европе.

9. Враждебность к иностранцам наносит вред экономике Германии.

10. Сначала необходимо создать нормальные жилищные условия для немцев.

11. Мы ведь тоже практически везде являемся иностранцами.

12. Мультикультура означает мультикриминал.

13. В лодке нет свободных мест.

14. Иностранцы вон.

15. Интеграция иностранцев — это убийство нации.

Оценки ставились по семибальной шкале: от полного несогласия (1) до полного согласия (7). Результаты опроса для 90 человек хранятся в файле ausland.sav в переменных а1-а15.

Откройте файл ausland.sav. В файле Вы заметите несколько дополнительных переменных, о которых мы расскажем позже.

Выберите в меню Analyze (Анализ) Data Reduction (Сокращение объема данных) Factor... (Факторный анализ)

Откроется диалоговое окно Factor Analysis (Факторный анализ) (см. рис. 19.1).

Пример из области психологии

19.3 Пример из области психологии

В анкете изучения вариантов поведения при заболевании по пунктам описываются возможные варианты поведения, дающие объяснение отношения больных к их болезни. На основании пятибалльной шкалы, балы которой соответствуют выражениям: абсолютно не подходит (1) —- незначительно (2) — умеренно (3) — довольно значительно (4) — и очень сильно (5), психолог должен понять, насколько сильно указанная ситуация подходит их пациенту. Помимо этого, посредством факторного анализа необходимо будет ещё определить, можно ли пункты анкеты логически связать с факторами, которые дают объяснение возможной типологии отношения к болезни. Сначала рассмотрим пункты стандартной анкеты:

1. Искать информацию о заболевании и лечении

2. Не желать признать случившееся

3. Занижать значение и важность болезни

4. Размышлять и мечтать о своём

5. Винить самого себя

6. Считать виноватыми других

7. Предпринимать активные действия для решения проблемы

8. Составить план и затем приступить к действиям

9. С нетерпением и раздражённо на всё реагировать

10. Выносить все эмоции наружу

П. Подавлять эмоции, проявлять самообладание

12. Искать улучшение настроения в употреблении алкоголя или успокаивающих средств

13. Больше себе позволять

14. Пытаться интенсивней жить

15. Решиться на борьбу с болезнью

16. Жалеть себя

17. Подбадривать себя

18. Пытаться достичь успеха и самоутверждения

19. Пытаться отвлечься

20. Искать уединения

21. Принимать болезнь как судьбу

22. Впасть в бесконечные размышления

23. Искать утешения в религии

24. Пытаться найти какой-либо смысл в болезни

25. Утешать себя тем, что другим ещё хуже

26. Ссылаться на судьбу

27. Точно следовать указаниям врача

28. Надеяться на врачей

29. Не доверять врачам, перепроверять диагноз, искать других врачей

30. Желать делать добро другим

31. Изображать напускное веселье

32. Принимать помощь от других

33. Позволять о себе заботиться

34. Отдаляться от других людей

35. Пытаться припомнить личный опыт и методы борьбы с подобными ударами судьбы

Результаты для 160 пациентов хранятся в файле fkv.sav в переменных fl-f35.

Откройте файл fkv.sav

Выберите в меню Analyze (Анализ) Data Reduction (Сокращение объема данных) Factor... (Факторный анализ)

Откроется диалоговое окно Factor Analysis (Факторный анализ) (см. рис. 19.1). Поместите переменные П-О5 в поле тестируемых переменных.

Щёлкните на выключателе Descriptives... (Дескриптивные статистики). Откроется диалоговое окно Factor Analysis: Descriptives (Факторный анализ: Дескриптивные статистики), как представлено на рисунке 19.2. Оставьте установленную по умолчанию опцию вывода Initial solution (Первичного решения).

Щёлкните на выключателе Extraction... (Извлечение), оставьте установку Principal components (Анализ главных компонентов). В отличие от первого примера факторного анализа, здесь количество факторов сознательно ограничим пятью. Если бы мы не сделали такого ограничения, то в соответствии с начальными установками было бы создано одиннадцать факторов, количество, которое очень тяжело поддаётся обзору.

Задача вращения

19.4 Задача вращения

Рассмотрим поподробнее задачу вращения. Используем для этого приводившийся в разделе 19.2 пример опроса, исследующего отношение к иностранцам.

Откройте файл ausland.sav.

Выберите в меню Analyze (Анализ) Data Reduction (Сокращение объема данных) Factor... (Факторный анализ)

В диалоговом окне Factor Analysis (Факторный анализ) поместите переменные al-а!5 в поле тестируемых переменных.

С помощью кнопки Extraction... (Извлечение) укажите требуемое число создаваемых факторов равное двум, чтобы получить легко интерпретируемый двумерный пример.

Через выключатель Rotation... (Вращение) активируйте опцию Loading plot(s) (Диаграмма нагрузок), но для модели вращения оставьте установленную по умолчанию опцию None (Отсутствует).

В результате мы оставляем вывод так называемой компонентной диаграммы.

Диалоговое окно Factor Analysis: Descriptives (Факторный анализ: Дескриптивные статистики)

Щёлкните поэтому на опции Number of factors (Количество факторов) и введите число 5. Щелчком на соответствующей опции деактивируйте вывод неповёрнутых значений факторов. Активируйте опцию Scree plot (Точечная диаграмма). Точечная диаграмма графически представляет собственные значения факторов, упорядоченные по величине.

Диалоговое окно Factor Analysis:Extraction < Факторный анализ: Извлечение) должно теперь выглядеть так, как представлено на рисунке 19.3.

Диалоговое окно Factor Analysis: Extraction (Факторный анализ: Отбор)

Подтвердите произведенные установки нажатием Continue (Далее). Щёлкните на выключателе Rotation... (Вращение) и выберите метод варимакса. Если вы желаете наряду с выводом повёрнутой матрицы факторов, установленным по умолчанию, получить факторные нагрузки в графическом виде, то щёлкните на опции Loading plot(s) (Диаграммы нагрузок). Диалоговое окно Factor Analysis:Rotation (Факторный анализ: Вращение) должно теперь выглядеть так, как изображено на рисунке 19.4.

Подтвердите нажатием кнопки Continue (Далее). Щёлкните по выключателю Scores... (Значения) и активируйте Save as variables (Сохранить как переменные), чтобы рассчитанные значения факторов сохранить в виде дополнительных переменных. Диалоговое окно Factor AnalysisiFactor Scores (Факторный анализ: Значения факторов) выглядит теперь так, как изображено на рисунке 19.5.

Диалоговое окно Factor Analysis:Factor Scores (Факторный анализ: Значения факторов)

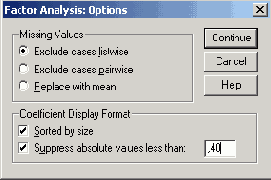
Теперь мы запретим вывод малых факторных нагрузок и для этого установим граничное значение выводимых нагрузок равным 0,4. Достоинство этого шага состоит в том, что устраняется непривлекательное отображение малых значений в Е-формате (см. раздел 19.2).

Активируйте опцию Suppress absolute values less then: (He выводить абсолютные значения меньшие, чем:) и введите предельное значение 0,4.

Диалоговое окно Factor Analysis:0ptions (Факторный анализ: Опции) выглядит теперь так, как изображено на рисунке 19.6.

Для проведения факторного анализа подтвердите произведенные установки нажатием Continue (Далее) и в главном диалоговом окне ОК.

Рассмотрит результаты расчёта, которые появились в окне просмотра. Сначала приводятся первичные статистики.

Диалоговое окно Factor Analysis (Факторный анализ)

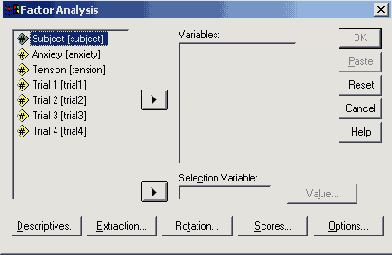
Переменные a1-a15 поместите в поле тестируемых переменных и ознакомьтесь с возможностями, предлагаемыми различными кнопками этого диалогового меню.

После щелчка по кнопке Descriptive Statistics (Дескриптивные статистики) оставьте вывод первичных результатов, которые включают в себя первичные относительные дисперсии простых факторов, собственные значения и процентные доли объяснённой дисперсии. Довольно часто бывает необходим также вывод одномерных статистик и корреляционных коэффициентов.

С помощью кнопки Extraction... (Отбор) Вы можете выбрать метод отбора; оставьте здесь анализ главных компонентов, установленный по умолчанию. Количество отобранных в этом случае факторов приравнивается к числу собственных значений, превосходящих единицу. У Вас также есть возможность собственноручно указать это количество. Так как неповёрнутое факторное решение, предоставляет малозначимую информацию, предотвратите его вывод щелчком на соответствующей опции.

Выключатель Rotation... (Вращение) позволяет выбрать метод вращения. Активируйте метод варимакса и оставьте активированным вывод повёрнутой матрицы факторов. Далее вы можете организовать вывод факторных нагрузок в графическом виде, в котором первые три фактора будут представлены в трёхмерном пространстве; в случае наличия только двух факторов в слое приводится только одно изображение.

Если Вы хотите найти значения факторов и сохранить их в виде дополнительных переменных задействуйте выключатель Scores... (Значения) и отметьте Save as variables (Сохранить как переменные). По умолчанию установлен регрессионный метод. Выключатель Options... (Опции) предназначен для обработки пропущенных значений. Здесь обеспечивается возможность заменить пропущенные значения средними значениями соответствующих переменных.

Для проведения расчётов щёлкните на ОК.

В окне обзора появятся результаты. Сначала приводятся первичные статистики:

Total Variance Explained

(Объяснённая суммарная дисперсия)
Compo-nent (Компо-ненты)	Initial Eigenvalues (Первичные собственные значения)	Rotation Sums of Squared Loadings (Повёрнутые суммы квадратов нагрузок)
Total (Сумма)	% of Variance (% диспе-рсии)	Cumulative % (Сово-купный %)	Total (Сум-ма)	% of Variance (% дис-персии)	Cumu-lative % (Сово-купный %)
1	5,146	34,308	34,308	3,466	23,105	23,105
2	1,945	12,970	47,278	2,536	16,907	40,013
3	1,415	9,433	56,711	2,505	16,698	56,711
4	,990	6,601	63,312
5	,936	6,238	69,550
6	,760	5,068	74,617
7	,693	4,622	79,240
8	,612	4,083	83,323
9	,529	3,529	86,852
10	,473	3,151	90,004
11	,433	2,889	92,893
12	,339	2,262	95,1555
13	,301	2,007	97,161
14	,245	1,635	98,797
15	,181	1,203	100,000

Extraction Method: Principal Component Analysis (Метод отбора: Анализ главных компонентов).

По таблице можно увидеть, что три собственных фактора имеют значения превосходящие единицу. Следовательно для анализа отобрано только три фактора. Первый фактор объясняет 34,308 % суммарной дисперсии, второй фактор 12,97 % и третий фактор 9,433 %. Так как мы запретили вывод неповернутой матрицы факторов, то далее приводится повёрнутая матрица (см. следующую таблицу).

При факторном анализе постоянно появляются сообщения об ошибках, — так нам жаловался один пользователь, — например 2,56Е-02 и т.п. Действительно такой формат вывода в глазах непосвященного пользователя очень портит картину всей таблицы. Это, так называемый, Е-формат, знакомый всем программистам по языку Фортран (Fortran), где буква Е соответствует 10 в некоторой степени; для числа 2,5Е-02 можно было бы записать и 0,0256. Во втором примере (гл. 19.3) мы покажем Вам, как выходить из такой ситуации.

Rotated Component Matrix a

(Повёрнутая матрица компонентов)
	Component (Компонент)
1	2	3
А1	-,466	,628	-,191
А2	-,141	,657	,215
A3	,327	-,153	,711
А4	,533	-,106	,394
А5	-,362	,783	4.52Е-02
А6	-1.2Е-02	-3.8Е-02	,763
А7	,525	3.58Е-02	,543
А8	-,117	,719	-,267
А9	2.56Е-02	,551	-8.8Е-02
А10	,252	-9.5Е-02	,685
А11	,125	,392	-,292
А12	,802	-,199	,108
А13	,685	-,110	,465
А14	,837	-,144	-2.5Е-02
А15	,725	-4.8Е-02	,144

Extraction Method: Principal Component Analysis ((Метод отбора: Анализ главных компонентов).

Rotation Method: Varimax with Kaiser Normalization (Метод вращения: Варимакс с нормализацией Кайзера),

a. Rotation converged in 8 iterations (Вращение осуществлено за 8 итераций).

Здесь начинается самая интересная часть факторного анализа: Вы должны попытаться объяснить отобранные факторы. Для этого возьмите в руки карандаш и в каждой строке повёрнутой факторной матрицы отметьте ту факторную нагрузку, которая имеет наибольшее абсолютное значение.

Как уже было сказано, эти факторные нагрузки следует понимать как корреляционные коэффициенты между переменными и факторами. Так переменная a1 сильнее всего коррелирует с фактором 2, а именно, величина корреляции составляет 0,628, переменная а2 также сильнее всего коррелирует с фактором 2 (0,657), переменная же а3 коррелирует сильнее всего с фактором 3 (0,711) и т.д. В большинстве случаев включение отдельной переменной в один фактор, осуществляемое на основе коэффициентов корреляции, является однозначным. В исключительных случаях, к примеру, как в ситуации с переменной а7, переменная может относиться к двум факторам одновременно. Могут быть также и переменные, в нашем примере a11, которыми нельзя нагрузить ни один из отобранных факторов.

Если поступить так, как изложено выше, то варианты мнений, указанные вначале рассмотрения примера, можно отнести в следующем порядке к трём факторам:

Фактор 1:

Германия — это не служба социальной помощи для всего мира.

Немцы станут меньшинством.

Мультикультура означает мультикриминал.

В лодке нет свободных мест.

Иностранцы вон.

Интеграция иностранцев — это убийство нации.

Фактор 2

Необходимо улучшить интеграцию иностранцев.

Необходимо мягче относиться к беженцам.

Необходимо стараться налаживать хорошие отношения друг с другом.

Права беженцев необходимо охранять во всей Европе.

Враждебность к иностранцам наносит вред экономике Германии.

Мы ведь тоже практически везде являемся иностранцами.

Фактор 3

Деньги Германии должны быть потрачены на нужды страны.

Права беженцев следует ограничить.

Немцы станут меньшинством.

Сначала необходимо создать нормальные жилищные условия для немцев.

Из-за равных по величине нагрузок, как для фактора 3, так и для фактора 1, положение "Немцы станут меньшинством" включено в оба фактора. Теперь мы подошли к последнему и решающему шагу факторного анализа: необходимо обнаружить и описать смысловую связь факторов. В рассматриваемом примере это можно сделать без особых усилий.

Первый фактор, и это очевидно, собрал все положения, враждебно настроенные по отношению к иностранцам. На основании позитивных корреляционных коэффициентов участвующих переменных с фактором и принимая во внимание полярность значений переменных (большое значение означает полное согласие) большое значение фактора означает высокую враждебность к иностранцам.

Во второй фактор входят те положения, которые указывают на дружелюбное отношение к иностранцам. Большое значение фактора означает здесь доброжелательное отношение к иностранцам.

Во второй фактор вошли точки зрения, соответствующие осторожному отношению к иностранцам; в противоположность к первому фактору это не враждебные точки зрения, а по большей части социальные страхи (деньги, жильё в первую очередь для немцев и т.д.). Большое значение фактора указывает здесь на высокую степень социального сомнения.

В соответствии с порядком изложения эти три фактора можно кратко охарактеризовать при помощи следующих выражений: Враждебная позиция, Доброжелательная позиция и Социальные страхи. Однако столь явно, как в приведенном примере факторы удаётся объяснить не всегда. Если нет возможности провести вербальное объяснение факторов, то факторный анализ можно считать неудавшимся.

Значения факторов

Поскольку мы пожелали произвести расчёт значений факторов, то в соответствии с тремя отобранными факторам были сгенерированы три новые переменные, на-

званные fac1_1, fac2_1 и fac3_1, которые содержат вычисленные значения факторов. Если Вы просмотрите текущий файл после поведения факторного анализа, то сможете увидеть имеющие нормализованные значения факторов. По каждому из отобранных фактору для каждого опрошенного было рассчитано специальное факторное значение. Факторное значение, как правило, лежит в пределах —3 до +3.

Рассмотрим факторную переменную fac1_1. Она включает следующие элементарные переменные: а4, а12, а13, а14 и а15. В качестве метки для этого фактора мы выбрали выражение: "Враждебная позиция". Большое положительное значение фактора означает одобрение элементарных переменных, то есть положений, входящих в этот фактор. Одобрение элементарных переменных, относящихся к первому фактору, тождественно ярко выраженным расистским взглядам. Для подтверждения этого факта рассмотрим два примера. Наблюдение 4 характеризуется очень низким факторным значением в переменной fac1_1. Оно равно —2,00455. В данном случае можно сделать заключение о том, что здесь не наблюдается расистская направленность или она очень слаба. Соответственно этому ведут себя и отдельные значения элементарных переменных (а4 = 2, а13 = 1, а14 = 1, а15 = 1). Наблюдение 17, в отличие от наблюдения 4, характеризуется очень высоким положительным значением фактора, который равен 3,14801. Основываясь на этом значении, мы можем исходить из того, что здесь явно заметна экстремально-расистская позиция. Соответственно этому ведут себя и отдельные значения элементарных переменных (а4 = 7, а13 = 7, а14 = 7, а15 = 7).

Рассмотрим факторную переменную fac2_1. К ней относятся элементарные переменные: a1, a2, а5, а8, а9 и a11. В качестве метки для этого фактора мы выбрали выражение: "Доброжелательная позиция". Большое положительное значение фактора означает полное согласие. Полное согласие соответствует дружелюбному отношению к иностранцам. И здесь рассмотрим два выборочных примера. Наблюдение 17 характеризуется очень малым значением фактора, которое составляет —3,32632. Основываясь на значении этого фактора можно сделать вывод, что едва ли в этом случае присутствует доброжелательное отношение к иностранцам. Соответственным образом ведут себя и отдельные значения элементарных переменных (a1 = 1, а2 = 1, а5 = 1, а8 = 2, а9 = 4, a11 = 6). В наблюдении 17 и следовало ожидать низкого значения фактора, так как здесь наблюдается высокое положительное факторное значение для факторной переменной fac1_1. В таком случае говорят, что существует отчётливая консистенция. По сравнению с предыдущим наблюдением, наблюдение 6 характеризуется очень высоким положительным значением факторной переменной fac2_1. Оно равно 1,23438. Исходя из значения фактора, можно сделать вывод, что существует сильное дружелюбное отношение к иностранцам. Соответственным образом ведут себя и отдельные значения элементарных переменных (a1 = 7, а2 = 7, а5 = 7, а8 = 7, а9 = 7, a11 = 7).

В заключение рассмотрим факторную переменную fac3_1. К ней относятся элементарные переменные аЗ, а6, а7 и а10. В качестве метки для этого фактора мы выбрали выражение: "Социальные страхи". Большое положительное значение фактора означает одобрение элементарных переменных. Одобрение элементарных переменных тождественно ярко выраженным социальным страхам. Рассмотрим для доказательства этого факта два примера. Наблюдение 5 характеризуется очень низким значением факторной переменной fac3_1. Оно равно —1,66369. В этом случае наблюдаются очень слабые социальные страхи и едва ли на основании социальных страхов можно наблюдать враждебное отношение к иностранцам. Соответственно этому ведут себя и отдельные значения элементарных переменных (аЗ = 5, аб = 2, а7 = 2, а 10 = 1). Наблюдение 43 в отличие от наблюдения 5 характеризуется очень высоким положительным факторным значением. Оно равно 1,93125. В этом случае наблюдаются очень сильные социальные страхи. Соответственным образом ведут себя и отдельные значения элементарных переменных (аЗ = 7, аб = 7, а7 = 7, а 10 = 7). В файле ausland.sav находятся ещё несколько дополнительных переменных, а именно:

ewv	Удовлетворённость собственным местом в экономических отношениях (1 = да, 2 = нет)
gebjg	Год рождения (1 = 1935-1949, 2 = 1941-1950, 3 = 1951-1960, 4 = 1961-1970)
geschl	Пол (1 = мужской, 2 = женский)
sozeng	Социально-политическая активность (1 = да, 2 = нет)
s+ellung	Занимаемая должность (1 = рабочий, 2 = специалист, 3 = служащий)

Эти переменные можно использовать для того, чтобы устанавливать связи для факторных значений. Самым распространённым методом для этого является разбиение факторных значений на четыре группы процентилей (см. гл. 8.6.2). Покажем это на примере первого факторного значения (переменная facl_l).

Выберите в меню Transform (Трансформировать) Rank Cases... (Создать иерархию наблюдений)

Откроется диалоговое окно Rank Cases (Создать иерархию наблюдений).

Переменную fac1_1 перенесите в список тестируемых переменных.

Щёлкните на выключателе Rank Types... (Типы иерархии), деактивируйте установленную по умолчанию опцию Rank (Ранг) и активируйте опцию Fractional rank as % (Дробный ранг как процентили). Оставьте установленное по умолчанию количество групп равное 4.

Подтвердите свой выбор нажатием на Continue (Далее) и затем на ОК.

Будет создана переменная nfac1_1, которая содержит значения 1 до 4 с примерно равномерной частотой.

Перейдите в редактор данных и измените имя переменной nfac1_1 на более удобное имя ausfeind, в поле метки наберите Враждебное отношение и значениям присвойте следующие метки: 1 = отсутствует, 2 = слабое, 3 = сильное и 4 = очень сильное. Теперь создадим таблицу сопряженности для новой переменной и переменной stellung (Занимаемая должность).

Выберите в меню Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Crosstabs... (Таблицы сопряженности)

В диалоговом окне Crosstabs (Таблицы сопряженности) переменную stellung поместите в поле строк, а переменную ausfeind в поле столбцов и через выключатель Cells... (Ячейки) сделайте дополнительно запрос на вывод процентных значений по строкам.

В окне просмотра появится следующая таблица сопряженности.

berufliche Stellung * fremdenfeindliche Einstellung Crosstabulation

(Занимаемая должность * Враждебное отношение Таблица сопряженности )
	fremdenfeindliche Einstellung (Враждебное отношение)	Total (Сум-ма)
keine (отсу-тствует)	swach (сла- бое)	stark (силь-ное)	sehr stark (очень силь- ное)
beru-fliche Ste- llung (Зани-маемая дол-жность)	Arbe- iter (Рабо-чий)	Count (Коли-чество)	6	7	7	11	31
% within berufliche Stellung (% от Зани-маемой долж-ности)	19,4%	22,6%	22,6%	35,5%	100,0%
Facha-rbeiter (Специ-алист)	Count (Коли-чество)	5	7	7	8	27
% within beru-fliche Stellung (% от Зани-маемой долж-ности)	18,5%	25,9%	25,9%	29,6%	100,0%
Anges-tellte (Служа-щий)	Count (Коли-чество)	10	9	8	3	30
% within beru-fliche Stellung (% от Зани-маемой долж-ности)	33,3%	30,0%	26,7%	10,0%	100,0%
Total (сумма)		Count (Коли-чество)	21	23	22	22	88
% within beru-fliche Stellung (% от Зани-маемой долж-ности)	23,9%	26,1%	25,0%	25,0%	100,0%

Враждебное отношение к иностранцам у рабочих и специалистов выражено ярче, чем у служащих. Однако тест по критерию Хи-квадрат демонстрирует о незначимом различии.

Попытайтесь найти связи между другими факторными значениями и переменными.

Диалоговое окно Factor Analysis:Options (Факторный анализ: Опции)

Total Variance Explained

(Объяснённая совокупная дисперсия)
Component (Компо-ненты)	initial eigenvalues (Первичные собственные значения)	Kotation Sums of Squared Loadings (Повёрнутая сумма квадратов нагрузок)
Total (Сумма)	% of Variance (% дис-персии)	Cumulative % (Совокупный процент)	Total (Сумма)	% of Variance (% дис-персии)	Cumulative % (Совокупный процент)
1	5,0226	14,359	14,359	4,388	12,538	12,538
2	3,937	11,250	25,609	3,972	11,349	23,887
3	2,356	6,731	32,340	2,396	6,845	30,732
4	2,073	5924	38,264	2,257	6,447	37,179
5	1,706	4,873	43,138	2,085	5,958	43,138
6	1,478	4,222	47,359
7	1,319	3,768	51, 127
8	1,258	3,595	54, 722
9	1,228	3,508	58, 230
10	1,082	3,092	61,322
11	1,029	2,941	64,263
12	,942	2,692	66. 955
13	,890	2,542	69, 497
14	,878	2,508	72, 005
15	,823	2,353	74, 358
16	,737	2,104	76, 462
17	,704	2,011	78, 473
18	,664	1,898	80, 371
19	,652	1,862	82, 232
20	,618	1,766	83, 998
21	,572	1,634	85, 632
22	,516	1,474	87, 106
23	,473	1,352	88, 458
24	,466	1,331	89, 788
25	,459	1,310	91,099
26	,432	1,234	92, 332
27	,417	1,192	93, 524
28	,388	1,108	94, 632
29	,345	,985	95,617
30	,324	,927	96, 544
31	,287	,821	97, 365
32	,259	,740	98, 105
33	,240	,684	98, 789
34	,223	,638	99, 427
35	,201	,573	100,000

Extraction Method: Principal Component Analysis (Метод отбора: Анализ главных компонентов).

Насчитывается одиннадцать собственных значений, превосходящих единицу, что означало бы отбор одиннадцати факторов, если бы Вы не изменили установку по умолчанию Eigenvalues over: 1 (Собственные значения, превосходящие единицу) и не ограничили бы количество рассматриваемых факторов пятью. После точечной диаграммы, которую мы объясним позже, следует вывод повёрнутой факторной матрицы:

Rotated Component Matrix a

(Повёрнутая матрица компонентов)
	Component (Компоненты)
1	2	3	4	5
F5	,683
F16	,683
F22	,620
F9	,581
F26	,580
F6	,544
F35	,515
F33	,491
F12	,488
F34	,458
F4	,447
F7		,710
F8		,690
F17		,654
F14		,621
F15		,597
F18		,589
F19		,572
F1		,563
F13		,510
F20
F28			,816
F27			,765
F31			-,493
F29
F21				,683
F25				,592
F30				,522
F23	,426			,469
F24				,404
F3					,677
F2	,457				,567
F10					-,564
F11					,403
F32

Extraction Method: Principal Component Analysis (Метод отбора: Анализ главных компонентов).

Rotation Method: Varimax with Kaiser Normalization (Метод вращения: варимакс с нормализацией Кайзера).

a. Rotation converged in 6 iterations (Вращение получено за б итераций).

Здесь мы опять подходим к самой интересной части факторного анализа — толкованию факторов. Факторные нагрузки пяти факторов в блочном виде расположены по диагонали матрицы. Переменные, находящиеся внутри одного блока, отсортированы в порядке убывания факторных нагрузок, причём был запрещен вывод факторных нагрузок, меньших 0,4. Высказывания f5, f16, f22, f9, f26, f6, f35, f33, f12, f34 и f4 принадлежат первому фактору, высказывания f7, f8, f17, f14, f15, f18, f19, f1, f1З и f10 второму и т.д. Высказывание f5 своим значением 0,683 нагружает сильнее всего первый фактор, высказывание f7 — второй фактор (со значением 0,710), высказывание f28 — третий фактор (со значением 0,816) и т.д.

Для того, чтобы отдельные высказывания отнести к определенному фактору, при выводе отсортированных значений Вам уже не нужно маркировать их карандашом, так как сопоставление в этом случае будет произведено автоматически. Несмотря на то, что представление данных в таком виде значительно удобнее, всё же здесь существует один серьёзный недостаток: сопоставление высказывания некоторому фактору рассматривается как единственно верное решение, без проверки, не имеет ли данное высказывание примерно такую же нагрузку и для какого-либо другого фактора. Рассмотрим, к примеру, пунктf23. Пункт f23 нагружает фактор 1 значением 0,426, а фактор 4 значением 0,469. Для обеспечения корректности в этом случае следует иметь дело с обоими факторами. Если нельзя чётко объяснить принадлежность одного из многих высказываний одному-единственному фактору, то факторный анализ следует считать неудавшимся. Аналогично, Вы не должны забывать об этой проблеме при выводе сортированных данных. Кроме того, факторный анализ считается неудавшимся и тогда, когда нельзя однозначно интерпретировать факторы. Поэтому далее мы попытаемся интерпретировать факторы из рассматриваемого примера.

Фактор 1:

Винить самого себя

Жалеть себя

Впасть в бесконечные размышления

С нетерпением и раздражённо на всё реагировать

Жаловаться на судьбу

Считать виноватыми других

Пытаться припомнить личный опыт и методы борьбы с подобными ударами судьбы

Искать улучшение настроения в употреблении алкоголя или успокаивающих средств

Размышлять и мечтать о своём

Фактор 2:

Предпринимать активные действия для решения проблемы

Составить план и затем приступить к действиям

Подбадривать себя

Пытаться интенсивней жить

Решиться на борьбу с болезнью

Пытаться достичь успеха и самоутверждения

Пытаться отвлечься

Искать информацию о заболевании и лечении

Фактор 3:

Надеяться на врачей

Точно следовать указаниям врача

Изображать наигранное веселье

Фактор 4:

Принимать болезнь как судьбу

Утешать себя тем, что другим ещё хуже

Желать делать добро другим

Искать утешения в религии

Пытаться найти какой-либо смысл в болезни

Фактор 5:

Занижать значение и важность болезни Не желать признать случившееся Выносить все эмоции наружу Подавлять эмоции, самообладание

В этом примере, также как и в предыдущем случае, можно без особых усилий истолковать содержание этих факторов.

Первый фактор собрал все пункты, описывающие депрессивное отношение к тяжёлой болезни. Эти пункты описывают состояние подавленности, удручённости и сомнений; здесь речь идёт о потере желания жить и попытке спрятаться за алкоголем и психотропными средствами. Обозначим фактор 1 меткой "Депрессивный подход".

Второй фактор собрал все пункты, описывающие активный подход к борьбе с болезнью. Эти пункты описывают состояние пробуждения желания жить, которое проявляется в рациональном подходе к борьбе с болезнью (Поиск информации), в нежелании позволить болезни ввести себя в угнетённое состояние (Пытаться отвлечься). Фактору 2 присвоим следующую метку: "Активное действие, направленное на решение проблемы".

Третий фактор собрал все пункты, основывающиеся на отношении врач-пациент. Следует обратить внимание на то, что высказывание f31 отрицательно нагружает этот фактор, то есть о наигранном веселье скорее всего речь не идёт. Для краткой характеристики этого фактора можно было бы выбрать выражение: "Надеяться на врачей".

Фактор 4 собрал все высказывания, указывающие на фаталистический или религиозно-направленный поиск смысла происходящего. В качестве краткой характеристики здесь можно было бы выбрать выражение: "Религиозность и поиск смысла".

В факторе 5 собрались все пункты, характеризующие состояние, в котором опрашиваемый не склонен признавать болезнь путём занижения её важности или нежелания осознавать реальность, а также душевной отчуждённости (Подавлять эмоции). Здесь следует обратить внимание на то, что пункт f10 (Выносить все эмоции наружу) нагружает фактор отрицательным значением, то есть эмоции скорее не выносятся наружу. В качестве краткой характеристики этого фактора можно было бы выбрать выражение: "Недооценка и психологическая отрешённость".

Точечная диаграмма

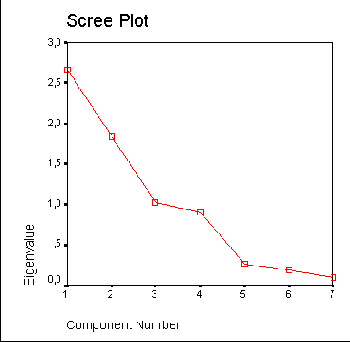
Займёмся теперь анализом точечной диаграммы, представленной на рисунке 19.7.

Точечная диаграмма может нам помочь определить количество учитываемых факторов. Как Вам уже известно, согласно установке по умолчанию, SPSS учитывает в результирующей модели все те факторы, собственное значение которых превосходит единицу. В нашем примере это было бы одиннадцать факторов.

Количество учитываемых факторов вы можете задать сами, что мы и сделали ранее. В качестве вспомогательного средства для определения задаваемого числа факторов может послужить специальная точечная диаграмма. Слово Screeplot, употребляемое для обозначения этой диаграммы состоит из двух частей: английского слова scree, что означает щебень и слова plot, что в английском соответствует графическому представлению. Такая диаграмма служит для того, чтобы маловажные факторы — щебень — можно было отделить от самых значимых факторов. Эти значимые факторы на графике образовывают в своего рода склон, то есть ту часть линии, которая характеризуется крутым подъёмом. В приведенной диаграмме такой крутой подъём наблюдается

в области первых пяти факторов. Пять факторов мы и положили в основу модели в самом начале анализа. Если посмотреть на график, то можно заметить что склон, то есть область значимых факторов, наблюдается выше пятого фактора (пятый, четвёртый, третий, второй ...), а ниже пятого фактора (шестой, седьмой, восьмой ...) расположился щебень, область незначимых факторов. Вы можете самостоятельно провести расчет с использованием модели, включающей различное число факторов; в рассмотренном примере было бы уместным произвести сравнение моделей с учётом четырёх, пяти и шести факторов.

Диалоговое окно Factor Analysis:Rotation (Факторный анализ: Вращение)

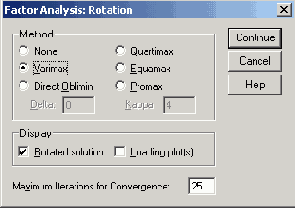
В заключение, с помощью кнопки Options... (Опции) Вы получите возможность, организовать вывод коэффициентов, отсортированных по размеру. В отличие от первого примера факторного анализа, здесь мы воспользуемся предлагаемой сортировкой.

Поэтому активируйте опцию Sorted by size (Сортированные по размеру).

Факторный анализ

Факторный анализ это процедура, с помощью которой большое число переменных, относящихся к имеющимся наблюдениям сводит к меньшему количеству независимых влияющих величин, называемых факторами. При этом в один фактор объединяются переменные, сильно коррелирующие между собой. Переменные из разных факторов слабо коррелируют между собой. Таким образом, целью факторного анализа является нахождение таких комплексных факторов, которые как можно более полно объясняют наблюдаемые связи между переменными, имеющимися в наличии.

Факторный анализ

Глава 19. Факторный анализ

Факторный анализ 19.1 Порядок выполнения факторного анализа 19.2 Пример из области социологии 19.3 Пример из области психологии 19.4 Задача вращения

Компонентная диаграмма без вращения

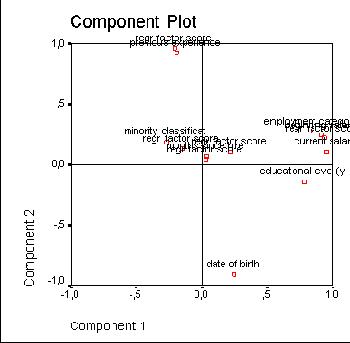
На этой диаграмме в графическом виде представлены факторные нагрузки обоих факторов. Для интерпретации факторов было бы оптимально, если бы точки лежали ближе к осям и подальше от точки начала отсчёта; тогда каждая переменная имела бы значительную нагрузку для одного фактора и незначительную для другого. Этого можно достичь поворотом осей против часовой стрелки, причём ортогональность системы координат (прямой угол между осями) должна сохраниться. В данном двумерном примере это вращение можно представить себе довольно наглядно, математически же подобный поворот можно произвести также и в и—мерном пространстве (то есть при наличии произвольного количества факторов).

Альтернативой прямоугольному (ортогональному) вращению является косоугольное вращение. В этом случае после вращения оси не сохраняют прямой угол по отношению друг к другу. В то время как при прямоугольном вращении корреляция между факторами отсутствует, то при косоугольном вращении этот принцип нарушается — факторы могут коррелировать между собой.

SPSS предлагает в общей сложности пять методов вращения: три метода для ортогонального вращения, один для косоугольного и еще один, который является комбинацией двух видов вращения. Эти методы Вы можете активировать через выключатель Rotation... (Вращение) в диалоговом окне Factor Analysis: Rotation (Факторный анализ: Вращение).

Varimax: Ортогональное вращение, при котором происходит минимизация количества переменных с высокой факторной нагрузкой. Этот метод является наиболее часто применяемым, поскольку он облегчает интерпретацию факторов.

Quartimax: Ортогональное вращение, при котором происходит минимизация количества факторов, необходимых для объяснения переменной. Этот метод используется редко и вообще не рекомендуется для применения.

Equamax: Ортогональное вращение; компромисс между предыдущими методами.

Direct oblimin: Косоугольное вращение.

Рrоmах: Комбинация ортогонального и косоугольного видов вращений.

Обычно для ортогонального вращения применяют метод варимакса, а для косоугольного — Direct oblimin. При помощи компонентной диаграммы отследим действие вращения, осуществленного с использованием метода варимакса.

В диалоговом окне Factor Analysis: Rotation (Факторный анализ: Вращение) вместо опции None (Отсутствует) активируйте опцию Varimax (Ba-римакс).

Рассмотрите изменённую компонентную диаграмму.

Компонентная диаграмма после вращения

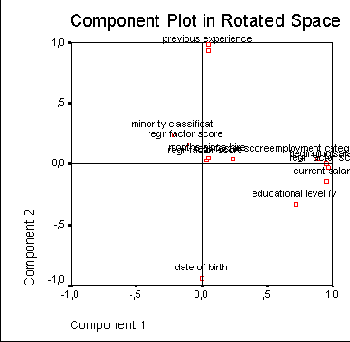
На диаграмме стало заметно смещение факторных нагрузок в сторону главных осей.

Факторный анализ является самым излюбленным приёмом практических статистиков, служащим для сокращения количества переменных. Наиболее интересной частью факторного анализа является толкование получающихся факторов, над которым, правда, придётся поразмыслить и применить весь имеющийся опыт.