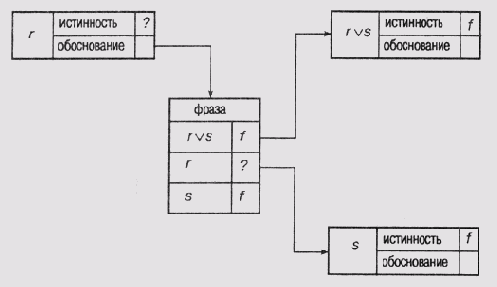
Отслеживание зависимостей
В главе 15 рассказывалось о том, что в экспертной системе VT для фиксации зависимостей между решениями, принимаемыми в процессе проектирования, используется сеть зависимостей. В такой сети узлы соответствуют присвоению значений конструктивным параметрам, причем между узлами существуют два вида связей— связи содействия (contributes-to) и связи принуждения (constrains). Узел А содействует узлу В, если значение параметра А появляется в результате вычисления значения В, а узел А принуждает узел В, если значение параметра A запрещает параметру В принимать определенные значения. В дальнейшем для некоторой формализации изложения будем обозначать узлы прописными буквами, а строчными— значения соответствующих параметров. Например, значение, присваиваемое узлу (параметру) А в какой-либо момент времени, будем обозначать как а.
Релаксация в сети
Основное назначение связей в сети зависимостей состоит в том, чтобы, во-первых, показать, как изменение значения какого-либо параметра распространяется от узла к узлу, а во-вторых, выявить противоречия между значениями, присвоенными разным узлам.
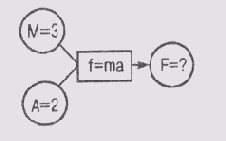
Пусть, например, в сети имеются узлы А и М. Узел А представляет ускорение некоторой детали механизма, а М— массу этой детали. Оба узла, А и М, содействуют узлу F, который представляет силу, действующую на деталь. Более того, учитывая знакомую всем со школьной скамьи формулу f= та, узлы А и М также и принуждают узел F, поскольку если а и т известны, то значение f определяется этой формулой и не может быть произвольным, т.е. если а - 2 и от = 3, то мы можем присвоить узлу F только значение f= 6. Если же этому узлу уже ранее было присвоено значение f= 7, то сеть переходит в состояние противоречия.
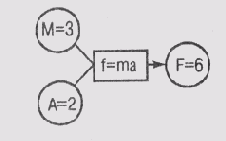
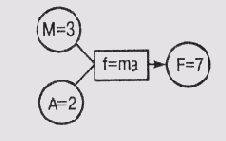
Формула f= та играет роль принудительного ограничения для сети, описанной в этом примере. Если все ограничения в сети удовлетворяются, то она пребывает в состоянии релаксации. Рассмотрим варианты сетей, представленные на рис. 19.1. Сеть а) находится в промежуточном состоянии, поскольку узлу F не присвоено какого-либо определенного значения, сеть б) находится в состоянии релаксации, а сеть в) — в состоянии противоречия.
Строго говоря, термин "релаксация" относится к сети, а не к теории13. Но сеть есть не что иное, как только представление определенной теории, например сеть а) является представлением теории
f= mа т=3
а = 2,
в которой формула f= та играет роль принудительного ограничения. Сеть б) представляет теорию
f= mа т=3
а = 2 f=6,
которая находится в состоянии релаксации по отношению к ограничению f= та, а сеть в) представляет противоречивую теорию
f= mа
т=-3
а = 2 f=7.
По ходу изложения, не оговаривая отдельно, мы будем "перескакивать" от сетей к теориям, а для простоты использовать термин "представление", если нежелательно подчеркивать различие между этими двумя способами-реализации фактов и ограничений.
а
б
с
Рис. 19.1. Сети зависимостей с принудительными ограничениями. Окружностями представлены узлы сети, а прямоугольниками — связи
Пересмотр допущений
Практически во всех программах экспертных систем в процессе решения проблемы обязательно тем или иным образом обновляются представления реального мира вещей, с которыми эта программа имеет дело (например, так происходит в программе планирования поведения роботов STRIPS, которую мы рассматривали в главе 3). В программах с разным уровнем "интеллектуальности" для пересмотра допущений в этом представлении применяются более или менее сложные методы. В литературе можно найти такую классификацию этих методов.
(1) Монотонный пересмотр (monotonic revision). Это самый простой метод, при котором программа принимает информацию о новых фактах и вычисляет, как эти факты могут повлиять на имеющееся представление, чтобы оно перешло в результате в состояние релаксации. При этом предполагается учитывать "важные" последствия, хотя определить, какие последствия важные, а какие не очень, зависит от уровня интеллектуальности программы. Например, к важным скорее будет отнесен вывод q из р и (р

(2) Немонотонный пересмотр (nonmonotonic revision). Иногда бывает желательно "взять назад" принятые ранее допущения и урезать сделанные на их основе заключения. Если я вижу вас за рулем "Мерседеса", то первое предположение — что он ваш собственный, а следовательно, вы, мягко говоря, человек не бедный. Но если через некоторое время я узнаю, что вы его, пользуясь терминологией Гека Финна, "позаимствовали", то я должен буду отбросить не только предположение, что он ваш собственный, но и предположение о вашем богатстве.
(3) Немонотонное обоснование (nonmonotonic justification). Дальнейшее усложнение метода происходит в тех программах, в которых определенные предположения полагаются истинными в том случае, когда нет никаких явных свидетельств против такого предположения. Например, программа может предполагать, что все студенты малообеспечены. Отказ от такого предположения в отношении определенного студента выполняется в программе только в том случае, если на лицо явные признаки более чем среднего материального благополучия. Здесь именно отсутствие информации, противоречащей первоначальному допущению, а не наличие подтверждающей информации является обоснованием его правдоподобия.
(4) Гипотетическое суждение (hypothetical reasoning). В программе можно сначала принять во внимание определенные предположения, а затем посмотреть, что из них следует. Далее из этих предположений можно отобрать правдоподобные допущения. Таким образом, в этом способе предполагается формировать рассуждения в разных мирах, т.е. в таких состояниях представления о реальной области знаний, которые могут соответствовать или не соответствовать реальности. Отслеживание множества теорий такого вида требует определенных дополнительных ресурсов по сравнению с методами, предполагающими исследование единственной теории.
Методы первой из перечисленных категорий довольно тривиальны: нужно добавить в имеющуюся теорию новую информацию и некоторые дополнительные факты, которые необходимы, чтобы перевести новую теорию в состояние релаксации по отношению к имеющимся ограничениям. Простой метод, демонстрирующий реализацию второй из перечисленных категорий, мы рассмотрим в следующем разделе, а в разделах 19.3 и 19.4 рассмотрим методы третьей и четвертой категорий.
19.1.
Запись информации о связях
;; ШАБЛОНЫ
;; Литерал - атомарное высказывание, (deftemplate literal (field id (type INTEGER))
(field atom (type SYMBOL))
(multifield support (type INTEGER) (default -1))
| )
Условие является импликацией в форме
;; "Р имплицирует Q", где "P" является левой частью правила
;; (left-hand side = Ihs), ;; "Q" - правой частью
;; (right-hand side = rhs).
(deftemplate conditional
(field Id (type INTEGER))
(multifield Ihs (type SYMBOL))
(multifield rhs (type SYMBOL)) )
;; Нам понадобится индекс в рабочей памяти, чтобы ;; можно было присваивать идентификаторы новым ;; производным высказываниям, (deftemplate index
(field no (type INTEGER)) )
;; Исходная модель мира. (deffacts model
(conditional (id 0) (Ihs P) (rhs Q);
(literal (id 1) (atom P)) )
;; ПРАВИЛА
;; Присвоить значение индекса очередному идентификатору, (defrule init
?F <- (initial-fact)
(literal (id ?N))
(not (literal (id ?M&:{> ?M ?N)))) =>
(assert (index (no (+ ?N 1))))
(retract ?F) )
;; Применить правило modus ponens, чтобы можно было ;; вывести "Q" из "Р" и "Р имплицирует Q", формируя ;; указатели на "Р" и "Р имплицирует Q" в попе ;; support литерала "Q". (defrule mp ?I <- (index (no ?N)) (conditional (id ?C) (Ihs $?X) (rhs $?Y)) (literal (id ?A) (atom $?X)) (not (literal (atom $?Y)))
(assert (literal (id ?N) (atom $?Y) (support ?C ?A))) (modify ?I (no (+ ?N 1)))
Эта примитивная программа имеет дело только с условными выражениями и атомами. Например, нельзя, используя правило modus fallens (см. главу 8), вывести "не Р" из "Р имплицирует Q" и "не Q".
Пересмотр теорий высказываний
Систему отслеживания истинности предположений, разработанную Мак-Аллестером [McAllester, 1980], нельзя отнести к самым первым, но ее, пожалуй, лучше всего использовать в качестве наглядного пособия. Использованный им метод пересмотра предполагает наличие в системе базы данных утверждений, в которой пользователь может квалифицировать формулы как "истинные", "ложные" или "неопределенные". Таким образом, в основе метода лежит трехзначная логика, в отличие от классической двузначной, которую мы рассматривали в главе 8. Система представляет утверждения в виде узлов, которые хранят соответствующие значения.
Ограничения, которые накладывает на содержимое базы данных утверждений система отслеживания истинности, представляют собой фундаментальные аксиомы логики высказываний. Например, аксиома ¬(U^¬U)
утверждает, что высказывание U может быть одновременно и истинным, и ложным. (Учтите, что -U является метапеременной, которая представляет любое высказывание.) Система отслеживания истинности предположений, разработанная Мак-Аллестером, как и большинство других подобных систем, имеет дело только с формулами, которые не содержат кванторов. Например, в теорию может входить высказывание DEAD(fred), но не может входить (любой X)(DEAD(X)). Это ограничение существует по той простой причине, что не всегда возможно установить совместимость теории первого порядка, как это отмечалось в главе 8.
Система отслеживания истинности выполняет по отношению к базе данных четыре функции.
(1) Реализует множество дедукций высказываний, которые Мак-Аллестер назвал распространением пропозициональных принуждений (propositional constraint propagation).
(2) Формирует обоснования при присвоении высказываниям значений истинности, когда такое присвоение выполняется в результате распространения принуждений (а не при установке значения пользователем). Таким образом, если мы приходим к заключению, что q истинно, поскольку истинны p и (p

(3) Обновляет базу данных утверждений, как только какое-либо высказывание удаляется. Так, если мы приходим к выводу, что q истинно, поскольку истинны р и (p

(4) Отслеживает цепочку предположений, которые привели к противоречию, с помощью метода, получившего наименование обратное прослеживание, ведомое зависимостями (dependency-directed backtracking). После этого пользователю предлагается удалить одно из предположений, "виновных" в появлении противоречия.
Задавшись предположениями р и (— p v q) и пользуясь механизмом распространения принуждений, система отслеживания истинности может получить q. Затем она формирует поддерживающую структуру, представленную на рис. 19.2. Каждый узел в этой сети представляет собой фрейм (см. о фреймах в главе 6) с набором слотов, один из которых хранит наименование узла, другой — значение истинности, а третий — указатель на обоснование. Обоснование представлено другим фреймом, который содержит таблицу поддерживающих высказываний и их значения истинности. В структуре на рис. 19.2 истинность узла q подтверждается тем фактом, что узлы, представляющие р и (— p v g), отмечены как имеющие значения "истина". Обратите внимание на то, что узлы, представляющие предположения, как, например, р, не имеют указателей на фреймы обоснования, поскольку они полагаются истинными по определению.
Если в дальнейшем окажется, что значение q несовместимо с содержимым остальной базы данных утверждений, то, анализируя описанную структуру данных, можно будет выйти на фреймы обоснования. После этого пользователю будет предоставлена возможность проследить цепочку зависимостей, связанную либо с р, либо с (-p v q). Для выполнения такого отслеживания очень важно, чтобы структуры поддержки были убедительными. Убедительность структуры означает отсутствие зацикливания, т.е. отсутствие такой ситуации, когда некоторое высказывание не подтверждает через "посредников" само себя.
Обратите внимание — все утверждения являются либо предположениями, введенными пользователем, либо обосновываются наличием других утверждений. В следующем разделе мы рассмотрим другую, более сложную систему отслеживания истинности предположений, в которой допускается использовать в качестве обоснования отсутствие запрещающей информации.
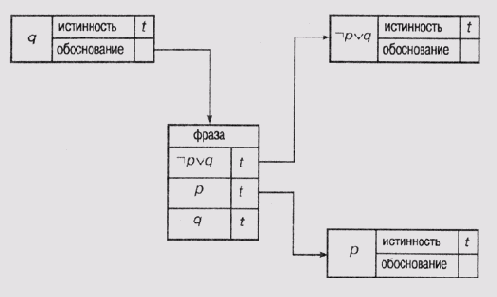
Рис. 19.2. Структура представления связей между высказываниями
Немонотонное обоснование
Подход, предложенный Дойлом [Doyle, 1979], отличается от того, который применил Мак-Аллестер. Он основан на философии "здравого смысла", в частности на презумпции значения по умолчанию. В первом приближении, помимо хранения допущений, подтвержденных какими-либо свидетельствами, хранятся также допущения, основанные на резонном предположении, т.е. допущения, свидетельства против которых отсутствуют.
Обоснования (или, пользуясь терминологией Доила, резоны) в пользу допущения Р представляют собой упорядоченную пару списков (INP, OUTp ). Список INp— обычные обоснования в форме, которая аналогична использованной Мак-Аллестером. Он содержит высказывания, истинность которых является необходимым условием истинности Р. Список OUTp содержит высказывания, присутствие которых во множестве допущений указывает на ложность Р. Это множество получило название множества немонотонных обоснований (nonmonotonic justification), поскольку добавление высказывания в него потребует отказаться от сделанного ранее допущения. В подходе, который рассматривался Мак-Аллестером, этот вариант не анализировался.
Пусть, например, обоснование для значения р имеет вид
({}, {-p}).
Это означает, что можно предполагать наличие р до тех пор, пока это обоснование не станет ложным. Обоснование для q пусть имеет вид
({p}, {r}).
Такое обоснование означает, что можно предполагать наличие q до тех пор, пока высказывание р присутствует в множестве текущих допущений (в терминологии Доила — получает статус поддержки (support status) "включено" — in), а высказывание r отсутствует в множестве допущений (в терминологии Доила — получает статус поддержки "исключено" — out). Обратите внимание на то, что обоснования могут быть связанными, как в приведенном выше примере. Если -р имеет статус исключено, то, следовательно, р имеет статус включено, а тогда и q имеет статус включено до тех пор, пока r имеет статус исключено.
Такая цепочка причинно-следственных связей называется SL-обоснованием (SL — сокращение от support list). Общее правило для SL-обоснований гласит, что допущение Р присутствует в текущем множестве допущений только в том случае, если каждое из допущений, перечисленных в списке IN, имеет статус включено, а каждое из допущений, перечисленных в списке OUT, имеет статус исключено.
Дуальная структура обоснований, предложенная Дойлом, может быть использована для разделения допущений на три группы.
(1) Посылки (premises), т.е. высказывания, которые полагаются истинными без всякого обоснования (по определению). Пользуясь обозначениями из теории множеств, можно следующим образом представить определение посылки:
{Р
 p= OUTp = не существует } .
p= OUTp = не существует } .(2) Дедукции (deductions), т.е. высказывания, которые являются заключениями нормальной монотонной дедукции. В обозначениях теории множеств дедукции представляются выражением
(2) Проверить консеквенсы данного узла. Если таковых не существует, то изменить статус узла с исключено на включено, сформировать связанные с ним списки IN и OUT и на этом закончить. В противном случае сформировать список L, в который включить узел и его множество последствий, зафиксировать статус включено-исключено каждого из этих узлов, временно присвоить им статус nil и перейти к шагу (3).
(3) Для каждого узла N из списка L попытаться отыскать действительное и убедительное обоснование, которое позволяет изменить статус этого узла на включено. Если таковое найдено не будет, присвоить узлу статус исключено. В любом варианте изменения статуса узла распространить это изменение на его консеквенсы. (Примечание. Обоснование является действительным, если каждый узел, перечисленный в его списке IN, имеет статус включено, а каждый узел, перечисленный в списке OUT, — статус исключено. Обоснование является убедительным в том случае, когда в его логической цепочке отсутствует зацикливание. Например, обоснования ({-Р},{}) и ({},{Р}) являются зацикленными по отношению к Р. Из первого следует, что Р имеет статус включено только в случае, если —P также имеет статус включено, а из второго следует, что Р имеет статус включено только в случае, если Р имеет статус исключено. Таким образом, каждое обоснование, если применить его в отношении высказывания Р, приводит к противоречию.)
(4) Если некоторый узел в списке L имеет состояние включено и отмечен как противоречивый, то запустить процедуру обратного прослеживания, ведомого зависимостями (dependency-directed backtracking). Если в процессе выполнения этой процедуры вновь возникнут условия для запуска процесса отслеживания истинности предположений (шаги (1)-(3)), повторять эти шаги до тех пор, пока не будут разрешены все противоречия.
(5) Сравнить текущий статус поддержки каждого узла из списка L с его прежним статусом, зафиксированным ранее, и известить пользователя обо всех произведенных изменениях статуса.
Обе системы — и Мак-Аллестера, и Доила — демонстрируют более "интеллектуальный" подход к решению проблемы адекватного и непротиворечивого описания мира, чем тот, который был использован в рассмотренной ранее системе STRIPS (см. главу 7). В обоих случаях системы отслеживания истинности предположений берут на себя заботы об обновлении модели мира посредством распространения аналогов операций ADD и DELETE по сети зависимостей. Если при этом обнаруживается, что в модели возникли противоречия, пользователю предлагается отказаться от какой-либо из посылок, которые послужили причиной такого противоречия, и восстановить тем самым целостность модели.
19.2.
Пара конфликтующих выражений
;; ШАБЛОНЫ
;; Литерал - атомарное высказывание.
(deftemplate literal (field id (type INTEGER}) (field atom (type SYMBOL)) (field status (type SYMBOL) (default unk)) (multifield inlist (type INTEGER) (default -1)) (multifield outlist (type INTEGER) (default -1))
)
;; Исходная модель мира.
(deffacts model
(literal (id 0) (atom P) (status in) (outlist 1) ) (literal (id 1) (atom Q) (status in) (outlist 0) )
)
;; ПРАВИЛА
;; Если выражение в списке outlist
;; выражения S имеет статус out
;; и выражение S имеет пустой список inlist,
;; то присвоить выражению S статус in.
(defrule in
(literal (id ?A) (status out)) ?F <- (literal (status out) (inlist -1) (outlist ?A))
=> (modify ?F (status in))
)
Если выражение в списке outlist выражения S имеет статус in, то присвоить выражению S статус out. Обратите внимание на то, что в этом правиле наличие списка inlist для выражения S не имеет значения, (defrule out
(literal (id ?A) (status in)) ?F <- (literal (status in) (outlist ?A)) =>
(modify ?F (status out)) )
;; Это правило предлагает пользователю удалить ;; выражение и таким образом уладить конфликт, (defrule deny
(declare (salience -10))
?L <- (literal (atom ?X) (status in) (inlist -1)) =>
(printout t crlf "Deny " ?X "? ")
(bind ?ans (read)) (if (eq Pans yes) then (modify PL (status out)))
;; Что произойдет после того, как вы ;;запустите эту программу на выполнение? ;;Как ! будет вести себя программа, если ;;в ответ на запрос, сформированный правилом ;; deny, ввести yes? Как будет ;;вести себя программа, получив ответ по?
Работа со множеством контекстов
Те системы отслеживания истинности предположений, которые мы рассматривали в предыдущих разделах, работали с единственной непротиворечивой моделью мира. Однако иногда возникает необходимость строить логический вывод в контексте разных моделей гипотетических миров, которые могут совпадать, а могут и не совпадать с реальностью (см. главу 17). Например, при решении задачи диагностирования часто бывает полезно предположить, что возникла какая-то ошибка, и выдвинуть предположение на основе какого-нибудь допущения, а затем посмотреть, не подтверждается ли оно имеющимися фактами. Особенно уместна такая стратегия в ситуации, когда результаты наблюдений дают пищу для множества конкурирующих гипотез и скорее всего потребуется какая-либо комбинация гипотез, чтобы объяснить всю совокупность наблюдений. Другая область применения, в которой потребуется рассмотреть несколько вариантов модели мира, — проектирование. Вот тут-то уж точно потребуется несколько гипотетических "миров", чтобы представить разные варианты конструкции, удовлетворяющей заданным ограничениям.
Отслеживание истинности предположений, основанное на анализе допущений
В системах отслеживания истинности предположений, основанных на анализе допущений {assumption-based truth-maintenance system), программа имеет дело с несколькими отличающимися контекстами, которые принято называть средами обитания (environments) [De Kleer, 1986]. Удобнее всего представить себе среду обитания как взгляд на мир через призму определенных допущений. Можно считать, что модель мира, которая использовалась в предыдущих разделах, характеризуется пустым множеством допущений. Все прочие среды, имеющие непустое множество допущений, представляют модели гипотетических миров.
В системах отслеживания истинности предположений, основанных на допущениях, различные варианты сред обитания можно организовать в виде решетки, поскольку допущения носят инкрементальный характер. Модель, показанная на рис. 19.3, представляет на самом нижнем уровне автомобиль, в котором не горит свет и который не удается завести. На более верхнем уровне решетки находятся гипотетические миры, в которых сделаны некоторые допущения о неисправностях в автомобиле, например разряжена аккумуляторная батарея. На еще более высоком уровне можно комбинировать сделанные допущения. Обратите внимание — чем выше мы поднимаемся "по ступеням решетки", тем более специфическими становятся гипотетические миры в том смысле, что мы характеризуем их все полнее.
Не всегда можно делать произвольные допущения. Например, нельзя объединить допущения {p,q} и {—p,r}, поскольку такая комбинация будет противоречивой. Более того, хотя само множество допущений может и не быть антагонистическим, определенные комбинации допущений могут привести к противоречию, если принять во внимание и другую имеющуюся в нашем распоряжении информацию.
Предположим, что наша модель неисправного автомобиля содержит информацию о том, что одновременно не может случиться так, чтобы и карбюратор не работал из-за избытка топлива, и в баке отсутствовал бензин. Следовательно, в том варианте среды, в котором сделано допущение "в баке отсутствует бензин", не может присутствовать допущение "избыток топлива в карбюраторе". Такое логическое заключение образует контекст среды — множество высказываний, производных от сделанных допущений, и фактов, имеющихся в исходной модели мира. Например, мы можем оказаться в ситуации, представленной схематически на рис. 19.4. Здесь среда, образованная в результате объединения двух допущений, должна быть исключена из рассмотрения, поскольку ее контекст становится несовместимым (nogood).

Рис. 19.3.
Решетка сред
В системах отслеживания истинности предположений, основанных на анализе допущений, такие зависимости называются обоснованиями (justification). Конечно, такая вольная трактовка термина "обоснование" вносит некоторую неоднозначность в изложение материала (ранее мы придавали этому термину несколько другой смысл), но дело в том, что обоснование в тех системах, которые рассматриваются в данном разделе, играет роль, отличную от обоснований в простых системах отслеживания истинности, анализированных Мак-Аллестером и Дойлом. В тех системах обоснования формировались программой в результате распространения принуждений и связывались с узлами сети зависимостей, которые представляли высказывания.

Рис. 19.4.
Решетка сред, в которой выделен несовместный контекст
На рис. 19.4 отрицание высказывания "Нет бензина в баке" существует в среде, в которой сделано допущение "Избыток топлива в карбюраторе", причем в модели имеется обоснование, которое гласит примерно следующее:
"Если в карбюраторе имеется избыток топлива, то бензин не может отсутствовать в баке".
Теперь интересующее нас высказывание будет "по наследству" истинно и в несовместимом контексте, но такая среда не представляет интереса для этого высказывания и, следовательно, в список ярлыка не включается.
Предположим также, что в модели имеется обоснование
"Если свечи влажные, то бензин не может отсутствовать в баке".
В этом случае отрицание высказывания "Нет бензина в баке" имеет место в среде, в которой сделано допущение "Влажные свечи", как показано на рис. 19.5. Эту среду уже имеет смысл включить в список ярлыка. Теперь ярлык интересующего нас высказывания будет содержать список, в котором перечислены два варианты среды, причем каждый из вариантов не содержит противоречий. На рисунке эти варианты среды заштрихованы. Как и ранее, варианты, представляющие несовместимый контекст (на рисунке они выделены прямоугольниками с утолщенными линиями контура), мы будем игнорировать.

Рис. 19.5.
Решетка сред, в которой узлы, имеющие непустые списки ярлыков, заштрихованы
Таким образом, из всего сказанного выше вытекает, что основная забота системы отслеживания истинности предположений, основанной, на анализе допущений, состоит в формировании списка сред для узлов высказываний. Такой список может быть созвучным (sound), завершенным (complete), совместимым (consistent) или минимальным (minimal) ярлыком. В эти термины вкладывается следующий смысл.
Ярлык является созвучным, если высказывание, к которому он относится, является производным от каждой среды, включенной в этот ярлык, т.е. оно имеет статус включено в контексте каждой такой среды.
Ярлык является завершенным, если любая непротиворечивая среда, в которой имеет место соответствующее высказывание, либо присутствует в списке, либо образована включением дополнительных допущений в ту среду, которая присутствует в списке.
Ярлык является совместимым, если любая среда, включенная в список, является непротиворечивой.
Ярлык является минимальным, если ни одна среда, включенная в список, не образуется добавлением какого-либо допущения к той среде, которая также присутствует в списке.
Если узел высказывания в сети имеет пустой ярлык, это означает, что высказывание не является производным ни от какого совместимого множества допущений. Другими словами, это высказывание не может быть истинным ни при каких совместимых комбинациях допущений. Например, ярлык узла, соответствующего высказыванию "отсутствует бензин в баке и влажные свечи", будет иметь пустой список.
Использование систем отслеживания истинности предположений для диагностирования
на основе моделей
Выше, в главах
11 и 12, были рассмотрены экспертные диагностические системы, в которых использовался
метод эвристической классификации. Этот метод предполагает, что большая часть
знаний представлена в виде эвристических правил, связывающих абстрактные категории
данных (типичные симптомы) с абстрактными категориями решений (типичные неисправности).
Такая форма представления знаний иногда называется "поверхностной",
поскольку знания не содержат информации о причинных связях между симптомами
и неисправностями (теорию функционирования диагностируемого объекта — машины
или живого организма), а отражают только эмпирический опыт. Информация о причинно-следственных
связях, определяющих поведение и свойства диагностируемого объекта, принято
называть "глубинным" знанием.Диагностирование, основанное на моделях анализируемых объектов, использует не столько эмпирический опыт эксперта, сколько более или менее полную и непротиворечивую теорию корректного поведения этих объектов. Идея состоит в том, чтобы, располагая на входе данными о наблюдаемых отклонениях в поведении, высказать предположение об одном или нескольких возмущениях в описании системы, которые могли бы объяснить эти отклонения.
Очевидные преимущества подхода,
при котором сначала принимаются во внимание знания о принципах поведения объекта,
а уже затем эмпирические знания, состоят в следующем.
Используемый метод анализа причинно-следственных связей не зависит от самого анализируемого объекта, а следовательно, отпадает необходимость в трудоемкой настройке механизма логического вывода для каждого отдельного приложения.
Поскольку требуется знание только о корректном поведении объекта, потенциально метод должен сработать и при диагностировании неисправностей, которые ранее не возникали и незнакомы эксперту-человеку.
Прототипом подобного рода диагностических экспертных систем можно считать программу DART [Genesereth, 1984]. Хотя предметной областью, для которой предназначалась эта программа, является анализ цифровых схем, но использованные в ней язык представления знаний и механизм логического вывода более или менее независимы от этой предметной области. Для представления описания конструкции диагностируемого устройства используются формализм исчисления предикатов и форма доказательства теорем, с помощью которых формируются множества "подозрительных" компонентов и тестов, призванных подтвердить или опровергнуть гипотезы о причинах неисправностей. Метод решения проблем, использованный в DART, опирается на три упрощающих допущения.
(1) Предполагается, что связи между компонентами функционируют правильно, и задача состоит в том, чтобы отыскать те компоненты, неисправность которых может объяснить наблюдаемые симптомы неправильной работы устройства.
(2) Отказы не носят случайного во времени характера, т.е. все компоненты в процессе выполнения диагностических тестов работают стабильно (правильно или неправильно — это уже другой вопрос).
(3) В устройстве имеется единственный отказ.
Каждое из этих предположений, конечно же, очень ограничивает возможность практического применения системы, но в работе [De Kleer and Williams, 1987] было показано, что использование систем отслеживания истинности предположений, основанных на анализе допущений, поможет снять третье из перечисленных ограничений. Это было продемонстрировано в программе GDE (General Diagnostic Engine — система диагностирования общего назначения).
В системе диагностирования, допускающей наличие нескольких неисправностей в устройстве, приходится иметь дело с экспоненциальным ростом пространства гипотез. Чтобы преодолеть возникающие при этом сложности, нужно формировать гипотезы в определенном порядке, принимая во внимание их "конструктивность", а затем выполнять такие процедуры тестирования, которые позволят выбрать из набора конкурирующих гипотез наиболее подходящую, проведя при этом минимальное количество дополнительных измерений. Реализуется такой процесс с помощью комбинации методов отслеживания истинности предположений, основанных на анализе допущений, и методов вероятностного логического вывода.
Как было показано ранее в этом же разделе, методы отслеживания истинности предположений, основанные на анализе допущений, имеют дело с решеткой сред — альтернативных состояний модели мира, которые согласуются с некоторой теорией, но используют при этом отличающиеся допущения. В диагностических приложениях такой неявной теорией является описание диагностируемого устройства, а альтернативные состояния модели мира характеризуются различными комбинациями отказавших компонентов устройства. Если устройство состоит из п компонентов, то теоретически может существовать 2" комбинаций отказов компонентов. Решетка вариантов сред является перечислимым множеством присоединений: элемент с наименьшим номером соответствует отсутствию отказов в компонентах, а элемент с наибольшим номером — отказу всех компонентов устройства. Каждая такая среда называется кандидатом, т.е. гипотезой о том, что именно произошло в неисправном устройстве. Вся решетка сред при такой постановке проблемы будет представлять собой пространство кандидатов.
Если устройство работает нормально, то гипотеза, соответствующая кандидату' с наименьшим номером, прекрасно "объясняет" наблюдаемую ситуацию. Если наблюдаются какие-либо отклонения от нормального функционирования устройства, то наблюдаемые проявления можно считать свидетельствами в пользу той или иной гипотезы в пространстве кандидатов. Поскольку объем этого пространства связан с количеством компонентов в анализируемых устройствах экспоненциальной зависимостью, необходимо использовать в нем какой-либо метод эффективного поиска кандидатов.
Ключевым понятием для такого метода должно быть конфликтующее множество — множество таких компонентов, которые в данной ситуации (т.е. при данных симптомах) не могут одновременно быть исправными. Конфликтующее множество, таким образом, это именно то множество допущений, которое в системе отслеживания истинности предположений, основанной на анализе допущений, формирует среды, несовместимые с данными. Их можно определить, формируя дедуктивное замкнутое выражение для среды и данных, а затем выискивая в нем противоречие. Главная цель системы отслеживания истинности предположений состоит при этом в том, чтобы идентифицировать все минимальные конфликтующие множества. После этого можно определить минимальное множество отказавших компонентов, которое объяснит все наблюдаемые проявления ненормальной работы устройства.
В качестве простого примера рассмотрим решетку сред, представленную на рис. 19.6. В этой решетке C1, C2 и СЗ— компоненты анализируемого устройства. Пусть S — множество наблюдаемых проявлений ненормальной работы этого устройства. Предположим, нам известно, что если наблюдается множество проявлений S, то С1 и С2 не могут быть исправными одновременно, а также С1 и СЗ. Тогда можно выделить среды, помеченные на схеме решетки значками 0, С2 и СЗ (они выделены на схеме как несовместные). Каждая из этих сред имеет какое-либо запрещенное сочетание исправных компонентов. Все другие среды являются кандидатами в пространстве гипотез, но очевидно, что минимальные множества среди них — (С1} и {С2, СЗ}.
В системе отслеживания истинности предположений используется несколько стратегий управления обработкой пространства кандидатов, например:
стратегия, основанная на предоставлении преимущества тем гипотезам, которые поясняются проще всего; поиск решения начинается с минимальных по объему (количеству элементов) конфликтных множеств;
сохранение в системе просмотренной цепочки логического вывода, что позволяет исключить ее повторный просмотр.
В системе GDE также используется мера неопределенности, основанная на теоретико-информационном подходе, с помощью которой выясняется, какие измерения следует выполнить в анализируемой системе. Наилучшей полагается такая измерительная процедура, которая минимизирует энтропию (см. об этом в главе 20), т.е. та, которая вносит наибольшее разнообразие в набор значений вероятностей кандидатов. Предполагается, что априорная вероятность отказа отдельных компонентов известна и что отказы компонентов в вероятностном смысле независимы. Эти же вероятности используются при определении порядка формирования гипотез-кандидатов.

Рис. 19.6. Решетка сред, представляющая пространство кандидатов. Несовместные контексты выделены утолщенным контуром, а минимальные кандидаты заштрихованы
Сравнение различных вариантов организации систем отслеживания истинности предположений
Функции компонента отслеживания истинности предположений в контексте более общей программы поиска решения проблемы можно сформулировать следующим образом:
кэшировать логический вывод, выполненный решателем проблем, чтобы однажды сформулированное заключение не пришлось выводить повторно;
предоставить в распоряжение решателя проблем средства формирования конструктивных допущений и анализа полезности заключений, выведенных на основе таких допущений;
анализировать и устранять возможные противоречия в моделях среды.
Подходы к построению системы отслеживания истинности предположений, предлагаемые Дойлом и Мак-Аллестером, можно использовать для нахождения единственного решения проблемы, удовлетворяющего заданным ограничениям. Прекрасным примером использования этого подхода на практике является экспертная система VT, описанная в главе 15,
Если же необходимо отыскать несколько вариантов решения или все возможные решения, понадобится более сложный механизм отслеживания. Работа с единственным состоянием сети зависимостей не позволяет выполнять сравнение альтернативных вариантов решения проблемы. Например, при выполнении дифференциального диагностирования желательно сравнивать конкурирующие гипотезы, поскольку среди них может оказаться такая, которая позволит объяснить все наблюдаемые проявления.
Подход, предложенный Де Клером, ориентирован именно на отыскание всех вариантов решения, удовлетворяющих заданным ограничениям. Если среди всех возможных решений система должна будет выбрать "наилучшее" по какому-либо критерию, понадобится оснастить ее дополнительным механизм управления.
Рекомендуемая литература
Сети зависимостей рассматриваются в работе [Charniak et al., 1987]. Статьи [De Kleer, 1986] и [Doyle, 1979] довольно сложные для неподготовленного читателя, а потому я бы посоветовал начинать углубленное изучение этой темы с работы [Forbus and De Kleer, 1993]. В этой же книге вы найдете и листинги множества программ, которые демонстрируют использование описанных в ней методов. Читатели, интересующиеся теоретическим обоснованием методов отслеживания истинности предположений, могут найти много интересного для себя в книге [Ginsberg, 1987] и сборнике статей [Martins and Reinfrank, 1991].