Функции 2-х переменных
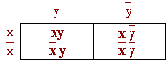
Диаграмма – матрица, столбцам и строкам которой приписывается смысл переменных, входящих в функцию в прямом или инверсном виде.
В клетках матрицы ставится произведение, образованное из букв, которыми названы строки и столбцы матрицы.
Обратим внимание на то, что данная матрица сразу указывает на возможную склейку произведений, входящих в выражение функции.
Так склейке подлежат все произведения, расположенные в соседних по вертикали и горизонтали клетках.
xy склеивается с xy и с xy;
xy склеивается с xy и с xy;
xy склеивается с xy и с xy;
xyсклеивается с xy и с xy;
Более того, эта же диаграмма дает и результат склейки: это название или строки, или столбца. При минимизации по данному методу заполняется диаграмма функции 2-х переменных по следующему правилу: если то или иное произведение входит в СДНФ функции, то в соответствующую ему клетку диаграммы ставится единица, и нуль – в противном случае. Если в диаграмме находится хотя бы две соседние единицы, то это означает, что два произведения склеиваются, а результатом склейки является произведение (в данном случае из одной буквы), именем которого названа данная строка или столбец.
Пример:
f(x,y) = xy


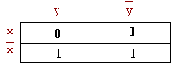
Выделим в диаграмме соседние единицы, и результат склейки дает минимальную форму функции: fmin(x,y) = x

Заметим, что результатом склейки является результат покрытия конституент единицы исходной функции простыми импликантами. В данном случае переменными, которыми названы строки и столбцы диаграммы.
Функции 3-х переменных
Для минимизации функций, зависящих от трех переменных, применяется следующая диаграмма:
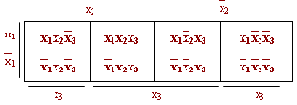
Из диаграммы видно, что склейке подлежат все произведения, расположенные в соседних клетках, а также в клетках, расположенных на краях диаграммы. Результат склейки – есть произведения, содержащее на одну букву меньше. Видно также, что возможна и дальнейшая склейка, однако уже между произведениями, расположенными во взаимно перпендикулярном направлении.
Рассмотрим, например, левую половину диаграммы:
| x1x2x3 | x1x2x3 |
| x1x2x3 | x1x2x3 |
Склеим попарно произведения, стоящие в строках:
| x1x2 | x1x2 |
| x1x2 | x1x2 |
Теперь видим, что можно произвести дальшейшую склейку, но произведений, стоящих в столбцах матрицы:
| x2 | x2 |
| x2 | x2 |
Как видно, результат склейки – произведение x2. Именно эта переменная покрывает все четыре конституенты единицы СДНФ функции.
Подобное же утверждение справедливо и для конституент, расположенных в строках и столбцах диаграммы по краям таблицы.
Таким образом, при поиске минимальной формы необходимо считать левый край таблицы склеенным с правым. Говорят, что для наглядности можно условно данную диаграмму представить нанесенной на поверхность цилиндра.
Пример:
f(x1x2x3) = x1x2x3

x1x2x3



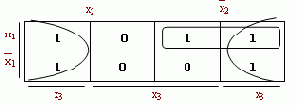
fmin(x1x2x3) = x3

Видим, что две единицы, соответствующие конституентам x1x2x3 и x1x2x3, покрываются произведением x1x2.
Функции 4-х переменных
Для функций 4-х переменных применяются диаграммы следующего вида:
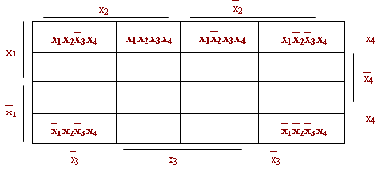
Все, что было сказано относительно функций 2-х, 3-х переменных справедливо и в данном случае. Но данная диаграмма обладает дополнительной особенностью: при поиске минимальной формы функции необходимо считать склееными правый край с левым и верхний с нижним.
Говорят, что для удобства целесообразно считать данную диаграмму написанной на поверхность тора.
Пример:
f(x1,x2,x3,x4) = x1x2x3x4




x1x2x3x4

Составим диаграмму:
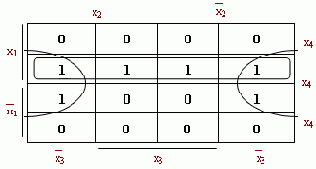
fmin(x1,x2,x3,x4) = x1x4

Заметим, что на основании свойства диаграммы четыре единицы, стоящие в угловых клетках диаграммы соответствуют конституентам, которые склеиваются между собой.
Итак, дадим формализированное описание метода.
Опредение. Правильной конфигурацией ранга К называется совокупность единиц (нулей), образующая прямоугольник площадью 2к.
Для минимизации функции, зависящей от n аргументов, отыскиваются правильные конфигурации вначале n-1 ранга, затем n-2 ранга и т.д.
Далее определяется накрытие найденных правильных конфигураций совместной проекцией соответствующих строк и столбцов, которая выделяет данную правильную конфигурацию.
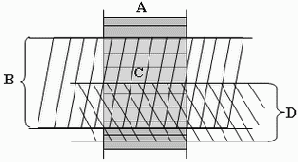
Рис. 4.1. Определение правильных конфигураций
C– правильная конфигурация
A,B,D– проекции конфигурации
А*В– результат склеек
Метод импликантных матриц
Для поиска минимальной формы функции пользуются методом импликантных матриц. Существо метода заключается в следующем: составляется импликантная матрица, колонки которой именуются конституентами единицы, а строки – простыми импликантами. Затем находится минимальное покрытие всех конституент единицы простейшими импликантами. При этом ищется такая минимальная совокупность простых импликант, которые совместно покрывают все конституенты единицы исходной функции. Факт покрытия отмечается в клетке матрицы символом * (звездочка) в случае, когда импликанта покрывает соответствующую конституенту (является ее собственной частью). Из всех простых импликант выбираются вначале только такие, которые только одни покрывают конституенты единицы (в колонке матрицы только один символ покрытия), затем производится перебор.
Пример:
|
r |
* |
* |
* | ||||||||
|
p |
* |
* |
* | ||||||||
|
q |
* |
* | |||||||||
|
m |
* | ||||||||||
|
n |
* |
* |
Из матрицы видно, что в минимальную форму функции обязательно войдут импликанты n (покрывает конституенту F), импликанта r (покрывает конституенту D). То же справедливо отностительно импликанты p. Что касается остальных, то нужно выбрать минимальную совокупность.
Итак:
f1min = n






Т.е. данная функция имеет две одинаково минимальные формы.
Замечание: важным обстоятельством, усложняющим минимизацию функций, является присутствие перебора различных вариантов при поиске оптимального покрытия.
Метод Квайна – Мак – Класки
Основное неудобство метода Квайна состоит в том, что при поиске простых импликант необходимо производить попарные сравнения вначале всех конститутент единицы, затем полученных в результате склеивания произведений.
С целью упрощения этой процедуры Мак – Класки предложил алгоритм, существо которого сводится к следующему:
вводится понятие цифрового эквивалента для каждого произведения по следующему правилу: некоторому произведению ставится в соответствие цифровой эквивалент с использованием цифр 0 и 1 и – (прочерк). Переменной, входящей в произведение в прямом виде ставится в соответствие единица (1), в инверсном – нуль (0), отсутствие переменной обозначается прочерком;в любом произведении переменные располагаются только в одном порядке, а именно – по возрастанию индексов;склейке подлежат только те произведения, в которых прочерки расположены соответственно, количество нулей (или единиц) отличается на единицу и они расположены так же соответственно.
Пример:
Произведению x1x2x4 для функции, зависящей от пяти переменных нужно поставить в соответствие следующий цифровой набор: x1x2x4: 11-0-
Приведем графическое изображение процесса поиска простых импликант для функции, представленной в следующей СДНФ:
f(x1x2x3x4) = x1x2x3x4



запишем выражение функции в виде дизъюнкции цифровых эквивалентов:
f(x1x2x3x4) = 1101



При графическом способе отыскания простых импликант вначале все цифровые наборы разбивают на группы и располагают эти группы в следующем порядке: вначале идет группа цифровых эквивалентов, содержащих только нули (такой набор может быть один), затем следует группа с наборами, содержащими по одной единице, затем по две и т.д. Сравнением наборов соседних групп устанавливается возможность склейки, делается необходимая пометка и пишется результат склейки. Процесс продолжается до тех пор, пока возможны склейки. Все несклеенные наборы, а также конечные результаты склейки дают простые импликанты. Расшифровка полученных цифровых эквивалентов - очевидна.
Для нашего примера это выглядит так:
1000 | * | 10-0 | - |
0101 | * | ||
1010 | * | -101 | - |
1101 | * |
10-0 и -101, т.е. f(x1x2x3x4) = x1x2x4

Минимизирующие диаграммы
Этот метод графической минимизации был изложен Карно, который ввел в употребление специальные карты. Эти карты позволяют для функции, зависящей от небольшого числа аргументов (до пяти - шести) находить результаты всех возможных склеек. Карты впоследствии были усовершенствованы Вейчем, а сам метод иногда именуется как метод минимизации с помощью диаграмм Вейча.
Рассмотрим существо способа для функций, зависящих от 2, 3 и 4-х переменных.
Свойства диаграмм Вейча
С помощью диаграмм Вейча можно находить:
минимальную форму по СКНФминимальную форму по ДНФ и КНФ функциивсе одинаково минимальные формыминимальную форму неполностью определенных функций.
Пусть f(x1x2x3) задана не в виде СДНФ, а в ДНФ:
f(x1x2x3) = x1x2


Заполним соответствующую диаграмму:

Так как x1x2 = x1x2 (x3


Поэтому: fmin(x1,x2,x3) = x2x3


Преимущество метода: простота и наглядность для небольшого числа аргументов.
Недостатки: неприменяемость метода для большого числа аргументов (> 6) вследствие сложности диаграмм и потери наглядности.