Учебник по промышленной статистике
Анализ процессов
Анализ производственных процессов
- Выборочные планы
- Основное назначение
- Методы вычислений
- Средние для гипотез Н0 и Н1
- Вероятности ошибок альфа и бета
- Планы с фиксированным объемом выборки
- Последовательные выборочные планы
- Выводы
- Анализ пригодности процессов
- Введение
- Методы вычислений
- Индексы (показатели) пригодности
- Качество и пригодность процесса
- Использование экспериментов для повышения пригодности
- Проверка предположения о нормальности распределения
- Доверительные границы
- Повторяемость и воспроизводимость измерений
- Введение
- Методы вычислений
- Графики повторяемости и воспроизводимости
- Компоненты дисперсии
- Выводы
- Негауссовские распределения
- Введение
- Подгонка методом моментов
- Качество подгонки: графики квантилей и вероятностей
- Негауссовские индексы пригодности (метод процентилей)
- Анализ Вейбулла, надежность и времена отказов
- Основные задачи
- Распределение Вейбулла
- Цензурированные наблюдения
- Двух- и трехпараметрическое распределение Вейбулла
- Оценка параметров
- Критерии согласия
- Интерпретация результатов
- Группированные данные
- Изменения порядка времен отказов для многократно цензурированных данных
- Функция распределения Вейбулла, надежность и функции риска
Планы выборочного контроля подробно обсуждаются в работах Duncan (1974) и Montgomery (1991). Большинство процедур оценивания пригодности процессов (и соответствующих показателей) были сравнительно недавно заимствованы из Японии и внедрены в США (Kane, 1986); они обсуждаются в трех превосходных практических руководствах Bohte (1988), Hart and Hart (1989) и Pyzdek (1989); подробные обсуждения этих методов можно также найти в работе Montgomery (1991).
- Выборочные планы
- Основное назначение
- Методы вычислений
- Средние для гипотез Н0 и Н1
- Вероятности ошибок альфа и бета
- Планы с фиксированным объемом выборки
- Последовательные выборочные планы
- Выводы
- Анализ пригодности процессов
- Введение
- Методы вычислений
- Индексы (показатели) пригодности
- Качество и пригодность процесса
- Использование экспериментов для повышения пригодности
- Проверка предположения о нормальности распределения
- Доверительные границы
- Повторяемость и воспроизводимость измерений
- Введение
- Методы вычислений
- Графики повторяемости и воспроизводимости
- Компоненты дисперсии
- Выводы
- Негауссовские распределения
- Введение
- Подгонка методом моментов
- Качество подгонки: графики квантилей и вероятностей
- Негауссовские индексы пригодности (метод процентилей)
- Анализ Вейбулла, надежность и времена отказов
- Основные задачи
- Распределение Вейбулла
- Цензурированные наблюдения
- Двух- и трехпараметрическое распределение Вейбулла
- Оценка параметров
- Критерии согласия
- Интерпретация результатов
- Группированные данные
- Изменения порядка времен отказов для многократно цензурированных данных
- Функция распределения Вейбулла, надежность и функции риска
Планы выборочного контроля подробно обсуждаются в работах Duncan (1974) и Montgomery (1991).
Большинство процедур оценивания пригодности процессов (и соответствующих показателей) были сравнительно недавно заимствованы из Японии и внедрены в США (Kane, 1986); они обсуждаются в трех превосходных практических руководствах Bohte (1988), Hart and Hart (1989) и Pyzdek (1989); подробные обсуждения этих методов можно также найти в работе Montgomery (1991).
Подробные инструкции по вычислению и интерпретации показателей пригодности даются также в издании Fundamental Statistical Process Control Reference Manual,
опубликованном ASQC (Аmerican Society for Quality Control) и AIAG (Automotive Industry Action Group, 1991; далее это руководство упоминается как ASQC/AIAG, 1991). Методы повторяемости и воспроизводимости (R & R) обсуждаются в работах Grant and Leavenworth (1980), Pyzdek (1989), а также в Montgomery (1991); более подробное обсуждение этой темы (оценивание дисперсии) приводится также в работе Duncan (1974).
Подробные инструкции по проведению и анализу экспериментов по повторяемости и воспроизводимости (R & R) содержатся в руководстве Measurement Systems Analysis Reference Manual, опубликованном ASQC/AIAG (1990). Краткое описание этих процедур можно найти в следующих разделах. Дополнительные сведения об анализе планов со случайными эффектами и оценке компонент дисперсии можно найти в разделе Компоненты дисперсии.
Планы выборочного контроля
- Основное назначение
- Методы вычислений
- Средние для гипотез H0 и H1
- Вероятности ошибок альфа и бета
- Планы с фиксированным объемом выборки
- Последовательные выборочные планы
- Выводы
Основное назначение
Основное назначение
Общая проблема, с которой сталкиваются инженеры по контролю качества, состоит в том, чтобы определить, сколько изделий из партии (например, полученной от поставщика) необходимо исследовать, чтобы быть уверенными в том, что изделия этой партии обладают приемлемым качеством.
Допустим, что у вашей автомобильной компании есть поставщик поршневых колец для небольших двигателей, и ваша цель – разработать процедуру выборочного контроля поршневых колец в присылаемых партиях, обеспечивающую требуемое качество. В принципе эта проблема сходна с проблемой, рассмотренной в разделе Контроль качества, где обсуждаются вопросы статистического контроля качества промышленной продукции.
Выборочный контроль при приемке.
Выборочный контроль при приемке.
Процедуры выборочного контроля применяются в том случае, когда нужно решить, удовлетворяет ли определенным спецификациям партия изделий, не изучая при этом все изделия. В силу природы проблемы – принимать или не принимать партию изделий – эти методы иногда называют статистическим приемочным контролем (acceptance sampling)
Преимущества над полным контролем.
Преимущества над полным контролем.
Очевидное преимущество выборочного контроля над полным (сплошным) контролем партии состоит в том, что изучение только выборки (а не всей партии) требует меньшего времени и финансовых затрат. В некоторых случаях исследование изделия является разрушающим (например, испытание стали на предельную прочность), и сплошной контроль уничтожил бы всю партию. Наконец, с точки зрения управления производством, отбраковка всей партии или поставки от данного поставщика (на основании выборочного контроля) вместо браковки лишь определенного процента дефектных изделий (на основании сплошного контроля) часто заставляет поставщиков строже придерживаться стандартов качества.
Методы вычислений
Методы вычислений
В принципе вычислительный подход к вопросу о том, насколько большую выборку следует взять, несложен. В разделе Элементарные понятия статистики обсуждается понятие выборочного распределения. Если взять повторные выборки определенного объема из совокупности, скажем, поршневых колец, и вычислить их средние диаметры, то распределение этих средних значений будет приближаться к нормальному распределению с определенным средним значением и стандартным отклонением (или стандартной ошибкой; для выборочных распределений термин “стандартная ошибка” предпочтительнее, чтобы отличать изменчивость средних значений от изменчивости изделий в генеральной совокупности).
К счастью, нет необходимости брать повторные выборки из совокупности, чтобы оценить среднее значение и изменчивость (стандартную ошибку) выборочного распределения. Располагая хорошим представлением (оценкой) того, какова изменчивость (стандартное отклонение, или сигма) в данной совокупности, можно вывести выборочное распределение среднего значения. В принципе этой информации достаточно, чтобы оценить объем выборки, необходимый для обнаружения некоторого изменения качества (по сравнению с заданными спецификациями). Опуская детали соответствующих вычислительных процедур, рассмотрим вопрос о том, какие параметры должен иметь в своем распоряжении инженер, чтобы провести соответствующие вычисления.
Средние для гипотез H0 и H1
Средние для гипотез H0 и H1
Чтобы формализовать процесс проверки, скажем, партии поршневых колец, нужно сформулировать две альтернативных гипотезы. Во-первых, можно предположить, что средние диаметры поршневых колец удовлетворяют техническим условиям. Эта гипотеза называется нулевой гипотезой (H0). Альтернативная гипотеза (H1), состоит в том, что диаметры поршневых колец отклоняются от технических условий больше, чем на определенную величину. Заметим, что можно сформулировать такого рода гипотезы не только для измерений, типа диаметров поршневых колец, но и для качественных характеристик (признаков). Например, можно предположить (H1), что доля дефектных изделий в партии превышает определенный процент (нулевая гипотеза). Естественно, что чем больше различие между H0 и H1, тем меньшего объема выборка необходима для обнаружения этого различия (см. раздел Элементарные понятия статистики).
Вероятности ошибок альфа и бета
Вероятности ошибок альфа и бета
Возвращаясь к примеру с поршневыми кольцами, заметим, что существует два рода ошибок, которые можно сделать при проверке партии поршневых колец. Во-первых, можно ошибочно отвергнуть H0, то есть забраковать партию, решив, что диаметры поршневых колец отклоняются от заданных спецификаций.
Вероятность совершить такую ошибку обычно называется вероятностью ошибки первого рода (типа альфа). Вторая ошибка, которую можно сделать, –ошибочно не отвергнуть H0 (принять партию поршневых колец), когда на самом деле средний диаметр поршневых колец отклоняется от требуемого на определенную величину. Вероятность этой ошибки обычно называется вероятностью ошибки второго рода (типа бета). Ясно, что чем большая уверенность в правильном решении вам нужна, то есть чем ниже будут заданы вероятности ошибок первого и второго рода, тем большего объема выборки потребуются; фактически, чтобы быть уверенным на 100%, придется измерить каждое поставленное вашей компании поршневое кольцо.
Планы с фиксированным объемом выборки
Планы с фиксированным объемом выборки
Чтобы построить простой план выборочного контроля, сначала принимается решение об объеме выборки, основанное на средних значениях в предположении справедливости гипотез H0 или H1 и конкретных значениях вероятностей ошибок типа альфа и бета. Затем берется одна выборка этого фиксированного объема и на основании значения этого выборочного среднего принимается решение принять или отвергнуть данную партию. Такая процедура называется контролем с фиксированным объемом выборки (fixed sampling plan).
Кривая операционных характеристик (ОХ).
Кривая операционных характеристик (ОХ).
Мощность плана выборочного контроля с фиксированным объемом выборки можно представить с помощью кривой операционных характеристик. На графике вероятность отвергнуть H0 (и принять H1) откладывается по оси ординат как функция отклонения фактических значений, отложенных по оси абсцисс, от заданного (номинального) значения. Эта вероятность, разумеется, равна единице минус вероятность ошибки второго рода (ошибочно отвергнуть H1 и принять H0) и называется мощностью обнаружения отклонений для плана выборочного контроля с фиксированным объемом выборки. На графике показаны функции мощности для выборок разного объема.
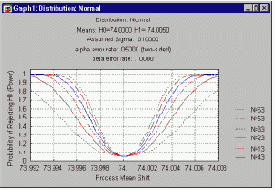
Последовательные выборочные планы
Последовательные выборочные планы
В качестве альтернативы контролю с фиксированным объемом выборки можно случайным образом выбирать отдельные поршневые кольца и записывать их отклонения от номинала. Продолжая измерять каждое следующее выбранное поршневое кольцо, вычисляют текущую общую сумму отклонений от номинала (суммарное отклонение). Ясно, если гипотеза H1 верна, иными словами, если средний диаметр поршневых колец в данной партии отличается от номинального, то следует ожидать постепенного увеличения или уменьшения совокупного (накопленного) отклонения в зависимости от того, больше или меньше средний диаметр колец в партии, чем номинал. Такого рода последовательный выборочный контроль более чувствителен, чем контроль, основанный на выборке фиксированного объема. На практике отбор изделий продолжается до тех пор, пока партия не будет принята или забракована.
Применение последовательного выборочного контроля.
Применение последовательного выборочного контроля.
Вначале обычно строится график, на котором показывается накопленное отклонение от номинала (откладываемое на оси ординат) для последовательно отбираемых изделий (например, поршневых колец, номер которых в выборке откладывается по оси абсцисс). Затем на графике проводятся два набора прямых, обозначающих "коридор". Отбор изделий продолжается до тех пор, пока совокупное отклонение остается внутри данного коридора.
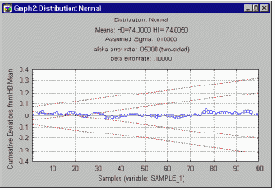
Отбор прекращается, если накопленное отклонение выходит из коридора. Если это значение поднимается выше верхней линии или опускается ниже нижней линии, партия забраковывается. Если накопленное отклонение выходит из коридора внутрь, то есть приближается к средней линии, партия принимается (это указывает на практически нулевое отклонение от номинала). Обратите внимание, что внутренняя область начинается с некоторого определенного номера, который соответствует минимальной величине объема выборки, необходимой для принятия решения о приемке партии изделий (при заданных вероятностях ошибки).
Выводы
Выводы
Итак, цель статистического контроля – использование статистического "заключения" для приемки или отбраковки всей партии изделий на основании изучения лишь сравнительно небольшого числа изделий из этой партии.
Преимущество применения статистических рассуждений при принятии такого решения состоит в возможности вычисления или задания в явном виде вероятностей принять ошибочное решение.
Всегда, когда возможно, последовательный выборочный контроль следует предпочесть контролю с фиксированным объемом выборки, так как он обладает большей мощностью. В большинстве случаев для принятия решения с той же степенью уверенности последовательный выборочный контроль в среднем требует анализа меньшего числа выборок, чем контроль с заранее фиксированным объемом выборки.
| Оглавление |
Анализ пригодности процесса
- Введение
- Методы вычислений
- Индексы (показатели) пригодности
- Пригодность и качество процесса
- Использование экспериментов для повышения пригодности
- Проверка предположения о нормальности распределения
- Доверительные границы
Введение
См. также раздел Негауссовские распределения.
В разделе Контроль качества описано много методов оценки качества производственного процесса. Однако как только процесс становится управляемым, возникает следующий вопрос: "в какой степени долговременное поведение процесса удовлетворяет техническим условиям и целям, поставленным руководством?" Возвращаясь к примеру с поршневыми кольцами, можно спросить: какое количество использованных поршневых колец попадает в границы конструктивного допуска? В более общих терминах вопрос ставится так: "насколько данный процесс (или поставщик) способен производить изделия, удовлетворяющие техническим условиям?" Большинство описанных здесь процедур и характеристик производства сравнительно недавно внедрены в США компанией "Форд Моторс" (Kane, 1986). Они позволяют оценить пригодность процесса с помощью осмысленных показателей.
Сначала мы обсудим вычисление и интерпретацию показателей пригодности процесса для случая нормального распределения. Если распределение параметров качества не подчиняется нормальному закону, то возможны модифицированные показатели, вычисленные на основе квантилей подходящего аппроксимирующего распределения из числа негауссовских распределений (например, Вейбулла, логарифмически нормального, бета, гамма и др.) или из семейства распределений общего вида с помощью метода моментов.
Важное замечание.
Важное замечание.
Заметим, что нет смысла изучать пригодность производственного процесса, если он не управляем. Иными словами, если средние значения последовательных выборок сильно флуктуируют или явно находятся вне заданного допуска, то вначале нужно решить проблемы качества. Следовательно, первый шаг к организации высококачественного процесса производства состоит в том, чтобы сделать процесс управляемым с помощью методов, описанных в разделе Контроль качества.
Методы вычислений
Методы вычислений
Если процесс управляем, то можно ставить вопрос о его пригодности. Ответ на этот вопрос основывается на "статистических" рассуждениях и близок к обсуждавшейся ранее проблеме выборочного контроля. Возвращаясь к примеру с поршневыми кольцами, заметим, что если дана выборка определенного объема, то можно оценить стандартное отклонение процесса производства поршневых колец. Затем можно построить гистограмму распределения диаметров поршневых колец. Если распределение диаметров нормальное, то можно сделать выводы о доле поршневых колец, попадающих в границы допуска.
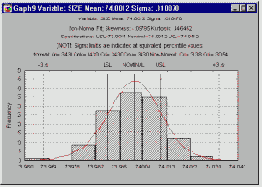
Для негауссовских распределений используется метод процентилей. Рассмотрим основные показатели пригодности, наиболее часто используемые для анализа производственных процессов.
Индексы (показатели) пригодности процесса
Индексы (показатели) пригодности процесса
Размах процесса.
Размах процесса.
Как правило, сначала находят границы ±3 сигма по обе стороны от номинала. На самом деле границы сигма должны быть те же самые, что применяются для обеспечения управляемости процесса с помощью контрольных карт (см. Контроль качества). Эти границы обозначают размах процесса. Если используется интервал ±3 сигма, то в предположении нормальности распределения можно сделать вывод о том, что примерно 99% всех поршневых колец находятся в этих границах.
Границы допуска НГД, ВГД.
Границы допуска НГД, ВГД.
Обычно технические условия задают некий диапазон допустимых значений. В данном примере считается приемлемым, если значения диаметров поршневых колец лежат в пределах 74.0 ± .02 мм.
Таким образом, нижняя граница допуска (lower specification limit – LSL) для данного процесса равна 74.0 - 0.02 = 73.98 , верхняя граница допуска (upper specification limit – USL) равна 74.0 + 0.02 = 74.02. Разность между НГД и ВГД называется размахом допуска (specification range).
Потенциальная пригодность (Cp).
Потенциальная пригодность (Cp).
Это простейший и самый естественный показатель пригодности производственного процесса. Он определяется как отношение размаха допуска к размаху процесса; при использовании границ ±3 сигма данный показатель можно выразить в виде
Cp = (ВГД-НГД)/(6*сигма)
Данное отношение выражает долю размаха кривой нормального распределения, попадающую в границы допуска (при условии, что среднее значение распределения является номинальным, то есть процесс центрирован, см. ниже).
В работе Bhote (1988) сообщается, что до повсеместного внедрения методов статистического контроля качества (до 1980 г.) обычное качество производственных процессов в США составляло примерно Cp = .67. Иными словами, два хвоста кривой нормального распределения, каждый из которых содержит примерно 15.5% общего количества изделий, попадали за границы допуска. В конце 80-х годов лишь около 30% производств в США находились на этом или еще худшем уровне качества (см. Bhote, 1988, стр. 51). В идеале, конечно, было бы хорошо, если бы этот показатель превышал 1, т.е. хотелось бы достигнуть такого уровня пригодности процесса, чтобы никакое (или почти никакое) изделие не выходило за границы допуска. Любопытно, что в начале 80-ых годов японская промышленность приняла в качестве стандарта Cp = 1.33! Пригодность процесса, требуемая для изготовления высокотехнологичных изделий, еще выше; компания Minolta установила показатель Cp = 2.0 как минимальный стандарт для себя (Bhote, 1988, стр. 53) и как общий стандарт для своих поставщиков. Заметим, что высокая пригодность процесса обычно приводит к более низкой, а не к более высокой себестоимости, если учесть затраты на рекламацию, связанную с низким качеством производимой продукции.
Этот пункт мы кратко обсудим ниже.
Отношение пригодности (Cr).
Отношение пригодности (Cr).
Этот индекс является обратным к показателю Cp и вычисляется как отношение 1/Cp.
Нижняя/верхняя потенциальная пригодность: Cpl, Cpu.
Нижняя/верхняя потенциальная пригодность: Cpl, Cpu.
Недостаток показателя Cp (и Cr) состоит в том, что он может дать неверную информацию о производственном процессе в том случае, если среднее процесса отличается от номинального, иными словами, если процесс не центрирован. Нецентрированность или смещенность процесса производства можно выразить следующим образом. Сначала можно вычислить верхний и нижний показатели пригодности, чтобы отразить отклонение наблюдаемого среднего процесса от НГД и ВГД. Приняв в качестве размаха процесса границы ±3 сигма, вычислим следующие показатели:
Cpl = (Среднее - НГД)/3*сигма
и
Cpu = (ВГД - Среднее)/3*сигма
Ясно, что если эти значения не совпадают, то процесс не центрирован.
Поправка на нецентрированность(K).
Поправка на нецентрированность(K).
Можно скорректировать индекс Cp, чтобы учесть смещение. А именно, вычислим:
k = abs(Номинал - Среднее)/(1/2(ВГД-НГД))
Этот поправочный множитель выражает отношение нецентрированности (номинал минус среднее) к допуску.
Подтвержденное качество (Cpk).
Подтвержденное качество (Cpk).
Наконец, Cp можно скорректировать, внеся поправку на нецентрированность посредством вычисления
Cpk = (1-k)*Cp
Если процесс идеально центрирован, то k равно нулю и Cpk равно Cp. Однако когда процесс смещается от номинального значения, k увеличивается, и Cpk становится меньше Cp.
Потенциальная пригодность II: Cpm.
Потенциальная пригодность II: Cpm.
Недавно введенная модификация показателя Cp (Chan, Cheng, and Spiring, 1988) направлена на уточнение оценки сигмы с целью учесть влияние случайной нецентрированности. При этом вычисляется другое значение, а именно, Сигма2:
Сигма2 = {

где
Сигма2- другая оценка сигма,
xi - значение i-го выборочного наблюдения,
Номинал - значение номинала,
n - число наблюдений в выборке.
Затем можно использовать эту оценку параметра сигма при вычислении Cp по тем же формулам, что и прежде. Полученный показатель будет обозначаться Cpm.
Качество и пригодность процесса
Качество и пригодность процесса
При контроле процесса с помощью карт контроля качества (например, X- или R карты; см. раздел Контроль качества) часто бывает полезно вычислять показатели пригодности процесса. Когда набор данных состоит из нескольких выборок, то можно вычислить два разных показателя изменчивости. Один из них – обычное стандартное отклонение для всех наблюдений, не принимающее в расчет, что данные состоят из нескольких выборок; другой показатель оценивает собственный разброс процесса по изменчивости внутри выборки. Например, при построении X- или R карт можно использовать обычную оценку R_/d2 для сигмы процесса (см., например, Duncan, 1974; Montgomery, 1985). Заметим, однако, что эта оценка применима только тогда, когда процесс статистически устойчив. Подробное обсуждение различия между общей и собственной изменчивостью процесса содержится в справочном руководстве ASQC/AIAG (ASQC/AIAG, 1991, стр. 80).
Когда при стандартных вычислениях пригодности используется общая изменчивость процесса, полученные показатели обычно называют показателями качества процесса (process performance) (поскольку они описывают фактическое поведение процесса), тогда как показатели, вычисленные исходя из собственного разброса (сигма выборки), называются показателями пригодности (поскольку они описывают собственную пригодность процесса).
Использование экспериментов для повышения пригодности
Использование экспериментов для повышения пригодности
Как уже отмечалось, чем выше показатель Cp, тем лучше процесс – и это соотношение не знает верхнего предела. Вопросы цены качества, т.е. убытков, связанных с плохим качеством, подробно обсуждаются в связи с методами робастных экспериментов Тагучи (см.
раздел Планирование эксперимента). Как правило, более высокое качество обычно приводит к снижению общей себестоимости. Хотя издержки производства при этом увеличиваются, но убытки, вызванные плохим качеством, например, из-за рекламаций потребителей, потери доли рынка и т.п., обычно намного превышают затраты на контроль качества. На практике два или три хорошо спланированных эксперимента, проведенных в течение нескольких недель, часто позволяют достичь значения показателя Cp, равного 5 или выше. Если вы не знакомы с планированием экспериментов, но интересуетесь качеством процесса, настоятельно рекомендуем ознакомиться с обзором методов, подробно описанных в главе Планирование эксперимента.
Проверка предположения о нормальности распределения
Проверка предположения о нормальности распределения
Только что рассмотренные показатели имеют смысл только тогда, когда измеряемые параметры качества действительно подчиняются нормальному распределению (показатели пригодности для распределений, отличных от нормального, будут введены ниже). Существуют специальные критерии для проверки предположения о нормальности (например, критерий Колмогорова-Смирнова или критерий хи-квадрат), которые описаны в большинстве учебников по статистике и подробно обсуждаются в разделе Непараметрическая статистика и подгонка распределений .
Визуальная проверка на нормальность проводится с помощью графиков вероятность-вероятность (В-В) и квантиль-квантиль (К-К) для нормального распределения. Ниже, после обсуждения показателей пригодности для распределений, отличных от нормального, эти графики будут рассмотрены более подробно.
Доверительные границы
Доверительные границы
До введения в начале 80-тых годов показателей пригодности общим методом описания характеристик производственного процесса был расчет и изучение границ доверительного интервала этого процесса (см., например, Hald, 1952). Смысл этой процедуры таков. Сначала предположим, что соответствующий параметр качества нормально распределен на совокупности выпускаемых изделий; тогда можно подсчитать верхнюю и нижнюю границы интервала, гарантирующие с определенным доверительным уровнем (вероятностью), что определенный процент совокупности находится в этих пределах.
Другими словами, если заданы:
- конкретный объем выборки (n),
- среднее процесса,
- стандартное отклонение (сигма),
- доверительный уровень и
- процент совокупности, который должен попасть в интервал,
См. также раздел Негауссовские распределения.
| Оглавление |
Повторяемость и воспроизводимость измерений
- Введение
- Методы вычислений
- Графики повторяемости и воспроизводимости
- Компоненты дисперсии
- Выводы
Введение
Анализ повторяемости и воспроизводимости связан с изучением вопроса о точности измерений. Цель анализа повторяемости и воспроизводимости – определить, какая часть изменчивости результатов измерений вызвана (1) различием измеряемых изделий или деталей (изменчивость деталей), (2) различием операторов или приборов, осуществляющих измерения, (воспроизводимость) и (3) ошибками (погрешностями) измерений, осуществляемых теми же операторами при нескольких измерениях одинаковыми приборами одних и тех же деталей (повторяемость). В идеальном случае все колебания результатов измерений вызваны изменчивостью самих деталей, и лишь пренебрежимо малая часть зависит от воспроизводимости (приборов и операторов) и повторяемости (повторных измерений).
Если вернуться к примеру с поршневыми кольцами, то для обнаружения отклонения диаметров от номинального на 0.01 мм потребуются измерительные приборы (калибры) соответствующей точности. Описываемые далее процедуры позволяют инженеру вычислить необходимую точность инструментов и разных операторов, использующих их, в сравнении с разбросом параметров деталей внутри выборки.
Стандартные показатели повторяемости, воспроизводимости и изменчивости деталей можно вычислить на основе размахов (как это все еще принято в таких экспериментах) или с помощью анализа таблицы дисперсий (ДА) (как, например, рекомендуется в ASQC/AIAG, 1990, стр. 65).
Кроме того, таблица дисперсионного анализа содержит F-тест (проверку статистической значимости) взаимодействия оператор-деталь и выдает оценки дисперсий, стандартных отклонений и доверительных интервалов для компонент модели дисперсионного анализа.
Наконец, можно рассчитать соответствующие проценты полной изменчивости и получить так называемую статистику допустимости. Дополнительную информацию можно найти в Duncan (1974), Montgomery (1991) и в DataMyte Handbook (1992); иллюстрированные инструкции с примерами представлены в публикациях ASQC/AIAG Measurement systems analysis reference manual (1990) и Fundamental statistical process control reference manual (1991).
Обратите внимание, что существуют и другие процедуры для анализа различных типов планов, которые подробно описаны, например, в разделе Методы дисперсионного анализа. Методы, описанные в разделе Компоненты дисперсии и смешанные модели дисперсионного анализа, целесообразно использовать для анализа очень больших вложенных планов (которые имеют более 200 уровней) или иерархических вложенных планов (со случайными эффектами или без них).
Методы вычислений
Методы вычислений
Каждое измерение можно считать состоящим из компонент, связанных:
- с характеристиками измеряемой детали или изделия,
- с надежностью измерительного прибора,
- с особенностями оператора (человека, применяющего измерительный прибор).
Тогда можно вычислить соответствующие компоненты дисперсии, чтобы оценить повторяемость (дисперсию, связанную с различиями результатов повторных испытаний), воспроизводимость (дисперсию, связанную с различиями между операторами), и изменчивость деталей (дисперсию, связанную с различиями между деталями). Если вы не знакомы с основной идеей дисперсионного анализа, рекомендуем вам прочитать соответствующий раздел. Описанные там методы можно использовать в том числе и для процедур анализа повторяемости и воспроизводимости.
Графики повторяемости и воспроизводимости
Графики повторяемости и воспроизводимости
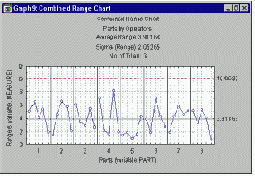
Существует несколько способов графически представить результаты экспериментального исследования повторяемости и воспроизводимости. Предположим, что вы производите небольшие сушильные шкафы (печи), применяемые для сушки материалов, используемых в других производственных процессах. Эти печи должны работать при номинальной температуре около 100 градусов Цельсия. В данном исследовании 5 разных инженеров (операторов) трижды (три опыта) измерили одну и ту же выборку из 8 печей (деталей). Можно построить график средних значений измерения каждой из 8 деталей каждым оператором. Если измерительная система воспроизводима, то характер изменения средних по трем опытам от детали к детали должен быть сходным для всех 5 инженеров, принявших участие в исследовании.
R и S карты.
R и S карты.
В разделе Контроль качества подробно обсуждается концепция R(размах) и S(сигма) карт для контроля за изменчивостью процесса. Можно применить эти концепции в данной ситуации и построить график размахов (или сигм) для операторов и деталей; эти графики позволят выявить сильные отклонения (выбросы) среди операторов и деталей. Если какой-нибудь оператор дает особенно большой разброс измерений, вам захочется выяснить, почему именно у него возникли трудности с получением надежных результатов (например, возможно, он неправильно понял инструкции по использованию измерительного прибора).
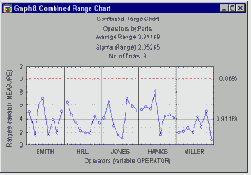
Аналогичным образом, R карта для деталей позволяет выявить детали, для которых особенно трудно получить надежные измерения; исследование этой конкретной детали может помочь понять недостатки применяемой измерительной системы.
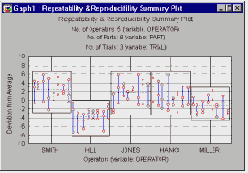
Итоговый график повторяемости и воспроизводимости.
Итоговый график повторяемости и воспроизводимости.
На итоговом графике показаны индивидуальные измерения, сделанные каждым инженером (оператором). Измерения представлены отклонениями от соответствующих средних значений для соответствующей детали. Каждое измерение показано на графике в виде точки, а результаты опытов, проведенных для каждой детали конкретным оператором, соединены вертикальными линиями. Точки, представляющие сделанные каждым инженером измерения, заключены в прямоугольник ("ящик"), показывающий общий разброс измерений, сделанных соответствующим оператором (см. следующий рисунок).
Компоненты дисперсии (см. также раздел Компоненты дисперсии)
Компоненты дисперсии (см. также раздел Компоненты дисперсии)
Доля изменчивости и процент допуска.
Доля изменчивости и процент допуска.
Величина процента допуска позволяет оценить качество измерительной системы по отношению к общей изменчивости процесса и соответствующему размаху допуска. При этом можно задать диапазон допуска и число сигма-интервалов. Параметр Число сигма-интервалов будет использован для расчета соответствующей величины изменчивости, обусловленной повторяемостью, воспроизводимостью, изменчивостью деталей и т.п. Как правило, число сигма-интервалов берется равным 5.15. В этот диапазон попадает 99% площади под кривой номального распределения. Это означает, что такой интервал будет включать 99% всех значений с соответствующими характеристиками изменчивости.
Процент от общей изменчивости.
Процент от общей изменчивости.
Эта величина характеризует долю изменчивости, обусловленную различными источниками (компонентами), по отношению к общей изменчивости (размаху) измерений.
Анализ дисперсии.
Анализ дисперсии.
Помимо вычислений оценок компонент дисперсии по размахам, существует более точный метод, основанный на дисперсионном анализе (см. Duncan, 1974, ASQC/AIAG, 1990 ).
Можно рассматривать три фактора R & R эксперимента (Операторы, Детали, Опыты) как случайные факторы в трехфакторной модели дисперсионного анализа.
Подробную информацию о традиционно рассматриваемых моделях можно найти в публикации ASQC/AIAG (1990, стр. 92-95) или в работе Duncan (1974, стр. 716-734). Обычно взаимодействия фактора испытаний (опытов) со всеми другими факторами считают несущественными. Это разумно, поскольку трудно представить, как могут возникать систематические ошибки измерения некоторых деталей при повторных опытах, особенно если порядок деталей и опытов случаен.
В отличие от этого взаимодействие Операторы-Детали может быть существенным. Так, естественно ожидать, что некоторые менее опытные операторы будут склонны к каким-то специфическим ошибкам, что приведет к систематическим искажениям при измерении определенных деталей. Поэтому можно ожидать, что эти факторы взаимодействуют (см. описание терминов дисперсионного анализа в соответствующем разделе).
В том случае, когда парные взаимодействия статистически значимы, можно отдельно оценить компоненты дисперсии, порожденные различиями операторов и связанные с взаимодействием операторов и деталей. При наличии значимого взаимодействия суммарная изменчивость, связанная с повторяемостью и воспроизводимостью, определяется как сумма трех компонент: повторяемости (ошибок измерения), ошибок оператора и ошибок оператора по данной детали.
Если взаимодействие операторов и деталей не является статистически значимым, можно пользоваться более простой аддитивной моделью без взаимодействий.
Выводы
Выводы
Итак, цель изучения повторяемости и воспроизводимости – позволить инженеру, отвечающему за контроль качества, оценить точность используемой в процессе измерительной системы. Очевидно, что измерительная система с плохой повторяемостью (большим разбросом между опытами) или воспроизводимостью (большим разбросом для разных операторов) по сравнению с разбросом при измерении разных деталей не пригодна для контроля качества. Например, полученные с ее помощью результаты нельзя использовать при построении карт контроля качества и в процедурах оценки пригодности и выборочного контроля при анализе производственных процессов.
| Оглавление |
Негауссовские распределения
- Введение
- Подгонка распределений методом моментов
- Качество подгонки: графики квантилей и вероятностей
- Негауссовские индексы пригодности (метод процентилей)
Введение
Основное назначение.
Основное назначение.
Концепция анализа пригодности подробно рассматривается в разделе Анализ пригодности. Анализируя качество процесса (например, производственного), полезно оценить долю изделий, выходящих за границы заранее заданного диапазона допустимых значений (допуска). Например, так называемый показатель Cp вычисляется по формуле:
Cp = (ВГД - НГД)/(6*сигма)
где сигма – это оценка стандартного отклонения процесса, а ВГД и НГД – это верхняя и нижняя границы допуска соответственно. Если распределение соответствующего параметра качества или переменной (например, диаметров поршневых колец) нормальное и процесс идеально центрирован (т.e. среднее процесса равно номиналу), то этот показатель можно интерпретировать как долю стандартной кривой нормального распределения (ширины процесса), попадающую в предписанные техническими условиями границы. Если процесс не центрирован, используется скорректированный показатель Cpk.
Негауссовские распределения.
Негауссовские распределения.
Наблюдаемую гистограмму можно аппроксимировать отличным от нормального распределением и вычислить показатели пригодности с помощью так называемого метода процентилей. Помимо конкретных распределений можно использовать для расчета показателей пригодности два общих семейства распределений – Джонсона (Johnson, 1965; см. также Hahn and Shapiro, 1967) и Пирсона (Johnson, Nixon, Amos, and Pearson, 1963; Gruska, Mirkhani, and Lamberson, 1989; Pearson and Hartley, 1972), которые позволяют аппроксимировать широкий спектр непрерывных распределений. Для всех распределений можно также вычислить таблицы ожидаемых частот, ожидаемое число наблюдений, выходящих за рамки технических условий, и построить графики квантиль-квантиль (К-К) и вероятность-вероятность (В-В) (см.
ниже). Конкретный метод вычисления показателей пригодности процесса на основе этих распределений описан в работе Clements (1989).
Графики квантиль-квантиль и вероятность-вероятность.
Графики квантиль-квантиль и вероятность-вероятность.
Существуют различные методы оценки качества подгонки к наблюдаемым данным. Кроме таблицы наблюдаемых и ожидаемых частот для разных интервалов и критериев качества подгонки Колмогорова-Смирнова и хи-квадрат, можно построить графики квантилей и вероятностей для всех распределений. Эти диаграммы рассеяния строятся таким образом, что если распределение наблюдаемых значений соответствует теоретическому, то точки наблюдений ложатся на графике на прямую линию.
Подгонка распределений методом моментов
Подгонка распределений методом моментов
Кроме некоторых конкретных типов распределений можно использовать для аппроксимации распределения из общих "семейств" – так называемые кривые Джонсона и Пирсона, имеющие те же первые четыре момента, что и наблюдаемое распределение.
Общий подход.
Общий подход.
Форму большинства непрерывных распределений в ряде случаев можно достаточно полно охарактеризовать первыми четырьмя моментами. Если аппроксимировать гистограмму наблюдений распределением, имеющим то же среднее (первый момент), дисперсию (второй момент), асимметрию (третий момент) и эксцесс (четвертый момент), то общая форма полученной кривой может достаточно хорошо соответствовать наблюдаемому распределению. Далее по этой кривой можно вычислить процентили и оценить долю изделий, которые удовлетворяют техническим условиям.
Кривые Джонсона.
Кривые Джонсона.
В 1949 году Джонсон описал систему плотностей вероятности, представляющих собой преобразования стандартной кривой нормального распределения (см. подробности в Hahn and Shapiro, 1967). Применением этих преобразований к стандартной нормальной величине можно аппроксимировать различные, отличные от нормального распределения, включая распределения, сосредоточенные на интервалах и полуинтервалах (например, U-образные).
Преимущество этого подхода в том, что после подгонки конкретной кривой Джонсона для вычисления ожидаемых значений процентных точек этой кривой можно использовать нормальную функцию распределения. Методы подгонки кривых Джонсона по первым четырем моментам эмпирического распределения подробно описаны в Hahn and Shapiro, 1967, стр. 199-220; и в Hill, Hill, and Holder, 1976.
Кривые Пирсона.
Кривые Пирсона.
Другая система плотностей предложена Карлом Пирсоном (см. например, Hahn and Shapiro, 1967, стр. 220-224). Эта система состоит из семи решений дифференциального уравнения (из 12, первоначально перечисленных Пирсоном), которые тоже аппроксимируют широкое разнообразие кривых разной формы. Gruska, Mirkhani, and Lamberson (1989) подробно описали, как подогнать к данным различные кривые Пирсона. Метод вычисления конкретных процентилей кривых Пирсона также описан в работе Davis and Stephens (1983).
Качество подгонки: графики вероятностей и квантилей
Качество подгонки: графики вероятностей и квантилей
Для каждого распределения можно вычислить таблицу ожидаемых и наблюдаемых частот и значения критерия хи-квадрат, а также d-критерия Колмогорова-Смирнова. Тем не менее, сначала лучше использовать визуальные методы оценки качества подгонки. Для этого применяются два стандартных графика: квантиль-квантиль и вероятность-вероятность.
Графики квантиль-квантиль.
Графики квантиль-квантиль.
На графиках квантиль-квантиль (кратко, К-К) наблюдаемые значения переменной откладываются напротив теоретических квантилей. Чтобы построить К-К график, n наблюдаемых значений упорядочиваются в порядке возрастания (строится вариационный ряд наблюдений):
x1



По одной оси графика откладываются полученные порядковые статистики, а по другой значения:
F-1 ((i-radj)/(n+nadj))
где i – ранг соответствующего наблюдения, radj и nadj – поправки (

Заметим, что кроме величины обратной функции распределения, на противоположной оси графика можно отложить функцию распределения, т.е. не только нормированные значения теоретического распределения, но и соответствующие значения вероятности.
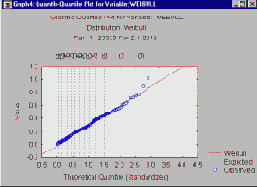
Хорошее соответствие теоретического распределения наблюдаемым значениям проявится на этом графике, если нанесенные на него точки расположатся вдоль прямой линии. Заметим, что поправки radj и nadj обеспечивают попадание аргумента для обратной функции распределения, в интервал между 0 и 1, но не включая 0 и 1 (см. Chambers, Cleveland, Kleiner, and Tukey, 1983).
Графики вероятность-вероятность.
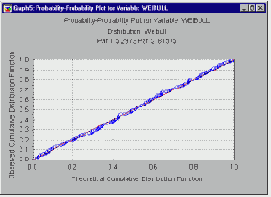
Графики вероятность-вероятность.
На графиках вероятность-вероятность (кратко В-В) наблюдаемая функция распределения откладывается на одной оси, а теоретическая функция распределения – на другой. Как и для графиков К-К, значения соответствующей переменной сначала упорядочиваются в порядке возрастания. Наблюдение с номером i откладывается по одной оси как i/n (т.е. наблюдаемая функция распределения), а по другой оси как F(x(i)), где F(x(i)) обозначает величину теоретической функции распределения для соответствующего наблюдения x(i). Если теоретическая функция распределения хорошо аппроксимирует наблюдаемое распределение, то все точки на этом графике должны попасть на диагональную линию (как на показанном ниже рисунке).
Негауссовские индексы пригодности (метод процентилей)
Негауссовские индексы пригодности (метод процентилей)
Как уже отмечалось ранее, показатели пригодности в общем случае вычисляются для того, чтобы оценить качество процесса, т.е. чтобы получить оценки разброса производимых изделий (размах процесса) по отношению к размаху допуска. Для стандартных показателей пригодности процесса, основанных на нормальном распределении, размах процесса обычно определяется как 6 сигма, т.е. как плюс-минус утроенная оценка стандартного отклонения процесса. Для стандартной кривой нормального распределения эти границы (zl = -3 и zu = +3) пересчитываются в 0.135 и 99.865 процентили соответственно.
Для распределений, отличных от нормального, границы 3 сигма, а также среднее (zM = 0.0) можно заменить соответствующими стандартными значениями, дающими те же величины процентилей под кривой негауссовского распределения. Эта процедура подробно описана в работе Clements (1989).
Индексы (показатели) пригодности.
Индексы (показатели) пригодности.
Ниже приведены формулы для вычисления негауссовских показателей пригодности:
Cp = (ВГД-НГД)/(Up-Lp)
CpL = (M-НГД)/(M-Lp)
CpU = (ВГД-M)/(Up-M)
Cpk = Min(CpU, CpL)
В этих уравнениях M обозначает медиану (50 процентиль) соответствующего распределения, а Up и Lp – 99.865 и 0.135 процентили соответственно, в случае если вычисления основываются на размахе процесса, равном ±3 сигма. Обратите внимание, что значения Up и Lp могут быть другими, если размах процесса задан другими границами (например, ±2 сигма).
| Оглавление |
Анализ Вейбулла, надежность и времена отказов
- Основные задачи
- Распределение Вейбулла
- Цензурированные наблюдения
- Двух- и трехпараметрическое распределение Вейбулла
- Оценка параметров
- Критерии согласия
- Интерпретация результатов
- Группированные данные
- Изменения порядка времен отказов для многократно цензурированных данных
- Функция распределения Вейбулла, надежность и функции риска
Анализ Вейбулла, надежность и времена отказов
Основные задачи
Основные задачи
Надежность устройства или образца продукции является важным показателем качества. Особенный интерес представляет количественная оценка надежности, позволяющая оценить ожидаемое время жизни или, в инженерных терминах, время безотказной работы прибора. Предположим, вы летите на маленьком самолете с одним двигателем. Тогда для вас жизненно важно знать вероятность отказа двигателя на различных этапах его эксплуатации (например, после 500 часов работы , после 1000 часов и т.д.) Имея хорошую оценку надежности двигателя и доверительный интервал, можно принять рациональное решение о том, когда следует заменить двигатель или отправить его на капитальный ремонт.
Распределение Вейбулла
Распределение Вейбулла
Для описания времен отказов образцов, поставленных на испытание, традиционно используется распределение Вейбулла (см. также раздел Распределение Вейбулла, функция надежности и функция риска), названное в честь шведского исследователя Валоди Вейбулла (Waloddi Weibull), применявшего его для описания времен отказов разного типа; в России исследование этого распределения связано с именем известного русского математика Б.В. Гнеденко, бывшего долгие годы профессором Московского Университета, и часто называется распределением Вейбулла-Гнеденко (см. также Hahn and Shapiro, 1967; распределение Вейбулла-Гнеденко использовалось для описания времен жизни электронных устройств, ламп, подшипников и даже некоторых финансовых задач). Функция интенсивности и U-образная кривая.
Функция интенсивности и U-образная кривая.
Часто при проведении анализа надежности естественно рассматривать вероятность отказа в течение малого интервала времени при условии, что в начале интервала отказа не произошло. Такая функция называется функцией риска или функцией интенсивности отказов и формально определяется следующим образом:
h(t) = f(t)/(1-F(t))
где h(t) обозначает функцию интенсивности отказов или функцию риска в момент t, f(t)- плотность, а F(t) - функцию распределения времен отказов.
Для большинства исследуемых изделий (компонент, устройств и т.д.) функция интенсивности имеет форму U- образной кривой: на ранней стадии жизни изделия риск его выхода из строя (отказ) достаточно велик (так называемая детская смертность), далее интенсивность отказов уменьшается до определенного предела, а затем вновь увеличивается из-за старения (износа) изделия до тех пор, пока все детали не выйдут из строя.
Например, автомобили в начале эксплуатации часто имеют несколько мелких дефектов, приводящих к поломке. После того как автомобиль прошел обкатку, риск его выхода из строя существенно уменьшается. Затем интенсивность отказов (поломок) возрастает, достигая в конце концов своего максимального значения (обычно после 20 лет эксплуатации или 250000 миль пробега практически всякий автомобиль выходит из строя). Типичная U-образная функция интенсивности или функция риска выглядит следующим образом:
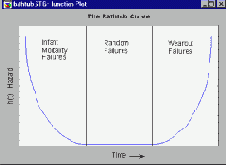
Распределение Вейбулла позволяет гибко моделировать различные возникающие на практике формы функции интенсивности. Задавая разные параметры распределения, можно получить практически любые функции риска. Ниже показаны функции интенсивности для параметров c=.5, c=1, c=2 и c=5.
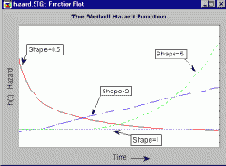
Ясно, что начальная фаза кривой аппроксимируется распределением Вейбулла с параметром формы c<1, постоянная фаза имеет параметр формы c=1, а финальная фаза (старение или износ) моделируется распределением с параметром формы c>1.
Функция распределения и функция надежности.
Функция распределения и функция надежности.
После того как оценены параметры распределения Вейбулла, можно оценить различные характеристики надежности. В частности, вычислить функцию распределения отказов (обычно обозначаемую как F(t)). Затем вы можете определить процентили функции выживаемости или функции надежности, например, оценить момент времени, когда откажет заданная доля тестируемых объектов.
Функция надежности (обычно обозначаемая как R(t)) определяется равенством R(t)=1-F(t)); иногда она называется также функцией выживания (т.к.
описывает вероятность того, что отказ произойдет после определенного момента времени t; см. например, Lee, 1992). Ниже показаны функции надежности для распределения Вейбулла, имеющие различные параметры формы.
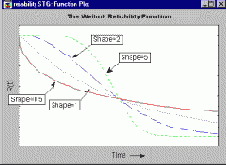
Если параметры формы меньше 1, то функция надежности резко уменьшается в начале времени жизни, затем уменьшение происходит более медленно. Если параметр формы больше 1, то сначала наблюдается небольшое уменьшение надежности, а затем, начиная с некоторой точки, она довольно быстро снижается. Точка, где все кривые пересекаются, называется характеристическим временем жизни и определяет момент, когда отказало 63.2% выборки (R(t) = 1-0.632 = .368). Эта точка равна соответствующему параметру масштаба b двухпараметрического распределения Вейбулла с параметром


Формулы для вычисления соответствующих характеристик приведены в разделе Распределение Вейбулла, надежность и функции риска.
Цензурированные наблюдения
Цензурированные наблюдения
При проведении большинства исследований надежности не все наблюдения завершаются отказами. Как правило, на завершающем этапе исследования становится ясно, что определенное количество объектов не отказало и точные времена их жизни неизвестны. Такие наблюдения называются цензурированными наблюдениями. Идея цензурирования и методы анализа цензурированных данных подробно описаны в разделе Анализ выживаемости. Заметим, что цензурирование может осуществляться очень разными способами, т.к. имеется много различных методов проверки надежности.
Цензурирование типа I и типа II.
Цензурирование типа I и типа II.
Так называемое цензурирование типа I применяется в ситуации, когда заранее фиксируется время проведения наблюдений (мы берем 100 ламп и оканчиваем эксперимент спустя некоторое промежуток времени, например, через 120 часов после начала). В этом случае интервал времени зафиксирован и число отказавших (перегоревших) ламп представляет собой случайную величину. При цензурировании типа II заранее задается доля (процент) отказов, но время наблюдения не фиксируется (например, мы проводим эксперимент пока не перегорят 50% ламп).
Очевидно при данном подходе мы имеем фиксированное число отказов, а время, в течение которого проводится эксперимент, является случайной величиной.
Левое и правое цензурирование.
Левое и правое цензурирование.
Дополнительно можно регулировать такой параметр, как направление цензурирования. В предыдущем примере цензурирование происходит всегда в правом направлении по временной оси (правое цензурирование), потому что исследователь точно фиксирует начало эксперимента и знает, что не отказавшие лампы будут действовать еще некоторое время после окончания эксперимента. Другой вариант возникает, когда исследователю не известно начало времени жизни объекта, например, врачу известен момент поступления пациента в госпиталь с данным диагнозом, но врач не знает, когда данный диагноз был поставлен и тем более не знает, когда болезнь началась. Такое цензурирование называется левым. Конечно, если тестируются старые лампы, то это тоже пример левого цензурирования, т.к. не известен момент начала их эксплуатации.
Однократное и многократное цензурирование.
Однократное и многократное цензурирование.
Наконец, возможны ситуации в которых цензурирование происходит в различные моменты времени (многократное цензурирование), или только в один момент времени (однократное цензурирование). Возвращаясь к эксперименту с электрическими лампами, заметим, что если эксперимент заканчивается в определенный момент времени, то мы имеем однократное цензурирование. Однако в медико-биологических исследованиях часто имеют дело с многократным цензурированием, например, продолжительность лечения и момент выписки могут быть разными для разных пациентов, и в то же время после выписки исследователь точно знает, что пациенты пережили все этапы лечебной процедуры.
Рассматриваемые методы применимы прежде всего к правому цензурированию, а также к однократно или многократно цензурированным данным.
Двух- и трехпараметрическое распределение Вейбулла
Двух- и трехпараметрическое распределение Вейбулла
Распределение Вейбулла ограничено с левой стороны.
Если вы посмотрите на график плотности распределения, то увидите, что значение x-



Оценка параметров
Оценки максимального правдоподобия.
Оценки максимального правдоподобия.
Для получения оценок максимального правдоподобия параметров двух- или трехпараметрического распределения Вейбулла используются стандартные итерационные методы минимизации функций. Особенности этих методов оценивания изложены в книге Dodson (1994); подробное описание итерационного метода Ньютона-Рафсона для численного построения оценок максимального правдоподобия можно найти в книге Keats and Lawrence (1997).
Оценка параметра положения для трехпараметрического распределения Вейбулла связана с рядом вычислительных трудностей (см., например, Lawless, 1982). В частности, если параметр формы меньше 1, то не существует оценок максимального правдоподобия параметров. В других случаях функция правдоподобия может иметь несколько локальных максимумов. В последнем случае Лоулесс (Lawless) рекомендует использовать для оценки параметра положения наименьшее время отказа (или значение чуть меньшее его).
Вероятностные графики, основанные на рангах.
Вероятностные графики, основанные на рангах.
Независимо от типа распределения можно оценить функцию распределения, используя:
Медианный (серединный) ранг:
F(t) = (j-0.3)/(n+0.4)
Cредний ранг:
F(t) = j/(n+1)
Параметр Уайта:
F(t) = (j-3/8)/(n+1/4)
где j обозначает порядок отказов или ранг до момента t (для многократного цензурирования вычисляются взвешенные порядковые моменты отказа, см. Dodson, p. 21), n – общее число наблюдений. Таким образом, можно построить следующий график.

Заметим, что горизонтальная ось графика имеет логарифмический масштаб; по вертикальной оси отложен log(log(100/(100-F(t))) (вероятностная шкала показана на левой оси y). График позволяет оценить два параметра распределения Вейбулла; в частности, параметр формы равен угловому коэффициенту (slope) прямой линии, а параметр масштаба оценивается как exp(-intercept/slope).
Оценка параметра положения по вероятностным графикам.
Оценка параметра положения по вероятностным графикам.
Представленный выше график показывает, что регрессионная прямая обеспечивает хорошую подгонку к данным. Если параметр положения определен неверно (например, не равен 0), то линейная подгонка оказывается значительно хуже. Поэтому имеет смысл построить вероятностные графики для нескольких значений параметра положения, как показано на следующей иллюстрации.
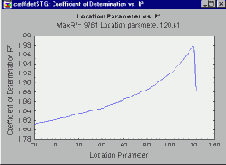
На приведенном выше рисунке, построенном на основе данных из работы Dodson (1994, Table 2.9), показан коэффициент детерминации R-квадрат (квадрат множественного коэффициента корреляции), который обычно используется для оценки качества линейной подгонки на вероятностном графике. При этом на оси x отложены различные значения параметра положения. Такой график часто бывает полезен, когда процедуры построения оценок максимального правдоподобия для трехпараметрического распределения Вейбулла не дают желаемого результата. С его помощью можно понять, существует ли единственное оптимальное значение параметра положения (как на показанном выше графике) или мы имеем дело с несколькими локальными максимумами.
График функции риска или интенсивности отказов.
График функции риска или интенсивности отказов.
Другой метод оценивания параметров двухпараметрического распределения Вейбулла – графический анализ функции интенсивности (как обсуждалось выше, функция интенсивности или, как ее часто называют, функция риска равняется вероятности наступления отказа в малый интервал времени [t, t + dt) при условии что до момента t отказ не произошел). Этот графический метод аналогичен методу оценки параметров из вероятностного графика функции надежности. Вначале строится график кумулятивной функции интенсивности (по оси х откладываются логарифмы времен жизни); тогда подогнанная регрессионная прямая дает наглядное представление о параметрах распределения. Как и в вероятностных графиках параметр формы оценивается через угол наклона регрессионной прямой, а параметр масштаба может быть оценен как exp(-св.член/коэф.наклона). Подробности можно найти в работе Dodson (1994), а некоторые формулы - в разделе Распределение Вейбулла, надежность и функция риска.
Метод моментов.
Метод моментов.
Идея этого метода, широко обсуждаемого в литературе, состоит в том, чтобы вначале оценить моменты распределения Вейбулла, приравнять их к теоретическим моментам, а затем из полученных уравнений найти параметры распределения. Фактически этот метод используется для подгонки кривых Джонсона для негауссовских распределений с целью последующего вычисления индексов пригодности (см. раздел Подгонка распределений методом моментов). Однако этот метод не подходит для обработки цензурированных наблюдений и, следовательно, для анализа времен отказов.
Сравнение методов оценивания.
Сравнение методов оценивания.
Додсон (Dodson, 1994) приводит результаты моделирования методом Монте-Карло и сравнивает различные способы оценивания. Как правило, оценки максимального правдоподобия являются лучшими для больших выборок (например, n>15), тогда как графические методы более точны для малых выборок.
Замечание об осторожном использовании доверительных интервалов, построенных методом максимального правдоподобия.
Замечание об осторожном использовании доверительных интервалов, построенных методом максимального правдоподобия.
Система STATISTICA вычисляет доверительные интервалы оценок максимального правдоподобия функции надежности, основываясь на стандартных ошибках. Додсон (Dodson, 1994) советует с осторожностью подходить к доверительным интервалам, полученным из оценок максимального правдоподобия или, более точно, оценок, при вычислении которых используется информационная матрица. Если параметр формы меньше 2, дисперсия таких оценок теряет точность и предпочтительнее использовать графические методы, основанные на непараметрических доверительных интервалах.
Критерии согласия
Критерии согласия
Имеется несколько критериев оценки качества подгонки распределения Вейбулла к данным, которые всесторонне рассматриваются в работе Lawless (1982). Мы лишь кратко перечислим эти критерии.
Критерий Холлендера-Прошана.
Критерий Холлендера-Прошана.
Этот критерий сравнивает теоретическую функцию надежности с оценкой Каплана-Майера. Точные формулы вычисления достаточно сложны и могут быть найдены в книге Dodson (1994, глава 4). Критерий Холлендера-Прошана применяется к полным, однократно или многократно цензурированным данным; однако Додсон (Dodson, 1994) отмечает слабую мощность этого критерия, например, для сильно цензурированных данных. Можно проверить нормальность распределения C статистики Холлендера-Прошана.
Критерий Манна-Шойера-Фертига.
Критерий Манна-Шойера-Фертига.
Этот критерий был предложен Манном, Шойером и Фертигом в 1973 году и описан в работах Dodson (1994) и Lawless (1982). Нулевая гипотеза предполагает, что данные имеют распределение Вейбулла с оцененными параметрами. Нельсон (Nelson, 1982) отмечает хорошую мощность этого критерия и применимость к данным с цензурированием типа II. Вычислительные детали приводятся в работах Dodson (1994) и Lawless (1982); критические значения для этой статистики вычислены методом Монте-Карло и табулированы для n (объем выборки) от 3 до 25.
Критерий Андерсона-Дарлинга.
Критерий Андерсона-Дарлинга.
Критерий Андерсона-Дарлинга позволяет сравнить эмпирическую и теоретическую функцию распределения, однако применяется он только к полным наблюдениям (без цензурирования). Критические значения статистики Андерсона-Дарлинга табулированы (см., например, Dodson, 1994, Table 4.4) для размеров выборки от 10 до 40.
Интерпретация результатов
Интерпретация результатов
При удовлетворительных результатах подгонки распределения Вейбулла к распределению времен отказов можно использовать различные графики и таблицы для исследования надежности исследуемых образцов. Если же не удалось получить хорошую подгонку распределения Вейбулла к наблюдаемым данным, то для определения формы функции надежности можно использовать независимые от распределения методы оценки параметров.
Графики функции надежности.
Графики функции надежности.
На этом графике показаны оценки функции надежности вместе с соответствующими доверительными границами.

Заметьте, что помимо стандартных могут быть вычислены и показаны на графике также и независимые от распределения, непараметрические оценки.
Графики функции риска (интенсивности отказов).
Графики функции риска (интенсивности отказов).
Как уже отмечалось, функция интенсивности или функция риска (мы используем и тот, и другой термин) описывает вероятность отказа (смерти) в малый интервал времени при условии, что в начале интервала отказа не было. График функции риска дает информацию об условной вероятности отказов.
Процентные точки функции надежности.
Процентные точки функции надежности.
Основываясь на подогнанной функции распределения Вейбулла, можно вычислить процентили функции надежности (функции выживания) вместе с доверительными границами (для оценок максимального правдоподобия). Эти оценки особенно важны для вычисления ожидаемой доли образцов, выживших к определенному моменту времени.
Группированные данные
В некоторых случаях времена отказов представляются в виде сгруппированных данных. В частности, во многих реальных исследованиях сложно оценить время отказов с достаточной точностью, но тем не менее, можно определить сколько отказов произошло или сколько наблюдений было цензурировано в течение определенного интервала времени.
Такого рода данные, так называемые таблицы жизни (отказов) обсуждаются в разделе Анализ выживаемости. Существует два основных метода подгонки распределения Вейбулла к группированным данным.
Первый подход состоит в интерполяции, т.е. в переводе таблицы в непрерывный массив данных, при этом предполагается, (1) что каждый отказ происходит в середине интервала группировки, (2) что цензурирование происходит после отказов (иными словами, цензурированные наблюдения располагаются за отказами в каждом интервале группировки). Лоулесс (Lawless, 1982) советует пользоваться данным методом в ситуациях, когда интервалы группировки относительно малы.
В другом случае вы можете рассматривать имеющиеся данные как таблицу времен жизни и использовать для подгонки распределения Вейбулла метод взвешенных наименьших квадратов (см. Gehan and Siddiqui, 1973; Lee, 1992). В работе Lawless (1982) также описаны способы оценки параметров для группированных данных методом максимального правдоподобия.
Изменение порядка времен отказа для многократно цензурированных данных
Изменение порядка времен отказа для многократно цензурированных данных
Для многократно цензурированных данных вычисляется взвешенный ранг отказов для каждого момента, начиная с момента первого цензурирования. Затем этот новый ранг используется для вычисления медианного ранга и оценки функции распределения.
Модифицированный ранг с номером j вычисляется по формуле (см. Dodson 1994):
Oj = Op + ((n+1)-Op)/(1+c)
где:
n - общее число наблюдений,
Op - модифицированный ранг предыдущего наблюдения,
c - число оставшихся точек данных , включая текущую.
При этом медианный ранг вычисляется следующим образом:
F(t) = (Oj -0.3)/(n+0.4)
где Oj - модифицированный порядок отказов, n - полное число наблюдений.
Функция распределения Вейбулла, надежность и функции риска
Функция распределения Вейбулла, надежность и функции риска
Распределение Вейбулла определено для положительных значений параметров b, c и

Плотность распределения Вейбулла:
Плотность распределения Вейбулла:
f(x) = c/b*[(x-



Функция распределения (ФР) Вейбулла:
Функция распределения (ФР) Вейбулла:
F(x) = 1 - exp{-[(x-

Функция надежности.
Функция надежности.
Функция надежности вычисляется с помощью функции распределения Вейбулла по формуле:
R(x) = 1 - F(x)
Функция риска (интенсивности).
Функция риска (интенсивности).
Функция риска описывает вероятность отказа в течение малого промежутка времени при условии, что до этого момента отказа не произошло. На основе распределения Вейбулла получается функция риска следующего вида:
h(t) = f(t)/R(t) = [c*(x-

Кумулятивная функция риска:
Кумулятивная функция риска:
H(t) = (x-

В формулах для функции интенсивности и кумулятивной функции риска использованы те же обозначения, что и в приведенных выше выражениях для функций плотности и надежности.
| Оглавление |

(c) Copyright StatSoft, Inc., 1984-2001
STATISTICA is a trademark of StatSoft, Inc.