Учебник по промышленной статистике
Анализ соответствий
Анализ соответствий
Анализ соответствий
- Вводный обзор
- Дополнительные точки
- Многомерный анализ соответствий
- Матрица Берта
Вводный обзор
Вводный обзор
Анализ соответствий содержит описательные и разведочные методы анализа двухвходовых и многовходовых таблиц. Эти методы по своей природе похожи на методы Факторного анализа и позволяют исследовать структуру группирующих переменных, включенных в таблицу. Одной из наиболее общих разновидностей многовходовых таблиц типа являются частотные таблицы сопряженности (см., например, Основные статистики или Логлинейный анализ).
В классическом анализе соответствий частоты в таблице сопряженности стандартизуются таким образом, чтобы сумма наблюдений во всех ячейках была равна 1. Одной из целей анализа соответствий является представление содержимого таблицы относительных частот в виде расстояний между отдельными строками и/или столбцами таблицы в пространстве возможно более низкой размерности. Каким образом это достигается, лучше всего показать на простом примере, который будет рассмотрен далее. Заметим, что имеется некоторое сходство в интерпретации результатов анализа соответствий и Факторного анализа.
Для более полного описания данного метода, его вычислительных аспектов и его применения, рекомендуем классическую работу Greenacre (1984). Методы анализа соответствий впервые были разработаны во Франции Jean-Paul Benzerci в конце 1960-х - начале 1970-х годов (например, смотри Benzerci, 1973; см. также Lebart, Morineau, Tabard, 1977), однако в англо-говорящих странах они завоевали популярность сравнительно недавно (смотри, например, Carrol, Green и Schaffer, 1986; Hoffman и Franke, 1986). Заметим, что похожие методы независимо разрабатывались во многих странах и были известны под названиями: оптимальное шкалирование, взаимное усреднение, оптимальная оцифровка, квантификационный метод или анализ однородности. В последующих разделах будет представлено общее введение в анализ соответствий.
Обзор.Обзор.
Допустим, что вы собрали данные о пристрастии к курению сотрудников некоторой компании.
Следующие данные представлены в работе Greenacre (1984, стр. 55).
Таблица 1
Таблица 1
| 4 4 25 18 10 |
2 3 10 24 6 |
3 7 12 33 7 |
2 4 4 13 2 |
11 18 51 88 25 |
| 61 | 45 | 62 | 25 | 193 |
Это простая двувходовая таблица. Можно считать, что 4 числа в каждой строке данной таблицы являются координатами 4-х мерного пространства, и значит, можно вычислить (евклидовы) расстояния между 5-ю точками (строками) этого 4-х мерного пространства. Расстояния между данными точками в 4-х мерном пространстве объединяют (агрегируют) всю информацию о сходствах между строками в том смысле, что чем меньше расстояние, тем больше сходство между категориями курящих. Теперь, предположим, что возможно найти пространство меньшей размерности для представления точек-строк, которое сохраняет всю или почти всю информацию о различиях между строками. В рассматриваемом случае вы можете представить всю информацию о сходстве между строками (в данном случае о типе работника) в виде 1, 2 или 3-мерного графика. Хотя это может и не быть практически полезным для маленьких таблиц, аналогичных рассматриваемой, можно себе представить, как сильно выиграет представление и интерпретация очень больших таблиц (в которых, например, записаны предпочтения для 10 потребительских товаров 100 групп респондентов) в результате упрощения, полученного путем применения методов анализа соответствий (например, представить упомянутые 10 потребительских товаров в двумерном пространстве).
Масса.
Масса.
Продолжая предыдущий пример двухвходовой таблицы, рассмотрим вычислительный аспект работы программы.
Во-первых, вычисляются относительные частоты для введенной таблицы, так что сумма всех элементов таблицы будет равна 1 (каждый элемент делится на 193 - общее число наблюдений). Полученная нормированная таблица показывает, как распределена единичная масса по ячейкам. В терминологии анализа соответствий, суммы по строкам и столбцам в матрице относительных частот называются массой строки и столбца, соответственно.
Инерция.
Инерция.
Термин инерция в анализе соответствий используется по аналогии с прикладной математикой, где понятие "момент инерции" определяется как интеграл элемента массы умноженной на квадрат расстояния до центра масс (смотри, например, Greenacre, 1984, стр.35). Инерция определяется как значение статистики хи-квадрат Пирсона для двухвходовой таблицы, деленное на общее количество наблюдений (193 в примере).
Инерция и профили строк и столбцов.
Инерция и профили строк и столбцов.
Если строки и столбцы таблицы полностью независимы друг от друга, то элементы таблицы могут быть воспроизведены исключительно при помощи сумм по строкам и столбцам или, в терминологии анализа соответствий, при помощи профилей строк и столбцов. В соответствие с известной формулой для вычисления статистики Хи-квадрат для двухвходовых таблиц, ожидаемые частоты таблицы, в которой столбцы и строки независимы, вычисляются перемножением соответствующих профилей столбцов и строк и делением полученного результата на общую сумму. Любое отклонение от ожидаемых величин (ожидаемых при гипотезе о полной независимости переменных по строкам и столбцам) будет давать вклад в совокупную статистику хи-квадрат. Таким образом, анализ соответствий можно рассматривать как метод декомпозиции статистики Хи-квадрат для двухвходовых таблиц (Инерция = Хи-квадрат/Число наблюдений) с целью определения пространства наименьшей размерности, позволяющего представить отклонения от ожидаемых величин. Это напоминает задачу Факторного анализа, где осуществляется декомпозиция совокупной вариации, так чтобы снижение размерности переменных приводило к наименьшим потерям в матрице ковариаций исходных переменных.
Анализ строк и столбцов.
Анализ строк и столбцов.
Разбор предыдущего примера начался с рассмотрения точек- строк таблицы. Однако не меньший интерес могут вызывать суммарные величины по столбцам, в этом случае можно представить точки-столбцы в пространстве меньшей размерности, которое удовлетворительно воспроизводит сходство (и расстояния) между относительными частотами для столбцов таблицы. В действительности возможно одновременное отображение на одном графике точек-столбцов и точек-строк, представляющее всю имеющуюся информацию, содержащуюся в двухвходовой таблице.
Просмотр результатов.
Просмотр результатов.
Теперь рассмотрим некоторые результаты для данной таблицы. Ниже показаны так называемые сингулярные значения, собственные значения, проценты объясненной инерции, кумулятивные проценты и вклады в статистику хи-квадрат каждого собственного значения.
Таблица 2
Таблица 2
| 1 2 3 |
.273421 .100086 .020337 |
.074759 .010017 .000414 |
87.75587 11.75865 .48547 |
87.7559 99.5145 100.0000 |
14.42851 1.93332 .07982 |
Заметим, что базис в евклидовом пространстве выбирается так, чтобы расстояние между точками-строками или точками-столбцами было максимальным, и новые вектора базиса (которые независимы или ортогональны друг другу) давали все меньший и меньший вклад в величину хи-квадрат (следовательно, и величину инерции). Таким образом, процедура получения базисных векторов во многом напоминает выделение главных компонент в Факторном анализе.
Обратите внимание на то, что одна размерность, в рассматриваемом примере, объясняет 87.76% инерции, а это значит, что для рассматриваемой двухвходовой таблицы значения относительных частот, которые восстанавливаются по одной размерности, дают вклад в величину статистики Хи-квадрат (и, следовательно, инерции) в размере 87.76% от первоначального.
Две размерности позволяют объяснить 99.51% значения Хи-квадрат.
Максимальная размерность.
Максимальная размерность.
Так как частоты в таблице суммируются по строкам и по столбцам, то имеется только (число столбцов - 1) независимых элементов каждой строки и (число строк - 1) независимых элементов каждого столбца (зная значения этих элементов, вы можете заполнить оставшиеся ячейки таблицы, используя значения суммарных величин по строкам и столбцам). Следовательно, количество собственных значений, которые возможно получить для двухвходовой таблицы, равно минимум числа столбцов минус 1 и числа строк минус 1. Если используется максимальная размерность, то можно полностью восстановить всю информацию, содержащуюся в таблице.
Координаты строк и столбцов.
Координаты строк и столбцов.
Рассмотрим координаты в двумерном пространстве.
Таблица 3
Таблица 3
| -.065768 .258958 -.380595 .232952 -.201089 |
.193737 .243305 .010660 -.057744 -.078911 |
Вы можете отобразить на двумерной диаграмме координаты. Напомним, что целью анализа соответствий является представление расстояний между строками и/или столбцами двухвходовой таблицы в пространстве меньшей размерности. Также заметим, что, как и в Факторном анализе, ориентация векторов базиса выбрана таким образом, что каждый новый базисный вектор "объяснял" все меньше и меньше величину статистики Хи-квадрат (или инерции). Вы, например, можете изменить знаки всех столбцов предыдущей таблицы и повернуть, таким образом, оси на 180°.
Важным преимуществом двумерного пространства является то, что точки-строки, отображаемые в виде точек, которые находятся в непосредственной близости друг от друга, близки и по относительным частотам. Если вы построили данную диаграмму, то, рассматривая расположение точек по первой оси, обратите внимание на то, что Старшие сотрудники и Секретари относительно близки по координатам.
Если же посмотреть на строки таблицы относительных частот (частоты стандартизованы так, что их сумма по каждой строке равна 100%), то сходство для данных двух групп по категориям интенсивности курения становится очевидным.
Таблица 4
Таблица 4
| 36.36 22.22 49.02 20.45 40.00 |
18.18 16.67 19.61 27.27 24.00 |
27.27 38.89 23.53 37.50 28.00 |
18.18 22.22 7.84 14.77 8.00 |
100.00 100.00 100.00 100.00 100.00 |
Очевидно, что окончательной целью анализа соответствий является теоретическая интерпретация векторов в полученном пространстве более низкой размерности. Одним из способов, который может помочь в интерпретации полученных результатов, является представление на диаграмме точек-столбцов. В следующей таблице показаны координаты точек-столбцов:
Таблица 5
Таблица 5
| -.393308 .099456 .196321 .293776 |
.030492 -.141064 -.007359 .197766 |
Можно сказать, что первая размерность дает отличие между градациями интенсивности курения, в данном случае между категориями Некурящие и все остальные. Следовательно, можно объяснить большую степень сходства между Старшими менеджерами и Секретарями, о которой уже шла речь выше, наличием в данных группах большого количества Некурящих.
Совместимость координат строк и столбцов.
Совместимость координат строк и столбцов.
Имеется возможность для отображения координат по строкам и столбцам на одной диаграмме. Однако важно помнить, что на таких диаграммах нужно интерпретировать сходства и различия между точками-строками и точками-столбцами отдельно по строкам и отдельно по столбцам, совместная интерпретация не имеет смысла.
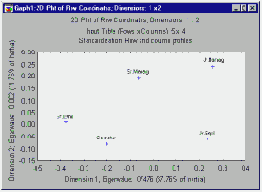
В данном примере было бы неправильно сказать, что категория Некурящие имеет сходство с категорией Старшие сотрудники (эти две точки очень близки на совместной диаграмме).
Однако, как уже отмечалось ранее, возможно делать общие замечания о природе имеющихся координат, базируясь на положении рассматриваемых точек относительно начала координат. Например, так как категория Некурящие является единственной точкой-столбцом, расположенной слева от начала координат по первой оси, и категория Старшие сотрудники также попадает туда же, то можно сказать, что первая ось отделяет категорию Некурящих от остальных, и что категория Старшие сотрудники отличается, например, от категории Младшие сотрудники тем, что в ней имеется относительно большее число некурящих сотрудников.
Шкалирование координат (возможности стандартизации).
Шкалирование координат (возможности стандартизации).
Еще одним важным решением, которое принимает аналитик, является решение о шкалировании координат. Решение о выборе той или иной опции зависит от того, собираетесь ли вы анализировать относительные проценты по рядам, по столбцам или по тем и другим одновременно. В контексте предыдущего примера, проценты по рядам сравнивались для того, чтобы проиллюстрировать наблюдаемое сходство процентов в таблице для близких точек на диаграмме. Другими словами, координаты точек прямо связаны с анализом матрицы профилей строк, в которой сумма элементов строки равна 1 (каждый элемент rij в матрице профилей строк интерпретируется как условная вероятность того, что элемент i-й строки принадлежит столбцу j). Таким образом, координаты вычисляются так, чтобы максимизировать расстояние между профилями строк (процентов по строкам). Координаты строк вычисляются по матрице профилей строк, а координаты столбцов вычисляются по матрице профилей столбцов.
Имеется также опция Канонической стандартизации (см. Gifi, 1981), эта разновидность стандартизации применяется к столбцам и строкам матрицы относительных частот. Данная стандартизация применяется для шкалирования стандартизаций профилей по строкам и столбцам и не является широко распространенной. Отметим, что существует возможность задавать собственную стандартизацию по выбору пользователя, если имеются значения собственных значений и собственных векторов.
Метрика координатной системы.
Метрика координатной системы.
Во введении термин расстояние также использовался для обозначения различий между строками и столбцами матрицы относительных частот, которые, в свою очередь, представлялись в пространстве меньшей размерности в результате использования методов анализа соответствий. В действительности, расстояния представленные в виде координат в пространстве соответствующей размерности это не просто евклидовы расстояния, вычисленные по относительным частотам столбцов и строк, а некоторые взвешенные расстояния. Процедура подбора весов устроена таким образом, чтобы в пространстве более низкой размерности метрикой являлась бы метрика Хи-квадрат, учитывая, что вы сравниваете точки-строки и выбираете стандартизацию профилей строк или стандартизацию профилей строк и столбцов или что вы сравниваете точки-столбцы и выбираете стандартизацию профилей столбцов или стандартизацию профилей строк и столбцов.
В этом случае (но не в случае канонической стандартизации) возведенное в квадрат евклидово расстояние между, например, двумя точками-строками i и i' в некоторой координатной системе соответствующей размерности аппроксимируют взвешенное (например, Хи-квадрат) расстояние между относительными частотами (см. Hoffman и Franke, формула 21):
dii '2 =

В данной формуле dii '2 - квадрат расстояния между двумя точками, cj - сумма по всем элементам в столбце j стандартизованной частотной таблицы (в которой сумма по всем элементам или масса равна 1), pij - элемент стандартизованной частотной таблицы (строка i, столбец j), ri - сумма по всем элементам в строке i таблицы относительных частот, оператор

Оценка качества решения.
Оценка качества решения.
Имеется также некоторые дополнительные статистики, помогающие интерпретировать качество найденного решения.
Все ( или большинство) точки должны быть правильно представлены, т.е. расстояния между ними в результате применения процедуры анализа соответствий не должны искажаться. В следующей таблице представлены результаты вычисления статистик по имеющимся координатам строк, основанные только на одномерном решении в предыдущем примере (т.е. только одно измерение использовалось для восстановления профилей строк матрицы относительных частот).
Таблица 6
Таблица 6
| -.065768 .258958 -.380595 .232952 -.201089 |
.056995 .093264 .264249 .455959 .129534 |
.092232 .526400 .999033 .941934 .865346 |
.031376 .139467 .449750 .308354 .071053 |
.003298 .083659 .512006 .330974 .070064 |
.092232 .526400 .999033 .941934 .865346 |
Координаты.
Координаты.
Первый столбец данной таблицы результатов содержит координаты, интерпретация которых, как мы уже отмечали, зависит от выбранной стандартизации. Размерность выбирается пользователем (в данном примере мы выбрали одномерное пространство), и координаты отображаются для каждого измерения (т.е. отображается по одному столбцу координат на каждую ось).
Масса.
Масса.
Столбец Масса содержит суммы всех элементов для каждой строки матрицы относительных частот (т.е. для матрицы, где каждый элемент содержит соответствующую массу, как уже упоминалось выше). Напомним, координаты вычисляются на основе матрицы условных вероятностей, представленной в столбце Масса.
Качество.
Качество.
Столбец Качество содержит информацию о качестве представления соответствующей точки-строки в координатной системе, определяемой выбранной размерностью. В рассматриваемой таблице было выбрано только одно измерение, поэтому числа в столбце качество являются качеством представления результатов в одномерном пространстве.
Повторим еще раз, что в вычислительном плане целью анализа соответствий является представление расстояний между точками в пространстве более низкой размерности. Если вы используете максимальную размерность (равную минимуму числа строк и столбцов минус один), то вы можете воспроизвести все расстояния в точности. Качество точки определяется как отношение квадрата расстояния - от данной точки до начала координат в пространстве выбранной размерности - к квадрату расстояния до начала координат, определенному в пространстве максимальной размерности (помните, что в качестве метрики в этом случае выбрана метрика Хи-квадрат, как уже упоминалось ранее). По аналогии с Факторным анализом качество точки похоже по интерпретации на показатель общности переменной в факторном анализе.
Заметим, что величина качества не зависит от выбранного метода стандартизации и всегда использует стандартизацию, установленную по умолчанию (т.е. метрикой расстояния является Хи-квадрат, и мера качества может интерпретироваться как доля Хи-квадрат, определяемая соответствующей строкой в пространстве соответствующей размерности). Низкое качество означает, что имеющееся число измерений недостаточно хорошо представляет соответствующую строку (столбец). В предыдущей таблице качество для первой строки (Старшие менеджеры) меньше 0.1, и это говорит о том, что данная точка плохо представлена в пространстве размерности единица.
Относительная инерция.
Относительная инерция.
Качество точки (см. выше) представляет отношение вклада данной точки в общую инерцию (Хи-квадрат), что может объяснять выбранную размерность. Однако, качество не отвечает на вопрос насколько, в действительности, и в каких размерах соответствующая точка вносит вклад в инерцию (величину Хи-квадрат). Относительная инерция представляет долю общей инерции, принадлежащую данной точке, и не зависит от выбранной пользователем размерности. Отметим, что какое-либо частное решение может достаточно хорошо представлять точку (высокое качество), но та же точка может вносить очень малый вклад в общую инерцию (т.е.
точка-строка, элементами которой являются относительные частоты, имеет сходство с некоторой строкой, элементы которой представляют собой среднее по всем строкам).
Относительная инерция для каждой размерности.
Относительная инерция для каждой размерности.
Данный столбец содержит относительный вклад соответствующей точки-строки в величину инерции, обусловленный соответствующей размерностью. В отчете данная величина приводится для каждой точки (строки или столбца) и для каждого измерения.
Косинус2 (качество или квадратичные корреляции с каждой размерностью).
Косинус2 (качество или квадратичные корреляции с каждой размерностью).
Данный столбец содержит качество для каждой точки, обусловленное соответствующей размерностью. Если просуммировать построчно элементы этих столбцов для каждой размерности, то в результате получим столбец величин Качество, о которых уже упоминалось выше (так как в рассматриваемом примере была выбрана размерность 1, то столбец Косинус2 совпадает со столбцом Качество). Эта величина может интерпретироваться как "корреляция" между соответствующей точкой и соответствующей размерностью. Термин Косинус2 возник по причине того, что данная величина является квадратом косинуса угла, образованного данной точкой и соответствующей осью (см. Greenacre, 1984, для детального анализа геометрической интерпретации анализа соответствий).
Замечание о "статистической значимости".
Замечание о "статистической значимости".
Необходимо отметить, что анализ соответствий является разведочным методом. Данный метод был разработан на базе методологии, рассматривающей построение моделей с точки зрения их соответствия данным, а не наоборот ("второй принцип" Benzerci постулирует так: "Модель должна удовлетворять имеющимся данным, а не наоборот"; см. Greenacre, 1984, стр.10). Следовательно, не существует статистических тестов, которые могли бы быть использованы для проверки результатов анализа соответствий. Главной целью анализа соответствий является представление в упрощенном виде (пространстве меньшей размерности) информации, содержащейся в больших частотных таблицах (или таблицах с аналогичными мерами соответствия).
| В начало |
Дополнительные точки
Дополнительные точки
Во Вводном обзоре описано, как интерпретировать координаты и связанные с ними статистики. Дополнительную помощь в интерпретации результатов может оказать включение дополнительных точек-строк или столбцов, которые на первоначальном этапе не участвовали в анализе. Например, рассмотрим следующие результаты, основанные на примере, использованном в водном разделе (см. также работу Greenacre, 1984).
Таблица 7
Таблица 7
| -.065768 .258958 -.380595 .232952 -.201089 |
.193737 .243305 .010660 -.057744 -.078911 |
| -.258368 | -.117648 |
Данная таблица отображает координаты (для двух размерностей), вычисленные для таблицы частот, состоящей из классификации степени пристрастия к курению среди сотрудников различных должностей. Строка Национальное среднее содержит координаты дополнительной точки, которая является национальным средним уровнем (в процентах) по различным категориям курящих (Национальное среднее - среднее для разных национальностей курящих, вымышленные цифры, приведенные в Greenacre, 1984, таковы: Некурящие - 42%, легко курящие - 29%, средне курящие - 20%, сильно курящие - 9%). Если вы построите двумерную диаграмму групп сотрудников и Национального среднего, то сразу убедитесь в том, что данная дополнительная точка и группа Секретари очень близки друг к другу и по одну сторону горизонтальной оси координат с категорией Некурящие (точкой-столбцом). Другими словами, выборка представленная в исходной частотной таблице содержит больше курящих, чем Национальное среднее.
Хотя такое же заключение можно сделать, взглянув на исходную таблицу сопряженности, в таблицах больших размеров подобные выводы, конечно, не столь очевидны.
Качество представления дополнительных точек.
Качество представления дополнительных точек.
Еще одним интересным результатом, касающимся дополнительных точек, является интерпретация качества, представления при заданной размерности (см. Вводный обзор для более подробного обсуждения концепции качества представления).
Повторим еще раз, что целью анализа соответствий является представление расстояний между координатами строк или столбцов в пространстве более низкой размерности. Зная, как решается данная задача, необходимо ответить на вопрос, является ли адекватным (в смысле расстояний до точек в исходном пространстве) представление дополнительной точки в пространстве выбранной размерности. Ниже представлены статистики для исходных точек и для дополнительной точки Национальное среднее для задачи в двумерном пространстве.
Таблица 8
Таблица 8
| .892568 .991082 .999817 .999810 .998603 |
.092232 .526400 .999033 .941934 .865346 |
.800336 .464682 .000784 .057876 .133257 |
| .761324 | .630578 | .130746 |
Все вышеперечисленные статистики уже обсуждались в вводном обзоре. Напомним, что качество точек-строк или столбцов определено, как отношение квадрата расстояния от точки до начала координат, в пространстве сниженной размерности, к квадрату расстояния от точки до начала координат, в исходном пространстве (помните, что в качестве метрики выбирается расстояние Хи-квадрат). В определенном смысле, качество является величиной, объясняющей долю квадрата расстояния до центра масс. Дополнительная точка-строка Национальное среднее имеет качество, равное .76, это означает, что данная точка достаточно хорошо представлена в двумерном пространстве. Статистика Косинус**2 - это качество представления соответствующей точки-строки, обусловленное выбором пространства заданной размерности (если просуммировать построчно элементы столбцов Косинус2 для каждого измерения, то в результате получим столбец величин Качество).
| В начало |
Многомерный анализ соответствий (МАС)
Многомерный анализ соответствий (МАС)
Многомерный Анализ Соответствий (МАС) можно рассматривать как обобщение анализа соответствий на случай более одной размерности.
Для ознакомления с анализом соответствий обратитесь к разделу Вводный обзор. Многомерный анализ соответствий - это анализ соответствий на бинарной (индикаторной) матрице, где объекты расположены по строкам, а группирующие переменные по столбцам. Обычно в анализе используется не матрица в бинарной форме, а матрица Берта (Burt), которая получается в результате матричного умножения транспонированной матрицы на исходную бинарную матрицу. Однако для простоты интерпретации результатов многомерного анализа соответствий, мы будем обсуждать применение анализа соответствий на примере бинарной матрицы.
Бинарная или индикаторная матрица.
Бинарная или индикаторная матрица.
Рассмотрим пример простой двухвходовой матрицы, рассмотренный во вводном обзоре.
Таблица 9
Таблица 9
| 4 4 25 18 10 |
2 3 10 24 6 |
3 7 12 33 7 |
2 4 4 13 2 |
11 18 51 88 25 |
| 61 | 45 | 62 | 25 | 193 |
Допустим, что вы представили эти данные в виде бинарной матрицы.
Таблица 10
Таблица 10
| 1 1 1 1 1 . . . 0 0 0 |
0 0 0 0 0 . . . 0 0 0 |
0 0 0 0 0 . . . 0 0 0 |
0 0 0 0 0 . . . 0 0 0 |
0 0 0 0 0 . . . 1 1 1 |
1 1 1 1 0 . . . 0 0 0 |
0 0 0 0 1 . . . 0 0 0 |
0 0 0 0 0 . . . 1 0 0 |
0 0 0 0 0 . . . 0 1 1 |
Каждый из 193 объектов записан в этой матрице.
Если объект принадлежит некоторой категории, то элемент на пересечении соответствующей строки и столбца равен 1, в противном случае 0. Например, объект 1 представляет Старшего менеджера, который принадлежит категории Некурящие. Как легко определить по исходной двухвходовой матрице, всего имеется 4 таких наблюдения, и, следовательно, имеется четыре объекта в бинарной матрице.
Анализ бинарной матрицы.
Анализ бинарной матрицы.
Если бы вы анализировали рассматриваемый файл (бинарную матрицу) как двухвходовую таблицу, то в качестве результатов получили бы столбцы координат, которые позволили бы связать различные категории друг с другом, основываясь на расстояниях между точками-строками, т.е. между индивидуальными объектами. В действительности, вид столбцов координат был бы очень похож на столбцы координат, получаемые в результате применения анализа соответствий к двухвходовой частотной таблице (заметим, что метрики в рассматриваемых пространствах будут различны, однако, относительное расположение точек схоже).
Более чем две переменных.
Более чем две переменных.
Подход, который мы наметили, для анализа группированных данных, можно легко распространить на случай более двух переменных. Например, бинарная матрица может дополнительно включать переменные Мужчина и Женщина, которые аналогично кодируются 0 или 1, или еще три переменные обуславливающие принадлежность к той или иной возрастной группе. Таким образом, окончательный результат может представлять взаимосвязи между переменными Пол, Возраст, Склонность к курению и Занимаемая должность (Группа сотрудников).
Нечеткое кодирование.
Нечеткое кодирование.
Каждый объект не обязательно должен принадлежать какой-либо одной категории рассматриваемой категоризованной переменной. Помимо кодировки 0 или 1, возможно ввести вероятностное распределение на категориях переменной или какую-либо другую меру, реализующую нечеткое правило для принадлежности к той или иной группе. Greenacre (1984) в своей работе рассмотрел различные схемы такого кодирования.
Например, допустим, что в рассмотренной выше бинарной матрице, имеются пропущенные данные, относящиеся к типам курящих. Вместо исключения попущенных данных из анализа (или создания новой категории Пропущенные данные), вы можете приписать данным пропущенным категориям некоторые числа (дающие в сумме 1), интерпретируемые как вероятности того, что соответствующий объект попадает в данную категорию (например, вы можете приписывать вероятности, основываясь на информации об оценках средних величин для всего населения по категориям).
Интерпретация координат и другие результаты.
Интерпретация координат и другие результаты.
Повторим, что результаты, полученные методом многомерного анализа соответствий для координат точек, идентичны результатам применения анализа соответствий к бинарной матрице. Следовательно, интерпретация координат, качества, квадратов косинусов и других статистик анализа соответствий полностью переносится на случай многомерного анализа соответствий (см. Вводный обзор), заметим только, что вышеперечисленные статистики, в случае многомерного анализа соответствий, относятся к инерции всей бинарной матрицы.
Дополнительные точки-столбцы и "множественная регрессия" группирующих переменных.
Дополнительные точки-столбцы и "множественная регрессия" группирующих переменных.
Еще одним применением бинарных матриц служит возможность применения метода, эквивалентного методу Множественной регрессии для группирующих переменных путем добавления дополнительных точек-столбцов к бинарной матрице. Например, предположим, что вы добавили к бинарной матрице еще два столбца, чтобы ответить на вопрос, болел или нет опрашиваемый в течение прошедшего года (т.е. вы добавляете столбец с именем Болен и столбец с именем Не болен и, как обычно, используете 1 или 0 для обозначения принадлежности к той или иной категории). Применяя анализ соответствий для рассматриваемой бинарной матрицы, во-первых, вы можете объяснить влияние других показателей на показатель заболеваемости с помощью качества представления (см. Вводный обзор), и, во-вторых, отображение координат дополнительных точек может указать природу (направление) зависимостей между столбцами бинарной матрицы и столбцами дополнительных точек, отражающими заболеваемость.
Добавление дополнительных точек в МАС анализ иногда называют предсказывающим отображением.
Матрица Берта. Реальные вычисления в многомерном анализе соответствий не используют индикаторную матрицу (которая может быть очень большой, если рассматривается много объектов и переменных). Для вычислений используется матричное произведение транспонированной и исходной бинарной матрицы или матрица Берта. Данная квадратная матрица табулирует связи между всеми имеющимися категориям. Для двухвходовой таблицы, рассмотренной ранее, матрица Берта имеет следующий вид:
Таблица 11
Таблица 11
| 11 0 0 0 0 4 2 3 2 |
0 18 0 0 0 4 3 7 4 |
0 0 51 0 0 25 10 12 4 |
0 0 0 88 0 18 24 33 13 |
0 0 0 0 25 10 6 7 2 |
4 4 25 18 10 61 0 0 0 |
2 3 10 24 6 0 45 0 0 |
3 7 12 33 7 0 0 62 0 |
2 4 4 13 2 0 0 0 25 |
Матрица Берта имеет достаточно очевидную структуру. В случае двух группирующих переменных (как показано выше), матрица Берта состоит из четырех блоков: подматрица кросстабуляции переменной Сотрудники с переменной Сотрудники, подматрица кросстабуляции переменной Сотрудники с переменной Курящие, подматрица кросстабуляции переменной Курящие с переменной Сотрудники и подматрица кросстабуляции переменной Курящие с переменной Курящие. Заметим, что данная матрица симметрична и что суммы диагональных элементов в каждом блоке, представляющем кросстабуляцию некоторой переменной с собой, равны (например, в данном примере размер выборки был равен 193, и, следовательно, суммы диагональных элементов подматриц кросстабуляции переменных Сотрудники с собой и Курящие с собой эквивалентны и равны 193).
Внедиагональные элементы подматриц, представляющих кросстабуляцию переменных с собой, равны 0. Однако это не является правилом, например, когда матрица Берта получена из бинарной матрицы, включающей нечеткое кодирование принадлежности категории (см.
выше), в этом случае внедиагональные элементы могут отличаться от 0.
| В начало |
Матрица Берта
Матрица Берта
Многомерный анализ соответствий использует в качестве входного формата данных (т.е. преобразует произвольные данные к такому формату) матрицу Берта. Матрица Берта является квадратом бинарной матрицы, поэтому результаты применения многомерного анализа соответствий аналогичны результатам анализа соответствий для точек-столбцов бинарной матрицы (см. также раздел МАС).
Например, допустим, что вы ввели данные по выживанию различных возрастных групп в различных городах.
Таблица 12
Таблица 12
| 0 1 0 0 . . . 1 0 0 |
1 0 1 1 . . . 0 1 1 |
0 1 0 0 . . . 0 1 0 |
1 0 1 0 . . . 1 0 1 |
0 0 0 1 . . . 0 0 0 |
0 1 0 0 . . . 1 0 0 |
0 0 1 0 . . . 0 1 0 |
1 0 0 1 . . . 0 0 1 |
В данной таблице 1 обозначает, что данный субъект принадлежит соответствующему множеству категорий (например, Выжил имеет категории Да и Нет). Например, первый субъект выжил (т.к. 0 находится в категории Нет, 1 в категории Да), в том же случае, субъект находится в возрасте от 50 до 69 лет (1 установлена в категории От50до60) и проживает в Милане. Выборка состоит из 764 субъектов.
Если вы обозначите данные (бинарную матрицу) в рассматриваемом примере как матрица X, то матричное произведение X'X является матрицей Берта. Ниже приведена матрица Берта для данного примера.
Таблица 13
Таблица 13
| 210 0 68 93 49 60 82 68 |
0 554 212 258 84 230 171 153 |
68 212 280 0 0 151 58 71 |
93 258 0 351 0 120 122 109 |
49 84 0 0 133 19 73 41 |
60 230 151 120 19 290 0 0 |
82 171 58 122 73 0 253 0 |
68 153 71 109 41 0 0 221 |
Структура рассматриваемой матрицы Берта очевидна. Данная матрица симметрична. В случае 3 группирующих переменных (как в рассматриваемом примере) матрица данных состоит из 3 x 3 = 9 блоков, которые образуются в результате взаимной кросстабуляции имеющихся группирующих переменных. Заметим, что суммы диагональных элементов каждого диагонального блока (т.е. в тех блоках, где переменные кросстабулированы сами с собой) постоянны и равны 764 для данного случая.
Все внедиагональные элементы, принадлежащие диагональным блокам, равны 0. Если же объекты некоторой бинарной матрицы кодировались с помощью процедуры нечеткого кодирования (т.е. если принадлежность объекта категории определялась некоторой вероятностью), то равенство 0 внедиагональных элементов диагональных блоков не гарантировано.
| В начало |

(c) Copyright StatSoft, Inc., 1984-2001
STATISTICA является торговой маркой StatSoft, Inc.