Иллюстрированный самоучитель по Maple
Реализация итераций Ньютона в символьном виде
Найти достаточно простую и наглядную задачу, решение которой отсутствует в системе Maple 7, не очень просто. Поэтому для демонстрации решения задачи с применением аналитических методов воспользуемся примером, ставшим классическим, — реализуем итерационный метод Ньютона при решении нелинейного уравнения вида f(x) - 0.
Как известно, метод Ньютона сводится к итерационным вычислениям по следующей формуле:
xi+1=x1+f(x1)/f'(x1);
Реализующая его процедура выглядит довольно просто:
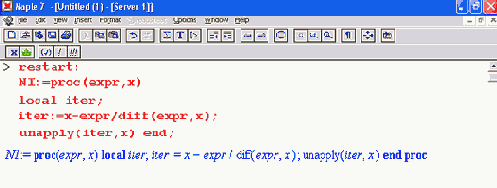
Для получения итерационной формулы в аналитическом виде здесь используется функция unapply. Теперь, если задать решаемое уравнение, то можно получить искомое аналитическое выражение:
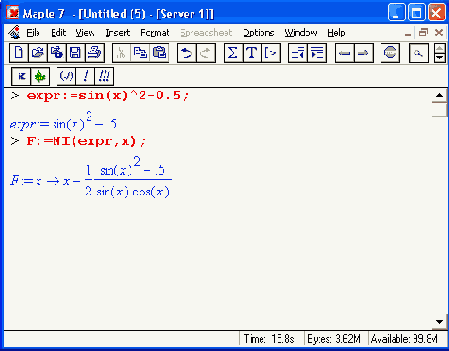
Далее, задав начальное приближение для х в виде х = х0, можно получить результаты вычислений для ряда итераций:
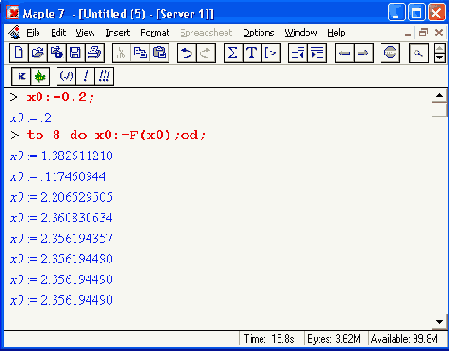
Нетрудно заметить, что, испытав скачок в начале решения, значениях довольно быстро сходятся к конечному результату, дающему корень заданной функции. Последние три итерации дают одно и то же значение х. Заметим, что этот метод дает только одно решение, даже если корней несколько. Вычислить другие корни в таком случае можно, изменив начальное условие.
Можно попробовать с помощью полученной процедуры получить решение и для другой функции:
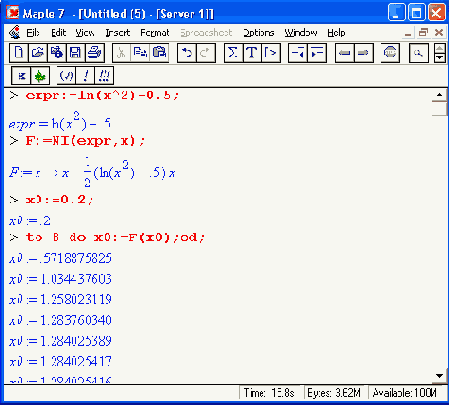
Здесь итерационная формула имеет (и вполне естественно) уже другой вид, но сходимость к корню также обеспечивается за несколько итераций. ;
Возможна и иная форма задания итерационной процедуры с применением оператора дифференцирования D и заданием исходной функции также в виде процедуры:
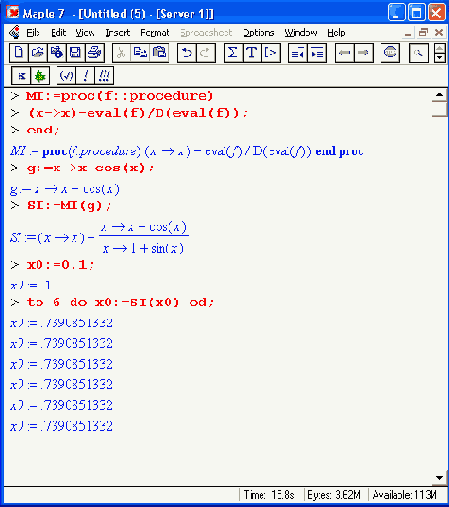
Вообще говоря, в программных процедурах можно использовать любые операторы и функции, присущие Maple-языку, в том числе и те, которые реализуют символьные вычисления. Это открывает широкий простор для разработки новых процедур и функций, обеспечивающих выполнение символьных операций.