Иллюстрированный самоучитель по Maple
Графики нескольких функций на одном рисунке
Важное значение имеет возможность построения на одном рисунке графиков нескольких функций. В простейшем случае (рис. 11.4, первый пример) для построения таких графиков достаточно перечислить нужные функции и установить для них общие интервалы изменения.
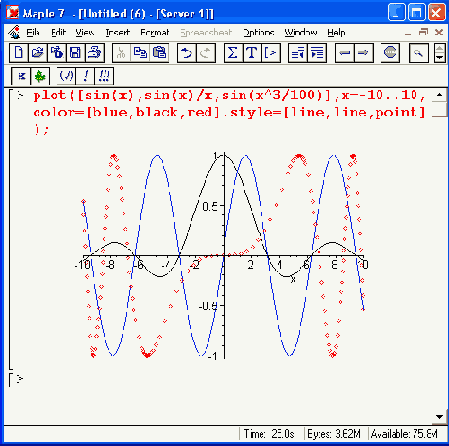
Рис. 11.4. Графики трех функций на одном рисунке
Обычно графики разных функций автоматически строятся разными цветами. Но это не всегда удовлетворяет пользователя — например, при распечатке графиков монохромным принтером некоторые кривые могут выглядеть слишком блеклыми или даже не пропечататься вообще. Используя списки параметров color (цвет линий) и style (стиль линий), можно добиться выразительного выделения кривых — это показывает второй пример на рис. 11.4 для случая, когда линии графиков выделяются стилем. Однако если кривые задаются разным цветом, то при черно-белой печати они могут перестать различаться.
На рис. 11.5 показан еще один пример такого рода. Здесь построен график функции sin(x)/x и график ее полиномиальной аппроксимации. Она выполняется настолько просто, что соответствующие функции записаны прямо в списке параметров функции plot.
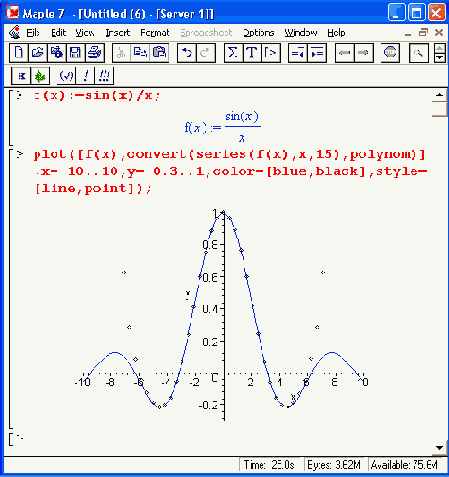
Рис. 11.5. График функции sin(x)/x и ее полиномиальной аппроксимации
В данном случае сама функция построена сплошной линией, а график полинома точками — ромбами. Хорошо видно, что при малых х аппроксимация дает высокую точность, но затем с ростом х ее погрешность резко возрастает.
Рисунок 11.6 показывает построение нескольких любопытных функций, полученных с помощью комбинаций элементарных функций. Такие комбинации позволяют получать периодические функции, моделирующие сигналы стандартного вида: в виде напряжения на выходе двухполупериодного выпрямителя, симметричных прямоугольных колебаний (меандр), пилообразных и треугольных импульсов, треугольных импульсов со скругленной вершиной.
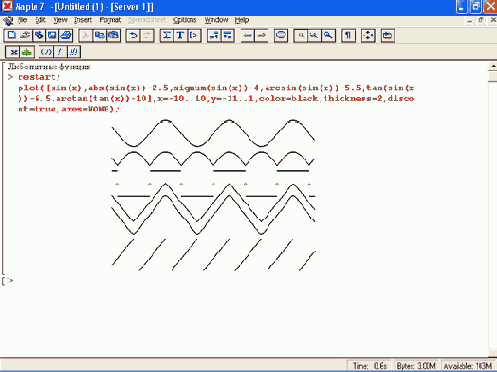
Рис. 11.6. Построение графиков нескольких любопытных функций
В этом рисунке запись axes=NONE убирает координатные оси. Обратите внимание, что смещение графиков отдельных функций вниз с целью устранения их наложения достигнуто просто прибавлением к значению каждой функции некоторой константы.