Иллюстрированный самоучитель по Maple
Визуализация дифференциальных параметров кривых
Дифференциальные параметры функции f(x), описывающей некоторую кривую, имеют большое значение для анализа ее особых точек и областей существования. Так, точки с нулевой первой производной задают области, где кривая нарастает (первая производная положительна) или убывает (первая производная отрицательна) с ростом аргументах. Нули второй производной задают точки перегиба кривой.
Следующая графическая процедура служит для визуализации поведения кривой /, = /(.г) на отрезке изменениях от а до b:
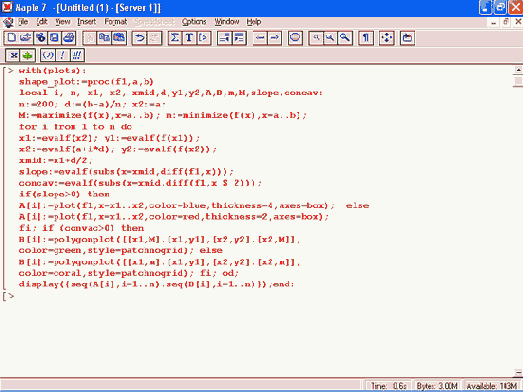
В этой процедуре заданы следующие цвета (их можно изменить): Таблица 12.1. Цвета при визуализации в процедуре shape_plot
| Изменение /(х) |
Цвет |
| Возрастание |
Синий |
| Убывание |
Красный |
| Площадь |
Цвет |
| Над минимумом |
Зеленый |
| Под максимумом |
Коралловый |
Например, для функции:
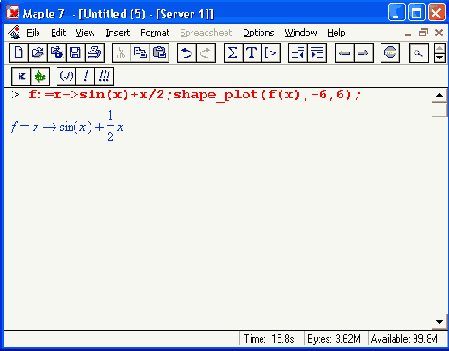
построенный график будет иметь вид, представленный на рис. 12.43 (естественно, в книге цвета — лишь оттенки серого).
Рисунок 12.43 дает наглядное представление о поведении заданной функции. Рекомендуется опробовать данную процедуру на других функциях. Следует отметить, что, поскольку процедура использует функции ntiroimize и maximize, она может давать сбои при исследовании сложных функций, содержащих специальные математические функции или особенности. Иногда можно избежать такой ситуации, исключив особенность. Например, для анализа функции sin(x)/x можно записать ее в виде:
>f:=x->if x=0 then 1 else sin(x)/x
end if;
shape_plot(f(x),-10,10);
Исполнение приведенной выше строки ввода дает график, представленный на рис. 12.44.
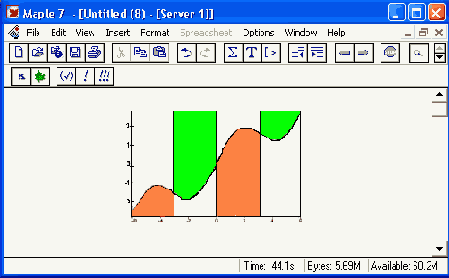
Рис. 12.43. Визуализация поведения функции f(х)
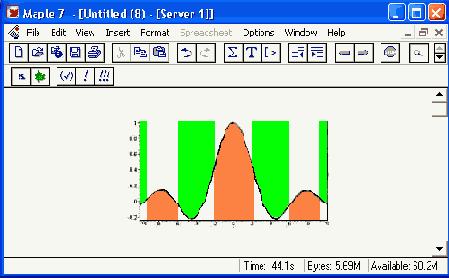
Рис. 12.44. Визуализация поведения функции sin(x)/x
Данная процедура дает хорошие результаты при анализе функций, представленных полиномами. Вы можете сами убедиться в этом.
 |
 |
 |