Иллюстрированный самоучитель по Maple
Паде-аппроксимация аналитических функций
Для аппроксимации аналитических функций одной из лучших является Паде-аппроксимация, при которой заданная функция приближается отношением двух полиномов. Для осуществления такой аппроксимации используется функция pade:
pade(f. x=a, [m.n])
pade(f.,х, [m.n])
Здесь f — аналитическое выражение или функция, х — переменная, относительно которой записывается аппроксимирующая функция, а — координата точки, относительно которой выполняется аппроксимация, m, n — максимальные степени полиномов числителя и знаменателя. Технику аппроксимации Паде поясняет рис. 14.4.
На рис. 14.4 представлена аппроксимация синусоидальной функции, а также построены графики этой функции и аппроксимирующей функции. Под ними дан также график абсолютной погрешности для этого вида аппроксимации. Нетрудно заметить, что уже в интервале [-л, я] погрешность резко возрастает на концах интервала аппроксимации.
Важным достоинством Паде-аппроксимации является возможность довольно точного приближения разрывных функций. Это связано с тем, что нули знаменателя у аппроксимирующего выражения способны приближать разрывы функций, если на заданном интервале аппроксимации число разрывов конечно. На рис. 14.5 представлен пример Паде-аппроксимации функции tan(x) в интервале от -4,5 до 4,5, включающем два разрыва функции.
Как видно из рис. 14.5, расхождение между функцией тангенса и ее аппроксимирующей функцией едва заметно лишь на краях интервала аппроксимации. Оба разрыва прекрасно приближаются аппроксимирующей функцией. Такой характер аппроксимации подтверждается и графиком погрешности, которая лишь на концах интервала аппроксимации [-4,0, 4,0] достигает значений 0,01 (около 1%).
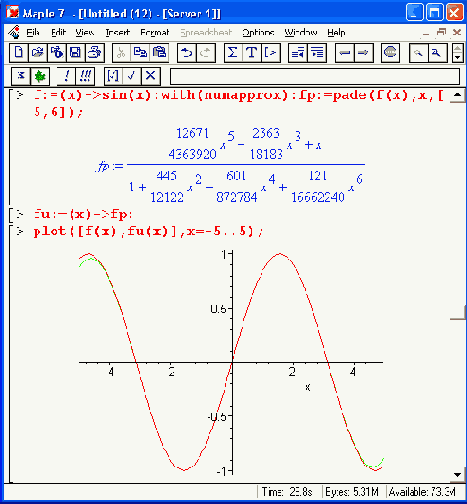
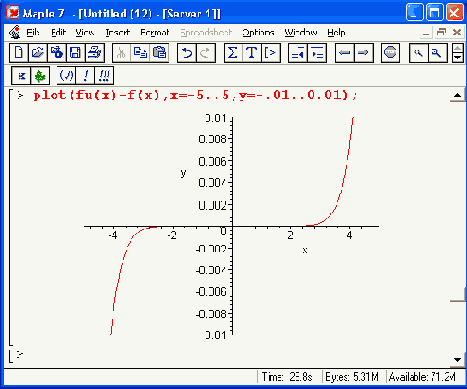
Рис. 14.4. Аппроксимация Паде для синусоидальной функции
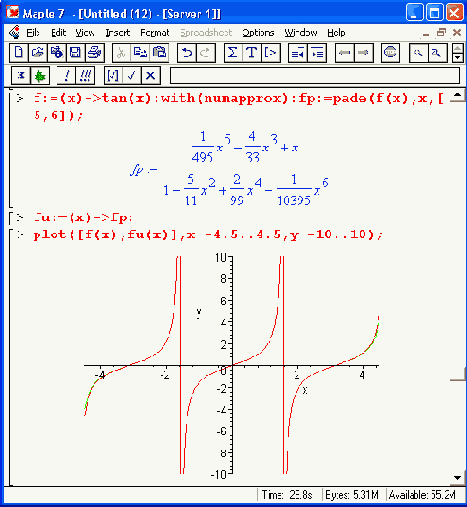
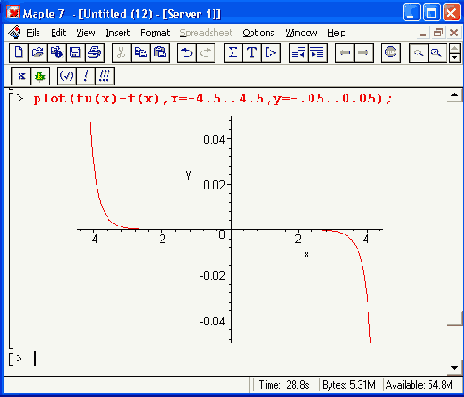
Рис. 14.5. Аппроксимация Паде для разрывной функции тангенса