Прочие функции пакета simplex

Функция basis(C) возвращает базис для системы линейных уравнений С. Например:

> basisC [ х - 2*z+w , z - 2*у - w ] );

[x,z] 

Функция convexhull(ps) возвращает выпуклую оболочку множества точек ps:

> convexhum{[0,0],[l,l],[2,-l],[1,1/3],[1,1/2]}):

 [[0,0],[2,-1],[1, 1]]

Для определения констант для системы линейных уравнений или неравенств служит функция cterm(C):

> cterm([2*х+у<=6.7*y-z-3-4]);

 [6,7]

Функция define_zero(C) возвращает ближайшее ненулевое значение, зависящее от установки переменной Digits: 

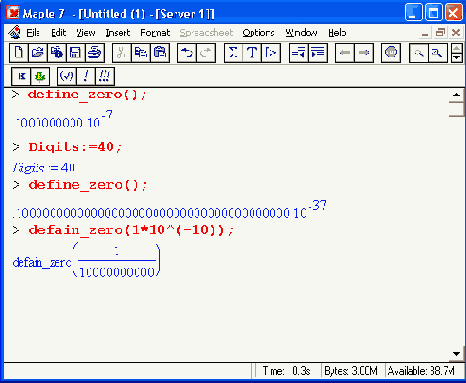
Функция display(C) имеет еще и форму display(C,[X, у, z]). Она задает вывод линейных уравнений и неравенств в матричной форме:

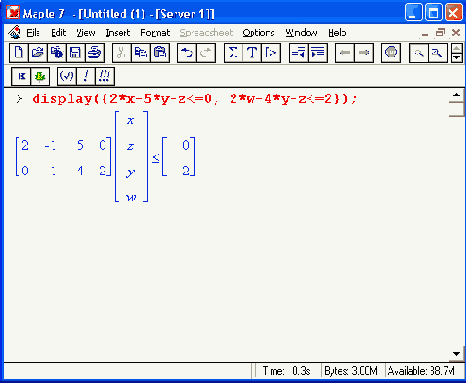
Функция dual(f, С, у) имеет следующие параметры: f — линейное выражение y, С  множество неравенств и у — имя. Эта функция возвращает сопряженное с f выражение:

> dual( x-y,{2*x+3*y<=5.3*x+6*y<=15},z);

115zl +5z2, {1_<3z1+2z2,-l_<6z1+3z2}

Функция feasible может быть задана в трех формах:

feasible(C)

feasible(C,vartype)

feasible(C,vartype,'NewC','Transform')

Здесь параметр vartype может иметь значения NONNEGATIVE или UNRESTRICTED. Эта функция определяет систему как осуществимую или нет:

> feasible({2*x+3*y<-5, 3*x+6*y<"15}, NONNEGATIVE);

true

> feasib1e({2*x+3*y<-5, 3*х+б*у<—15}, NONNEGATIVE);

false

Если функция возвращает логическое значение true, то заданная система осуществима, а если false — неосуществима, то есть ни при каких значениях переменных не способна удовлетворить записанным неравенствам и равенствам. Функция pivot (С, х, eqn) конструирует новую систему с заданным главным элементом:

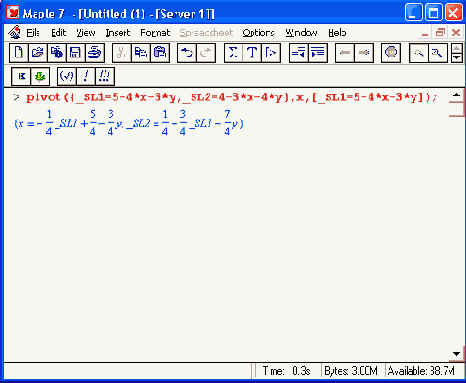
Функция pivoteqn(C, var) возвращает подсистему для заданного диагонального элемента С:

> pivoteqnC {_SL1 - 5-3*х-2*у. _SL2 - 4-2*х-2*у}. х ); 

[_SLl = 5-lx-2y] 

Функция pivotvar(f, List) или pivotvar(f) возвращает список переменных, имеющих положительные коэффициенты в выражении для целевой функции:

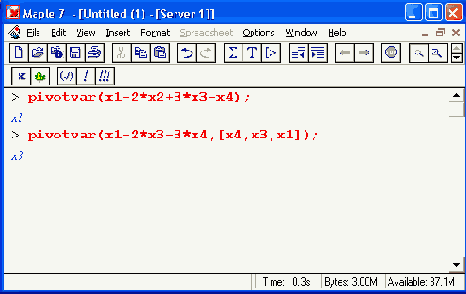
Функция ratio(C, x) возвращает список отношений, задающих наиболее жесткие ограничения:

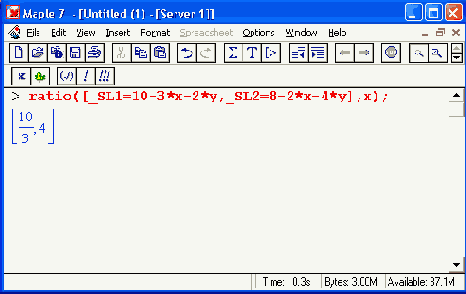
Функция setup может иметь три формы:

setup(C)

setup(C, NONNEGATIVE)

setup(C, NONNEGATIVE, 't')

Она обеспечивает конструирование множества уравнений с переменными в левой части:



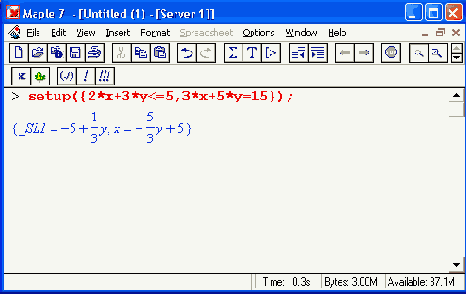
Последняя функция — standartlze(C) — конвертирует список уравнений (неравенств) в неравенства типа «меньше или равно»:

> standardize({2*x+3*y<-5.3*x+5*yl5});

{2х + Зу<5,Зх + 5у<15,-Зх-5у<-15}



Содержание раздела

---

---