Иллюстрированный самоучитель по Maple
Моделирование цепи на туннельном диоде
А теперь займемся моделированием явно нелинейной цепи. Выполним его для цепи, которая состоит из последовательно включенных источника напряжения Es, резистора Rs, индуктивности L и туннельного диода, имеющего N-образную вольтамперную характеристику (ВАХ). Туннельный диод обладает емкостью С, что имитируется конденсатором С, подключенным параллельно туннельному диоду. Пусть ВАХ реального туннельного диода задана выражением:
> restart:
> A:=.3t: а:=10: В:=1*10^(-8): b:=20:
> Id:=Ud->A*Ud*exp(-a*Ud)+B*(exp(b*Ud-D):
Id:=Ud->AUde(-aUd)+Be(bUd-1)
Построим график ВАХ:
> plot(Id(Ud), Ud=-.02..0.76,color=black):
Этот график представлен на рис. 17.25. Нетрудно заметить, что ВАХ туннельного диода не только резко нелинейна, но и содержит протяженный участок отрицательной дифференциальной проводимости, на котором ток падает с ростом напряжения. Это является признаком того, что такая цепь способна на переменном токе отдавать энергию во внешнюю цепь и приводить к возникновению колебаний в ней различного типа.
Работа цепи описывается системой из двух дифференциальных уравнений:
di/dt=(Es-i(t)*Rs-u(t))/L
du/dt=(i(t)-Id(u(t))/C
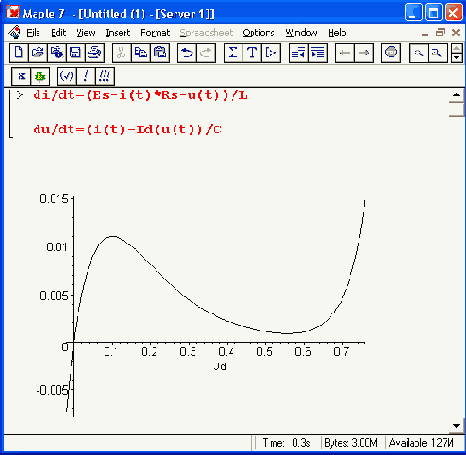
Рис. 17.25. ВАХ туннельного диода
Пусть задано Es = 0,35 В, Rs= 15 Ом, С = 10*10-12, L = 30*10-9 и максимальное время моделирования tm=10*10-9. Итак, задаем исходные данные:
> Es:=.35:Rs:=15:C:=10*10^(-12):L:=30*10^(-6):tm:=10*10^(-9):
Составим систему дифференциальных уравнений цепи и выполним ее решение с помощью функции dsolve:
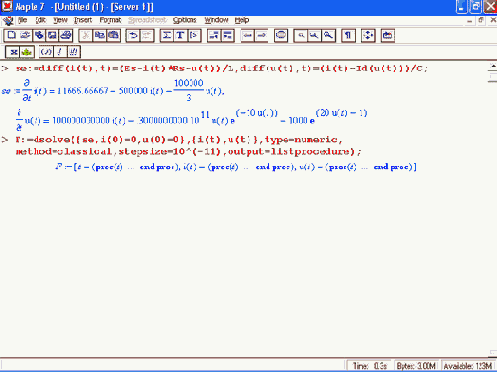
Поскольку заведомо известно, что схема имеет малые значения L и С, мы задали с помощью параметров достаточно малый шаг решения для функции dsolve — stepsize=l(T(-11) (с). При больших шагах возможна численная неустойчивость решения, искажающая форму колебаний, получаемую при моделировании. Используя функции odeplot и displ ay пакета plots, построим графики решения в виде временных зависимостей u(t) и 10*i (t) и линии, соответствующей напряжению Es источника питания:
> gu:=odeplot(F,[t,u(t)],0,tm,color=black,
labels=['tVu(t),10*i(tr]):
> gi:=odeplot(F,[t,10*i(t)],0..tm.color-black):
> ge:=odeplot(F,[t,Es].0..tm.color=red): .
> display(gu.gi,ge);
Эти зависимости представлены на рис. 17.26. Из них хорошо видно, что цепь создает автоколебания релаксационного типа. Их форма сильно отличается от синусоидальной.
Решение можно представить также в виде фазового портрета, построенного на фоне построенных ВАХ и линии нагрузки резистора Rs:
> gv:=plot({Id(Ud),(Es-Ud)/Rs},Ud=-.05..0.75,color=black,
labels=[Ud,Id]):
> gpp:=odeplot(F.[u(t),i(t)],0..tm,color=blue):
> display(gv,gpp);
Фазовый портрет колебаний показан на рис. 17.27.
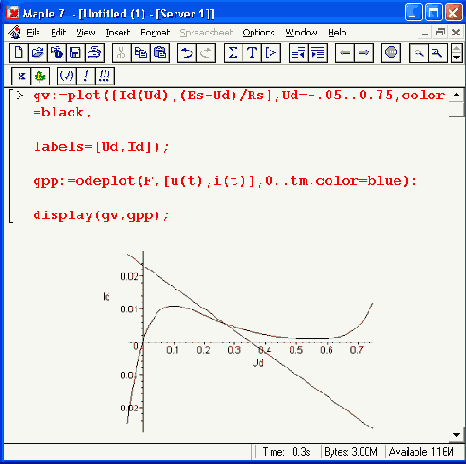
О том, что колебания релаксационные можно судить по тому, что уже первый цикл колебаний вырождается в замкнутую кривую — предельный цикл, форма которого заметно отличается от эллиптической.
Итак, мы видим, что данная цепь выполняет функцию генератора незатухающих релаксационных колебаний. Хотя поставленная задача моделирования цепи на туннельном диоде успешно решена, в ходе ее решения мы столкнулись с проблемой обеспечения малого шага по времени при решении системы дифференциальных уравнений, описывающих работу цепи. При неудачном выборе шага можно наблюдать явную неустойчивость решения.
 |
 |
 |