Средства контроля и отладки процедур

Большая часть функций и операторов системы Maple 7 реализована в виде процедур, написанных на Maple-языке программирования. Благодаря возможности их просмотра пользователь получает неисчерпаемый источник примеров программирования на этом языке. Кроме того, пользователь может создавать свои собственные процедуры.

Для контроля и отладки процедур прежде всего надо уметь вывести их текст. Для этого служит функция:

print(name);

где name — имя процедуры.

Однако перед тем, как использовать эту функцию, надо исполнить команду:

> interfасе(verboseproc=2,prettyprint-l.version);

Maple Worksheet Interface, Maple 7, IBM INTEL NT, May 28 2001 Build ID 96223

Ее смысл будет пояснен ниже. Пока же отметим, что эта команда обеспечивает полный вывод текста процедур библиотеки. Встроенные в ядро процедуры, написанные не на Maple-языке, в полном тексте не представляются. Поясним это следующими примерами:

> print(evalf);

proc() option builtin, remember; 167 end proc

> print(erf);

proc(x::algebraic)

local Re_x, Im_x, sr, si, xr, xi;

if nargs <> 1 then error "expecting 1 argument, got %1", nargs

elif type(x, 'complex(float)') then evalf('erf (x)) elif x = 0 then 0 elif type(x, 'infinity') then

if type(x, {'cxjnfinity', 'undefined'}) thenundefined + undefined*!

elif type(Re(x), 'infinity') then CopySign(l, Re(x))

elif type(x, 'imaginary') then x

else infinity + infinity*I

end if

elif type(x, 'undefined') then x*undefined elif type(x, 'complex(numeric)')

then

if csgn(x) = -1 then -erf(-x) else 'erf'(x)

end if elif type(x, '*')

and type(op(l, x), 'complex(numeric)')

and csgn(op(l, x)) = -1 then -erf(-x) elif type(x, ' +')

and traperror(sign(x)) = -1 then -erfC-x)

else erf(x) := 'erf'(x) end if end proc

Здесь вначале выполнен вывод сокращенного листинга встроенной в ядро процедуры evalf, а затем выведен полный листинг процедуры вычисления функции ошибок erf.
Эта функция имеет довольно короткую процедуру — многие важные функции и операторы задаются гораздо более сложными и большими процедурами.

Но вернемся к функции interface. Эта функция служит для управления выводом и задается в виде: interface( arg1. arg2, ... ) где аргументы задаются в виде равенств вида name=va1ue и слов-указателей:

ansi	autoassign	echo	error-break	errorcursor
imaginaryunit	indentamount	labelling	label width	latexwidth
"longdelim	patchl evel	plotdevice	plqtoptions	plotoutput
postplot	preplot	prettyprint	prompt	quiet
rtablesize	screenheight	screenwidth	showassuraed	verboseproc
version	warnl evel

К сожалению, объем и характер данной книги не позволяют остановиться на всех вариантах использования этой очень мощной функции, тем более что в ней может использоваться множество аргументов. Мы рассмотрим только некоторые, наиболее важные возможности.

Указание verboseproc=n задает степень детальности вывода листинга процедур. При n=0 текст не выводится, при n=1 выводится текст только заданных пользователем процедур, а при n=2 — всех процедур на Maple-языке. Пример этого был дан выше. Указание prettyprint=0 или 1 управляет выводом стандартных сообщений. Указание plotdevice=string управляет выводом графики, например plotdevice=gif указывает на то, что запись графиков в виде файлов будет происходить в формате .gif.

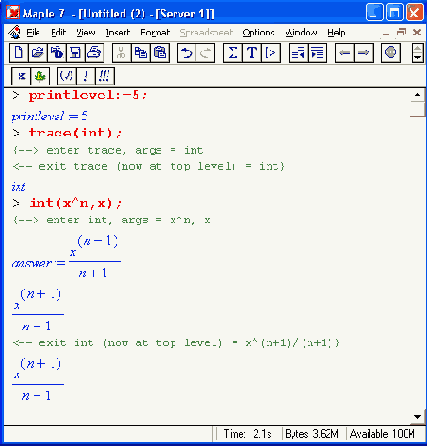
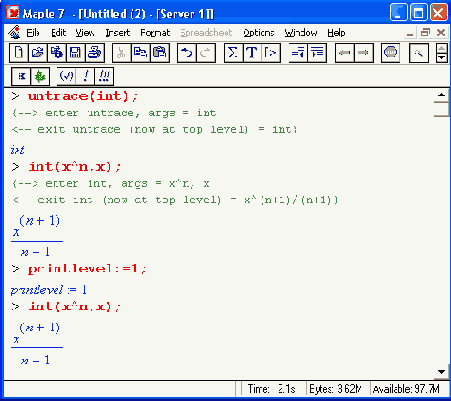
Одним из основных средств отладки процедур является функция трассировки trace(name). Детальность ее работы задается системной переменной printlevel (уровень вывода). При printlevel :=n (значение n = 1 по умолчанию) выводится результат только непосредственно исполняемой функции или оператора. Для вывода информации о выполнении k-ro уровня вложенности надо использовать значение этой переменной от 5*k до 5*(k+i). Так, при п от 1 до 5 выводятся результаты трассировки первого уровня, при и от 6 до 10 — второго и т. д. Максимальное значение п = 100 обеспечивает трассировку по всем уровням вложенности процедуры name.

Следующий пример показывает осуществление трассировки для функции int(x^n,x):

Действие функции трассировки отменяется командой untrace:

При отладке алгоритмов выполнения вычислений надо тщательно следить за сообщениями об ошибках. Для этого в Maple предусмотрены функция traceerr и системная переменная lasterr, в которой сохраняется последнее сообщение об ошибке. При каждом обращении к tracerr переменная lasterr очищается:

> 2/0;

Error, numeric exeption:division by zero

> 2/4;

1/2

> 2/.3;

6.666666667

> lasterror:

"division by zero"

> traperror(3/4);

3/4

> lasterror;

lasterror

> traperror(5/0);

Error, numeric exeption:division by zero

> lasterror:

"numeric exeption:division by zero"

Этот пример показывает, как может быть проведено отслеживание ошибок в ходе вычислений. Вообще говоря, пользователь системы Maple 7 редко привлекает описанные средства, поскольку проще отладить вычислительный алгоритм прежде, чем на его основе будет составлена процедура. При правильном построении процедур ошибочные ситуации заведомо предусматриваются и должным образом обрабатываются.

Содержание раздела