Иллюстрированный самоучитель по Maple
Функции дифференцирования выражений diff и Diff
Вычисление производных функций fn(x) = dfn(x)/dxn n-го порядка — одна из самых распространенных задач математического анализа. Для ее реализации Maple 7 имеет следующие основные функции:
diff(a., xl, х2, .... xn) diff(a, [xl, х2, .... хn])
Diff(a, xl, x2, .... xn) Diff(a, [xl, x2, .... хn])
Здесь а — дифференцируемое алгебраическое выражение, властности функция f(xl. x2, .... хn) ряда переменных, по которым производится дифференцирование. Функция Diff является инертной формой вычисляемой функции diff и может использоваться для естественного воспроизведения производных в документах. Первая из этих функций (в вычисляемой и в инертной форме) вычисляет частные производные для выражения а по переменным xl, х2, ..., .хn. В простейшем случае diff(f(x),x) вычисляет первую производную функции f(x) по переменной х. При n, большем 1, вычисления производных выполняются рекурсивно, например diff (f (х), х, у) эквивалентно diff(diff (f(x), х), у). Оператор $ можно использовать для вычисления производных высокого порядка. Для этого после имени соответствующей переменной ставится этот оператор и указывается порядок производной. Например, выражение diff (f(x) ,x$4) вычисляет производную 4-го порядка и эквивалентно записи diff (f (х) ,х,х,х.х). A diff (g(x,y) ,x$2,y$3) эквивалентно diff(g(x,y),x,x.y,y,y) ;
Примеры вычисления производных:
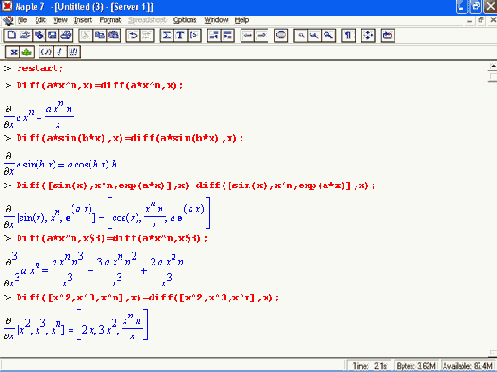
Как видно из приведенных примеров, функции вычисления производных могут использоваться с параметрами, заданными списками. Приведенные ниже примеры показывают эти возможности и иллюстрируют дифференцирование функции пользователя для двух переменных:
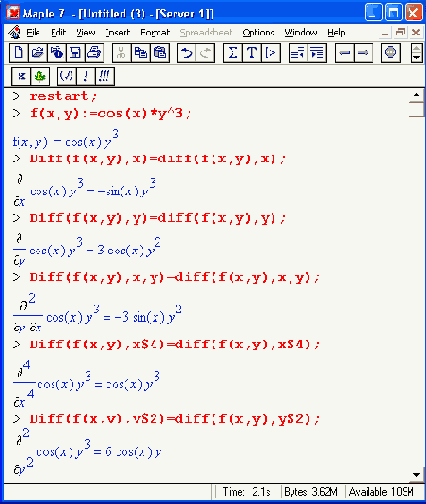
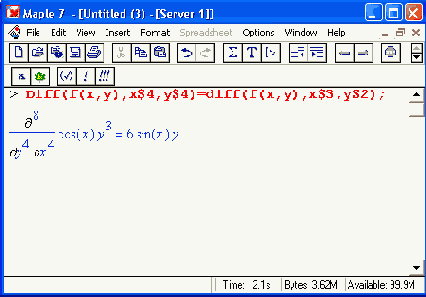
Получаемые в результате дифференцирования выражения могут входить в другие выражения. Можно задавать их как функции пользователя и строить графики производных.