Иллюстрированный самоучитель по Maple
Разложение в степенной ряд
Огромное разнообразие функций давно заставляло математиков задумываться над возможностями их приближенного, но единообразного представления. К таким представлениям относятся различные ряды, сходящиеся к значениям функций в окрестности заданной точки. Для разложения функции или выражения ехрr в обычный степенной ряд служат функции series(ехрr, eqn) и series(expr, eqn, n). Здесь ехрr — разлагаемое выражение, eqn — условие (например, в виде х=а) или имя переменной (например, х) и n — необязательное и неотрицательное целое число, задающее число членов ряда (при его отсутствии оно по умолчанию берется равным 6, но может переустанавливаться системной переменной Order). Если в качестве eqn задано имя переменной, то это соответствует разложению по этой переменной в области точки с ее нулевым значением. Задав eqn в виде х=х0, можно получить разложение по переменной х в окрестности точки х = х0.
Разложение получается в форме степенного многочлена, коэффициенты которого задаются рациональными числами. Остаточная погрешность задается членом вида 0(х)^n. При точном разложении этот член отсутствует. В общем случае для его удаления можно использовать функцию convert. Ниже представлены примеры разложения различных выражений в ряд:
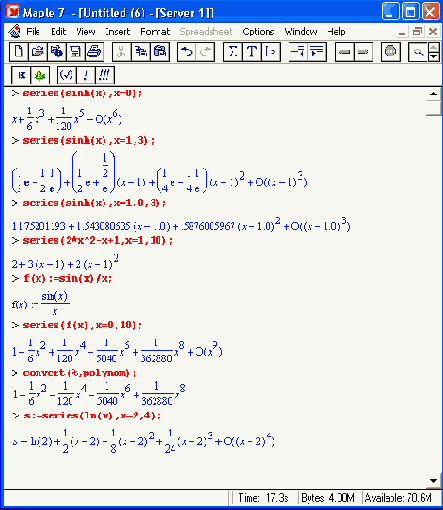
Здесь видно, что член, обозначающий погрешность, отсутствует в тех разложениях, которые точны, например, в разложениях степенных многочленов. Для визуализации приближения рядами заданных аналитических зависимостей очень полезно построить на одном графике кривые аналитической зависимости и разложения в ряд. Мы это покажем чуть позже на примере ряда Тейлора.