Для решения систем линейных уравнений

Для решения систем линейных уравнений созданы мощные матричные методы, которые будут описаны отдельно. Однако функция solve также может с успехом решать системы линейных уравнений. Такое решение в силу простоты записи функции может быть предпочтительным. Для решения система уравнений и перечень неизвестных задаются в виде множеств (см. приведенные ниже примеры).
Рисунок 8.12 дает два примера решения систем из двух линейных уравнений. В первом примере функция solve возвращает решение в виде значений неизвестных х и у, а во втором отказывается это делать.
В чем дело? Оказывается, в том, что во втором случае система просто не имеет решения. Импликативная графика пакета расширения plots дает прекрасную возможность проиллюстрировать решение. Так, нетрудно заметить, что в первом случае геометрическая трактовка решения сводится к нахождению точки пересечения двух прямых, отображающих два уравнения. При этом имеется единственное решение, дающее значения х и у.

Рис. 8.12. Примеры решения системы из двух линейных уравнений с графической иллюстрацией
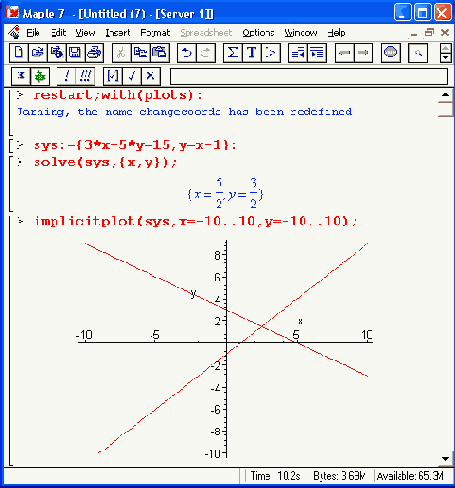
Во втором случае решения и впрямь нет, ибо уравнения задают параллельно расположенные прямые, которые никогда не пересекаются. Рекомендуем читателю самостоятельно проверить и третий случай — бесконечного множества решений. Он имеет место, если оба уравнения описывают одну и ту же зависимость и их графики сливаются в одну прямую.
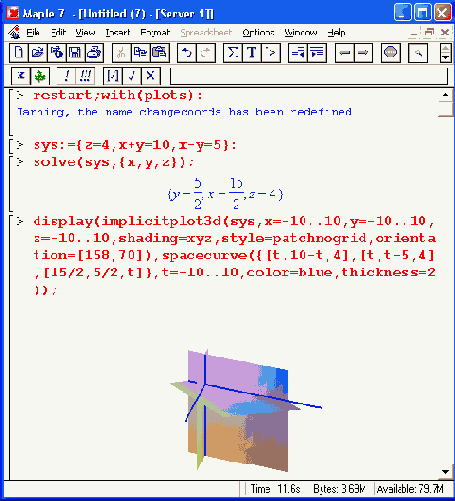
Решение систем из трех линейных уравнений также имеет наглядную геометрическую интерпретацию — в виде точки, в которой пересекаются три плоскости, каждая из которых описывается функцией двух переменных. Для наглядности желательно представить и линии пересечения плоскостей. Это позволяет сделать функция импликативной трехмерной графики tmplicitplotSd, что и показано на рис. 8.13. Для объединения графиков площадей использована функция display.
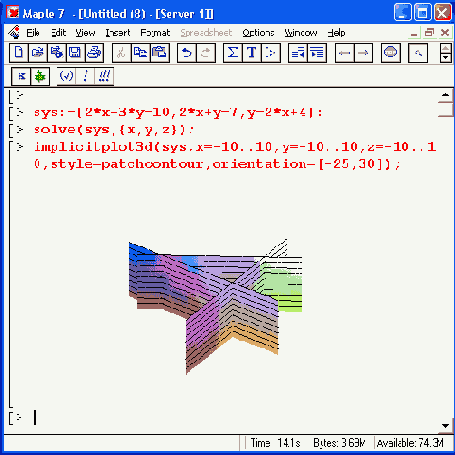
Некоторые проблемы с решением систем из трех линейных уравнений иллюстрируют примеры, приведенные на рис. 8.14, В первом примере решения вообще нет. График показывает, в чем дело, — линии пересечения плоскостей идут параллельно и нигде не пересекаются.
Во втором примере все три плоскости пересекаются по одной линии.

Рис. 8.13. Пример решения системы из трех линейных уравнений с графической иллюстрацией решения

Рис. 8.14. Графическая иллюстрация особых случаев решения системы из трех линейных уравнений
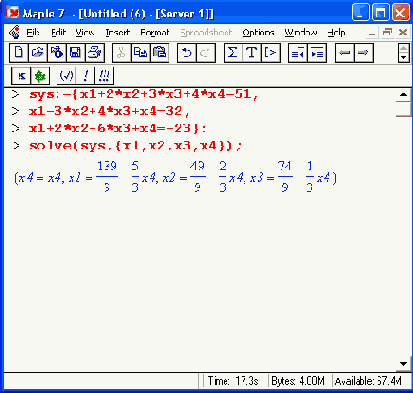
Следующий пример показывает решение системы из четырех линейных уравнений:

Эта система имеет решение, но его простая графическая иллюстрация уже невозможна.
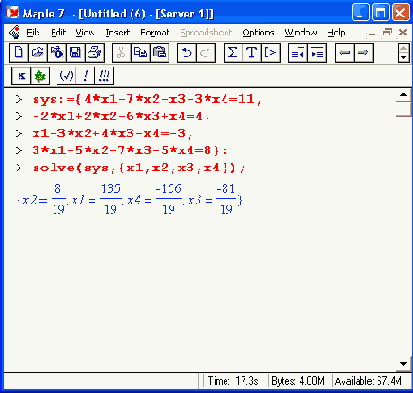
Случай решения неполной системы уравнений (уравнений — 3, а неизвестных — 4) иллюстрирует следующий пример:

Как видно из приведенных примеров, функция solve неплохо справляется с решением систем линейных уравнений.

Содержание раздела