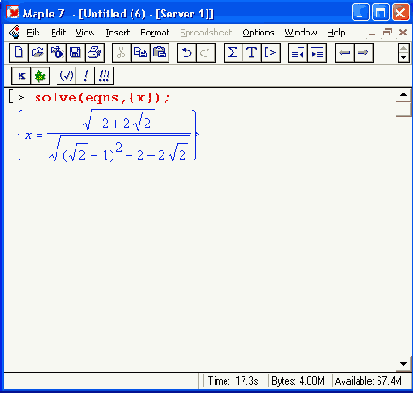
Иллюстрированный самоучитель по Maple
Решение тригонометрических уравнений
Функция solve может использоваться для решения тригонометрических уравнений:
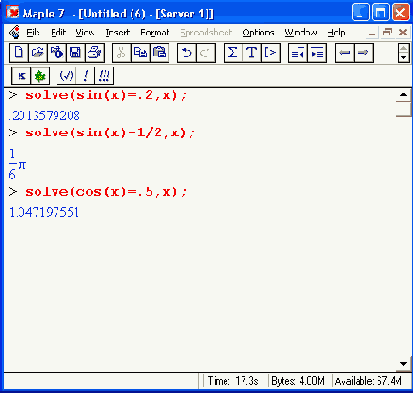
Однако из приведенных примеров видно, что при этом найдено только одно (главное) решение. Периодичность тригонометрических функций и связанная с этим множественность решений оказались проигнорированы. Однако можно попытаться найти все периодические решения, выполнив следующую команду:
> _EnvAllSolutions:=true;
EnvAllSolutions := true
Указанная в ней системная переменная отвечает за поиск всех периодических решений, когда ее значение равно true, и дает поиск только главных решений при значении false, принятом по умолчанию. Так что теперь можно получить следующее:
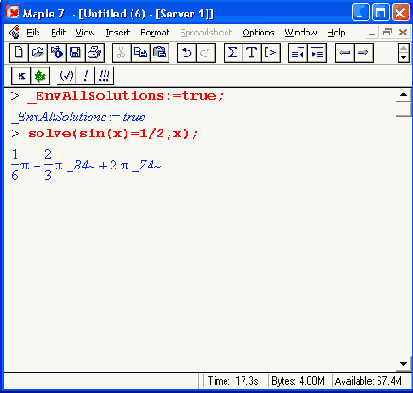
На рис. 8.11 показан более сложный случай решения нелинейного уравнения вида f1(x)=f2(x). где f1(х) = sin(x) и f2(x) = cos(x) - 1. Решение дано в графическом виде и в аналитическом для двух случаев — нахождения главных значений корней и нахождения всех корней.
В решениях встречаются переменные _В1- и _Z1~, означающие ряд натуральных чисел. Благодаря этому через них можно представить периодически повторяющиеся решения.
Примеры решения уравнений с обратными тригонометрическими функциями показаны ниже:
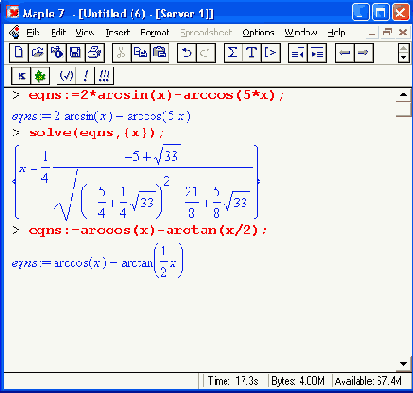
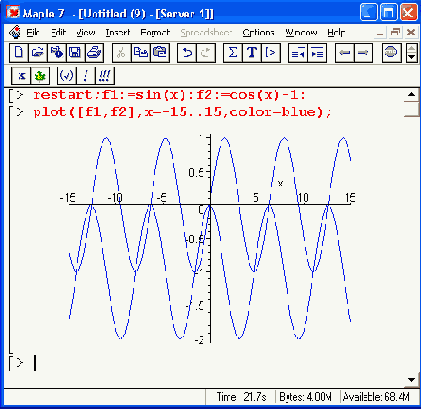
Рис. 8.11. Пример решения уравнения, имеющего периодические решения